Представление графа в программе Пусть дан смешанный граф

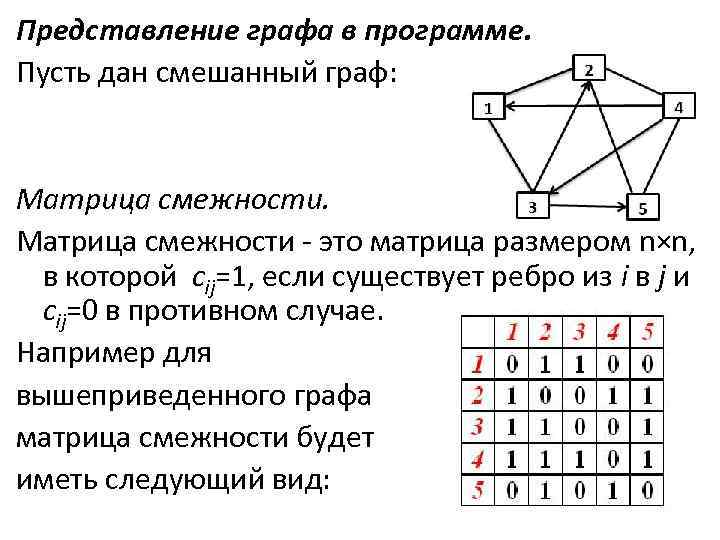Представление графа в программе. Пусть дан смешанный граф: Матрица смежности - это матрица размером n×n, в которой cij=1, если существует ребро из i в j и cij=0 в противном случае. Например для вышеприведенного графа матрица смежности будет иметь следующий вид:

Для неориентированного графа справедливо cij=cji и матрица смежности симметрична. Представление в виде матрицы смежностей удобно для тех алгоритмов на графах, которым часто нужно знать, есть ли в графе данное ребро, ибо время, необходимое для определения наличия ребра, фиксировано. Матрица может быть представлена двумерным массивом или ортогональным списком. Представление ортогональным списком, например, удобно для решения задачи коммивояжера методом ветвей и границ, так как там требуется выполнять удаление строк и столбцов.

В тех случаях, когда ребра имеют веса (например, роль веса играет расстояние между вершинами или стоимость перемещения из вершины в вершину), элементы матрицы смежности – веса рёбер. Признаком отсутствия ребра в этом случае является не 0, а ∞, что означает бесконечно большое расстояние или стоимость. В качестве значения ∞ в программе можно использовать FLT_MAX для величин типа float и DBL_MAX для double, определённые в float. h.

Данные, хранимые в матрице смежности, могут быть представлены также массивом структур, содержащим списки смежности, вида: struct VERSHINA { int nr; // число вершин, смежных с данных int *sm; // массив номеров вершин, смежных с данной }; Массив можно заменить линейным списком.

Полное описание графа для случая, когда вершины и ребра обладают дополнительными свойствами, может быть представлено, например, следующими структурами: struct REBRO{ int w; // номер смежной вершины <свойства ребра>; }; struct VERSHINA{ <свойства вершины>; int nr; // число вершин, смежных данной (число ребер) REBRO *Rebro; // массив рёбер }; struct GRAPH{ int nv; // число вершин VERSHINA *v; // массив вершин }; Массивы могут быть заменены на списки.

Матрица инцидентности — одна из форм представления графа, в которой указываются связи между инцидентными элементами графа (ребро и вершина). Столбцы матрицы соответствуют ребрам, строки — вершинам. Ненулевое значение в ячейке матрицы указывает связь между вершиной и ребром (их инцидентность). В случае ориентированного графа каждому ребру ставится в соответствие "-1" на позиции (x, y) и "1" на позиции (y, x); если связи между вершинами нет, то ставится в соответствие "0".

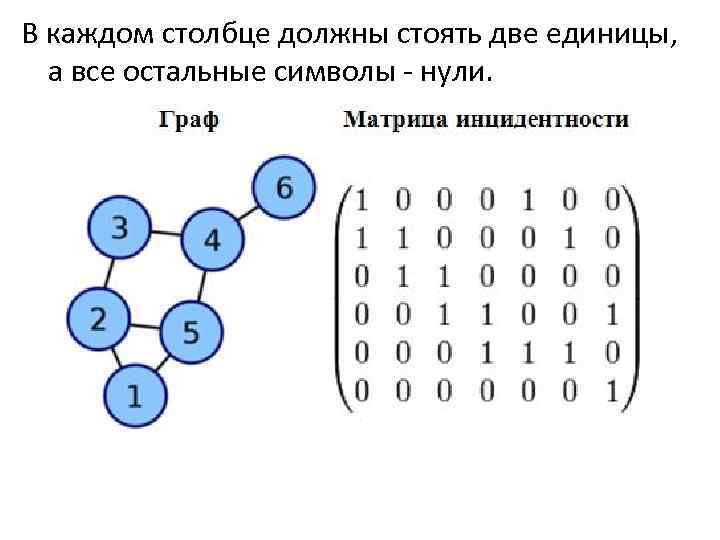В каждом столбце должны стоять две единицы, а все остальные символы - нули.

Массив ребер. Массив ребер – это массив, в котором ребра хранятся парами вершин, которые они соединяют. Это наиболее понятный, но достаточно неудобный способ хранения графа. Однако у него есть один большой плюс - при таком способе представления легко вводить дополнительные характеристики ребер. Для этих целей в структуру, содержащую описание ребра могут быть добавлены дополнительные элементы, например: struct REBRO{ int v, w; // вершины float Weight; // вес ребра };

Для представления конечного автомата структура могла бы иметь вид: struct REBRO{ int v, w; // состояния автомата int Symbol; // входной символ void (*f)(); // функция, выполняемая на переходе из v в w }; Для не ориентированного графа можно при наличии описания ребра (v, w) не включать описание (w, v);

Обход графа в глубину Пусть задан граф G = (V, E), где V — множество вершин графа, E — множество ребер графа. Предположим, что в начальный момент времени все вершины графа окрашены в белый цвет. Выполним следующие действия: 1) Из множества всех белых вершин выберем любую вершину, обозначим её v 1. 2) Выполняем для неё процедуру DFS(v 1). 3) Перекрашиваем её в чёрный цвет. 4) Повторяем шаги 1 -3 до тех пор, пока множество белых вершин не пусто. Процедура DFS (параметр — вершина ) Перекрашиваем вершину u в серый цвет. Для всякой вершины w, смежной с вершиной u, выполняем следующие два шага: – Если вершина w окрашена в белый цвет, выполняем процедуру DFS(w). – Окрашиваем w в чёрный цвет. См демо

Обход графа в ширину Работа всякого алгоритма обхода состоит в последовательном посещении вершин и исследовании ребер. Какие именно действия выполняются при посещении вершины и исследовании ребра - зависит от конкретной задачи, для решения которой производится обход. В любом случае, однако, факт посещения вершины запоминается, так что с момента посещения и до конца работы алгоритма она считается посещенной. Вершину, которая еще не посещена, будем называть новой. В результате посещения вершина становится открытой и остается такой, пока не будут исследованы все инцидентные ей ребра. После этого она превращается в закрытую.

Идея поиска в ширину состоит в том, чтобы посещать вершины в порядке их удаленности от некоторой заранее выбранной или указанной стартовой вершины α. Иначе говоря, сначала посещается сама вершина α, затем все вершины, смежные с α, то есть находящиеся от нее на расстоянии 1, затем вершины, находящиеся от α на расстоянии 2, и т. д. Основная особенность поиска в ширину, отличающая его от других способов обхода графов, состоит в том, что в качестве активной вершины выбирается та из открытых, которая была посещена раньше других. Именно этим обеспечивается главное свойство поиска в ширину: чем ближе вершина к старту, тем раньше она будет посещена.

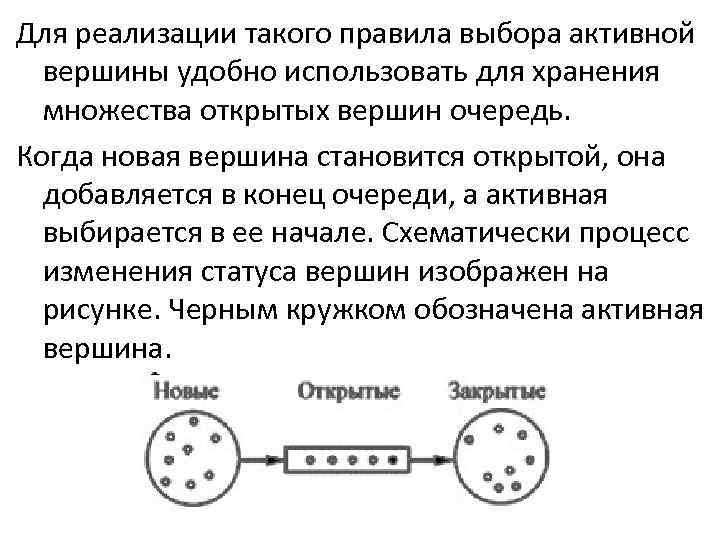Для реализации такого правила выбора активной вершины удобно использовать для хранения множества открытых вершин очередь. Когда новая вершина становится открытой, она добавляется в конец очереди, а активная выбирается в ее начале. Схематически процесс изменения статуса вершин изображен на рисунке. Черным кружком обозначена активная вершина.

Алгоритм обхода в ширину создадим пустую очередь открытых вершин; пометим все вершины как "новые"; while(очередь не пуста) { v=вершина в начале очереди; для всех вершин, смежных с v { v 1=очередная вершина, смежная с v; if(вершина v 1 "новая"){ поместим её в очередь и пометим как открытую; запомним ребро (v, v 1) в массиве пройденных ребер } } // конец прохода вершин смежных с v вершина v становится закрытой и удаляется из очереди; занесем вершину v в массив посещенных вершин; } // конец цикла "пока очередь не пуста"

Если компонента связности единственная в графе, то пройденные ребра образуют остовное дерево. Если граф состоит из более чем одной компоненты связности, то следует повторить процесс для каждой стартовой вершины, оставшейся “новой” после предыдущего прохода алгоритма. В результате будет получен остовный лес.

Поиск кратчайших путей. (Алгоритм Дейкстры) Алгоритм Де йкстры — алгоритм на графах изобретенный нидерландским ученым Э. Дейкстрой в 1959 году. Находит кратчайшее расстояние от одной из вершин графа до всех остальных. Алгоритм работает только для графов без рёбер отрицательного веса. Пусть граф задан вершинами и ребрами. Каждому ребру i j приписан вес (стоимость), равная C[i][j];

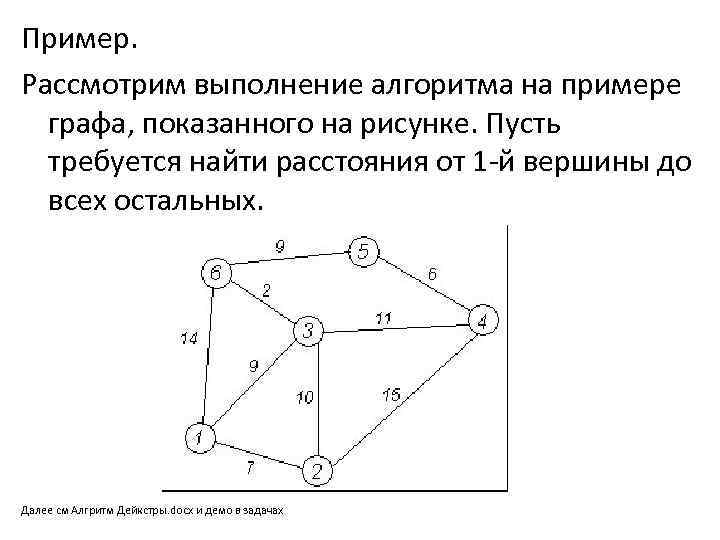Пример. Рассмотрим выполнение алгоритма на примере графа, показанного на рисунке. Пусть требуется найти расстояния от 1 -й вершины до всех остальных. Далее см Алгритм Дейкстры. docx и демо в задачах

Алгоритм Прима Формулировка задачи. Дан взвешенный граф, в котором веса присвоены ребрам. Необходимо найти минимальное остовное дерево имеющую своим корнем одну из вершин графа. Идея алгоритма. Пусть часть остовного дерева уже построена. Это утверждения всегда верно, так как в начале процесса вершина с которой начинается построение уже входит в дерево. Итак если часть остовного дерева уже есть, то множество вершин графа можно разделить на два подмножества: подмножество состоящее из вершин уже построенного остовного дерева и оставшихся вершин графа. Очевидно, что среди ребер соединяющихся эти два множества существует ребро наименьшего веса. Можно доказать, (но мы здесь этого делать не будем) что минимальное дерево проходит через это ребро.

Алгоритм. Множество остовных вершин – исходная вершина. Множество оставшихся - все вершины за исключением исходной. Пока множество оставшихся не пусто { Ищем ребро соединяющее множество остовных и множество оставшихся и имеющее наименьший вес. Для найденного ребра, вершину принадлежащую множеству оставшихся: Вычеркиваем из множества оставшихся. Добавляем к множеству остовных. } См демо

Алгоритм Краскала Формулировка задачи. Дан взвешенный граф, в котором веса присвоены ребрам. Необходимо найти минимальное остовное дерево имеющую своим корнем одну из вершин графа. • Идея алгоритма. Искомые ребра соединяют вершины. Поэтому возможны две стратегии построения. • Можно идти от вершин и для каждой из них искать минимальное ребро (как это сделано в алгоритме Прима) • Можно для каждого ребра выяснять можно ли его включить в строящееся дерево (алгоритм Краскала).

Во-первых, ребра графа пронумеровываем в порядке возрастания весов. Затем для каждого ребра начиная с первого проверяем соединяет или нет оно две несвязные вершины, если да, то его можно включить в остовное дерево. Ясно, что если мы имеем V вершин, то работа алгоритма начинается с V несвязных компонент графа (в начале из графа все ребра исключаем). Для того, чтобы их связать необходимо найти V-1 ребро. Другими словами, алгоритм организует процесс роста компонент связности в процессе которого он объединяются друг с другом до тех пор пока не останется одна являющаяся конечным результатом.

Алгоритм 1. Создаем список ребер по возрастанию веса. 2. Создаем множество компонент связности каждая из которых содержит ровно одну вершину. 3. Пока компонент связности больше чем одна. 3. 1 Взять ребро из начала списка ребер. 3. 2 Если ребро соединяет две разных компоненты связности то 3. 2. 1 Компоненты связности объединить в одну. См демо