Представление числовой информации в ЭВМ 1 Код

Представление числовой информации в ЭВМ

1. Код Грея, Смешенный код 2. Представление вещественных чисел 3. Погрешность представления числовой информации ЭВМ

1. Код Грея, Смешенный код Смешанный код, или, как его еще называют, двоичный код с избытком, используется в ЭВМ для упрощения операций над порядками чисел с плавающей запятой.

•

•

Правила перевода числа из кода Грея в обычный двоичный код сводятся к следующему: • Первая единица со стороны старших разрядов остается без изменения. • Последующие цифры (0 и 1) остаются без изменения, если число единиц, им предшествующих, честно, инвертируются – если нечетно.

• Код Грея широко используется для кодирования положений валов, дисков и т. д. , позволяя свести к единице младшего разряда погрешность при считывании. • Основное особенность кода Грея, то что погрешность при считывании не может превосходить единицы младшего разряда.

2. Представление вещественных чисел •

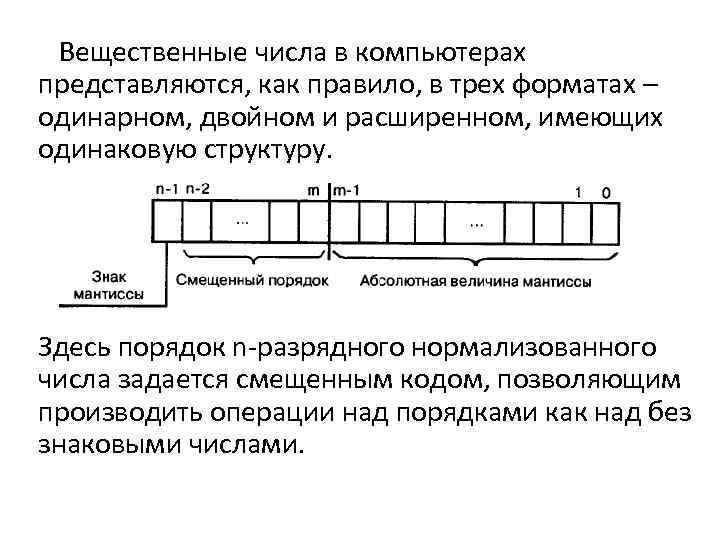Вещественные числа в компьютерах представляются, как правило, в трех форматах – одинарном, двойном и расширенном, имеющих одинаковую структуру. Здесь порядок n-разрядного нормализованного числа задается смещенным кодом, позволяющим производить операции над порядками как над без знаковыми числами.

Чем больше разрядов отводится под запись мантиссы, тем выше точность представления числа. Чем больше разрядов занимает порядок, тем шире диапазон от наименьшего отличного от ноля числа до наибольшего числа, представимого в машине при заданном формате. Нормализованное число двойной точности представляет собой 64 -разрядное нормализованное число со знаком, 11 разрядным смещенным порядком и 53 разрядной мантиссой.

При алгебраическом сложении и вычитании чисел, представленных в формате с плавающей запятой, сначала уравниваются порядки слагаемых. В процессе выравнивания порядков мантисса числа с меньшим порядком сдвигается в своем регистре вправо на количество разрядов, равное разности порядков операндов. После каждого сдвига порядок увеличивается на единицу. В результате выравнивания порядков одноименные разряды чисел оказываются расположенными в соответствующих разрядах обоих регистров, после чего мантиссы складываются или вычитаются.

При делении из порядка делимого вычитается порядок делителя, а над мантиссами совершается обычная операция деления. В случае необходимости полученный результат нормализуется, что приводит к изменению порядков, так каждый сдвиг на один разряд влево соответствует уменьшению порядка на единицу, а сдвиг вправо — увеличению его на единицу.

3. Погрешность представления числовой информации ЭВМ •

•

•

•

•