ПРЕДСТАВЛЕНИЕ ЧИСЕЛ В ПАМЯТИ ЭВМ Формы представления

ПРЕДСТАВЛЕНИЕ ЧИСЕЛ В ПАМЯТИ ЭВМ

Формы представления чисел n n Естественная Экспоненциальная

ПРЕДСТАВЛЕНИЕ ЦЕЛЫХ ЧИСЕЛ В ЭВМ Любая информация в ЭВМ представляется в виде двоичных кодов. • Отдельные элементы двоичного кода, принимающие значение 0 или 1, называют разрядами или битами. • Память компьютера условно делиться на отсеки или ячейки, каждая из которых имеет свой номер. Нумерация начинается с нуля. • Минимальной адресуемой ячейкой памяти называется байт – 8 двоичных разрядов. порядковый номер байта называется его адресом. • Наибольшую последовательность битов, которую процессор может обрабатывать как единое целое, называют машинным словом. 3

ПРЕДСТАВЛЕНИЕ ЦЕЛЫХ ЧИСЕЛ Длина машинного слова может быть разной - 8 , 16 , 32 бит и т. д. Двоичные разряды в любой ячейке памяти нумеруются справа налево, начиная с нуля. Существуют два основных формата представления чисел в памяти компьютера. 1. для кодирования целых чисел - формат с фиксированной точкой 2. для задания некоторого подмножества действительных чисел - формат с плавающей точкой M*q P 4

ПРЕДСТАВЛЕНИЕ ЦЕЛЫХ ЧИСЕЛ Форматы представления: 1. Знаковый 2. Беззнаковый Под знак отводится старший разряд ячейки: 0 - для положительных чисел, 1 - для отрицательных чисел. Формат = тип переменной 5

Машинные коды Для упрощения реализации арифметических операций в компьютере целые числа представляются специальными кодами - прямым, обратным и дополнительным. Прямой код двоичного числа — это само двоичное число, причем значение знакового разряда для положительных чисел равно 0, а для отрицательных чисел 1. Обратный код отрицательного числа получается из прямого кода путем замены нулей единицами, а единиц нулями, исключая знаковый разряд. Дополнительный код отрицательного числа образуется как результат суммирования обратного кода с единицей младшего разряда. Перенос в знаковый разряд при этом теряется. Примечание. Дополнительный код основан на понятии дополнения числа величины, которую надо добавить к числу, чтобы получить переход единицы в старшем разряде. Дополнением k-разрядного целого числа Z в системе счисления с основанием q называется величина: D = q k – Z Для положительного числа прямой, обратный и дополнительный коды одинаковы. 6

Прямой код двоичного числа образуется из абсолютного значения этого числа и кода знака (0 или 1) перед его старшим числовым разрядом. Пример. А 10 = +10; А 2 = +1010; [А 2]п = 0. 1010 В 10 = – 15; В 2 = – 1111; [В 2]п = 1. 1111

Обратный код n n n Свое название обратный код получил потому, что коды цифр отрицательного числа заменены на инверсные. Наиболее важные свойства обратного кода чисел: сложение положительного числа С с его отрицательным значением в обратном коде дает т. н. машинную единицу МЕок=1|11… 11, состоящую из единиц в знаковом и в значащих разрядах числа; нуль в обратном коде имеет двоякое значение. Он может быть как положительным числом – 0|00… 00, так и отрицательным 1|11… 11. Значение отрицательного числа совпадает с МЕок. Двойственное представление 0 явилось причиной того, что в современных ЭВМ все числа представляются не обратным, а дополнительным кодом.

Дополнительный код положительных чисел совпадает с их прямым кодом. Дополнительный код отрицательного числа представляет собой результат суммирования обратного кода числа с единицей младшего разряда (20 – для целых чисел, 2 -л – для дробных) Пример. А 10 = +10; А 2 = +1010; [А 2]дк = [А 2]ок = [А 2]п = 0. 1010 В 10 = – 15; В 2 = – 1111; [В 2]дк = [В 2]ок + 20 = 1|0000+1 = 1. 0001 Основные свойства дополнительного кода: n сложение дополнительного кода положительного числа с его отрицательным значением дает т. н. машинную единицу дополнительного кода: МЕдк= МЕок + 20 = 10. 00… 00, т. е. число 10 (два) в знаковых разрядах числа; n дополнительный код называется так потому, что представление отрицательных чисел является дополнением прямого кода чисел до машинной единицы МЕдк.

Пример 1. Определить прямой, обратный и дополнительный коды следующих двоичных чисел: а)100100; б) -100011; в) -100100. Решение Будем считать, что число размещается в двух байтах. Старший бит – знак разряда. Незначащие нули добавляются слева от числа. Результат представим в виде таблицы: Число Прямой код Обратный код Дополнительны й код 100100 0000000000100100 -100011 100000100011 11111011100 11111011101 -100100 100000100100 11111011011 11111011100 10

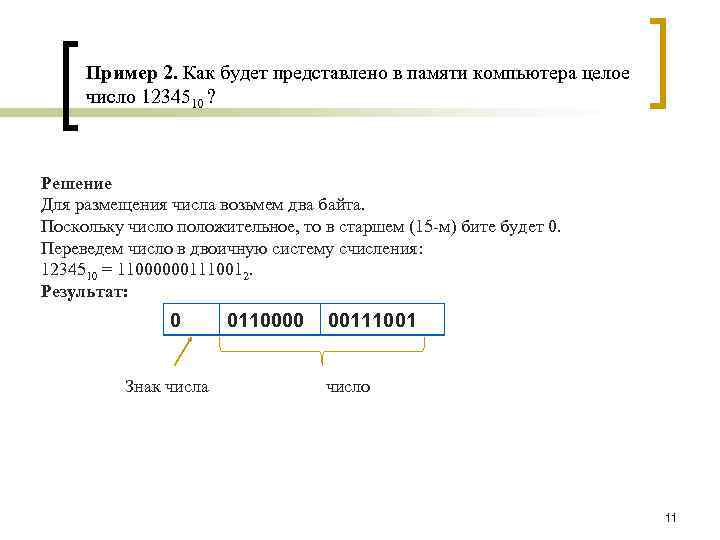Пример 2. Как будет представлено в памяти компьютера целое число 1234510 ? Решение Для размещения числа возьмем два байта. Поскольку число положительное, то в старшем (15 -м) бите будет 0. Переведем число в двоичную систему счисления: 1234510 = 110000001110012. Результат: 0 Знак числа 0110000 00111001 число 11

Задания для самостоятельного выполнения 1. Запишите прямые коды десятичных чисел в однобайтовом формате: а) 64 б) 58 в) 72 г) -96 2. Запишите двоичные числа в дополнительном коде: а) 1010 б) -1001 в) -11 г) -11011 3. Переведите в прямой код числа, записанные в дополнительном коде, и найдите их десятичные эквиваленты: а) 00000100 б) 11111001 4. Представьте целые числа в 16 -разрядной ЭВМ: а) 25 б) -25 в) 801 г) -610 12

ЦЕЛОЧИСЛЕННАЯ ДВОИЧНАЯ АРИФМЕТИКА В ЭВМ 13

Сложение чисел производится в дополнительных кодах поразрядно. При выполнении арифметических операций число может выйти за указанные границы. Произойдет переполнение разрядной сетки, поэтому при работе с большими целыми числами под них выделяется больше места, например 4 байта. Чтобы избежать ситуации переполнения, в языках программирования предусмотрено строгое описание типа переменной, которым определяется набор возможных ее значений. Вычитание целых чисел эквивалентно сложению с отрицательным числом. Отрицательное число может быть представлено в прямом коде. Однако использование прямого кода усложняет структуру команд процессора. При выполнении сложения чисел с разными знаками требуется выбрать из них большее по модулю, затем вычесть из него меньшее, выяснить знак большего и присвоить этот знак остатку. По этой причине в компьютерах используется представление отрицательного числа в дополнительном коде. Таким образом, операция вычитания выполняется как сложение с дополнительным кодом вычитаемого. 14

Операции умножения и деления выполняются в прямом коде с использованием итерационных алгоритмов (ряда повторяющихся шагов). Умножение двоичных чисел сводится к двум операциям: сложения и сдвига. Операция деления для целых чисел однозначно не определена, поскольку в общем случае приводит к появлению нецелых (вещественных) чисел. Существуют различные методы и алгоритмы реализации этой операции в разных процессорах. 15

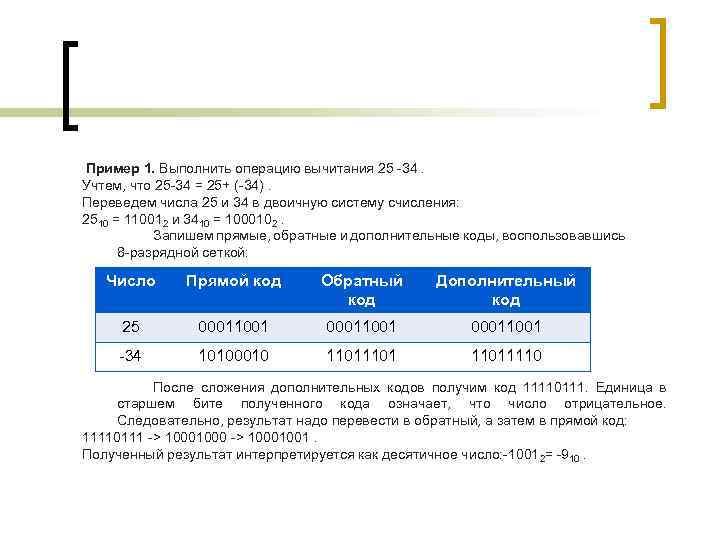Пример 1. Выполнить операцию вычитания 25 -34. Учтем, что 25 -34 = 25+ (-34). Переведем числа 25 и 34 в двоичную систему счисления: 2510 = 110012 и 3410 = 1000102. Запишем прямые, обратные и дополнительные коды, воспользовавшись 8 -разрядной сеткой: Число Прямой код Обратный код Дополнительный код 25 00011001 -34 10100010 11011110 После сложения дополнительных кодов получим код 11110111. Единица в старшем бите полученного кода означает, что число отрицательное. Следовательно, результат надо перевести в обратный, а затем в прямой код: 11110111 -> 10001001. Полученный результат интерпретируется как десятичное число: -10012= -910.

Операции циклического сдвига Операции shl и shr, сдвигают последовательность битов на заданное число позиций влево или вправо соответственно. При этом биты, которые выходят за разрядную сетку, теряются. При выполнении операции shl освободившиеся справа биты заполняются нулями. При выполнении операции shr освободившиеся слева биты заполняются единицами при сдвиге вправо отрицательных значений и нулями в случае положительных значений. С помощью операции shl возможна замена операции умножения целых чисел на степени двойки. Следующие пары выражений приводят к одинаковому результату: (a shl 1) = a * 2, (a shl 2) = a * 4, (a shl 3) = a * 8.

var A, B: byte; Begin A : = 11; {00001011} B : = 6; {00000110} writeln('A=', A); writeln('B=', B); writeln('not A = ', not A); {11110100 = 244} writeln('A and B = ', A and B); {00000010 = 2} writeln('A or B = ', A or B); {00001111 = 15} writeln('A xor B = ', A xor B); {00001101 = 13} writeln('A shl 1 = ', A shl 1); {00010110 = 22} writeln('B shr 2 = ', B shr 2); {00000001 = 1} end.

Дополнительно n n https: //ru. wikiversity. org/wiki/Вычислительная_техника_и_программирование/Занятие _4 http: //www. intuit. ru/studies/courses/3481/723/lecture/14242? page=2