Представление чисел в компьютере Числа 1 1 Целые

Представление чисел в компьютере Числа 1. 1 Целые числа. 1. 2 Действительные числа. 1. 3 Примеры 1

Числа 1. 1 Целые числа n Представляются в формате с фиксированной точкой. Число занимает 16 бит в 16 разрядном компьютере, 32 бита — в 32 разрядном. 2

n n n Положительные целые числа Хранятся в прямом коде. Чтобы получить прямой код числа нужно: перевести его в двоичную систему; дополнить результат лидирующими нулями до 16 или 32 разрядов, например: 3

4

n Старший разряд положительного числа равен 0. Максимальное число в такой форме 5

n n Отрицательные целые числа. Хранятся в дополнительном коде: получить внутреннее представление модуля числа; инвертировать его, инверсия 1 0, 0 1; прибавить единицу. 6

Пример, число – 160710. Прямой код модуля n 0000 0110 0100 0111 Инверсия n 1111 1001 1011 1000 Плюс 1 n 1111 1001 1011 1001 n 7

n Старший разряд отрицательного числа равен 1. Минимальное число в 16 -разрядном формате равно -215=-32768. 8

n n 1. 2 Действительные числа Представляют в форме с плавающей запятой: здесь m — мантисса числа, p — основание системы, n — порядок, например 9

n n В компьютерах используют различные варианты форматов чисел. Для примера рассмотрим форматы представления чисел сопроцессора 8087. 10

n n 1. 3 Примеры Целые числа. Записываются в дополнительном двоичном коде. Заметим, что дополнительный двоичный код положительного числа совпадает с его прямым кодом. 11

Целое слово (-32768 до 32767) 15 0 Короткое целое слово или двойное слово (-232 до 232) 31 0 Длинное слово, 4 слова (-264 до 264 – 1) 63 12

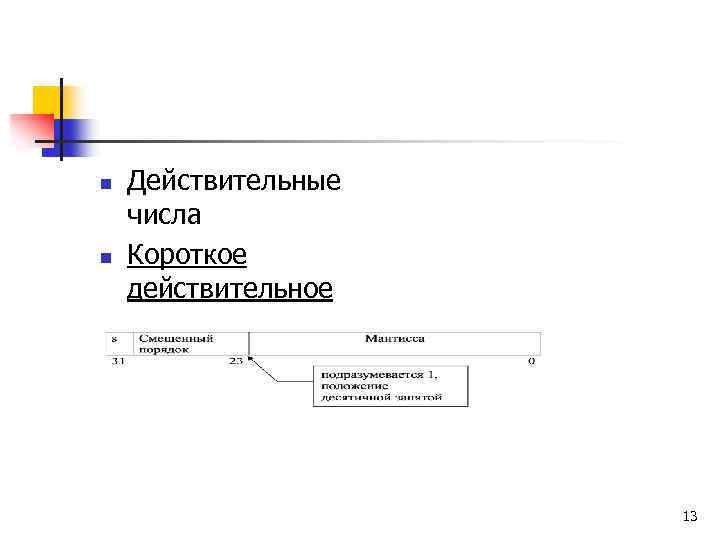n n Действительные числа Короткое действительное 13

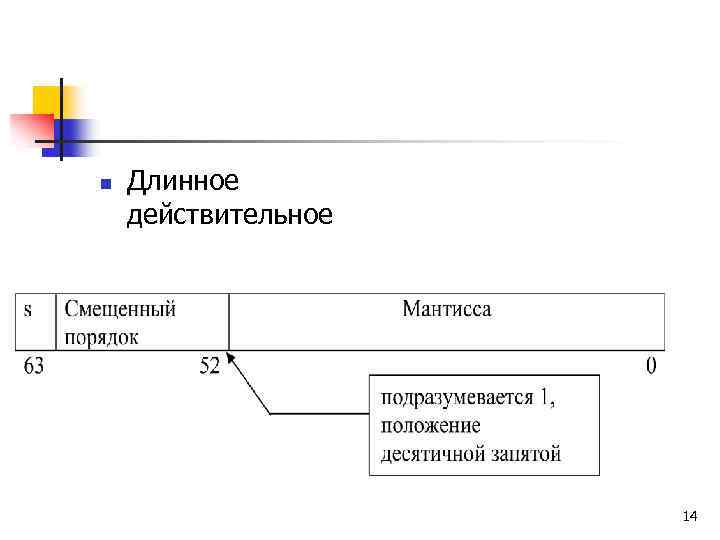n Длинное действительное 14

n Временное действительное 15

n Временное действительное, используется для промежуточных результатов вычислений внутри сопроцессора, чтобы обеспечить большую точность. Остальные форматы используют для записи и чтения чисел в память, т. е. вне сопроцессора. 16

n Мы водим, что место, отводимое для числа с плавающей точкой, делится на 3 поля: знак числа, смещенный порядок, мантисса. 17

n Мантисса. Используется нормализованная мантисса: 18

n Мантисса записывается в прямом коде. Количество цифр мантиссы определяет точность представления числа (число 1, 234 более точное число, чем число 1, 2). Мантисса, содержащая 23 бита, дает 6 -7 десятичных цифр по точности. 19

n Смещенный порядок. К порядку прибавляется смещение так, чтобы минимальный отрицательный порядок стал нулевым. Знак у порядка не запоминается. Короткое действительное число смещается константой 12710=0111 11112, длинное действительное — 102310, временное действительное — 1638310. 20

n Количество цифр порядка определяет диапазон чисел. Например, в формате длинного действительного числа имеем 11 -битовы порядок, что дает диапазон чисел от 2 -1023 21023 , или в десятичной форме соответствует диапазону 10 -307 до 10307. 21

n Для примера рассмотрим представление числа 25, 324 в форме короткого действительного числа. n Переведем модуль числа в двоичную систему счисления с 24 значащими цифрами: 11001, 0101000101011000000. n n n Нормализуем мантиссу: 1, 10010101000101011000000 24 (здесь мантисса в двоичном представлении, а порядок — в десятичном). Прибавим к порядку смещение и переведем его в двоичную систему: 4+127=13110=100000112. Учтем знак числа (0 — для положительных чисел, 1 – для отрицательных), запишем формат числа: 22

Вопросы n n В каком формате представляют целые числа? Как получить прямой код числа? Как получить дополнительный код положительного числа? Как получить дополнительный код отрицательного числа? 23

n n n В каком формате хранят действительные числа? Приведите выражение и пример. Назовите форматы действительных чисел. Приведите пример кода короткого действительного числа. 24

n n n Что такое смещенный порядок? Хранится ли знак действительного числа? Хранится ли знак порядка действительного числа? 25