Предмет теоретической механики Основные понятия теоретической механики

Предмет теоретической механики. Основные понятия теоретической механики

Теоретическая механика есть наука о законах движения материальных тел и их взаимодействии. Под движением понимается изменение положения материальных тел относительно друга с течением времени. Под взаимодействием в механике (механическим взаимодействием) понимается способность или предрасположенность материальных тел изменять свое положения относительно друга с течением времени. Объектами теоретической механики являются: • материальная точка; • система материальных точек; • твёрдое тело; • система твёрдых тел.

Под материальной точкой в теоретической механике понимается материальное тело имеющее массу, размерами которого, при изучении механических движений, можно пренебречь. Очевидно, материальная точка есть материальное тело лишённое размеров, но имеющее массу, а значит имеет способность к механическому взаимодействию обусловленному этой массой. Система материальных точек есть совокупность точек обуславливающих как движение друга, так и механическое взаимодействие между собой. Твердое тело (абсолютно твёрдое тело) в теоретической механике есть совокупность материальных точек, для которых расстояния между любыми двумя точками есть величина неизменная. Система твердых тел есть совокупность твердых тел обуславливающих как движение друга, так и механическое взаимодействие между собой. Механической системой называют совокупность её объектов, материальных точек или твёрдых тел. Очевидно, положение и движение каждого объекта системы зависят от положения и движения других объетов этой системы.

Состояние равновесия или движения данного тела зависит от характера его механических взаимодействий с другими телами, т. е. от тех давлений, притяжений или отталкиваний, которые тело испытывает в результате этих взаимодействий. Величина, являющаяся основной мерой механического взаимодействия материальных тел, называется в механике силой. Сила в теоретической механике есть мера механического взаимодействия, определяющая ее интенсивность и направление. Рассматриваемые в механике величины можно разделить на скалярные, т. е. такие, которые полностью характеризуются их числовым значением, и векторные, т. е. такие, которые помимо числового значения характеризуются еще и направлением в пространстве. Сила — величина векторная, её действие на тело определяется: 1) числовым значением или модулем силы, 2) направлением силы, 3) точкой приложения силы. Прямая вдоль которой направлена сила называется линией действия силы

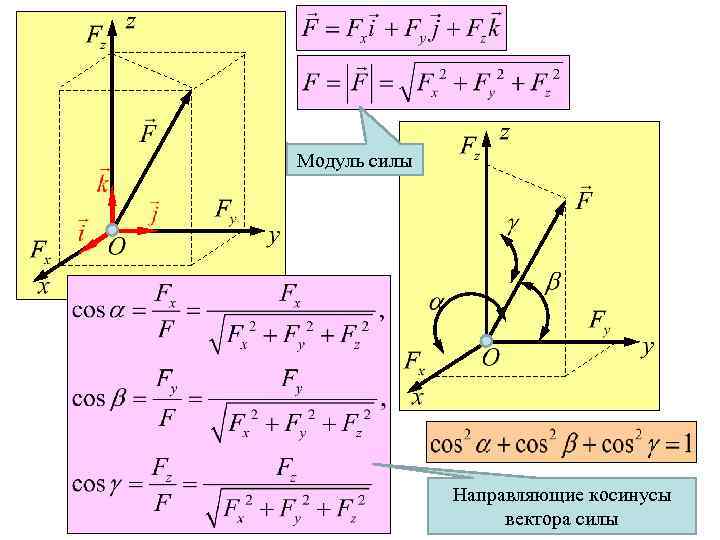Модуль силы Направляющие косинусы вектора силы

Системой сил называют совокупность сил, действующих на рассматриваемое тело или в более общем случае — на точки механической системы. Можно рассматривать систему сил, приложенных к одной материальной точке. Если линии действия всех сил лежат в одной плоскости, система сил называется плоской, а если эти линии действия не лежат в одной плоскости, то пространственной. Силы, линии действия которых пересекаются в одной точке, называются сходящимися, а силы, линии действия которых параллельны другу, — параллельными. Тело, которому из данного положения можно сообщить любое перемещение в пространстве, т. е. его положение в пространстве не ограничено, называется свободным.

Если одну систему сил, действующих на свободное твердое тело, можно заменить другой системой, не изменяя при этом её механического состояния, т. е. состояния покоя или движения, в котором находится тело, то такие две системы сил называются эквивалентными. Очевидно, две системы сил эквивалентны между собой, если их действие по отдельности на одно и то же твердое тело или материальную точку одинаково при прочих равных условиях, т. е. если одна система сил приводит твердое тело или материальную точку в какое-то движение, например, из состояния покоя, то другая система сил, эквивалентная первой, сообщит такое же движение.

Движения, вызванные действием эквивалентных систем сил, имеют одинаковые характеристики для каждого момента времени. Условие эквивалентности двух систем сил имеет вид и

Равновесной системой сил (уравновешенной или системой сил эквивалентной нулю ), называют такую систему сил, действие которой на твердое тело или материальную точку, находящиеся в покое или движущиеся по инерции, не приводит к изменению состояния покоя или движения по инерции этого тела или материальной точки. Равновесная (уравновешенная) система сил Если данная система сил эквивалентна одной силе, то эта сила называется равнодействующей данной системы сил. Равнодействующая Очевидно, действие равнодействующей силы системы сил на твердое тело или материальную точку эквивалентно действию этой системы сил. Сила, равная равнодействующей по модулю, прямо противоположная ей по направлению и действующая вдоль той же прямой, называется уравновешивающей силой.

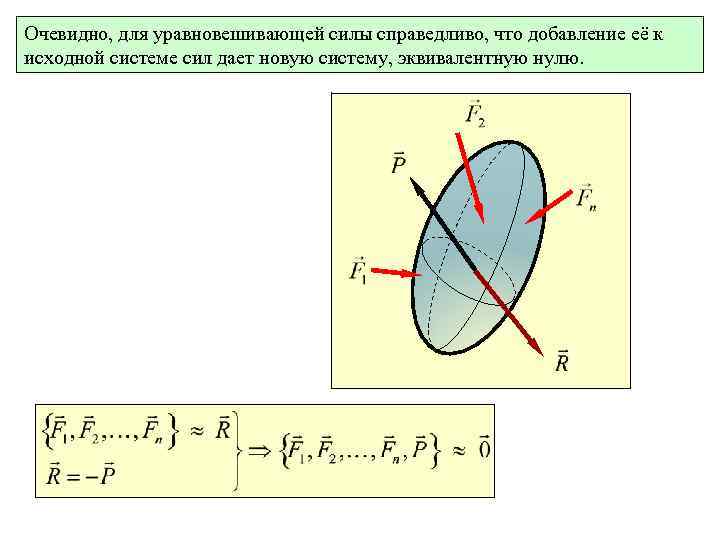Очевидно, для уравновешивающей силы справедливо, что добавление её к исходной системе сил дает новую систему, эквивалентную нулю.

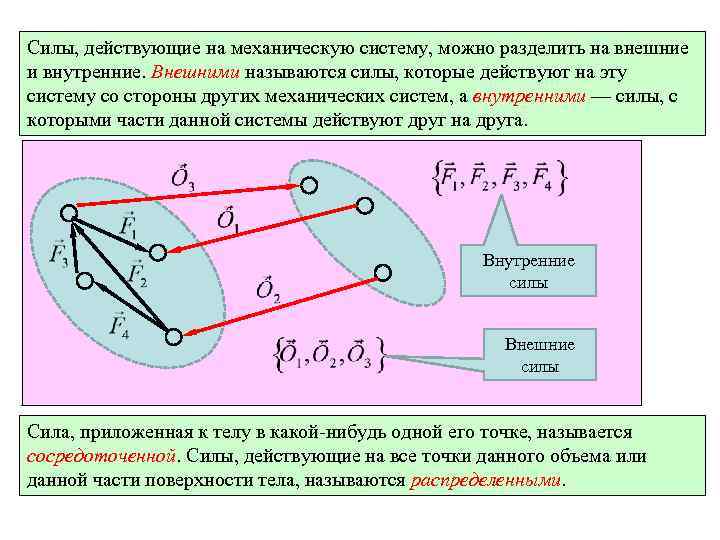Силы, действующие на механическую систему, можно разделить на внешние и внутренние. Внешними называются силы, которые действуют на эту систему со стороны других механических систем, а внутренними — силы, с которыми части данной системы действуют друг на друга. Внутренние силы Внешние силы Сила, приложенная к телу в какой-нибудь одной его точке, называется сосредоточенной. Силы, действующие на все точки данного объема или данной части поверхности тела, называются распределенными.

По характеру решаемых задач теоретическая механика делится на три раздела статику, кинематику и динамику. Статикой называется раздел механики, в котором излагается общее учение о силах и изучаются условия равновесия материальных тел, находящихся под действием сил. Под равновесием понимается состояние покоя тела по отношению к другим телам, т. е. отсутствие движение его относительно этих тел. Условия равновесия тела существенно зависят от того, является ли это тело твердым, жидким или газообразным. Равновесие жидких и газообразных тел изучается в курсам гидростатики или аэростатики. В теоретической механики рассматриваются как правило только задачи о равновесии твёрдых тел. Кинематикой называется раздел механики, в котором изучается движение материальных тел в пространстве с геометрической точки зрения, вне связи с силами, определяющими это движение. Т. е. изучаются геометрические свойства траектории, скорости и ускорения движения. Динамикой называется раздел механики, в котором изучается движение материальных тел в пространстве в зависимости от действующих на них сил.

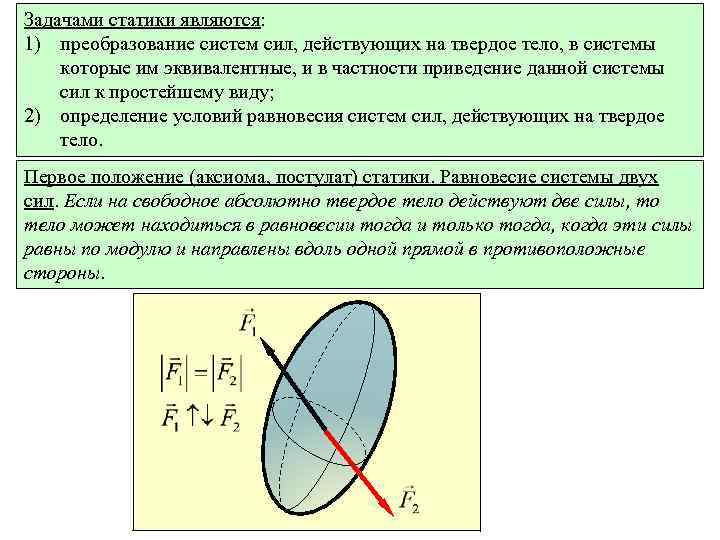Задачами статики являются: 1) преобразование систем сил, действующих на твердое тело, в системы которые им эквивалентные, и в частности приведение данной системы сил к простейшему виду; 2) определение условий равновесия систем сил, действующих на твердое тело. Первое положение (аксиома, постулат) статики. Равновесие системы двух сил. Если на свободное абсолютно твердое тело действуют две силы, то тело может находиться в равновесии тогда и только тогда, когда эти силы равны по модулю и направлены вдоль одной прямой в противоположные стороны.

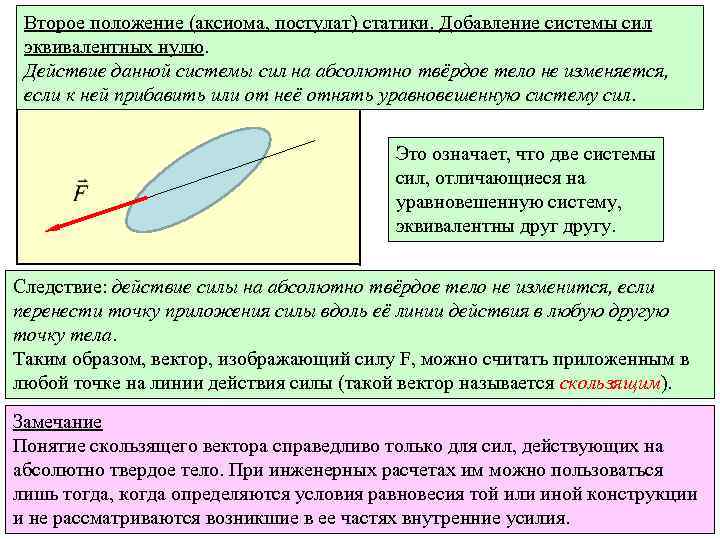Второе положение (аксиома, постулат) статики. Добавление системы сил эквивалентных нулю. Действие данной системы сил на абсолютно твёрдое тело не изменяется, если к ней прибавить или от неё отнять уравновешенную систему сил. Это означает, что две системы сил, отличающиеся на уравновешенную систему, эквивалентны другу. Следствие: действие силы на абсолютно твёрдое тело не изменится, если перенести точку приложения силы вдоль её линии действия в любую другую точку тела. Таким образом, вектор, изображающий силу F, можно считать приложенным в любой точке на линии действия силы (такой вектор называется скользящим). Замечание Понятие скользящего вектора справедливо только для сил, действующих на абсолютно твердое тело. При инженерных расчетах им можно пользоваться лишь тогда, когда определяются условия равновесия той или иной конструкции и не рассматриваются возникшие в ее частях внутренние усилия.

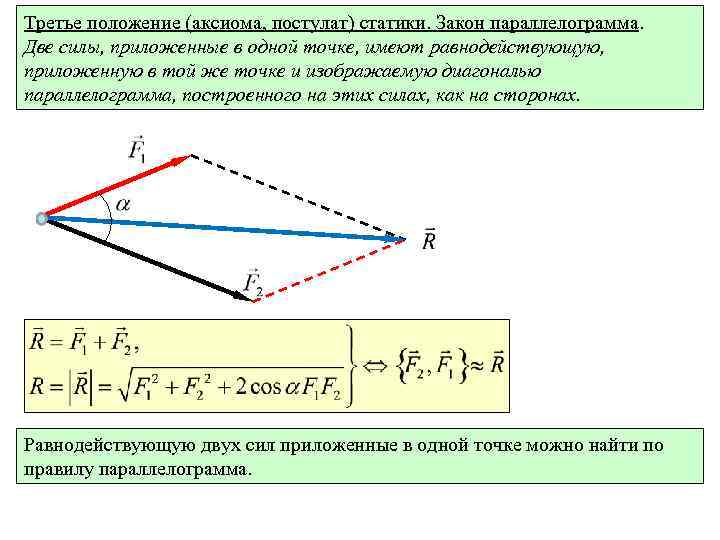Третье положение (аксиома, постулат) статики. Закон параллелограмма. Две силы, приложенные в одной точке, имеют равнодействующую, приложенную в той же точке и изображаемую диагональю параллелограмма, построенного на этих силах, как на сторонах. Равнодействующую двух сил приложенные в одной точке можно найти по правилу параллелограмма.

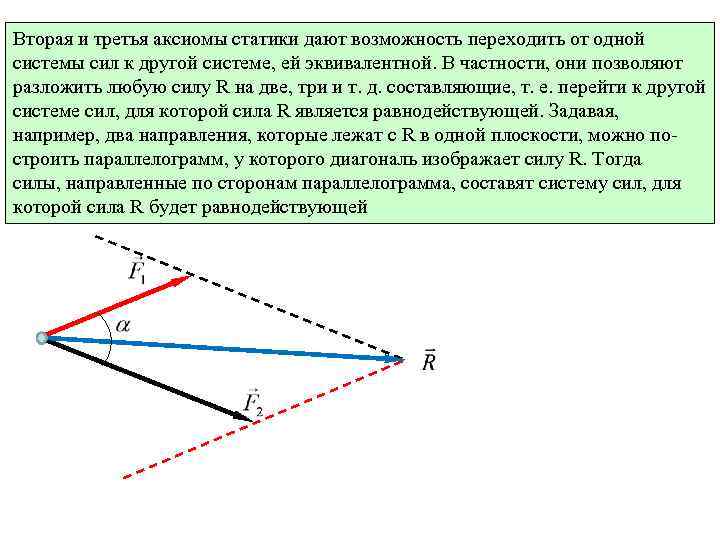Вторая и третья аксиомы статики дают возможность переходить от одной системы сил к другой системе, ей эквивалентной. В частности, они позволяют разложить любую силу R на две, три и т. д. составляющие, т. е. перейти к другой системе сил, для которой сила R является равнодействующей. Задавая, например, два направления, которые лежат с R в одной плоскости, можно построить параллелограмм, у которого диагональ изображает силу R. Тогда силы, направленные по сторонам параллелограмма, составят систему сил, для которой сила R будет равнодействующей