Предмет механики Механика – часть

Предмет механики Механика – часть физики, которая изучает закономерности механического движения и причины, вызывающие или изменяющие это движение. Механическое движение – это изменение с течением времени взаимного расположения тел или их частей. 1

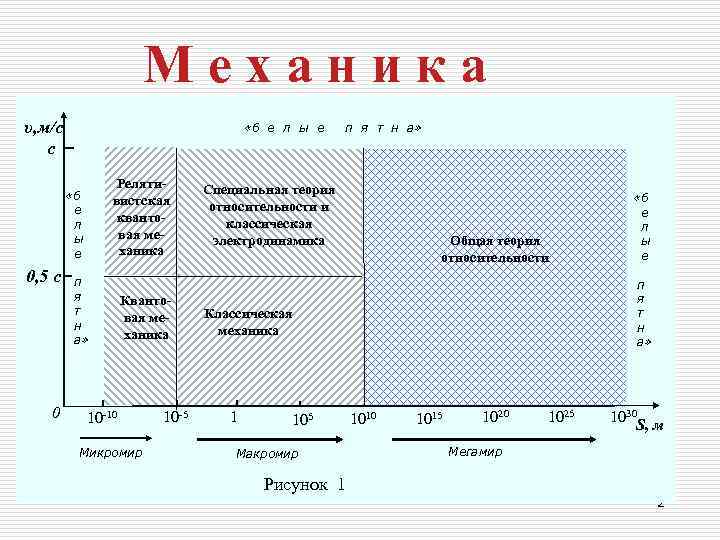
Механика υ, м/с «б е л ы е п я т н а» с υ Реляти- Специальная теория «б вистская «б е относительности и е кванто- классическая л л ы вая ме- электродинамика Общая теория ы е ханика относительности е 0, 5 с п п я Кванто- я т Классическая т вая ме- н механика н а» ханика а» 0 10 -10 10 -5 1 105 1010 1015 1020 1025 1030 S, м Микромир Макромир Мегамир Рисунок 1 2

Классическая механика Кинематика изучает движение тел, не рассматривая причины, которые вызывают или изменяют это движение. Динамика изучает законы движения тел и причины, которые вызывают или изменяют это движение. Статика изучает законы равновесия системы тел. 3

Основные понятия Материальная точка это тело, размерами и формой которого в данной задаче можно пренебречь. Абсолютно твердым телом называется тело, расстояние между любыми точками которого не меняется со временем. Абсолютно твердое тело, с которым связывают ту или иную систему координат, условно считают неподвижным и относительно которого исследуют движение других тел, называется телом отсчета. 4

Система отсчета Совокупность системы координат, жестко связанной с телом отсчета, часов для отсчета времени с указанием начала отсчета времени называется системой отсчета. Радиус-вектор Вектор, проведённый из точки отсчёта к положению r (t) движущегося тела в данный момент времени называется О радиус – вектором. 5

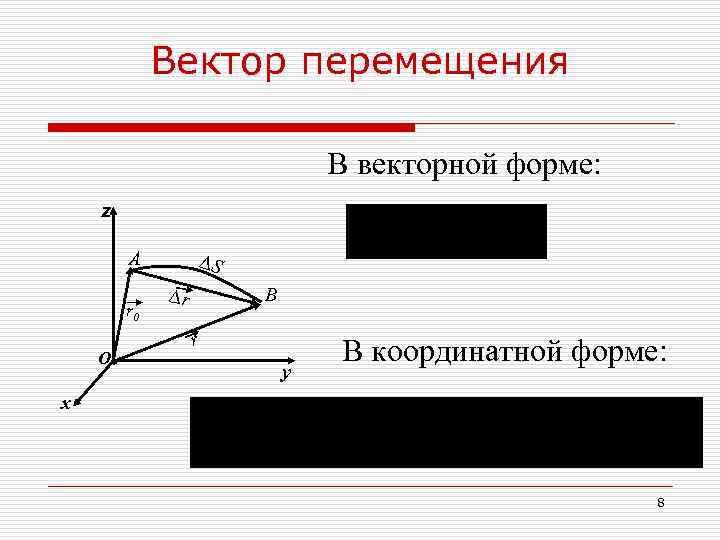
Траектория, путь, вектор перемещения Линия, которую описывает материальная точка, перемещаясь в пространстве, называется траекторией. Алгебраическая сумма длин траекторий, описанных точкой к данному моменту времени, называется длиной пути (∆S). Вектор, проведённый из ΔЅ ∆r начальной точки в конечную r 0 точку пути называется r О вектором перемещения (∆r). 6

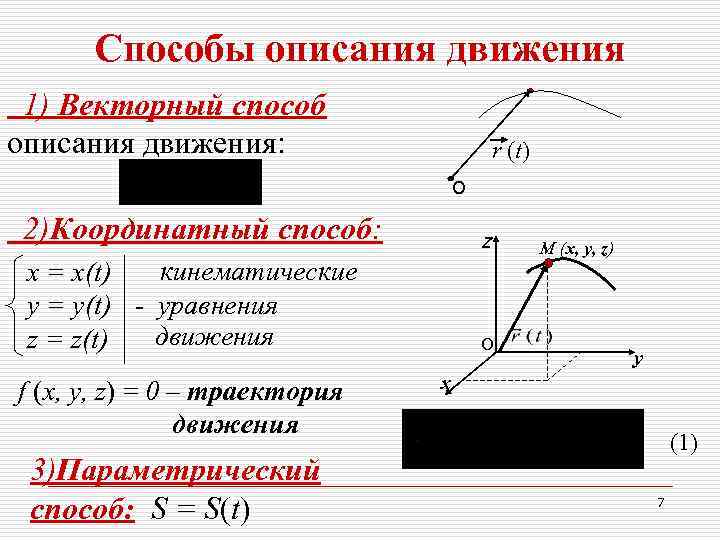
Способы описания движения 1) Векторный способ описания движения: r (t) О 2)Координатный способ: z M (x, y, z) x = x(t) кинематические y = y(t) - уравнения z = z(t) движения О у х f (x, y, z) = 0 – траектория движения (1) 3)Параметрический способ: S = S(t) 7

Вектор перемещения В векторной форме: z А ΔЅ ∆r В r 0 r О В координатной форме: у х 8

Скорость - векторная величина, определяющая быстроту и направление движения. Средняя скорость перемещения: ΔЅ М N <υ> Δr Средняя путевая скорость : υ1 ΔЅ τ Мгновенная скорость: М N Δr τ (2) υ2 9

Задание скорости в координатной форме Из формул (1) и (2) следует: 10

Вычисление пути υ По формуле (2): 1 d. S = υ(t)dt 2 Графически: элементарный путь d. S – площадь заштрихованной трапеции. t 1 dt t 2 t Графически: путь S – площадь криволинейной трапеции t 1 1 2 t 2. 11

Ускорение - это физическая величина, характеризующая быстроту изменения вектора скорости по величине и направлению. Среднее ускорение: υ1 ΔЅ Мгновенное ускорение: N М Δυ υ2 12

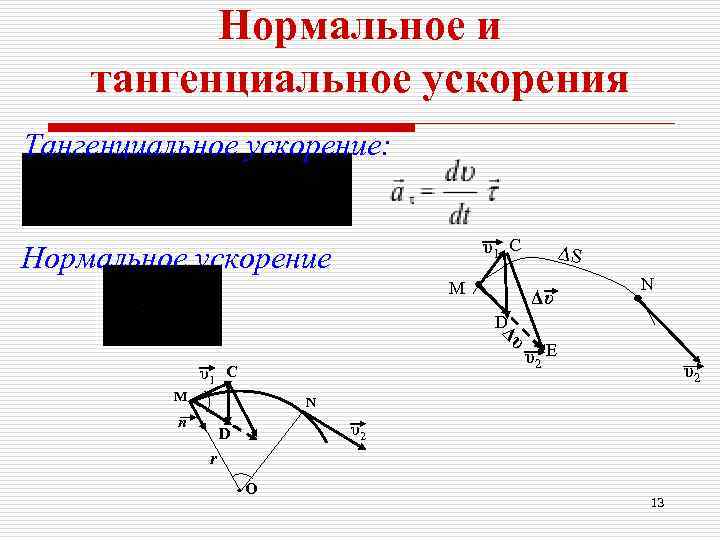
Нормальное и тангенциальное ускорения Тангенциальное ускорение: υ1 С Нормальное ускорение ΔЅ М N Δυ D Δυ υ2 Е υ1 С υ2 М N п D υ2 r О 13

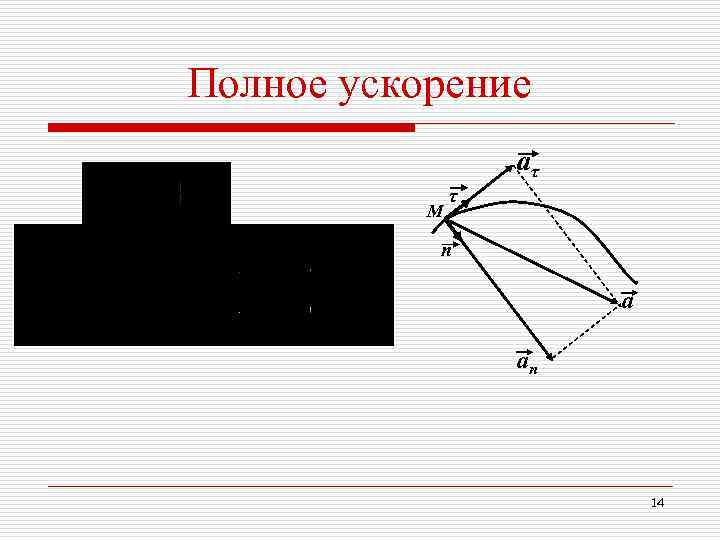
Полное ускорение аτ τ М п ап 14

Поступательное и вращательное движения Поступательное движение – это движение, при котором любая прямая, жестко связанная с движущимся телом, остается параллельной своему первоначальному положению. Вращательное движение – это движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения. Средняя угловая скорость Мгновенная угловая скорость 15

Угловая скорость Направление вектора угловой скорости находится по правилу буравчика (правилу правого винта). Единица угловой скорости: рад/с, Линейная скорость В векторной форме r Δφ Период вращения ΔЅ Частота вращения 16

Угловое ускорение Среднее угловое ускорение Мгновенное угловое ускорение Единица углового ускорения рад/с. 2 При ускоренном движении вектор сонаправлен век- тору , при замедленном – противоположен ему. 17 Ускоренное вращение Замедленное вращение

Связь между линейными и угловыми величинами S= R ; a = R ; an = 2 R. В случае равнопеременного движения точки по окружности ( = const): ω2 – ω02 = 2εφ 18