 “ Предмет математики настолько серьезен, что полезно не упускать случая, сделать его немного занимательным” Блез Паскаль французский математик
“ Предмет математики настолько серьезен, что полезно не упускать случая, сделать его немного занимательным” Блез Паскаль французский математик
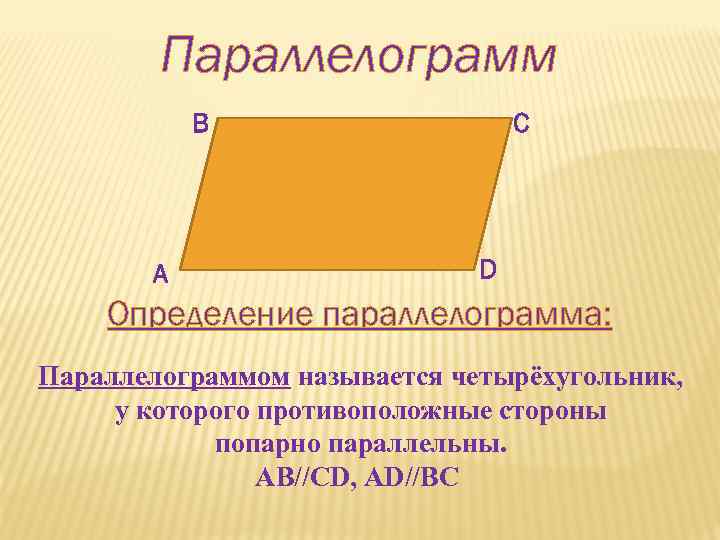 Параллелограмм В А С D Определение параллелограмма: Параллелограммом называется четырёхугольник, у которого противоположные стороны попарно параллельны. АВ//СD, AD//ВС
Параллелограмм В А С D Определение параллелограмма: Параллелограммом называется четырёхугольник, у которого противоположные стороны попарно параллельны. АВ//СD, AD//ВС
 В С О А D Свойства параллелограмма: 1) В параллелограмме противоположные стороны равны и противоположные углы равны. АВ=СD, ВС=АD;
В С О А D Свойства параллелограмма: 1) В параллелограмме противоположные стороны равны и противоположные углы равны. АВ=СD, ВС=АD;
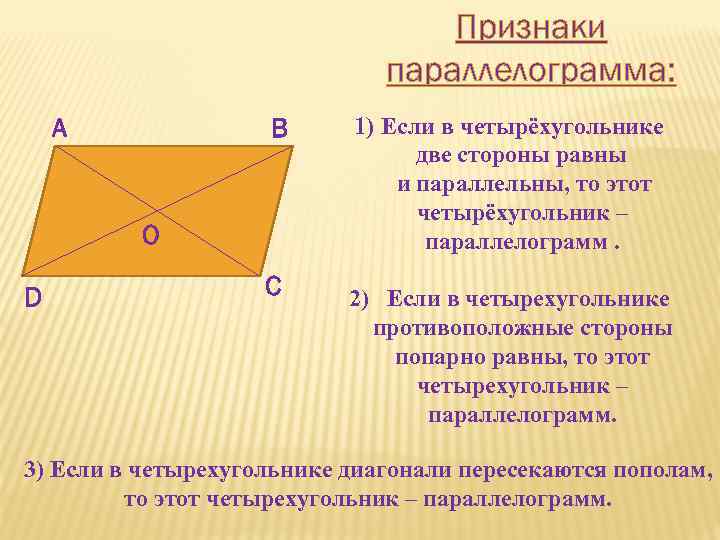 Признаки параллелограмма: А В О D С 1) Если в четырёхугольнике две стороны равны и параллельны, то этот четырёхугольник – параллелограмм. 2) Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм. 3) Если в четырехугольнике диагонали пересекаются пополам, то этот четырехугольник – параллелограмм.
Признаки параллелограмма: А В О D С 1) Если в четырёхугольнике две стороны равны и параллельны, то этот четырёхугольник – параллелограмм. 2) Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм. 3) Если в четырехугольнике диагонали пересекаются пополам, то этот четырехугольник – параллелограмм.
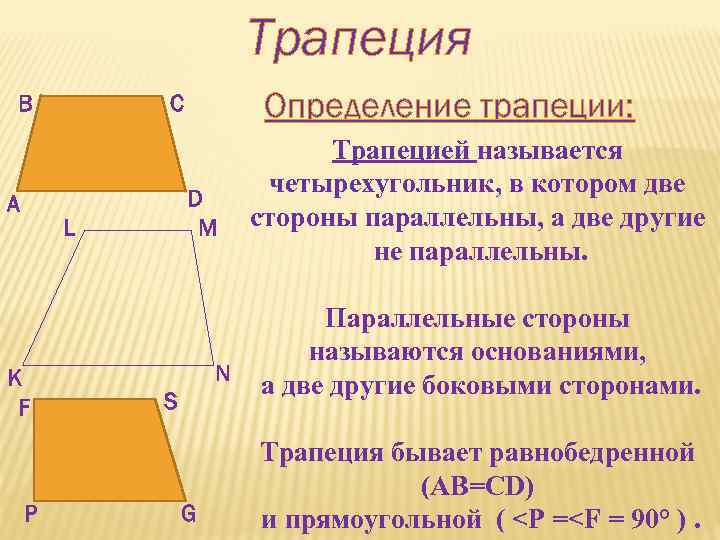 Трапеция В А D M L K F P Определение трапеции: С N S G Трапецией называется четырехугольник, в котором две стороны параллельны, а две другие не параллельны. Параллельные стороны называются основаниями, а две другие боковыми сторонами. Трапеция бывает равнобедренной (АВ=СD) и прямоугольной (
Трапеция В А D M L K F P Определение трапеции: С N S G Трапецией называется четырехугольник, в котором две стороны параллельны, а две другие не параллельны. Параллельные стороны называются основаниями, а две другие боковыми сторонами. Трапеция бывает равнобедренной (АВ=СD) и прямоугольной (
 Свойства равнобедренной трапеции: В А 1. В равнобедренной трапеции углы при основаниях равны.
Свойства равнобедренной трапеции: В А 1. В равнобедренной трапеции углы при основаниях равны.
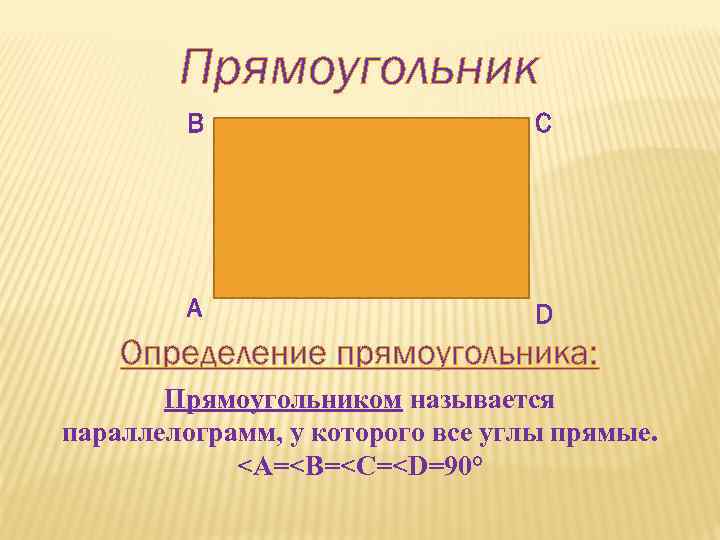 Прямоугольник В С А D Определение прямоугольника: Прямоугольником называется параллелограмм, у которого все углы прямые. <А=
Прямоугольник В С А D Определение прямоугольника: Прямоугольником называется параллелограмм, у которого все углы прямые. <А=
 Свойства прямоугольника: В С О А D 1. Все углы прямые.
Свойства прямоугольника: В С О А D 1. Все углы прямые.
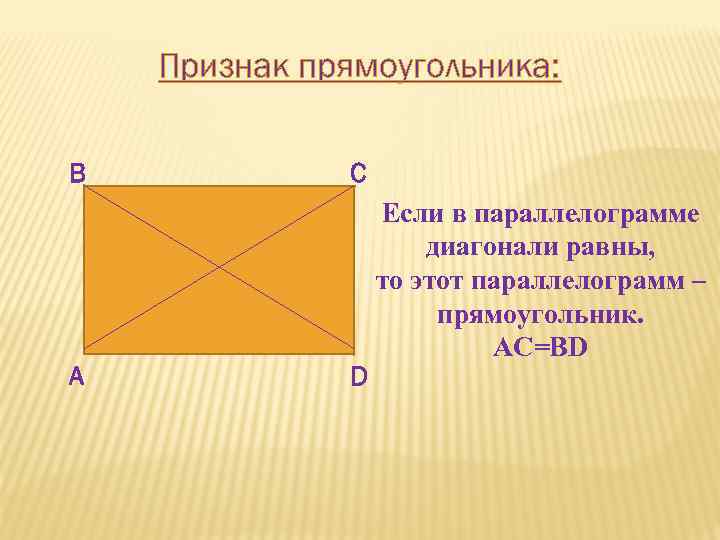 Признак прямоугольника: В А С D Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник. AC=BD
Признак прямоугольника: В А С D Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник. AC=BD
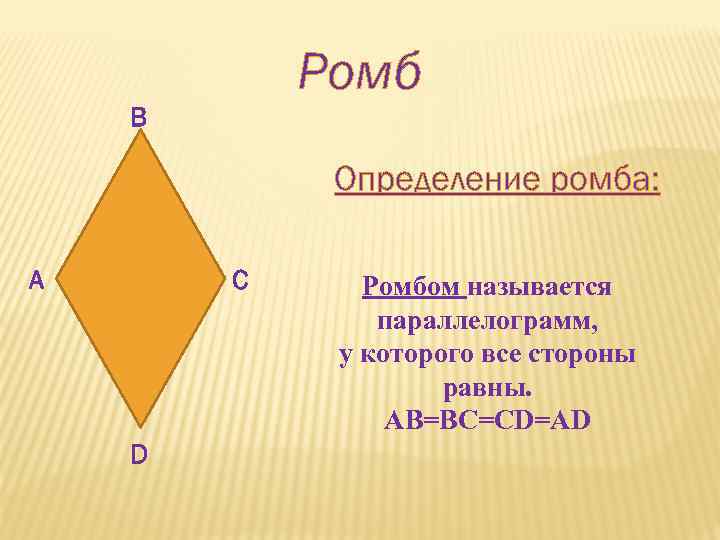 Ромб В Определение ромба: А С D Ромбом называется параллелограмм, у которого все стороны равны. АВ=ВС=СD=AD
Ромб В Определение ромба: А С D Ромбом называется параллелограмм, у которого все стороны равны. АВ=ВС=СD=AD
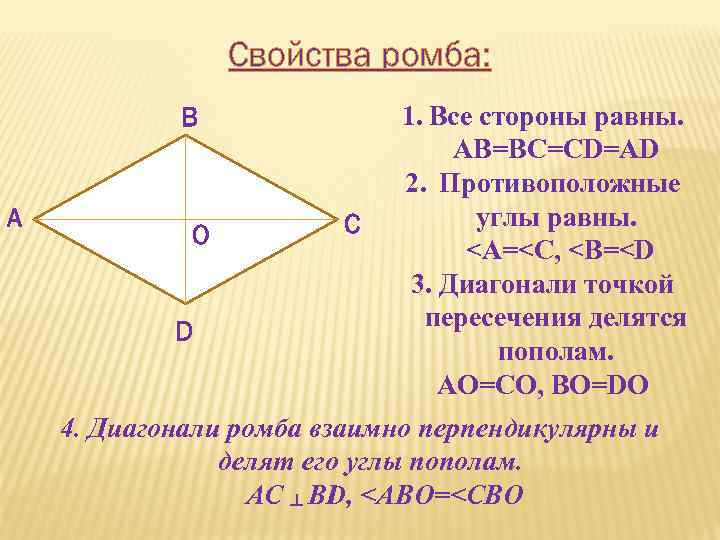 Свойства ромба: В А О D С 1. Все стороны равны. АВ=ВС=СD=AD 2. Противоположные углы равны.
Свойства ромба: В А О D С 1. Все стороны равны. АВ=ВС=СD=AD 2. Противоположные углы равны.
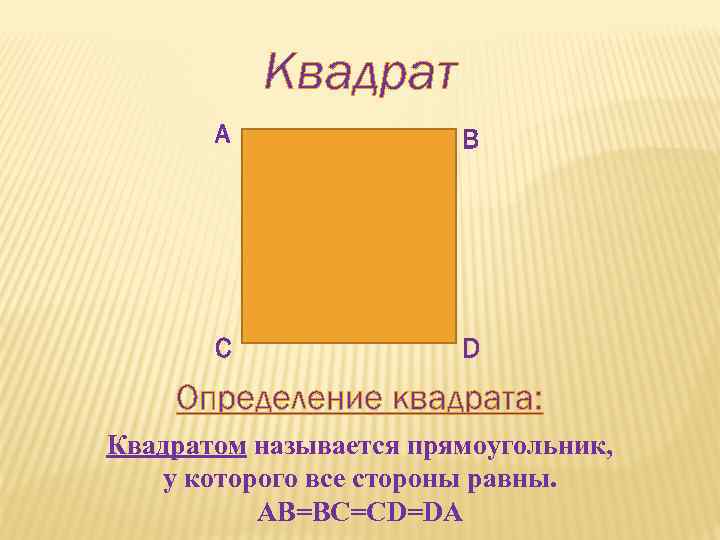 Квадрат А В С D Определение квадрата: Квадратом называется прямоугольник, у которого все стороны равны. AB=BC=CD=DA
Квадрат А В С D Определение квадрата: Квадратом называется прямоугольник, у которого все стороны равны. AB=BC=CD=DA
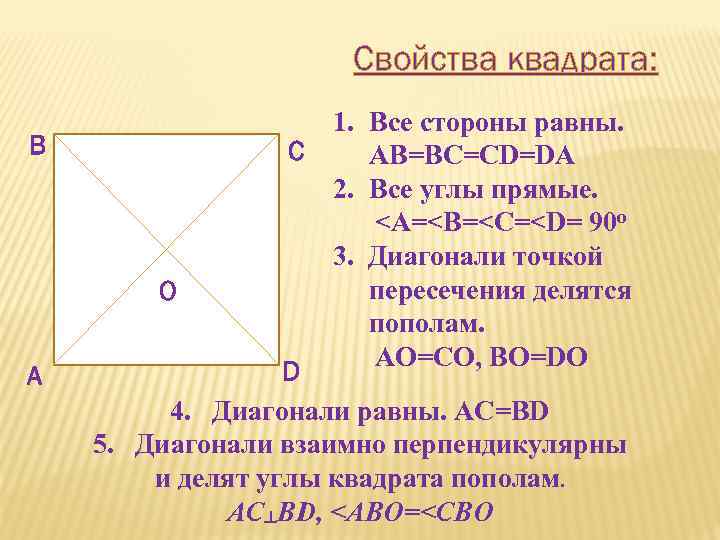 Свойства квадрата: В С О А 1. Все стороны равны. AB=BC=CD=DA 2. Все углы прямые.
Свойства квадрата: В С О А 1. Все стороны равны. AB=BC=CD=DA 2. Все углы прямые.