ПРЕДМЕТ И ЗАДАЧИ МЕТРОЛОГИИ Метрология в ее

ПРЕДМЕТ И ЗАДАЧИ МЕТРОЛОГИИ

Метрология в ее современном понимании - наука об измерениях, методах, средствах обеспечения их единства и способах достижения требуемой точности. В зависимости от цели различают три раздела метрологии: ü теоретическая üЗаконодательная üПрактическа. Я

Все объекты окружающего мира характеризуются своими свойствами Для количественного описания различных свойств процессов и физических тел вводится понятие величины. В ЕЛ И Ч И Н Ы реальные идеальные физические нефизические математические измеряемые оцениваемые

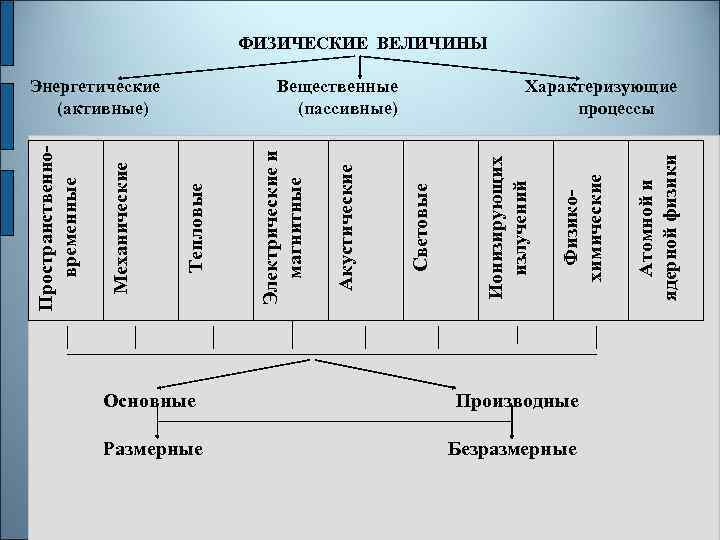ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ Основные Производные Размерные Безразмерные Атомной и ядерной физики Физикохимические Ионизирующих излучений Световые Акустические Электрические и магнитные Тепловые Механические Пространственновременные Энергетические Вещественные Характеризующие (активные) (пассивные) процессы

Системы единиц физических величин Под физической величиной понимается свойство, общее в качественном отношении для многих физических объектов (физических систем, их состояний и происходящих в них процессов), но в количественном отношении индивидуальное для каждого объекта. Для того чтобы можно было установить различия в количественном содержании свойств в каждом объекте, отображаемых физической величиной, вводится понятие размера физической величины. Совокупность ФВ, образованная в соответствии с принятыми принципами, когда одни величины принимаются за независимые, а другие являются их функциями, называется системой физических величин В Российской Федерации используется Международная система единиц СИ, введенная ГОСТ 8. 417 -2002 «ГСИ. Единицы физических величин»

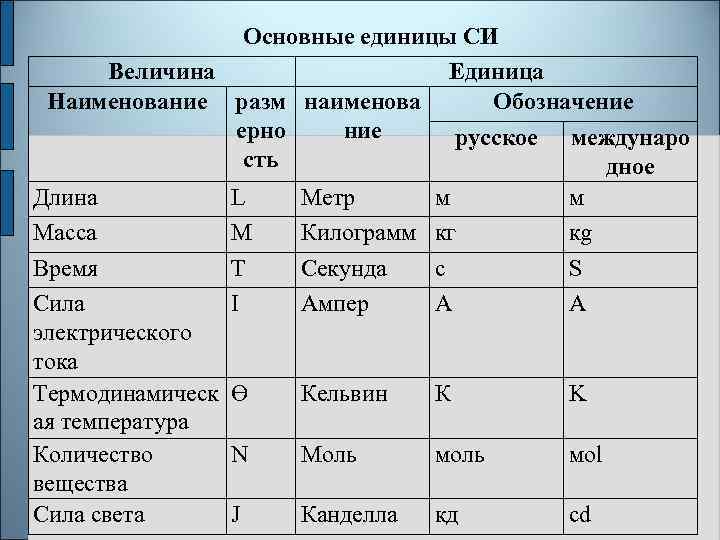Основные единицы СИ Величина Единица Наименование разм наименова Обозначение ерно ние русское междунаро сть дное Длина L Метр м м Масса M Килограмм кг кg Время T Секунда с S Сила I Ампер А A электрического тока Термодинамическ Ɵ Кельвин К K ая температура Количество N Моль мol вещества Сила света J Канделла кд cd

Определения основных единиц, соответствующие решениям Генеральной конференции по мерам и весам, следующие. Метр равен длине пути, проходимого светом в вакууме за 1/299792458 долю секунды. Килограмм равен массе международного прототипа килограмма. Секунда равна 9192631770 периодам излучения, соответствующего переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133. Ампер равен силе неизменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малой площади кругового сечения, расположенным на расстоянии 1 м один от другого в вакууме, вызывает на каждом участке проводника длиной 1 м силу взаимодействия, равную 2 *10 -7 Н Кельвин равен 1/273. 16 части термодинамической температуры тройной точки воды. Моль равен количеству вещества системы, содержащей столько же структурных элементов, сколько содержится атомов в углероде- 12 массой 0. 012 кг. Кандела равна силе света в заданном направлении источника, испускающего монохроматическое излучение частотой 540 • 1012 Гц энергетическая сила света которого в этом направлении составляет 1/683 Вт/ср.

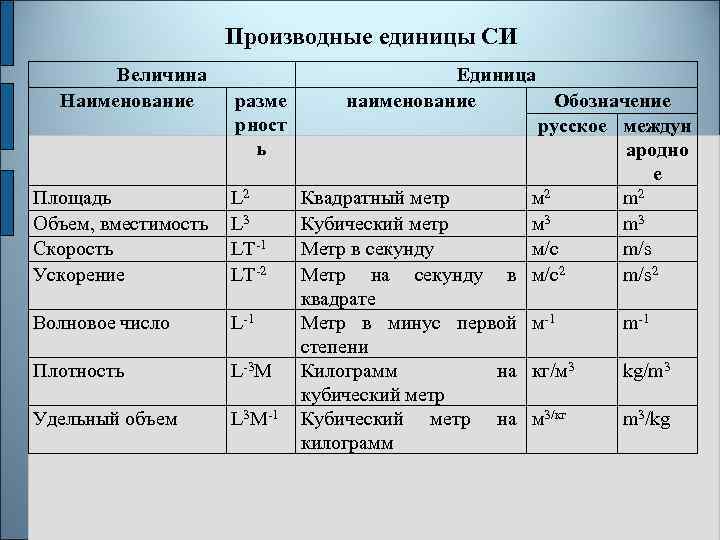Производные единицы СИ Величина Наименование Площадь Объем, вместимость Скорость Ускорение Волновое число Плотность Удельный объем Единица разме наименование Обозначение рност русское междун ь ародно е L 2 Квадратный метр м 2 m 2 L 3 Кубический метр м 3 m 3 LT-1 Метр в секунду м/с m/s LT-2 Метр на секунду в м/с2 m/s 2 квадрате L-1 Метр в минус первой м-1 m-1 степени L-3 M Килограмм на кг/м 3 kg/m 3 кубический метр L 3 M-1 Кубический метр на м 3/кг m 3/kg килограмм

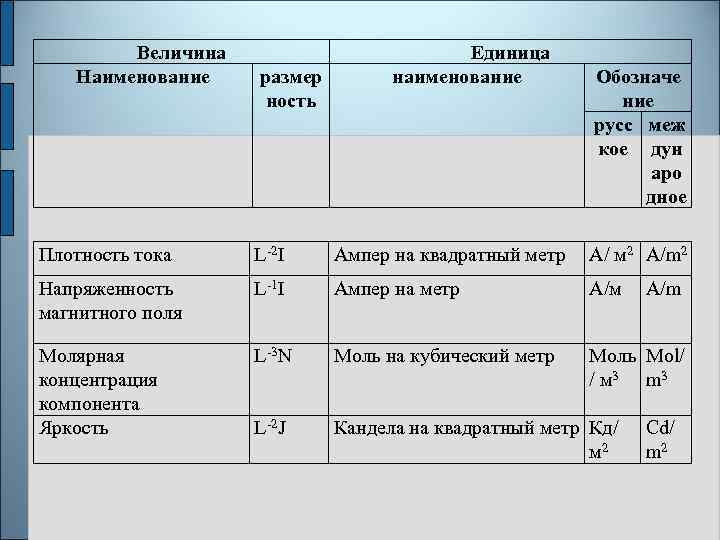Величина Наименование размер ность Единица наименование Обозначе ние русс меж кое дун аро дное Плотность тока L-2 I Ампер на квадратный метр А/ м 2 A/m 2 Напряженность магнитного поля L-1 I Ампер на метр А/м Молярная концентрация компонента Яркость L-3 N Моль на кубический метр Моль Mol/ / м 3 m 3 L-2 J Кандела на квадратный метр Кд/ м 2 A/m Cd/ m 2

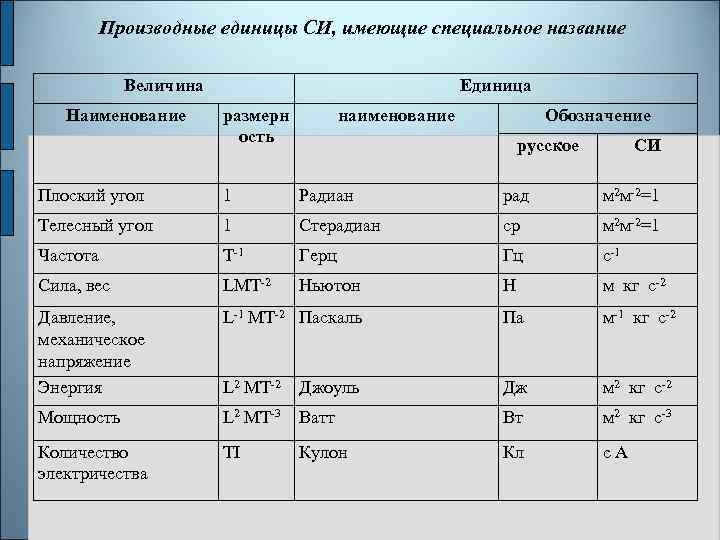Производные единицы СИ, имеющие специальное название Величина Наименование Единица размерн ость наименование Обозначение русское СИ Плоский угол 1 Радиан рад м 2 м-2=1 Телесный угол 1 Стерадиан ср м 2 м-2=1 Частота T-1 Герц Гц с-1 Сила, вес LМT-2 Ньютон Н м кг c-2 Давление, механическое напряжение Энергия L-1 МT-2 Паскаль Па м-1 кг c-2 L 2 МT-2 Джоуль Дж м 2 кг c-2 Мощность L 2 МT-3 Ватт Вт м 2 кг c-3 Количество электричества ТI Кл с А Кулон

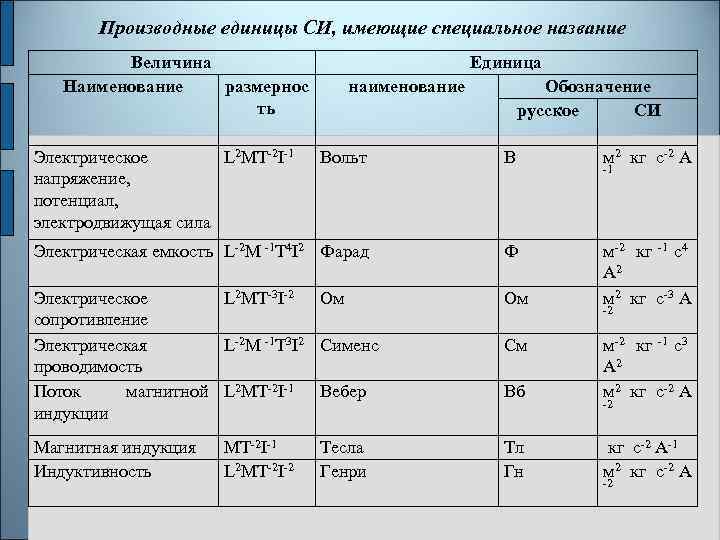Производные единицы СИ, имеющие специальное название Величина Наименование размернос ть Электрическое L 2 МT-2 I-1 напряжение, потенциал, электродвижущая сила Единица наименование Обозначение русское СИ Вольт В м 2 кг c-2 А Электрическая емкость L-2 М -1 T 4 I 2 Фарад Ф Электрическое L 2 МT-3 I-2 Ом сопротивление Электрическая L-2 М -1 T 3 I 2 Сименс проводимость Поток магнитной L 2 МT-2 I-1 Вебер индукции Ом м-2 кг -1 c 4 А 2 м 2 кг c-3 А Вб м-2 кг -1 c 3 А 2 м 2 кг c-2 А Магнитная индукция Индуктивность Тл Гн кг c-2 А-1 м 2 кг c-2 А МT-2 I-1 L 2 МT-2 I-2 Тесла Генри См -1 -2 -2 -2

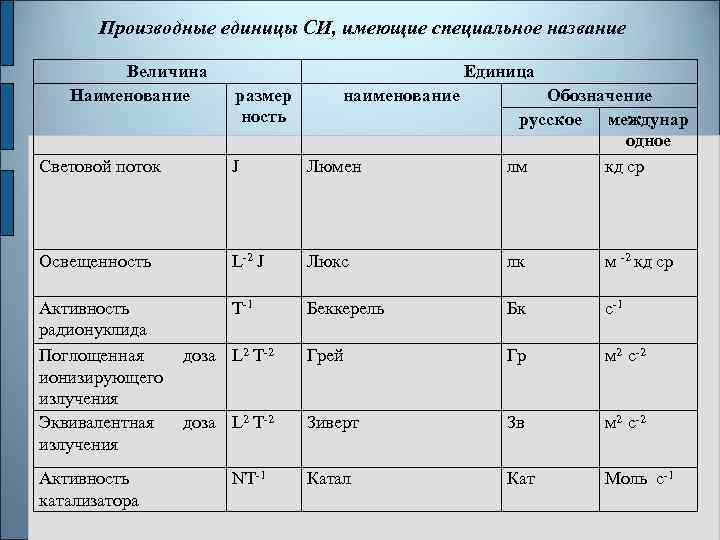Производные единицы СИ, имеющие специальное название Величина Наименование Единица размер ность Световой поток J Люмен Обозначение русское междунар одное лм кд ср Освещенность L-2 J Люкс лк м -2 кд ср Активность Т-1 радионуклида Поглощенная доза L 2 T-2 ионизирующего излучения Эквивалентная доза L 2 T-2 излучения Беккерель Бк с-1 Грей Гр м 2 с-2 Зиверт Зв м 2 с-2 Активность катализатора Катал Кат Моль с-1 NT-1 наименование

Единицы ФВ делятся на системные и внесистемные. Внесистемные единицы по отношению к единицам СИ разделяются на четыре вида: - допускаемые наравне с единицами СИ (ед. массы- тонна, времени – минута и т. д. ); -допускаемые к применению в специальных областях (астрономическая единица, парсек, световой год, электронвольт в физике); -временно допускаемые к применению наравне с единицами СИ (морская миля – в морском деле, карат – в ювелирном деле); -изъятые из обращения ( мощность – лошадиная сила, давление –мм ртутного столба).

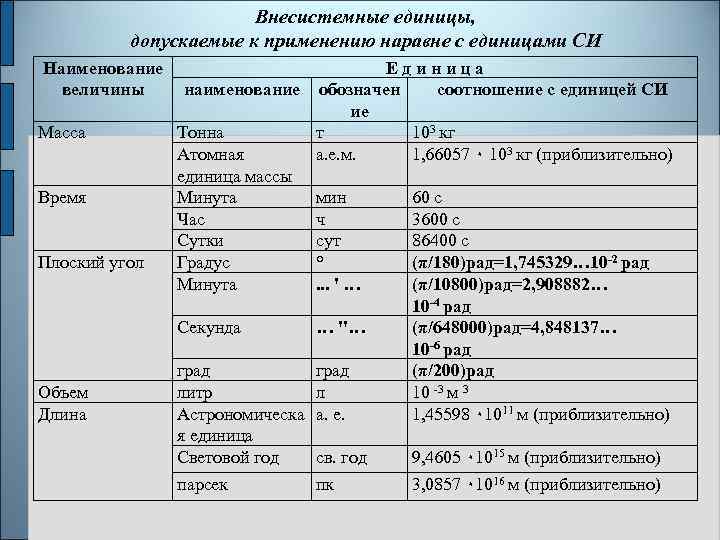Внесистемные единицы, допускаемые к применению наравне с единицами СИ Наименование наименование величины Масса Время Тонна Атомная единица массы Минута Час Сутки Градус Минута Е д и н и ц а обозначен соотношение с единицей СИ ие т 103 кг а. е. м. 1, 66057 ٠ 103 кг (приблизительно) Секунда Плоский угол Объем Длина мин ч сут °. . . ' … … "… град литр Астрономическа я единица Световой год град л а. е. 60 с 3600 с 86400 с (π/180)рад=1, 745329… 10 -2 рад (π/10800)рад=2, 908882… 10 -4 рад (π/648000)рад=4, 848137… 10 -6 рад (π/200)рад 10 -3 м 3 1, 45598 ٠ 1011 м (приблизительно) св. год 9, 4605 ٠ 1015 м (приблизительно) парсек пк 3, 0857 ٠ 1016 м (приблизительно)

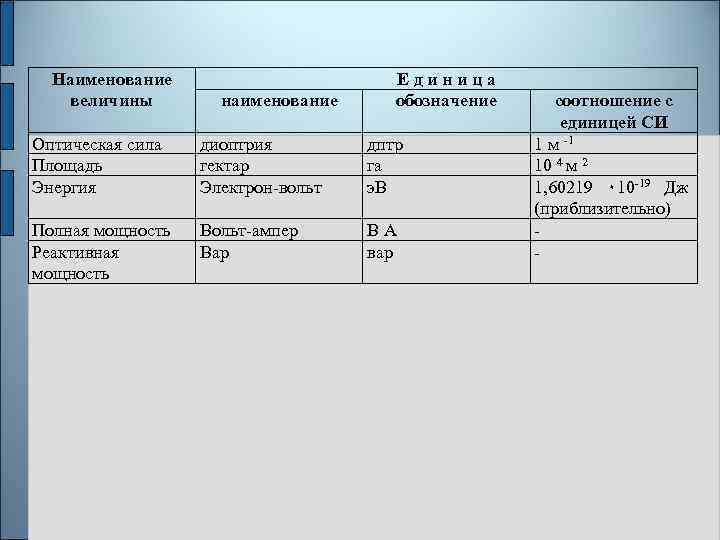Наименование величины наименование Е д и н и ц а обозначение Оптическая сила Площадь Энергия диоптрия гектар Электрон-вольт дптр га э. В Полная мощность Реактивная мощность Вольт-ампер Вар В А вар соотношение с единицей СИ 1 м -1 10 4 м 2 1, 60219 ٠ 10 -19 Дж (приблизительно) -

В науке и технике широко распространены относительные и логарифмические единицы измерения. Относительная величина представляет собой безразмерное отношение физической величины к одноименной физической величине, принимаемой за исходную. Логарифмическая величина представляет собой логарифм (десятичный, натуральный или при основании 2) безразмерного отношения двух одноименных физических величин.

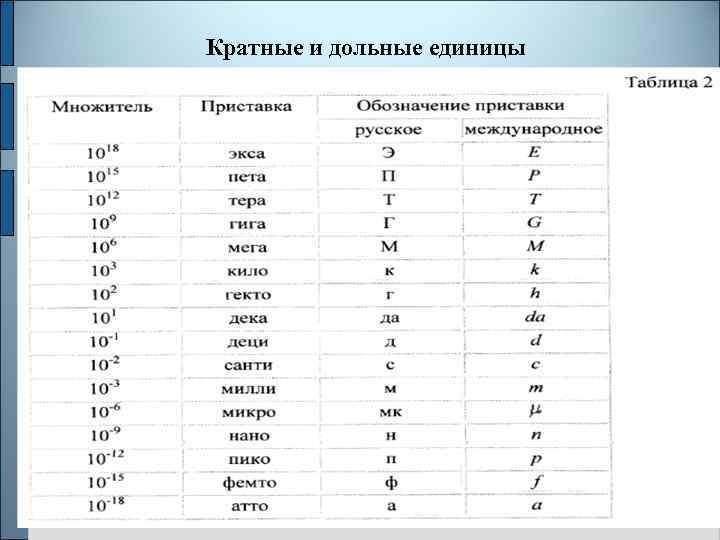Кратные и дольные единицы

Воспроизведение единиц физических величин Единство должно обеспечиваться при любой точности, необходимой науке и технике. На государственном уровне деятельность по обеспечению единства измерений регламентируется стандартами Государственной системы обеспечения единства измерений (ГСИ), нормативными документами органов метрологической службы и Законом об обеспечении единства измерений (Федеральный закон Российской Федерации от 26 июня 2008 г. N 102 -ФЗ "Об обеспечении единства измерений") -ВОСПРОИЗВЕДЕНИЕ ОСНОВНОЙ ЕДИНИЦЫ – это воспроизведение единицы путем создания фиксированной по размеру в соответствии с определением единицы -ВОСПРОИЗВЕДЕНИЕ ПРОИЗВОДНОЙ ЕДИНИЦЫ – это определение значения ФВ в указанных единицах на основании косвенных измерений других величин, функционально связанных с измеряемой

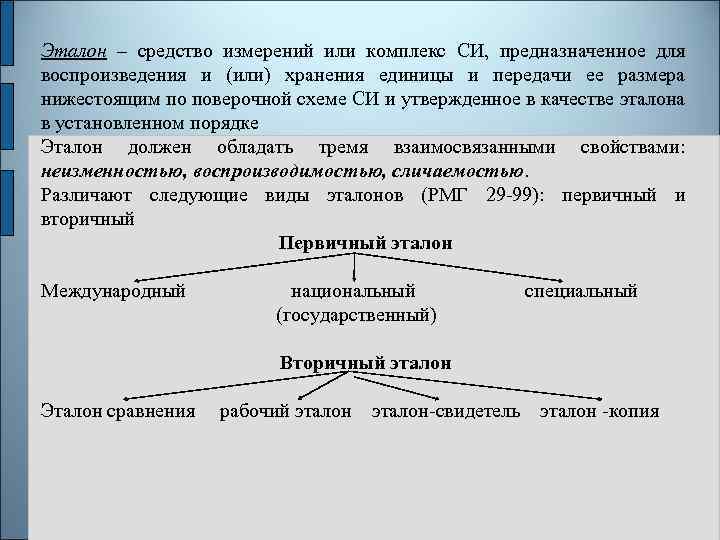Эталон – средство измерений или комплекс СИ, предназначенное для воспроизведения и (или) хранения единицы и передачи ее размера нижестоящим по поверочной схеме СИ и утвержденное в качестве эталона в установленном порядке Эталон должен обладать тремя взаимосвязанными свойствами: неизменностью, воспроизводимостью, сличаемостью. Различают следующие виды эталонов (РМГ 29 -99): первичный и вторичный Первичный эталон Международный национальный специальный (государственный) Вторичный эталон Эталон сравнения рабочий эталон-свидетель эталон -копия

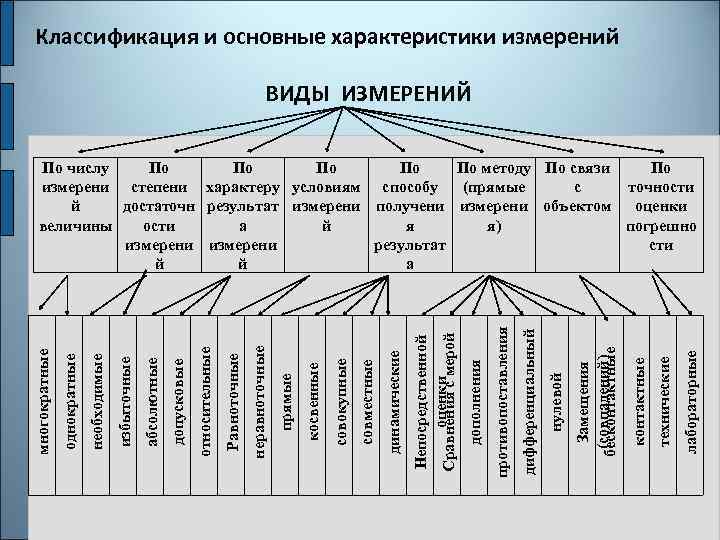лабораторные технические контактные Замещения (совпадений) бесконтактные нулевой дифференциальный противопоставления дополнения Непосредственной оценки Сравнения с мерой динамические совместные совокупные косвенные прямые неравноточные Равноточные относительные допусковые абсолютные избыточные необходимые однократные многократные Классификация и основные характеристики измерений ВИДЫ ИЗМЕРЕНИЙ По числу По По По методу По связи По измерени степени характеру условиям способу (прямые с точности й достаточн результат измерени получени измерени объектом оценки величины ости а й я я) погрешно измерени результат сти й й а

Прямые измерения – основа наиболее сложных измерений, в соответствии с РМГ 29 -99 различают следующие методы: • Метод непосредственной оценки, при котором значение величины определяют непосредственно по отсчетному устройству измерительного прибора • Метод сравнения с мерой, где измеряемую величину сравнивают с величиной, воспроизводимой с мерой • Метод дополнения, если значение измеряемой величины дополняется мерой этой же величины с таким расчетом, чтобы на прибор сравнения воздействовала сумма, равная заранее заданному значению • Дифференциальный метод характеризуется измерением разности между измеряемой величиной и известной величиной, воспроизводимой мерой. • Нулевой метод аналогичен дифференциальному, но разность между измеряемой величиной и мерой сводится к нулю • Метод замещения –метод сравнения с мерой, в котором измеряемую величину замещают известной величиной, воспроизводимой мерой

По условиям, определяющим точность результата, измерения делятся на три класса: 1. Измерения максимально возможной точности 2. Контрольно-поверочные измерения 3. Технические измерения По способу выражения результатов измерений различают абсолютные и относительные измерения. Основными характеристиками измерений являются: принцип измерений, метод измерений, погрешность, точность, правильность и достоверность.

ПОГРЕШНОСТИ ИЗМЕРЕНИЙ. Любая ошибка, которая может вкрасться в расчет, вкрадется в него.

Истинные значения физических величин – это значения, идеальным образом отражающие свойства данного объекта как в количественном, так и в качественном отношении. Они не зависят от средств нашего познания и являются абсолютной истиной. Под действительным значением физической величины понимают ее значение, найденной экспериментально и настолько приближенное к истинному, что для данной цели оно может быть использовано вместо него. За действительное значение физической величины принимают значение, измеренное с помощью эталонных (образцовых) Для характеристики точности приборов и измерений приборов.

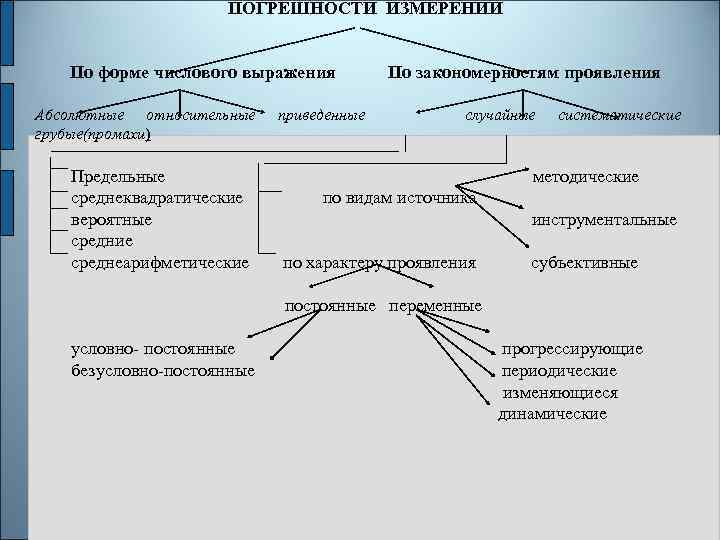ПОГРЕШНОСТИ ИЗМЕРЕНИЙ По форме числового выражения Абсолютные относительные грубые(промахи) Предельные среднеквадратические вероятные средние среднеарифметические приведенные По закономерностям проявления случайные систематические методические по видам источника инструментальные по характеру проявления субъективные постоянные переменные условно- постоянные безусловно-постоянные прогрессирующие периодические изменяющиеся динамические

Для характеристики точности приборов и измерений вводят понятие погрешности. Погрешности классифицируют: - по способу выражения погрешности способов и методов измерения (абсолютная, относительная, приведенная) Абсолютная погрешность – это разность между измеренным и действительным значением величины. Абсолютная погрешность, которая берется с противоположным знаком, называется поправкой. Δ = Х -Хи Относительной погрешностью называют отношение абсолютной погрешности к действительному значению величины, она может выражаться в долях единиц или процентах. Относительная точность характеризует точность измерений. Δ = ± Δ / Хи или в процентах: δ = ± Δ / Хи· 100 точность измерений.

Приведенная погрешность – это отношение абсолютной погрешности к номинальному (максимальное значение шкалы прибора) значению величины. Приведенная погрешность определяет класс точности измерительного прибора, может выражаться в долях единиц или процентах. γ = ± Δ / ХN· 100 Чувствительностью прибора называют отношение перемещения стрелки к измеряемой величине, обратная величина называется постоянной прибора или ценой деления. Цену деления можно определить как отношение номинального значения прибора к числу делений шкалы.

-по характеру проявления (систематические, случайные, погрешности оператора) Систематическая погрешность обусловлена факторами, которые можно учесть. Она остается постоянной или изменяется по закону, т. о. систематическую погрешность можно учесть с помощью соответствующих поправок. Случайная погрешность возникает в результате отдельных случайных факторов, которые не подлежат непосредственному учету, т. к. она изменяется по случайному закону, ее не возможно определить экспериментально. Оценку случайной погрешности можно произвести методом теории вероятности при большом количестве повторяемых измерений. Погрешность оператора возникает из-за ошибочной записи, неправильного определения цены деления и т. д. Чаще всего эту погрешность просто

-по условиям эксплуатации (основная, дополнительная) Основная погрешность – это погрешность способов измерения в нормальных условиях эксплуатации (согласно с данными приведенными в паспорте прибора) Дополнительная погрешность – это погрешность способов измерения, которая возникает при отклонении от нормальных условий эксплуатации. В общем случае погрешность является случайной функцией времени, которая отличается от классических функций математического анализа тем, что нельзя сказать, какое значение она примет в момент времени t. Можно указать лишь вероятности появления ее значений в том или ином интервале. В серии экспериментов, состоящих из ряда многократных наблюдений, мы получаем одну реализацию этой функции. При повторении серии при тех же значениях величин, характеризующих факторы второй группы, неизбежно получаем новую реализацию, отличающуюся от первой.

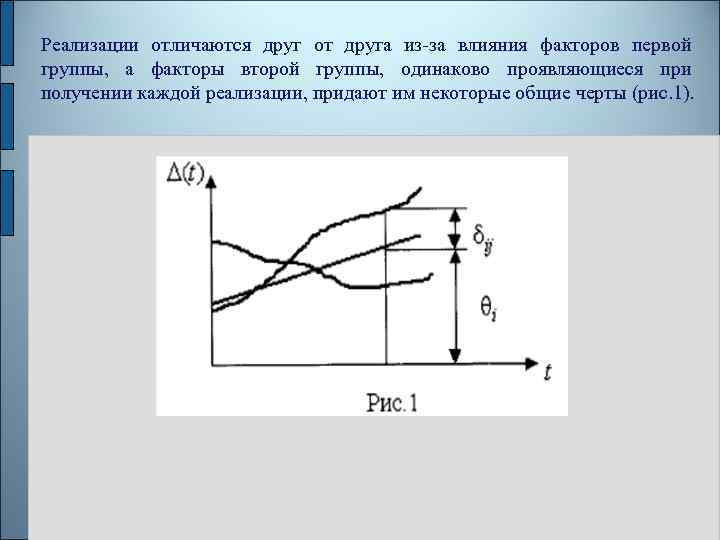Реализации отличаются друг от друга из-за влияния факторов первой группы, а факторы второй группы, одинаково проявляющиеся при получении каждой реализации, придают им некоторые общие черты (рис. 1).

Описание случайных погрешностей с помощью функций распределения. Рассмотрим результат наблюдений X за постоянной физической величиной как случайную величину, принимающую различные значения , в различных наблюдения за ней. Значения будем называть результатами отдельных наблюдений. Наиболее универсальный способ описания случайных величин заключается в отыскании их интегральных или дифференциальных функций распределения. Под интегральной функцией распределения результатов наблюдений понимается у зависимость вероятности того, что результат наблюдения опыте окажется меньшим некоторого текущего значения х, от самой величины х: Здесь и в дальнейшем большие буквы используются для обозначения случайных величин, а маленькие - значений, принимаемых случайными величинами.

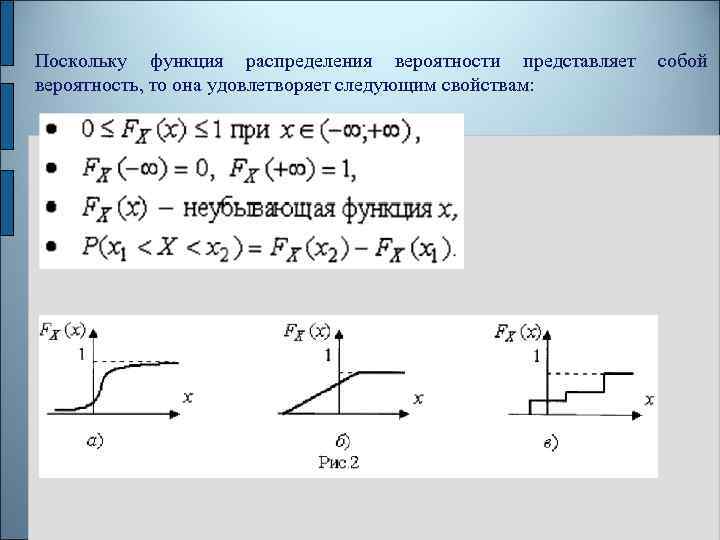Поскольку функция распределения вероятности представляет собой вероятность, то она удовлетворяет следующим свойствам:

Более наглядным является описание свойств результатов наблюдений и Случайных погрешностей с помощью дифференциальной функции распределения иначе называемой плотностью распределения вероятностей Физический смысл состоит в том, что произведение представляет вероятность попадания случайной величины X в интервал от х до х + dх , т. е.

Необходимо отметить, что результаты наблюдений в значительной степени сконцентрированы вокруг истинного значения измеряемой величины и по мере приближения к нему элементы вероятности их появления возрастают. Это дает основание принять за оценку истинного значения измеряемой величины координату центра тяжести фигуры, образованной осью абсцисс и кривой распределения, и называемую математическим ожиданием результатов наблюдений

В заключение можно дать более строгое определение постоянной систематической и случайной погрешностей. Систематической постоянной погрешностью называется отклонение математического ожидания результатов наблюдений от истинного значения измеряемой величины: а случайной погрешностью - разность между результатом единичного наблюдения и математическим ожиданием результатов. В этих обозначениях истинное значение измеряемой величины составляет

Моменты случайных погрешностей Функция распределения является самым универсальным способом описания поведения случайных погрешностей. Однако для определения функций распределения необходимо проведение весьма кропотливых научных исследований и обширных вычислительных работ. Поэтому к такому способу описания случайных погрешностей прибегают иногда при исследовании принципиально новых мер и измерительных приборов. Значительно чаще бывает достаточно охарактеризовать случайные погрешности с помощью ограниченного числа специальных величин, называемых моментами. Начальным моментом n-го порядка результатов наблюдений называется интеграл вида представляющий собой" математическое ожидание степени при n=1 т. е. первый начальный момент совпадает с математическим ожиданием результатов измерений.

Центральным моментом n-го порядка результатов наблюдений называется интеграл вида Вычислим первый центральный момент: Таким образом, первый центральный момент результатов наблюдений равен нулю. Важно отметить, что начальные и центральные моменты случайных погрешностей совпадают между собой и с центральными моментами результатов наблюдений, поскольку математическое ожидание случайных погрешностей равно нулю. Особое значение наряду с математическим ожиданием результатов наблюдений имеет второй центральный момент, называемый дисперсией результатов наблюдений. При n=2

Дисперсия погрешности равна дисперсии результатов наблюдений и является характеристикой их рассеивания относительно математического ожидания. Если математическое ожидание результатов наблюдений можно рассматривать в механической интерпретации как абсциссу центра тяжести фигуры, заключенной между кривой распределения и осью Ох, то дисперсия является аналогом момента инерции этой фигуры относительно вертикальной оси, проходящей через центр тяжести. Дисперсия имеет размерность квадрата измеряемой величины, поэтому она не Совсем удобна в качестве характеристики рассеивания. Значительно чаще в качестве последней используется положительное значение корня квадратного из дисперсии, называемое средним квадратическим отклонением результатов наблюдений: С помощью среднеквадратического отклонения можно оценить вероятность того, что при однократном наблюдении случайная погрешность по абсолютной величине не превзойдет некоторой наперед заданной величины

Для этого рассмотрим формулу, известную как неравенство Чебышева: Полагая можно найти вероятность того, что результат однократного наблюдения отличается от истинного значения на величину, большую утроенного среднеквадратического отклонения, т. е. вероятность того, что случайная погрешность окажется больше

Неравенство Чебышева дает только нижнюю границу для вероятности меньше которой она не может быть ни при каком распределении. Обычно значительно больше 0. 89. Так, например, в случае нормального распределения погрешностей эта вероятность составляет 0. 9973. Математическое ожидание и дисперсия являются наиболее часто применяемыми моментами, поскольку они определяют наиболее важные черты распределения: положение центра распределения и степень его разбросанности. Для более подробного описания распределения используются моменты более высоких порядков. Третий момент случайных погрешностей служит характеристикой асимметрии, или скошенности распределения. В общем случае любой нечетный момент случайной погрешности характеризует асимметрию распределения.

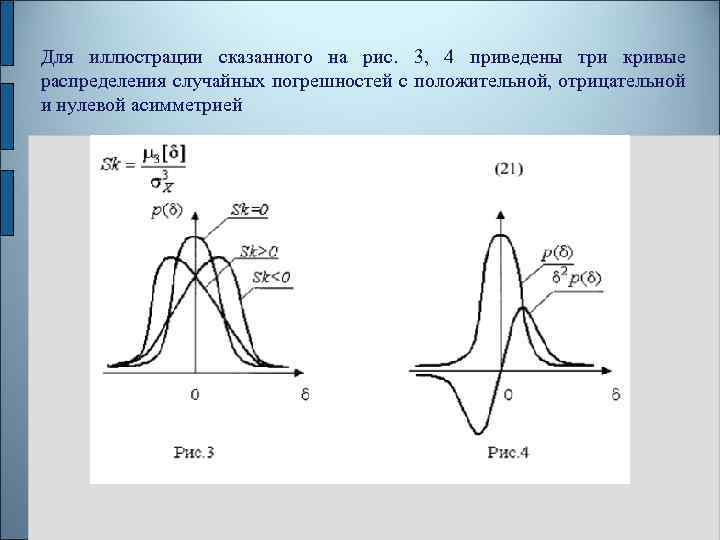Для иллюстрации сказанного на рис. 3, 4 приведены три кривые распределения случайных погрешностей с положительной, отрицательной и нулевой асимметрией

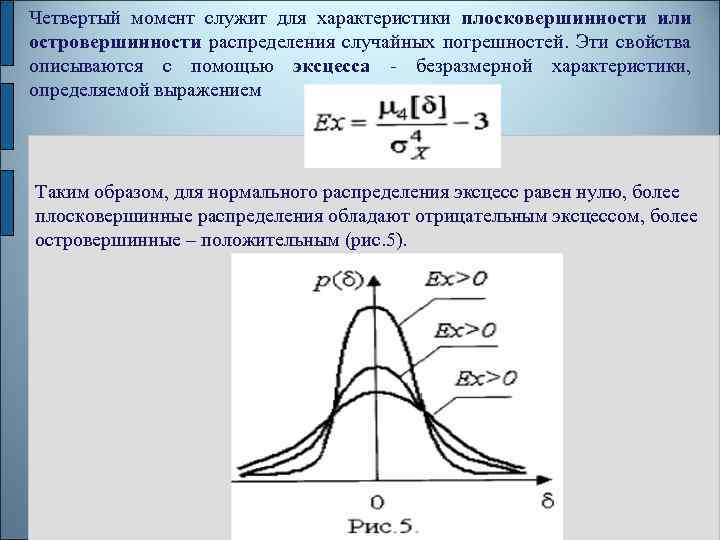Четвертый момент служит для характеристики плосковершинности или островершинности распределения случайных погрешностей. Эти свойства описываются с помощью эксцесса - безразмерной характеристики, определяемой выражением Таким образом, для нормального распределения эксцесс равен нулю, более плосковершинные распределения обладают отрицательным эксцессом, более островершинные – положительным (рис. 5).

Виды распределения результатов наблюдения и случайных погрешностей Случайная погрешность измерения образуется под влиянием большого числа факторов, сопутствующих процессу измерения. В каждой конкретной ситуации работает свой механизм образования погрешности. Поэтому естественно предположить, что каждой ситуации должен соответствовать свой тип распределения погрешности. Однако во многих случаях имеются возможности еще до проведения измерений сделать некоторые предположения о форме функции распределения, так что после проведения измерений остается только определить значения некоторых параметров, входящих в выражение для предполагаемой функции распределения. Случайная погрешность характеризует неопределенность наших знаний об истинном значении измеряемой величины, полученных в результате проведенных наблюдений. Согласно К. Шеннону мерой неопределенности ситуации, описываемой случайной величиной X, является энтропия

Можно предположить, что любой процесс измерения формируется таким образом, что неопределенность результата наблюдений оказывается наибольшей в некоторых пределах, определяемых допускаемыми значениями погрешности. Широкое распространение нормального распределения погрешностей в практике измерений объясняется центральной предельной теоремой теории вероятностей, являющейся одной из самых замечательных математических теорем, в разработке которой многие крупнейшие математики - Муавр, Лаплас, Гаусс, Чебышев и Ляпунов. Центральная предельная теорема утверждает, что распределение случайных погрешностей будет близко в нормальному всякий раз, когда результаты наблюдения формируются под влиянием большого числа независимо действующих факторов, каждый из которых оказывает лишь незначительное действие по сравнению с суммарным действием всех остальных.

Точечные оценки истинного значения и среднеквадратического отклонения К точечным оценкам предъявляется ряд требований, определяющих их пригодность для описания самих параметров. 1. Оценка называется состоятельной, если при увеличении числа наблюдений она приближается (сходится по вероятности) к значению оцениваемого параметра. 2. Оценка называется несмещенной, если ее математическое ожидание равно оцениваемому параметру. 3. Оценка называется эффективной, если ее дисперсия меньше дисперсии любой другой оценки данного параметра. Используют для расчетов метод Фишера максимального правдоподобия метод наименьших квадратов: некоторые постоянные, именно среднее арифметическое обращает в минимум дисперсию

Оценка с помощью интервалов Смысл оценки параметров с помощью интервалов заключается в нахождении интервалов, называемых доверительными, между границами которых с определенными вероятностями (доверительными) находятся истинные значения оцениваемых параметров. Полученный доверительный интервал, построенный с помощью среднего арифметического результатов n независимых повторных наблюдений, в раз короче интервала, вычисленного по результату одного наблюдения, хотя доверительная вероятность для них одинакова. Это говорит о том, что сходимость измерений растет пропорционально корню квадратному из числа наблюдений. В тех случаях, когда распределение случайных погрешностей не является нормальным, все же часто пользуются распределением Стьюдента с приближением, степень которого остается неизвестной. Кроме того, на основании центральной предельной теоремы теории вероятностей можно утверждать, что при достаточно большом числе наблюдений распределение среднего арифметического как суммы случайных величин будет сколь угодно близким к нормальному

Обнаружение грубых погрешностей Вопрос о том, содержит ли данный результат наблюдений грубую погрешность, решается общими методами проверки статистических гипотез. Для проверки гипотезы следует воспользоваться распределениями величин Функции их распределения определяют методами теории вероятностей Если вычисленное по опытным данным значение окажется меньше , то гипотеза принимается; в противном случае ее следует отвергнуть как противоречащую данным наблюдений. Тогда результат или соответственно приходится рассматривать как содержащий грубую погрешность и не принимать его во внимание при дальнейшей обработке результатов наблюдений

Классификация систематических погрешностей В зависимости от причин возникновения рассматриваются четыре вида систематических погрешностей: 1. Погрешности метода, или теоретические погрешности, проистекающие от ошибочности или недостаточной разработки принятой теории метода измерений в целом или от допущенных упрощений при проведении измерений 2. Инструментальные погрешности, зависящие от погрешностей применяемых средств измерений. Среди инструментальных погрешностей в отдельную группу выделяются погрешности схемы, не связанные с неточностью изготовления средств измерения и обязанные своим происхождением самой структурной схеме средств измерений. Исследование инструментальных погрешностей является предметом специальной дисциплины - теории точности измерительных устройств. 3. Погрешности, обусловленные неправильной установкой и взаимным расположением средств измерения, являющихся частью единого комплекса, несогласованностью их характеристик, влиянием внешних температурных, гравитационных, радиационных и других полей, нестабильностью источников питания, несогласованностью входных и выходных параметров электрических цепей приборов и так далее 4. Личные погрешности, обусловленные индивидуальными особенностями наблюдателя. Такого рода погрешности вызываются, например, запаздыванием или опережением при регистрации сигнала, неправильным отсчетом десятых долей деления шкалы, асимметрией, возникающей при установке штриха посередине между двумя рисками.

Введение поправок. Неисключенная систематическая погрешность Для исправления результата наблюдения его складывают только со средним арифметическим значением поправки: соответственно исправленный и неисправленный результаты наблюдений, q среднее арифметическое значение поправки, определяемые экспериментально. Систематическая погрешность, остающаяся после введения поправок на ее наиболее существенные составляющие включает в себя ряд элементарных составляющих, называемых неисключенными остатками систематической погрешности. К их числу относятся: • погрешности определения поправок; • погрешности, зависящие от точности измерения влияющих величин, входящих в формулы для определения поправок; • погрешности, связанные с колебаниями влияющих величин (температуры окружающей среды, напряжения питания и т. д. ).

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ И ИХ ЕДИНИЦЫ Мелочи не играют решающей роли. Они решают всё Под физической величиной понимается свойство, общее в качественном отношении для многих физических объектов (физических систем, их состояний и происходящих в них процессов), но в количественном отношении индивидуальное для каждого объекта. Система СГС. Система единиц физических величин СГС, в которой основными единицами являются сантиметр как единица длины, грамм как единица массы и секунда как единица времени, была установлена в 1881 г. Система МКГСС. Применение килограмма как единицы веса, а в последующем как единицы силы вообще, привело в конце XIX века к формированию системы единиц физических величин с тремя основными единицами: метр - единица длины, килограмм-сила - единица силы и секунда - единица времени. Система МКС А. Основы этой системы были предложены в 1901 г. Итальянским ученым Джорджи. Основными единицами системы МКСА являются метр, килограмм, секунда и ампер. Относительные и логарифмические величины и Единицы Относительная величина представляет собой безразмерное отношение физической величины к одноименной физической величине, принимаемой за исходную. Логарифмическая величина представляет собой логарифм (десятичный, Натуральный или при основании 2) безразмерного отношения двух одноименных физических величин.

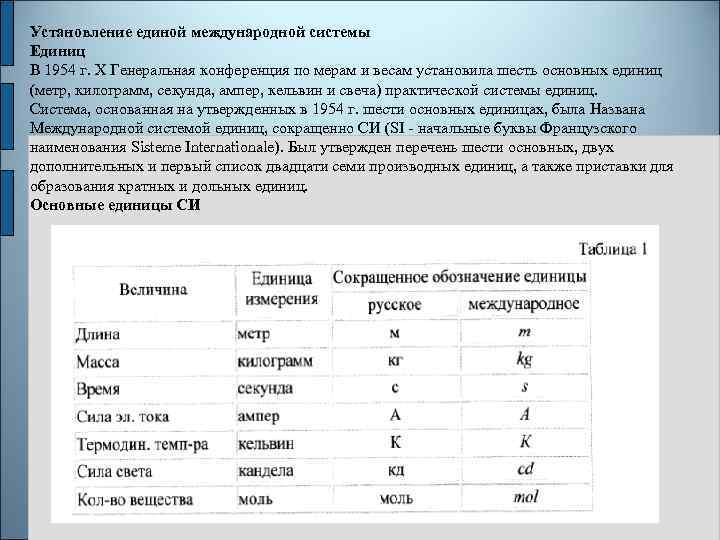Установление единой международной системы Единиц В 1954 г. X Генеральная конференция по мерам и весам установила шесть основных единиц (метр, килограмм, секунда, ампер, кельвин и свеча) практической системы единиц. Система, основанная на утвержденных в 1954 г. шести основных единицах, была Названа Международной системой единиц, сокращенно СИ (SI - начальные буквы Французского наименования Sisteme Internationale). Был утвержден перечень шести основных, двух дополнительных и первый список двадцати семи производных единиц, а также приставки для образования кратных и дольных единиц. Основные единицы СИ

Определения основных единиц, соответствующие решениям Генеральной конференции по мерам и весам, следующие: Метр равен длине пути, проходимого светом в вакууме за 1/299792458 долю секунды. Килограмм равен массе международного прототипа килограмма. Секунда равна 9192631770 периодам излучения, соответствующего переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133. Ампер равен силе неизменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малой площади кругового сечения, расположенным на расстоянии 1 м один от другого в вакууме, вызывает на каждом участке проводника длиной 1 м силу взаимодействия, равную 2 *10 -7 Н Кельвин равен 1/273. 16 части термодинамической температуры тройной точки воды. Моль равен количеству вещества системы, содержащей столько же структурных элементов, сколько содержится атомов в углероде- 12 массой 0. 012 кг. Кандела равна силе света в заданном направлении источника, испускающего монохроматическое излучение частотой 540 • 1012 Гц энергетическая сила света которого в этом направлении составляет 1/683 Вт/ср.

Дополнительные единицы СИ Единица плоского угла - радиан (рад) - угол между двумя радиусами окружности, дуга между которыми по длине равна радиусу. В градусном исчислении радиан равен 57° 17'48". Стерадиан (ср), принимаемый за единицу телесного угла, - телесный угол, вершина которого расположена в центре сферы и который вырезает на поверхности сферы площадь, равную площади квадрата со стороной, по длине равной радиусу сферы. Дополнительные единицы СИ использованы для образования единиц угловой скорости, углового ускорения и некоторых других величин. Сами по себе радиан и стерадиан применяются в основном для теоретических построений и расчетов, так как большинство важных для практики значений углов (полный угол, прямой угол и т. д. ) в радианах выражаются трансцендентными числами (2π , π/2 и т. д. ). Производные единицы СИ Производные единицы Международной системы единиц образуются с помощью простейших уравнений между величинами, в которых числовые коэффициенты равны единице

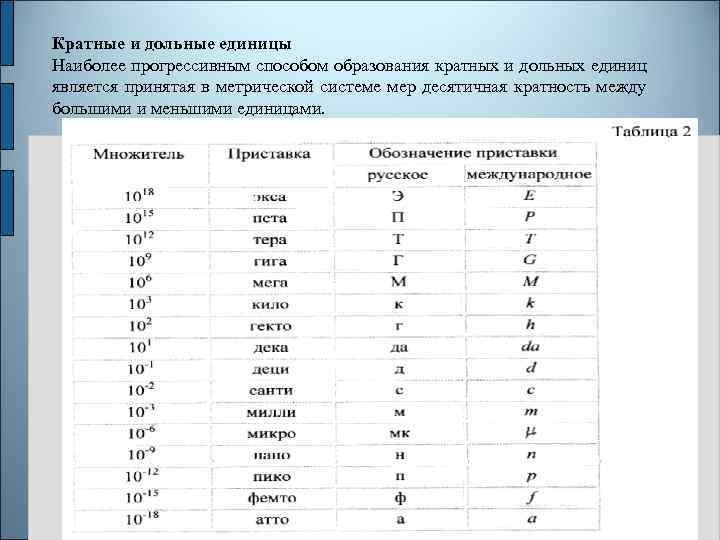Кратные и дольные единицы Наиболее прогрессивным способом образования кратных и дольных единиц является принятая в метрической системе мер десятичная кратность между большими и меньшими единицами.

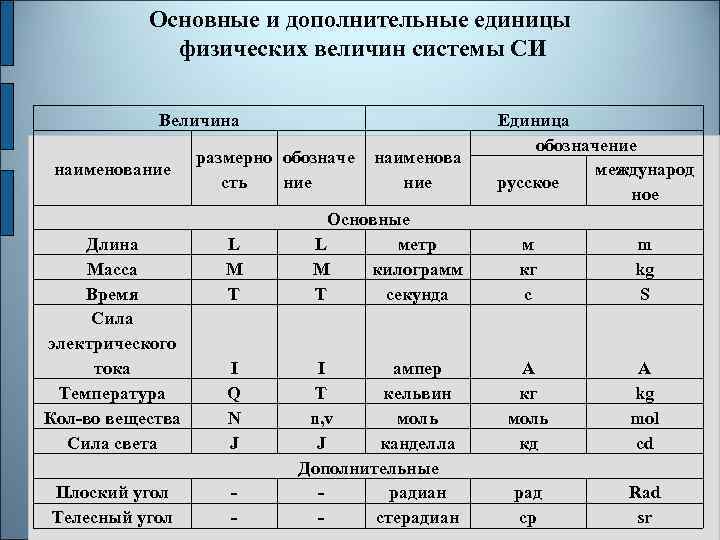Основные и дополнительные единицы физических величин системы СИ Величина наименование размерно обозначе сть ние Длина Масса Время Сила электрического тока Температура Кол-во вещества Сила света L M T Плоский угол Телесный угол - I Q N J наименова ние Основные L метр M килограмм T секунда I ампер T кельвин n, v моль J канделла Дополнительные радиан стерадиан Единица обозначение международ русское ное м кг с m kg S А кг моль кд A kg mol cd рад ср Rad sr

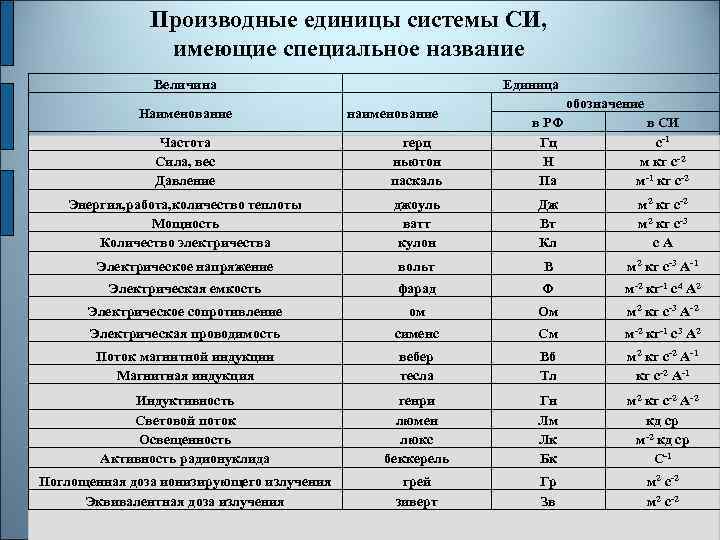Производные единицы системы СИ, имеющие специальное название Величина Наименование Единица наименование обозначение Частота Сила, вес Давление герц ньютон паскаль в РФ Гц Н Па в СИ с-1 м кг с-2 м-1 кг с-2 Энергия, работа, количество теплоты Мощность Количество электричества джоуль ватт кулон Дж Вт Кл м 2 кг с-2 м 2 кг с-3 с А Электрическое напряжение вольт В м 2 кг с-3 А-1 Электрическая емкость фарад Ф м-2 кг-1 с4 А 2 Электрическое сопротивление ом Ом м 2 кг с-3 А-2 Электрическая проводимость сименс См м-2 кг-1 с3 А 2 Поток магнитной индукции Магнитная индукция вебер тесла Вб Тл м 2 кг с-2 А-1 Индуктивность Световой поток Освещенность Активность радионуклида генри люмен люкс беккерель Гн Лм Лк Бк м 2 кг с-2 А-2 кд ср м С-1 Поглощенная доза ионизирующего излучения Эквивалентная доза излучения грей зиверт Гр Зв м 2 с-2

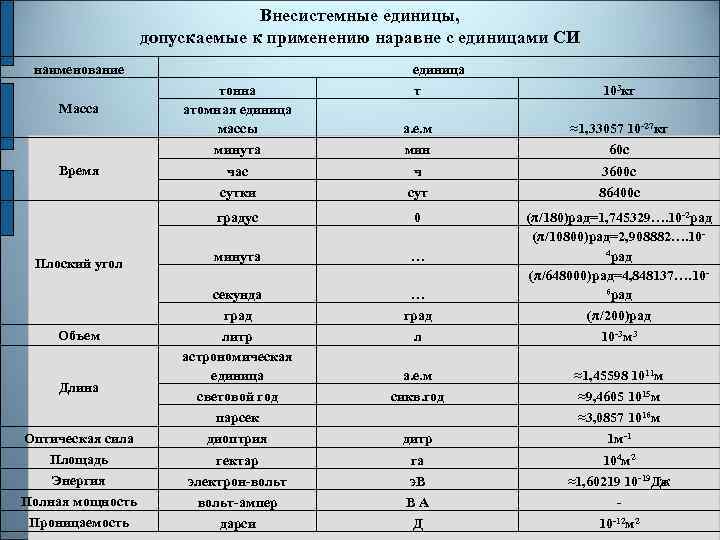Внесистемные единицы, допускаемые к применению наравне с единицами СИ наименование единица тонна атомная единица массы т 103 кг а. е. м ≈1, 33057 10 -27 кг минута мин 60 с час ч 3600 с сутки сут 86400 с градус 0 минута … секунда … (π/180)рад=1, 745329…. 10 -2 рад (π/10800)рад=2, 908882…. 104 рад (π/648000)рад=4, 848137…. 106 рад град (π/200)рад литр астрономическая единица л 10 -3 м 3 а. е. м ≈1, 45598 1011 м световой год сикв. год ≈9, 4605 1015 м парсек ≈3, 0857 1016 м Оптическая сила диоптрия дитр 1 м-1 Площадь гектар га 104 м 2 Энергия электрон-вольт э. В ≈1, 60219 10 -19 Дж Полная мощность вольт-ампер В А - Проницаемость дарси Д 10 -12 м 2 Масса Время Плоский угол Объем Длина

Соотношение между внесистемными единицами системы СИ Величина Соотношение единиц Работа, энергия 1 кг с м=9, 81 Дж 1 Вт ч=3, 6*103 Дж 1 э. В=1, 6*10 -19 Дж Давление 1 кгс/см 2=9, 81*104 Па 1 мм рт. ст=133 Па 1 бар=105 Па 1 атм=1, 01*105 Па 1 кгс/мм 2=9, 81*106 Па Частота вращения 1 об/с=1 с-1*1 об/мин=1/60 с-1 Количество теплоты 1 ккал=4, 19*103 Дж Вязкость 1 с. Пз=1 м. Па с=1*10 -3 Па с

Соотношение между внесистемными единицами системы СИ Величина Длина Время Плоский угол Объем, вместимость Масса Сила Работа, энергия Мощность Давление Напряжение (механическое) Частота вращения Количество теплоты Соотношение единиц 1 ангстрем (А)=10 -10 м=10 -8 см 1 сут=86400 с 1 год=365, 25 сут=3, 16*107 с 10=π/180 рад=1, 75*10 -2 рад 1'=π/108*10 -2 рад=2, 91*10 -4 рад 1''=π/648*10 -3 рад=4, 85*10 -6 рад 1 л=10 -3 м 3=103 см 3=10 дм 3 1 т=103 кг=106 г 1 а. е. м. =1, 66*10 -27 кг 1 кгс=9, 81 Н 1 кг с м=9, 81 Дж 1 Вт ч=3, 6*103 Дж 1 э. В=1, 6*10 -19 Дж 1 л. С. =736 Вт 1 кгс/см 2=9, 81*104 Па 1 мм рт. ст. =133 Па 1 бар=105 Па 1 атм=1, 01*105 Па 1 кгс/мм 2=9, 81*106 Па 1 об/с=1 с-1 1 об/мин=1/60 с-1 1 кал=4, 19 Дж 1 ккал=4, 19*103 Дж

Н. А. Корфу принадлежит инициатива проведения учительских съездов. Он провёл два съезда учителей Александровского уезда и описал их. Этот опыт был подхвачен в других земствах, а 1872 г. в Москве состоялся 1 -й Всероссийский учительский съезд. Работа съездов включала чтение лекций, доклады учителей и обсуждение их опыта работы, проведение открытых уроков. При каждом съезде работала специально организованная на время съезда школа, в которой проводились и обсуждались показательные уроки. Кроме съездов, стали проводиться учительские курсы, более длительные по времени, ориентированные на систематическое обучение и повышение квалификации учителей.

Идея повышения эффективности образования на селе получила развитие в педагогической деятельности Н. Ф. Бунакова. Николай Федорович — педагог, разделявший принципы органической связи школьного дела с народной жизнью, внимания к ученику и доверия к личности и труду народного учителя. Н. Ф. Бунаков указывал, что важнейшим условием успешной работы сельской школы является заинтересованность в ней местного населения, открытость школы для контроля крестьянской общиной: «…Те, кто доверяет училищу своих детей, неужели не вправе спросить: что же вы сделали с нашими детьми? Как и чему их учили? » . Им была обоснована и проверена на практике необходимость взаимодействия сельской школы с социальным окружением.

Огромную роль в развитии образования на селе сыграла педагогическая деятельность выдающегося русского писателя и мыслителя Л. Н. Толстого. Лев Николаевич сформулировал цели народной школы: воспитание творческой, нравственной личности, формирование в процессе обучения творческого мышления и нравственного самосознания, научность полученного образования. В статье «О народном образовании» он выступает за адаптивный характер образования сельских детей, указывая, что ученик должен иметь право выбрать то образование, которое ему подходит, или «…уклониться от того образования, которое по инстинкту не удовлетворяет его…» (185).

В конце XIX — начале XX в. в ряде сельских школ Смоленской губернии осуществлялась инновационная деятельность под руководством профессора Московского университета, члена-корреспондента Российской академии наук С. А. Рачинского. Как отмечает Ю. В. Василькова и Т. А. Василькова, «в школе Рачинского была сделана попытка объединить религиозное, нравственное, трудовое и профессиональное воспитание, обучение, согласованное с потребностями крестьянской семьи и сельской общины. Он впервые в отечественной педагогике выявил специфические условия образования в сельской местности и возможности эффективного осуществления образовательного процесса с учётом этих условий (139). С. А. Рачинский считал, что сельская школа не должна существовать в отрыве от социального окружения. Он создал оригинальную систему подготовки учителей в самой школе, воспитав ряд педагогов-новаторов.

Русские педагоги К. Д. Ушинский, Н. Ф. Бунаков, Н. А. Корф, В. И. Водовозов, В. П. Вахтеров выступали за новую демократическую народную школу, дающую подрастающему поколению научное и связанное с жизнью полноценное общее образование; выдвигали на первый план воспитательные задачи с целью подготовить всесторонне образованного и деятельного человека и повышение квалификации учителей. В деле народного образования перед земским самоуправлением было поставлено несколько задач, которые оно пыталось решить с разной степенью успеха на всем протяжении своего существования: 1. Доступность образования; 2. Кадровое обеспечение; . 3. Широкая просветительская работа в рамках внешкольного образования; . 4. Социальная защита учительства; 5. Социализирование педагогики ; 6. Развитие общественной педагогической мысли.

ПЕРСПЕКТИВЫ РАЗВИТИЯ УЧАСТИЯ ИНСТИТУТОВ ГРАЖДАНСКОГО ОБЩЕСТВА И ШИРОКОЙ ОБЩЕСТВЕННОСТИ В ОБРАЗОВАНИИ На современном этапе в России существуют разные стратегии взаимоотношения государства и общества в управлении системой образования: первая стратегия – либерально-гуманистическая – предлагает максимально индивидуализировать образование, подчинив его задачам удовлетворения запросов конкретной личности и обеспеченных групп населения за счет предоставления дополнительных платных образовательных услуг. вторая – охранительно-государственная – настаивает на максимальном сохранении высокого уровня общего среднего массового образования с опорой на единые для всех образовательные стандарты. третья – социокультурного развития – предполагает при безусловной поддержке существующего уровня общего среднего образования, как важнейшего условия развития современных форм организации труда, поддержку инновационных проектов и образовательных инициатив, обеспечивающих прорыв к новому общественному укладу в России.

Проблемы развития общественного участия в образовании связаны с парадигмальными особенностями взаимоотношенй государства и образования в России. В этой связи значительно актуализировался исследовательский интерес к отечественному опыту внедрения общественной составляющей в систему народного образования, нокопленному в земской школе во второй половине XIX- начале XX вв. Федеральный закон «Об образовании» сформулировал одним из принципов государственной политики в области образования демократический, государственно-общественный характер управления (ст. 2, п. 6. ) В системе образования необходимо обеспечить: Во-первых, открытость образования; Во-вторых, переход от патерналистской модели к модели взаимной ответственности, к усилению роли всех субъектов образовательной политики и их взаимодействия.

Управление образовательными системами должно строиться на принципах открытого общества таких, как: • создание и поддержка более открытого управления образованием; • реструктуризация моделей управления и расширение их возможностей; • пропаганда демократических подходов, терпимости и уважения других точек зрения; • более глубокое вовлечение образовательного и местного сообщества в процесс принятия решений.

Чтобы быть услышанной и получить реальную возможность влиять на образование и управление образованием, общественность должна быть определенным образом структурированной, организованной, способной выступать в качестве субъекта равноправного диалога с государством и профессионалами от образования.

В современном мире общей тенденцией является поощрение инициативы «с мест» при сохранении единого правового пространства. В Тюменской области накоплен опыт взаимодействия образовательных учреждений и общественности. Формами государственно-общественного управления являются родительские комитеты школ, советы образовательных учреждений, попечительские советы и др. Работа «круглого стола» «Модели органов государственно-общественного управления в сельских образовательных учреждениях» с участием специалистов органов управления образованием, педагогов, общественности и координаторов проекта НФПК

Становление действительно «демократического, государственно-общественного характера управления» требует создания четких правовых и организационных условий.

Новым органом государственно-общественного управления образованием стал Управляющий совет – орган прямого общественного участия в управлении школой, способный воплотить в жизнь важнейший принцип государственной политики в сфере образования – демократический, государственно-общественный характер управления.

В Тюменской области имеется распоряжение Правительства Тюменской области № 891 от 7 ноября 2005 г. , утвердившее Примерное положение об Управляющем совете общеобразовательного учреждения. Данный нормативный правовой акт определил основные задачи, принципы деятельности Управляющего совета, общий порядок выборов, кооптации и назначения членов УС. Примерный состав Управляющего Совета

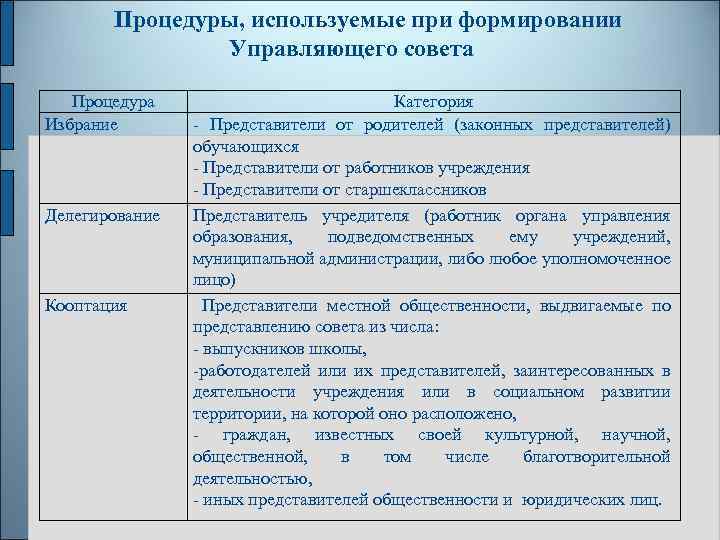Процедуры, используемые при формировании Управляющего совета Процедура Избрание Делегирование Кооптация Категория - Представители от родителей (законных представителей) обучающихся - Представители от работников учреждения - Представители от старшеклассников Представитель учредителя (работник органа управления образования, подведомственных ему учреждений, муниципальной администрации, либо любое уполномоченное лицо) Представители местной общественности, выдвигаемые по представлению совета из числа: - выпускников школы, -работодателей или их представителей, заинтересованных в деятельности учреждения или в социальном развитии территории, на которой оно расположено, - граждан, известных своей культурной, научной, общественной, в том числе благотворительной деятельностью, - иных представителей общественности и юридических лиц.

Из опыта работы Управляющих советов школ Тюменской области 1. Управляющий совет гимназии № 49 г. Тюмени, директор Лохман Н. П. Высшим органом самоуправления Гимназии является Конференция представителей трех основных категорий ее членов: учителей Гимназии, обучающихся и их родителей (законных представителей). Конференция утверждает Управляющий совет Гимназии. В состав Совета входят педагоги (избираются на Педагогическом совете), родители (законные представители), которые избираются на общешкольном родительском собрании и обучающиеся третьей ступени обучения (избираются на общем собрании учащихся). В состав Совета входит по должности директор Гимназии, могут быть кооптированы представители общественности по представлению Учредителя или избранных членов Совета. 2. Из опыта работы Управляющего совета МОУ СОШ № 7 г. Тобольска Члены Управляющего совета из числа родителей избираются на конференции. Делегаты конференции избираются на классных родительских собраниях по одному от каждого класса. На педагогическом совете школы избираются представители из числа педагогов. На основании приказа Комитета по образованию в состав Управляющего совета входит представитель учредителя. В соответствии с Уставом школы в состав Управляющего совета с правом совещательного голоса входит представитель ВУЗа, с которым мы сотрудничаем на основе трехстороннего договора.

3. Управляющий совет сельской школы Слобода-Бешкильская СОШ Исетского района, директор Моржова С. В. Коллектив Слобода-Бешкильской средней школы рассматривает Управляющий совет как один из важных элементов института гражданского общества, обеспечивающий соблюдение прав человека, создающий условия для приобретения опыта демократического поведения. Авторитетность Управляющего совета нашей школы обеспечивается его составом: родители, педагоги, сотрудники школы, учащиеся 9, 10, 11 классов, представители учредителя, представитель администрации села, староста церкви, директор дома культуры, председатель совета ветеранов, заведующая сельской библиотекой, заведующая ФАПом, старший воспитатель детского сада. Из проведенных примеров можно сделать некоторые выводы о том, эффективно организованная деятельность управляющего совета - это мощная социальная защита для всех работников школы, а также дополнительный организационный, финансовый и интеллектуальный ресурс развития школы. .

ЗАКЛЮЧЕНИЕ Историография вопросов местного самоуправления и общественного участия в образовании насчитывает около 150 лет. Прежние принципы построения системы управления народным образованием укладывались в действовавшие в разные периоды истории институциональные парадигмы. Этот тезис, по нашему мнению, применим, как к земской школе XIX – начала XX в. , с ее динамичной историей взаимодействия государства и общества и с постепенно развивающимися полномочиями общественного участия, так и к советской школе с ее раз и навсегда закрепленными полномочиями государственных органов и нишей общественных и профессиональных организаций. В настоящее время школа переживает новый бум, связанный с реформами местного самоуправления и самой системы образования.

Как показывают многочисленные источники, обширный опыт привлечения общественности к участию в управлении на уровне местного самоуправления, учитывающий национальную и культурную специфику, а также государственную политику, был накоплен в нашей стране на протяжении второй половины XIX – начала XX в. Наиболее благоприятные условия для проявления инициативы группами общественности создаются в демократических общественных системах, основанных на принципах гуманистического мировоззрения. .

Благодарю уважаемую комиссию за внимание и выражаю мою искреннюю признательность Людмиле Павловне Беловой за чуткое руководство.