Precedence Constrained Scheduling Abhiram Ranade Dept of CSE

Precedence Constrained Scheduling Abhiram Ranade Dept. of CSE IIT Bombay

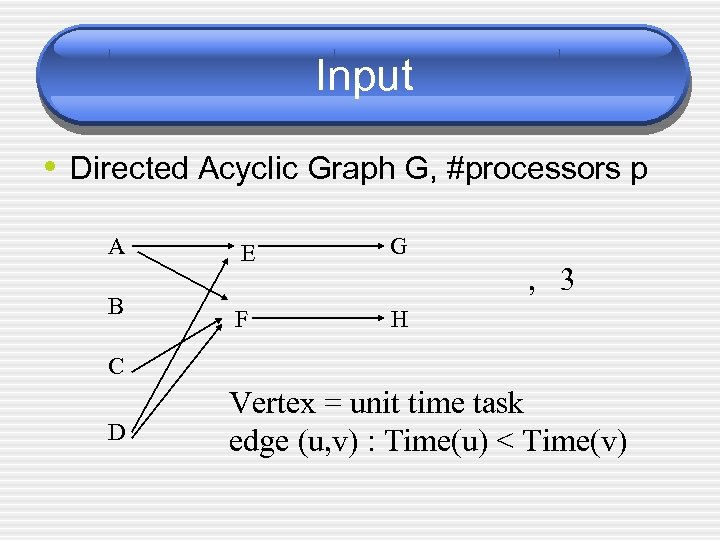
Input • Directed Acyclic Graph G, #processors p A B E G F H , 3 C D Vertex = unit time task edge (u, v) : Time(u) < Time(v)

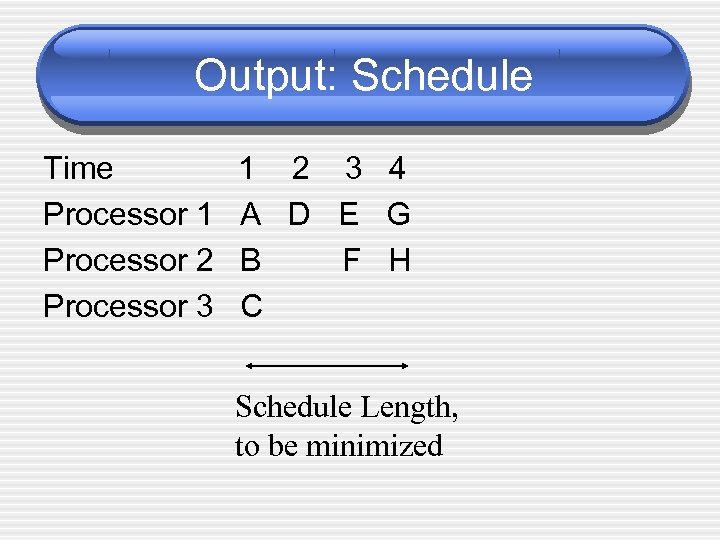
Output: Schedule Time Processor 1 Processor 2 Processor 3 1 2 3 4 A D E G B F H C Schedule Length, to be minimized

Applications • Project management. Vertex = lay • • foundation, build walls. Edges: what happens first to what happens later. Processors : Number of workmen. MS Project, others. Our problem: Simplified version. Other applications: Parallel computing.

Summary of results • • Polytime algorithm when p=2. [Fuiji. . 69] NP-hard for variable p. [Len. Kan 78] NP-hardness not known for fixed p > 2. Polytime algorithm for trees. [Hu 61]

Summary of results - 2 • Any greedy algorithm gives 2 - 1/p • • • approximation. i. e. Schedule of length at most (2 - 1/p) times Optimal length. [Coffman-Graham 72, Lam-Sethi 77] give 2 - 2/p approximation algorithm. [Gangal-Ranade 08] give 2 – 7/(3 p+1) approximation for p > 3. [Svensson 10] Better than 2 -ε unlikely.

Outline • Elementary Lower Bound ideas • Elementary algorithm and analysis • Deadline Constraints [Gar. Joh 76] § More complex problem, but generates new ideas. § 2 processor optimality, also without deadlines § Essentially gives 2 - 2/p approximation • Ideas behind 2 - 7/(3 p+1) approximation algorithm

Elementary Lower Bounds • To prove optimality of any algorithm, need • • to show why it cannot be improved, i. e. lower bound on schedule length. OPT H = Length of longest path in G. OPT [ N / p ], N = #nodes [ x ] = ceiling(x), smallest integer x. Example: H = 3, [N/p] =[8/3] = 3

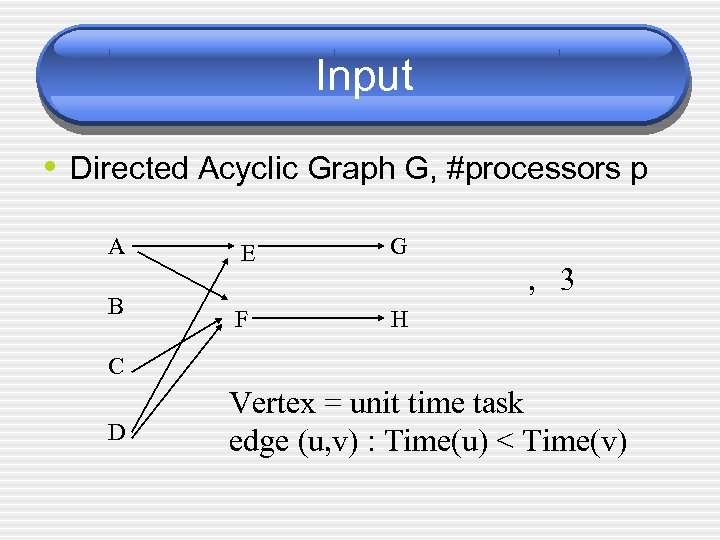
Input • Directed Acyclic Graph G, #processors p A B E G F H , 3 C D Vertex = unit time task edge (u, v) : Time(u) < Time(v)

Generic Algorithm 1. Pick any “ready” vertex. 2. Schedule it at earliest possible time. 3. Repeat until done. ready = no predecessors yet unscheduled. earliest possible = after predecessors.

Proof of 2 approximation • Full (time) slot: All processors busy • Number of “full” slots N/p • Number of partial slots H. Why? § Partial slot: Some processor did not get work. § All maximally long paths must shrink. § This can happen only H times. • Time N/P + H OPT + OPT = 2 OPT • Improve to 2 - 1/p.

Deadline Constraints [Gar. Joh 76] • Additional Input: D(v) : time by which v • must be processed. Need a schedule with p processors in which precedence constraints and deadlines are respected.

Deadline Propagation • v has N(d) descendants with deadline d v must itself finish by d - [N(d)/p]. new deadline: d(v) = min( D(v), mind d -[N(d)/p] ) • In what order to calculate? • (u, v) edge d(u) < d(v) • GJ Algo: priority = deadline. Optimal for p=2!

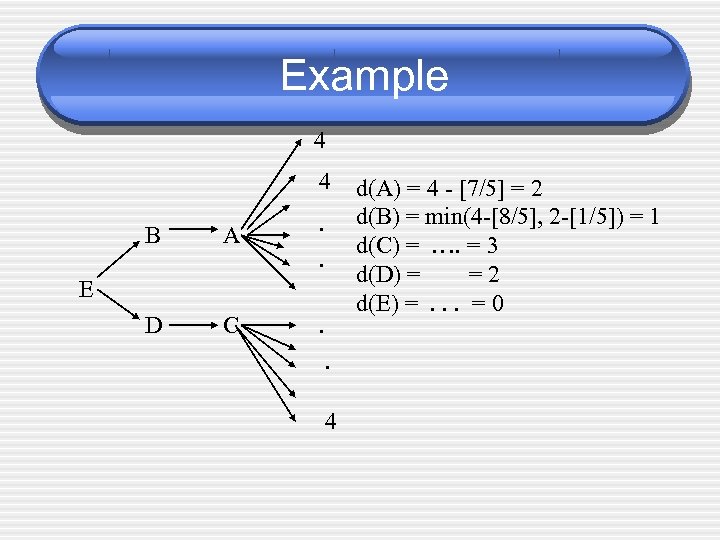
Example 4 4 B A . . D C . E. 4 d(A) = 4 - [7/5] = 2 d(B) = min(4 -[8/5], 2 -[1/5]) = 1 d(C) = …. = 3 d(D) = =2 d(E) =. . . = 0

GJ Deadline Properties • Deadline < 1 : schedule not possible. • Optimal Schedule length • • Max deadline - Min deadline + 1. Opt for example 4 - 0 + 1 = 5 Load bound : [N/p] = [17/5] = 4 Longest path: H = 4 Is this the best lower bound?

Partial Slot Bound • Max Deadline – Min Deadline + 1 >= H Time 1 2. . . t. . . P 1 uv P 2 u is ancestor of v, so d(u) < d(v)

Load Bound • Max deadline – Min deadline + 1 >= [N/p] • Add a universal parent z • d(z) <= Max deadline – [Number of • • descendants with deadline d/p] = Max – [N/p] Min deadline <= Max – [N/p]

Scheduling without deadlines • Set d(terminal vertices) = k, some number. • Propagate deadlines. m = least deadline. • Schedule from time m using deadlines. Theorem: Algorithm is optimal for p=2.

2 Processor Optimality • v : earliest scheduled vertex not meeting • deadline w : latest scheduled vertex before v scheduled alone. Always exists? Time: 1 2 3 Proc 1: Proc 2: t’ w - t v Nodes in region must be Descendants of w. Region has 2(t-t’)-1 nodes with Deadline t-1. • d(w) t’, d(v) t-1 d(w) t-1 - (2(t-t’)-1)/2 = t’-1 Contradiction

Remarks • Why does this not work for p > 2? • Algorithm gives 2 - 2/p approximation for even p. More complex proof.

Improvements to GJ [GR 09] • Node v has N(d, L) descendants at • distance at least L+1 having deadline at least d Then d(v) mind, L d - L - [N(d, L)/p]

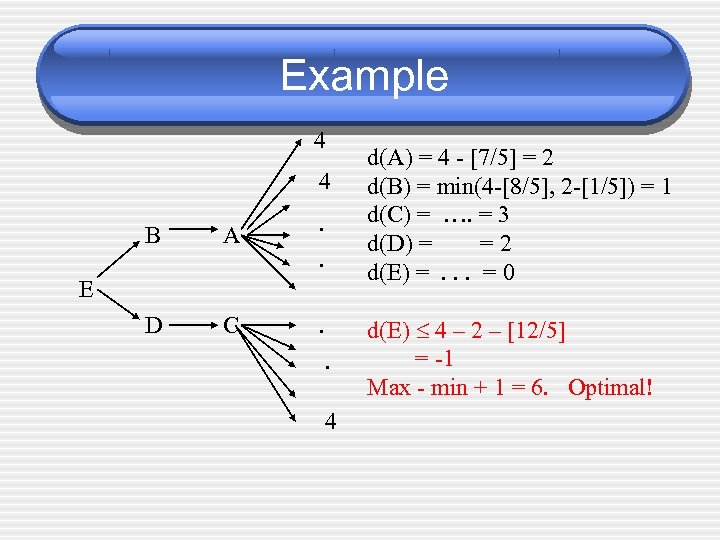
Example 4 4 B A . . D C . E. 4 d(A) = 4 - [7/5] = 2 d(B) = min(4 -[8/5], 2 -[1/5]) = 1 d(C) = …. = 3 d(D) = =2 d(E) =. . . = 0 d(E) 4 – 2 – [12/5] = -1 Max - min + 1 = 6. Optimal!

Algorithm • Set d(terminal vertices) = 0 • Propagate deadlines. New rule. • For each v in non-decreasing deadline order: § (Rearrange ancestors of v if possible). § Schedule v in earliest possible slot, and smallest numbered processor.

Rearrange ancestors of v • Suppose t = last slot with ancestors of v. • Suppose vertices in slots t-1, t have • • • same deadline. Suppose v has < p ancestors in t-1, t. Then move ancestors of v to slot t-1, move other vertices to slot t. If slot t is not full, v can be scheduled in t.

Analysis Outline • Key part of proof: If algorithm constructs a • • long schedule, then deadline must drop a lot moving from last column to first. Max deadline - min deadline + 1 optimal schedule length. Optimal schedule must also be long, so good approximation factor.

How deadline varies in the schedule Time> 1 2 3 …. 1 2 3. . p uv w Deadline can only increase in first row: D(u) D(v) Deadline can only increase in any column: D(u) D(w)

Partial slot rule 1 2 3. . p 1 2 3 …. increasing time. uv w x y - Deadline must increase in first row after a partial slot: D(u) < D(v) … why was not v scheduled earlier?

1 -slot rule 1 2 3. . p 1 2 3 …. increasing time. u - v Let M denote the number of nodes scheduled after u. Then D(u) D(v) - [M/p]

Intuition: Easy schedules • Suppose all slots are partial: drop per slot. • Thus total deadline drop = length of • • • schedule. Optimal! Suppose all slots are either 1 slots or full slots. 1 -slot rule gives optimality.

Intuition: Difficult Schedules • Schedules with mixture of 2 -slots and full • • slots. Extreme case 1: 2 -slots at the beginning, full slots at the end. Extreme case 2: 2 slots and full slots alternate.

Extreme case 1: • • • Time> <--L--> <---m--> P 1 : a v v v v v w P 2 : b v v v v v P 3 : vvvvv P 4 : vvvvv • • A, b must be ancestors of all to right. One of them say a, must be ancestor of mp/2 d(a) d(w) - L - mp/2. Drop = #2 slots + full slots/2

Extreme Case 2 • • • Time: 1 P 1 : v P 2 : v P 3 : P 4 : 2 3 4 5. . v v v v • Use ancestor rearrangement to argue large drop.

Actual Analysis • Keep track of how many 1 -slots, 2 -slots, • • full slots. . encountered. Relate numbers to deadline drop, schedule length. Solve for schedule length/deadline drop.

Remarks • Analysis is complicated, but not much • • more than 2 -2/p analysis of Lam-Sethi. Algorithm is simpler than Coffman-Graham. Technique will not work beyond 2 - 3/p. Even getting there is hard.