МПГУ Операции математической логики1.ppt
- Количество слайдов: 48

Правительство Москвы Московский департамент образования ГОУ ВПО МГПУ ОУК естественнонаучных дисциплин Операции математической логики Москва 2008

Содержание • • • Отрицание Конъюнкция Дизъюнкция Импликация Эквиваленция Сложение по модулю 2 (Исключающее ИЛИ) • Штрих Шеффера (И -НЕ)

Содержание(прод. ) • Стрелка Пирса (ИЛИ -НЕ) • Запрет по В • Запрет по А • Элементарная конъюнкция • Дизъюнктивная нормальная форма (ДНФ) • Аналитическое представление табличнозаданной функции

Содержание(прод. ) • Элементарная дизъюнкция • Конъюнктивная нормальная форма (КНФ) • Аналитическое представление табличнозаданной функции • Решение логических задач • Сложные функции
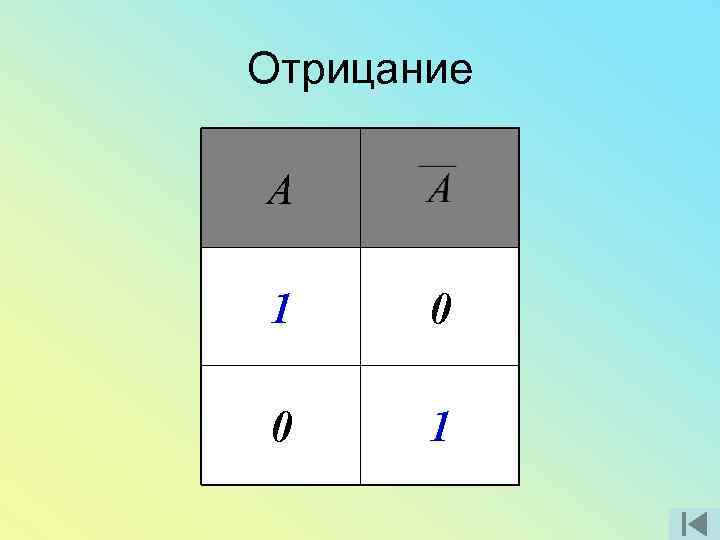
Отрицание А 1 0 0 1
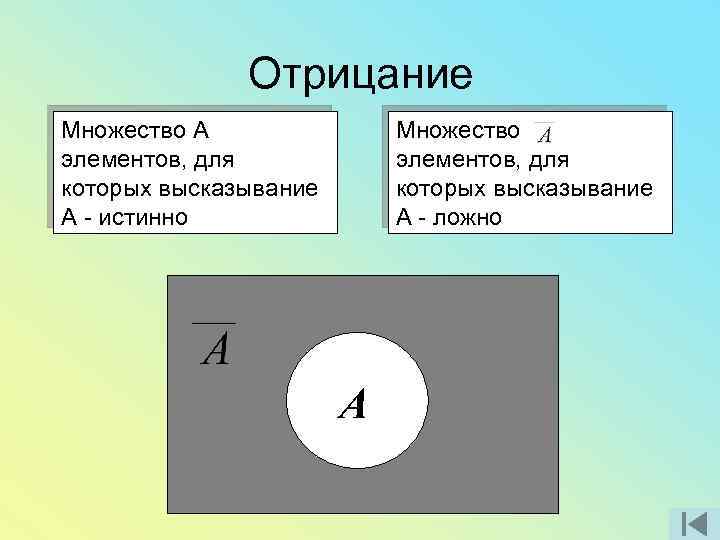
Отрицание Множество А элементов, для которых высказывание А - истинно Множество элементов, для которых высказывание А - ложно А

Конъюнкция А 0 0 1 1 В 0 1 0 0 0 1
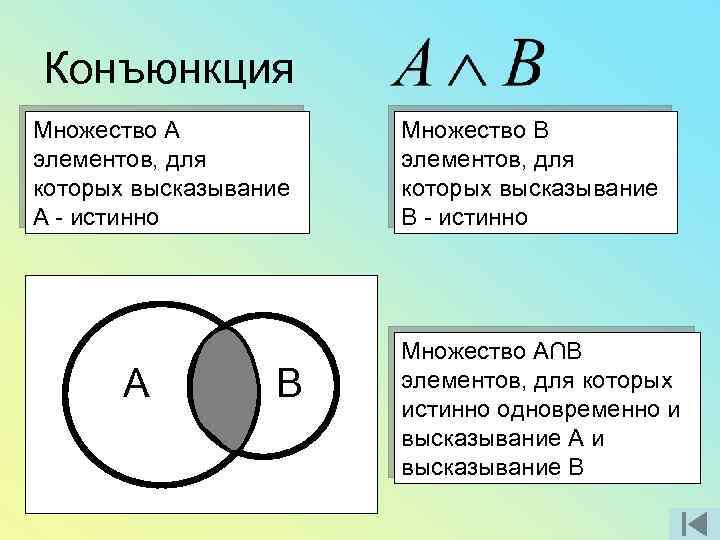
Конъюнкция Множество А элементов, для которых высказывание А - истинно А В Множество В элементов, для которых высказывание В - истинно Множество А∩В элементов, для которых истинно одновременно и высказывание А и высказывание В
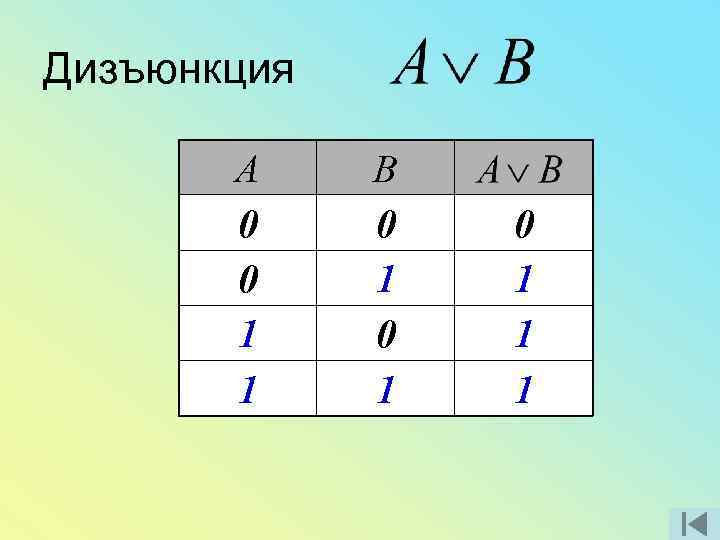
Дизъюнкция А 0 0 1 1 В 0 1 0 1 1 1
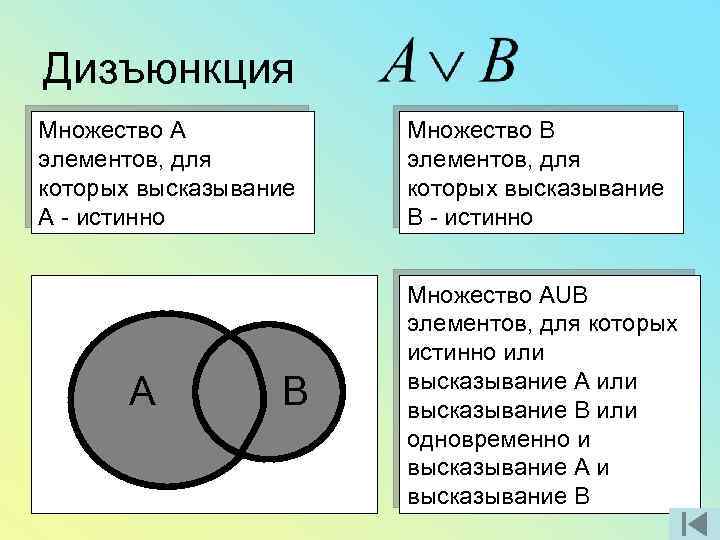
Дизъюнкция Множество А элементов, для которых высказывание А - истинно А В Множество В элементов, для которых высказывание В - истинно Множество АUВ элементов, для которых истинно или высказывание А или высказывание В или одновременно и высказывание А и высказывание В
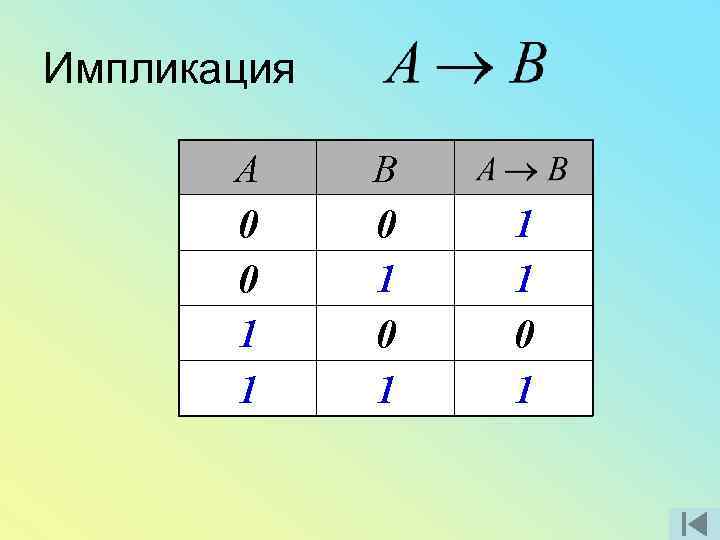
Импликация А 0 0 1 1 В 0 1 1 1 0 1
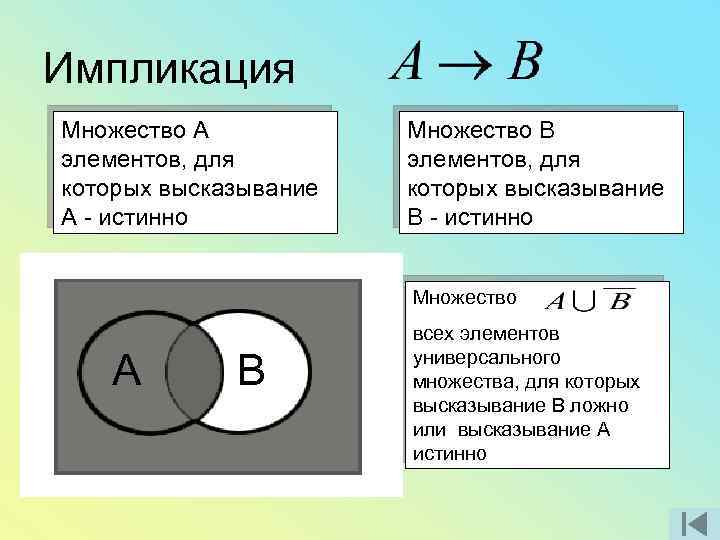
Импликация Множество А элементов, для которых высказывание А - истинно Множество В элементов, для которых высказывание В - истинно Множество А В всех элементов универсального множества, для которых высказывание В ложно или высказывание А истинно
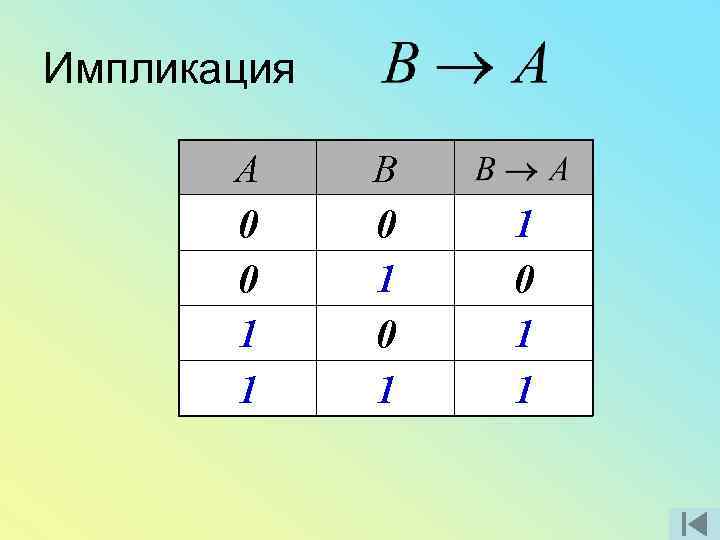
Импликация А 0 0 1 1 В 0 1 1
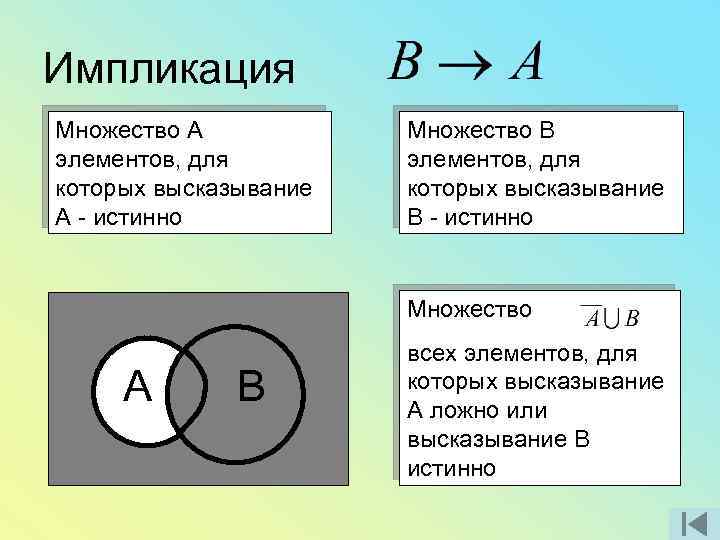
Импликация Множество А элементов, для которых высказывание А - истинно Множество В элементов, для которых высказывание В - истинно Множество А В всех элементов, для которых высказывание А ложно или высказывание В истинно
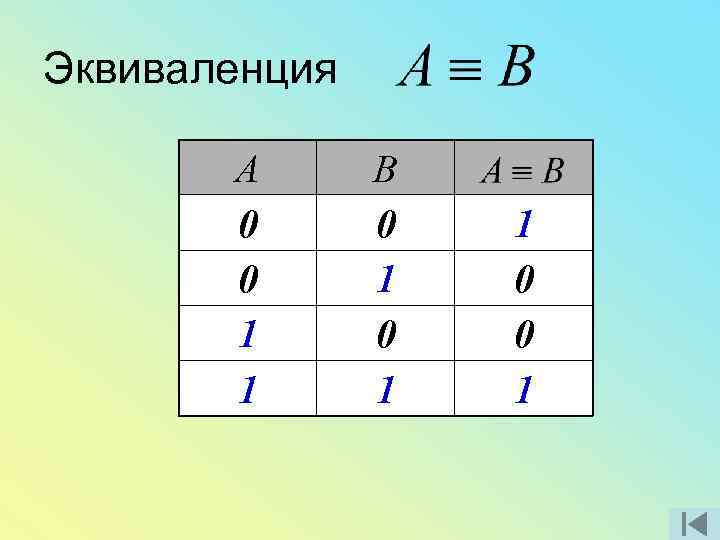
Эквиваленция А 0 0 1 1 В 0 1 1 0 0 1
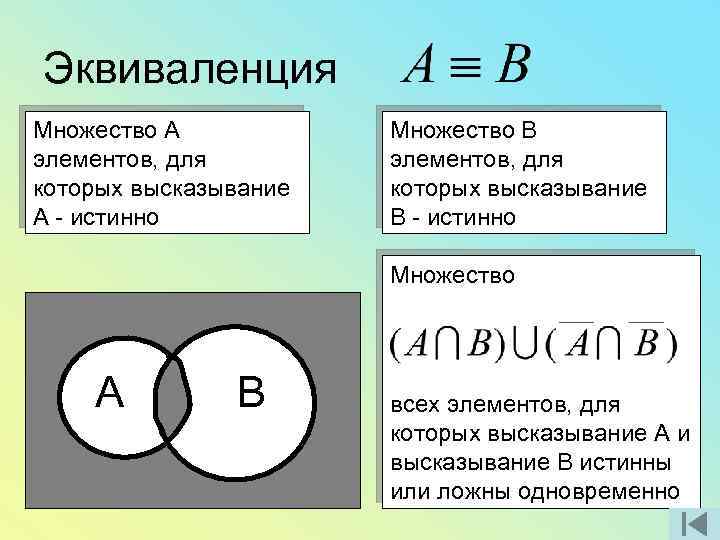
Эквиваленция Множество А элементов, для которых высказывание А - истинно Множество В элементов, для которых высказывание В - истинно Множество А В всех элементов, для которых высказывание А и высказывание В истинны или ложны одновременно
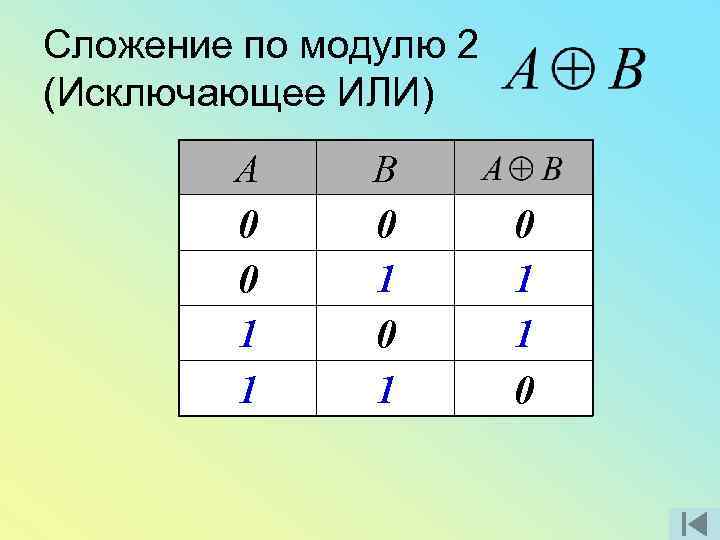
Сложение по модулю 2 (Исключающее ИЛИ) А 0 0 1 1 В 0 1 0 1 1 0

Сложение по модулю 2 (Исключающее ИЛИ) Множество А элементов, для которых высказывание А - истинно Множество В элементов, для которых высказывание В - истинно Множество А В всех элементов, для которых истинно высказывание А или истинно высказывание В но не оба одновременно.

Штрих Шеффера (И -НЕ) А 0 0 1 1 В 0 1 1 1 1 0
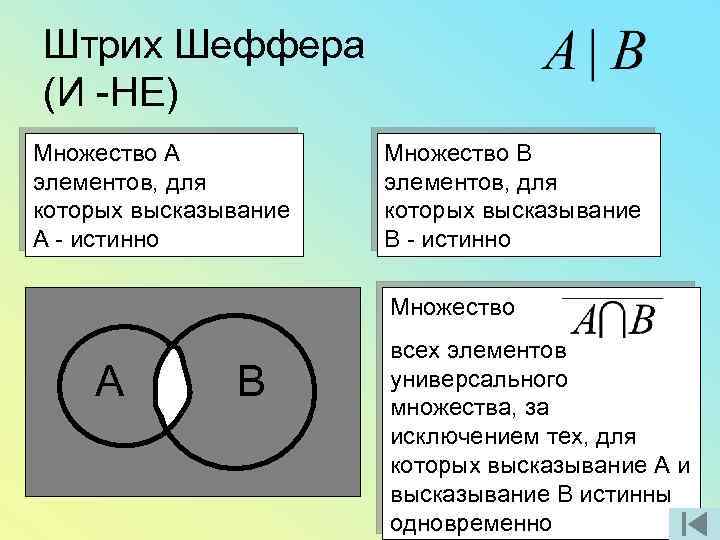
Штрих Шеффера (И -НЕ) Множество А элементов, для которых высказывание А - истинно Множество В элементов, для которых высказывание В - истинно Множество А В всех элементов универсального множества, за исключением тех, для которых высказывание А и высказывание В истинны одновременно
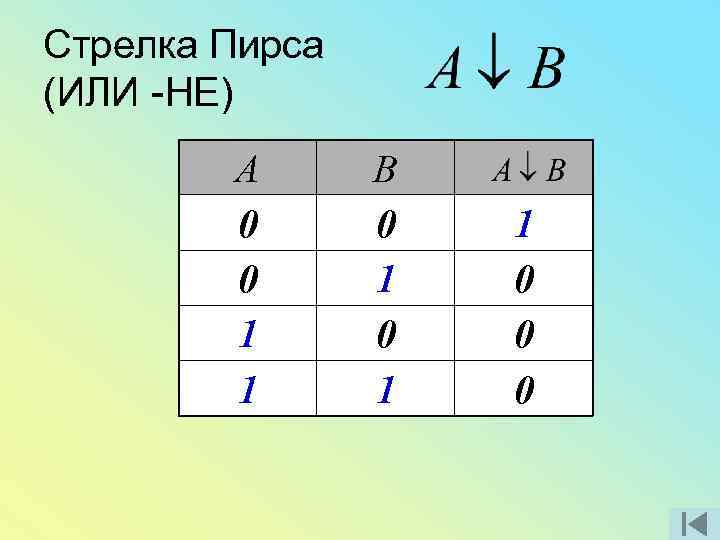
Стрелка Пирса (ИЛИ -НЕ) А 0 0 1 1 В 0 1 1 0 0 0
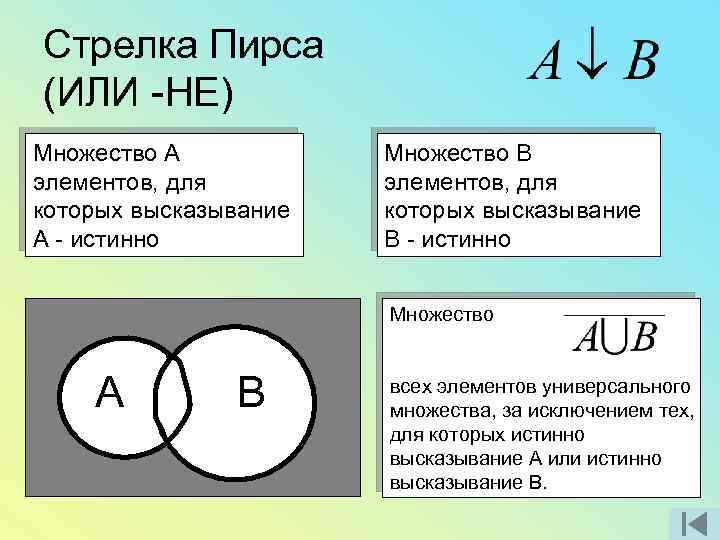
Стрелка Пирса (ИЛИ -НЕ) Множество А элементов, для которых высказывание А - истинно Множество В элементов, для которых высказывание В - истинно Множество А В всех элементов универсального множества, за исключением тех, для которых истинно высказывание А или истинно высказывание В.

Запрет по В А 0 0 1 1 В 0 1 0

Запрет по В Множество А элементов, для которых высказывание А - истинно Множество В элементов, для которых высказывание В - истинно Множество А В всех элементов, для которых истинно высказывание А за исключением тех, для которых истинно высказывание В.
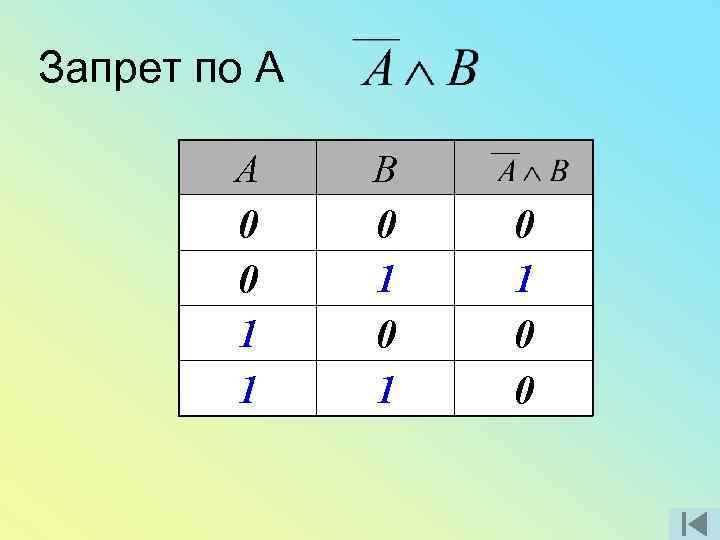
Запрет по А А 0 0 1 1 В 0 1 0 1 0 0
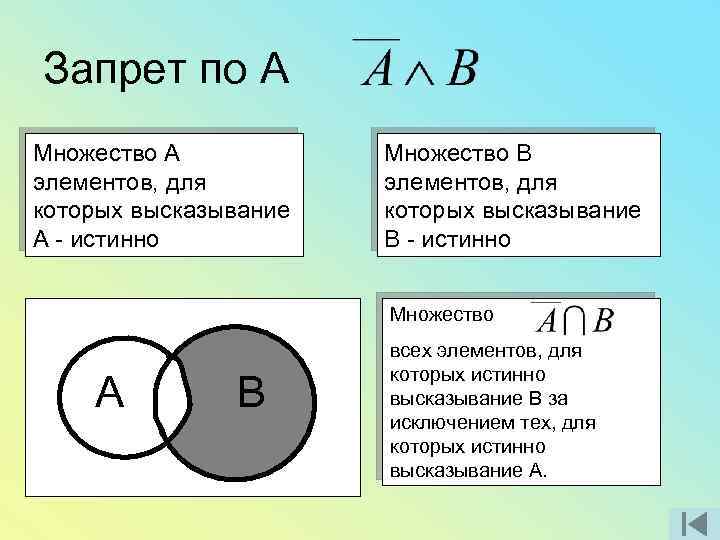
Запрет по А Множество А элементов, для которых высказывание А - истинно Множество В элементов, для которых высказывание В - истинно Множество А В всех элементов, для которых истинно высказывание В за исключением тех, для которых истинно высказывание А.
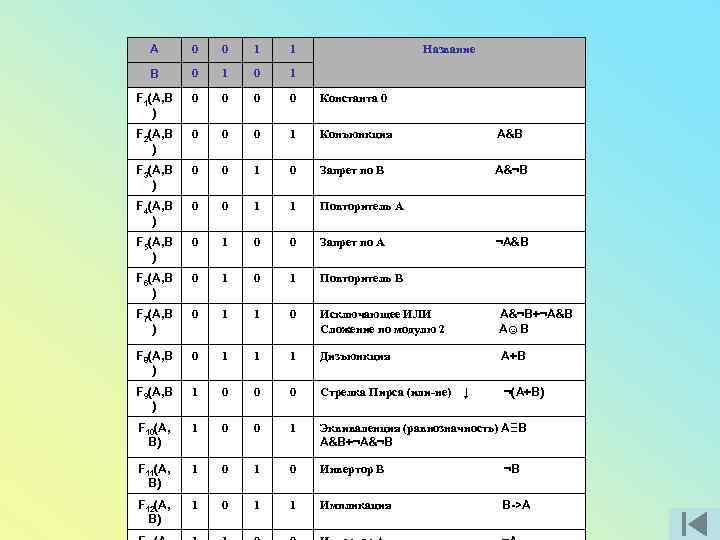
A 0 0 1 1 B 0 1 F 1(A, B ) 0 0 Константа 0 F 2(A, B ) 0 0 0 1 Конъюнкция A&B F 3(A, B ) 0 0 1 0 Запрет по B A&¬B F 4(A, B ) 0 0 1 1 Повторитель А F 5(A, B ) 0 1 0 0 Запрет по А F 6(A, B ) 0 1 Повторитель В F 7(A, B ) 0 1 1 0 Исключающее ИЛИ Сложение по модулю 2 A&¬B+¬A&B А☺В F 8(A, B ) 0 1 1 1 Дизъюнкция А+В F 9(A, B ) 1 0 0 0 Стрелка Пирса (или-не) ↓ ¬(A+B) F 10(A, B) 1 0 0 1 Эквиваленция (равнозначность) АΞВ A&B+¬A&¬B F 11(A, B) 1 0 Инвертор В ¬B F 12(A, B) 1 0 1 1 Импликация B->A Название ¬A&B

Элементарная конъюнкция Конъюнкция переменных функции или их отрицаний.

Дизъюнктивная нормальная форма (ДНФ) Дизъюнкция элементарных конъюнкций

Аналитическое представление табличнозаданной функции А В F(A, B) 0 0 1 0 1 1 1 0
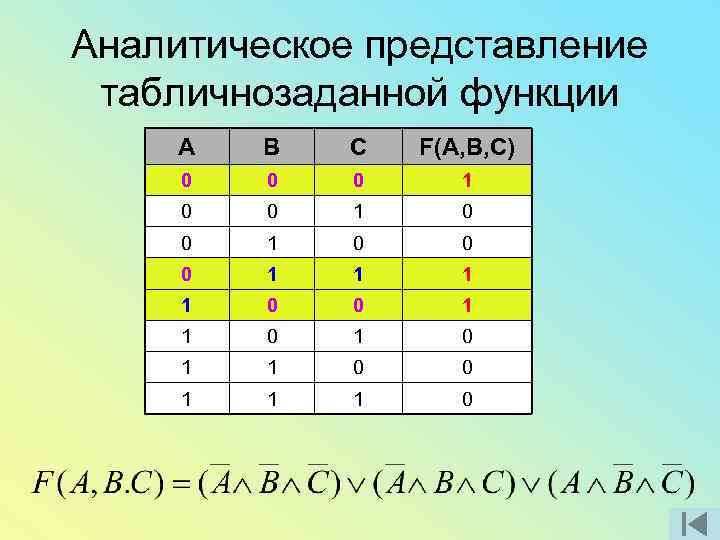
Аналитическое представление табличнозаданной функции A B C F(A, B, C) 0 0 0 1 0 0 0 1 1 0 1 1 0 0 1 1 1 0

Элементарная дизъюнкция Дизъюнкция переменных функции или их отрицаний.

Конъюнктивная нормальная форма (КНФ) Конъюнкция элементарных дизъюнкций

Аналитическое представление табличнозаданной функции А В F(A, B) 0 0 1 0 1 1 1 0
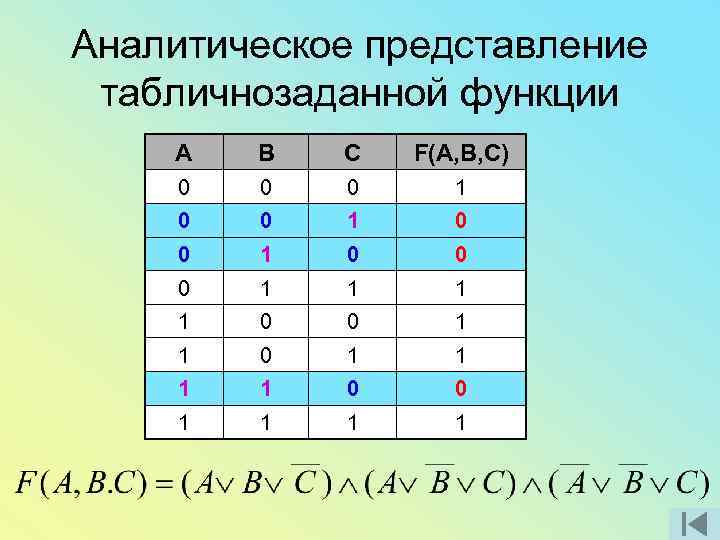
Аналитическое представление табличнозаданной функции A B C F(A, B, C) 0 0 0 1 0 0 0 1 1 1 1

Решение логических задач Задача 1. Определить, кто из подозреваемых участвовал в преступлении, если известно: 1). Если Иванов не участвовал или Петров участвовал, то Сидоров участвовал. 2). Если Иванов не участвовал, то Сидоров не участвовал.

Решение логических задач Обозначим высказывания буквами: И: Иванов участвовал в преступлении. П: Петров участвовал в преступлении. С: Сидоров участвовал в преступлении.

Решение логических задач • Если Иванов не участвовал или Петров участвовал, то Сидоров участвовал. • Если Иванов не участвовал, то Сидоров не участвовал. - истинное высказывание

Решение логических задач Тогда - истинное высказывание
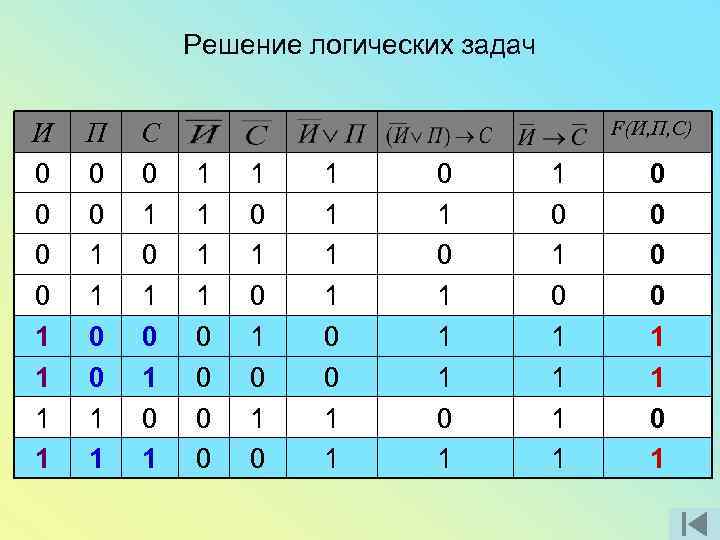
Решение логических задач И 0 0 1 1 П 0 0 1 1 С 0 1 0 1 F(И, П, С) 1 1 0 0 1 0 1 0 1 1 0 1 0 1 1 1 1 0 0 1 1 0 1

Решение логических задач Вывод: Иванов участвовал в преступлении. Об участии в преступлении Петрова и Сидорова на основании этих данных ничего сказать нельзя.

Сложные функции A B 1 1 1 0 0 C

Сложные функции A B 1 0 1 1 0 0 0 1 1 0 C

Сложные функции A B C 1 0 1 0 0 1 1 1 0 1

Сложные функции A B C 1 0 1 1 0 0 1 1 1 1 0 1 1
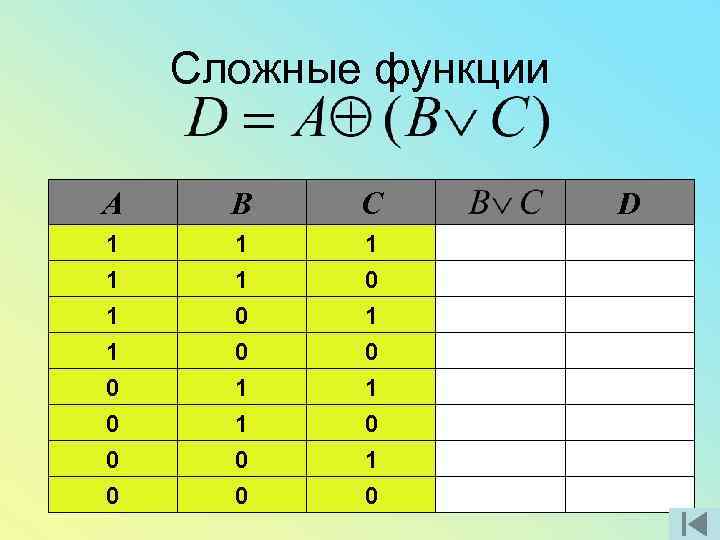
Сложные функции A B C 1 1 1 0 0 1 1 0 0 0 1 0 1 0 D
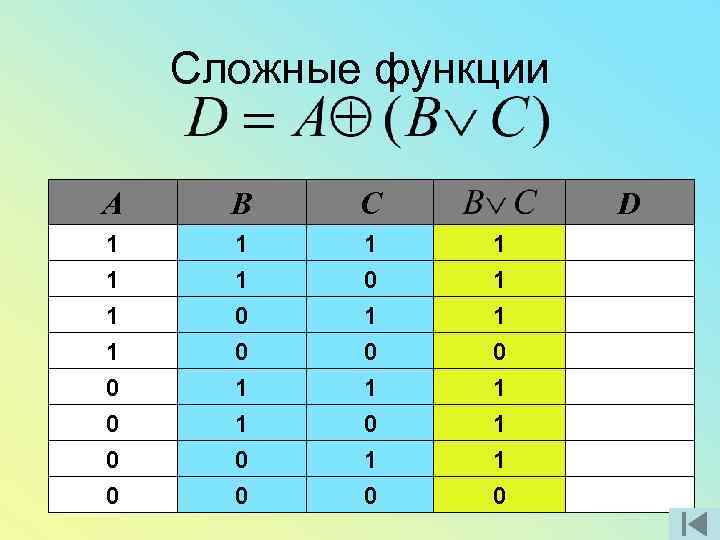
Сложные функции A B C D 1 1 1 1 0 0 1 1 0 0 0 1 0 1 1 1 0
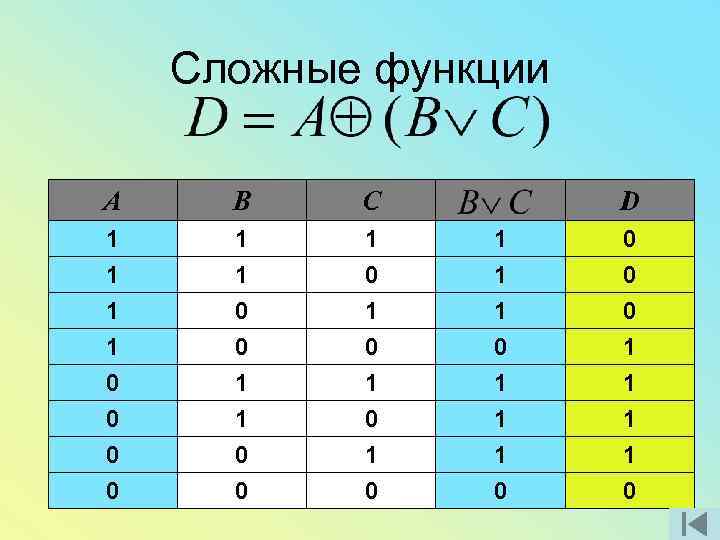
Сложные функции A B C D 1 1 0 1 1 1 0 0 1 1 0 0 0 1 0 1 1 1 0 0 0 1 1 0
МПГУ Операции математической логики1.ppt