Правило суммы Если объект А можно


Правило суммы Если объект А можно выбрать n способами, а объект В можно выбрать m способами, то объект (А или В) можно выбрать m+n способами.

Примеры применения правила суммы В магазине есть пять видов коробок конфет и четыре вида коробок печенья. Таня хочет купить в подарок одну коробку. Сколько вариантов выбора подарка у нее есть? Ответ: 9 вариантов выбора коробки.
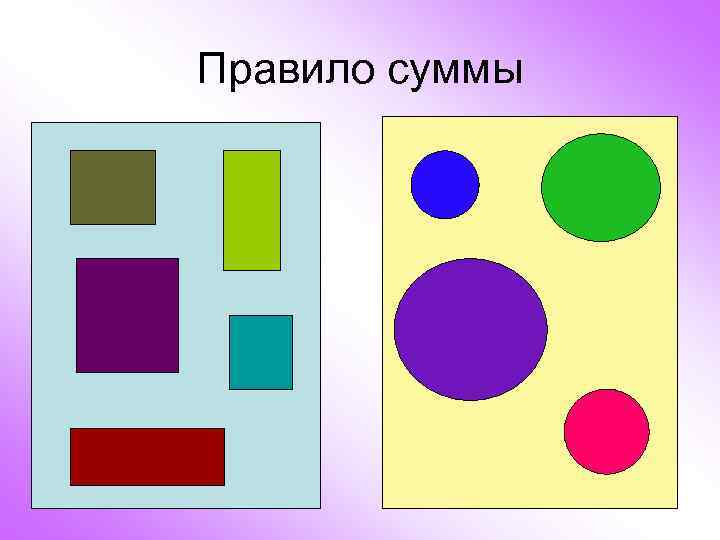
Правило суммы

Правило произведения Если объект А можно выбрать n способами, а после выбора объекта А объект В можно выбрать m способами, то объект (А и В) можно выбрать n*m способами.

Примеры применения правила произведения В магазине есть пять видов коробок конфет и четыре вида коробок печенья. Таня хочет купить в подарок одну коробку конфет и одну коробку печенья. Сколько вариантов выбора подарка у нее есть? Ответ: 20 вариантов выбора подарка.
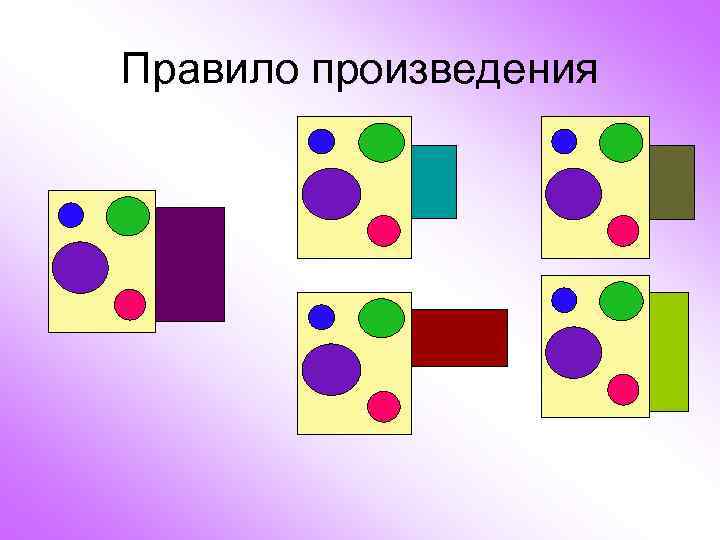
Правило произведения

Упорядоченные множества Множество называется упорядоченным, если каждому элементу этого множества поставлено в соответствие некоторое число (номер элемента) от 1 до n , где n - число элементов множества (мощность множества).

Перестановки Есть неупорядоченное множество А мощности n. А={a 1, a 2, …an } Упорядоченное некоторым способом подмножество мощности n множества А называется перестановкой элементов множества А Количество перестановок Рn =n!

Факториал n! = 1*2*3*…*n 2! = 1*2 = 2 3! = 1*2*3 = 6 4! = 1*2*3*4 = 24 5! = 1*2*3*4*5 = 120

Перестановки Пусть множество А мощности 3 А={1, 2, 3 } Упорядоченные подмножества А={ 1, 2, 3 } А={2, 1, 3 } А={3, 1, 2 } А={ 1, 3, 2 } А={2, 3, 1 } А={3, 2, 1 } Р 3 =3 ! = 6
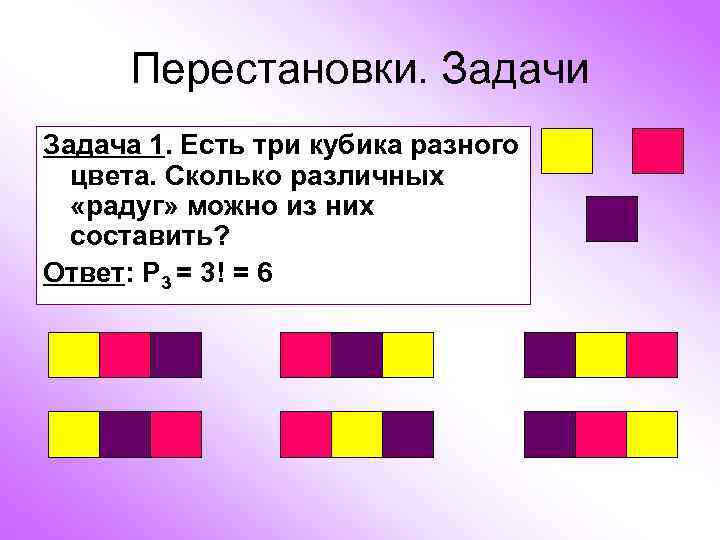
Перестановки. Задачи Задача 1. Есть три кубика разного цвета. Сколько различных «радуг» можно из них составить? Ответ: P 3 = 3! = 6

Перестановки. Задачи Задача 6. Сколько вариантов 6 -значного кода можно составить из цифр 4, 5, 6, 7, 8, 9? Ответ: Р 6= 6! = 720

Размещения Есть неупорядоченное множество А мощности n. А={a 1, a 2, …an } Упорядоченное некоторым способом подмножество множества А мощности m (m

Размещения Количество размещений =n*(n-1)*…*(n-m+1)
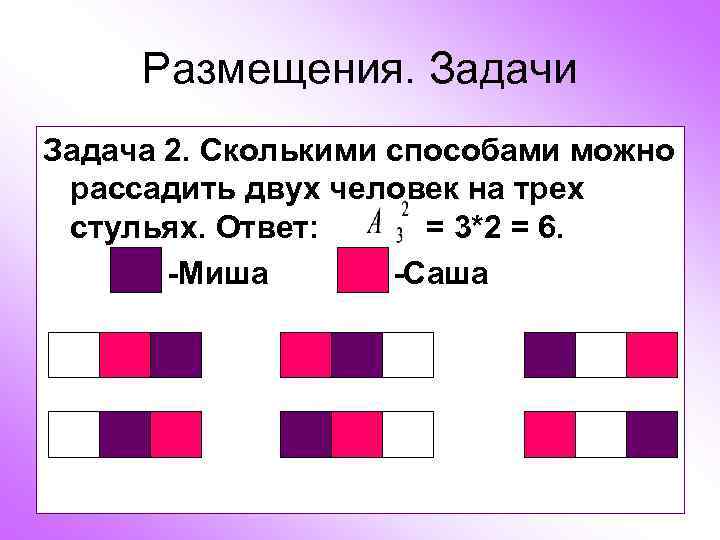
Размещения. Задачи Задача 2. Сколькими способами можно рассадить двух человек на трех стульях. Ответ: = 3*2 = 6. -Миша -Саша

Размещения. Задачи Задача 4. Сколькими способами можно составить программу концерта из 7 номеров, если предлагается выбрать из 10 артистов? Ответ: 151200

Сочетания Есть множество А мощности n. А={a 1, a 2, …an } Неупорядоченное подмножество множества А мощности m (m

Сочетания. Задачи Задача 1. В ящике 2 шара белого цвета, 2 шара синего цвета и 1 шар желтого цвета. Сколькими способами можно выбрать 3 шара (порядок выбора шара не важен) ? Ответ: 10

Сочетания. Задачи Задача 3. Сколькими способами можно выбрать 3 делегатов на профсоюзную конференцию в отделе из 7 человек? Ответ: 35

