Правильные системы точек Пространственная группа задается не только

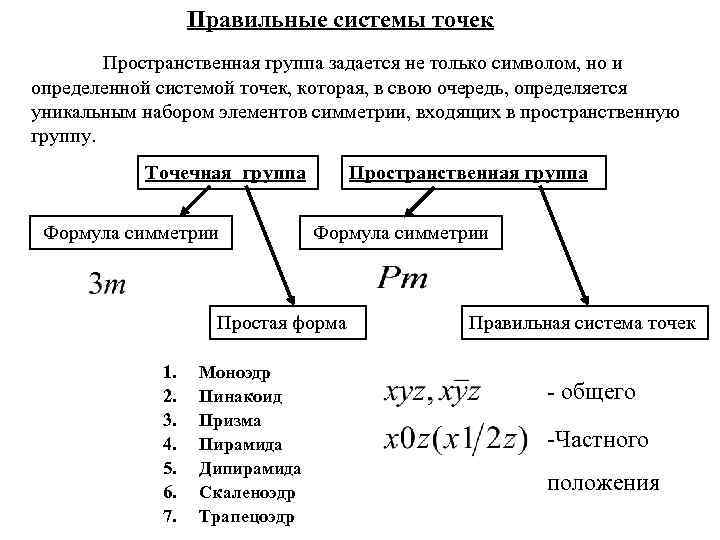Правильные системы точек Пространственная группа задается не только символом, но и определенной системой точек, которая, в свою очередь, определяется уникальным набором элементов симметрии, входящих в пространственную группу. Точечная группа Формула симметрии Пространственная группа Формула симметрии Простая форма 1. 2. 3. 4. 5. 6. 7. Моноэдр Пинакоид Призма Пирамида Дипирамида Скаленоэдр Трапецоэдр Правильная система точек - общего -Частного положения

Правильной системой точек называется полная совокупность точек, которая получается из одной в результате воздействия на нее всех элементов симметрии, входящих в пространственную группу. Если порождающая точка лежит на элементе симметрии, то он на нее не действует. Поэтому в зависимости от положения, в каждую систему может входить неодинаковое число точек. Кратностью системы точек называется число точек входящих в систему. Одной пространственной группе соответствует несколько систем точек разной кратности. Кратность зависит от числа степеней свободы, которое изменяется от 3 до 0: • 3 степени свободы – точка вне элементов симметрии; • 2 степени свободы – точка на плоскости симметрии; • 1 степени свободы – точка на оси симметрии; • 0 степени свободы – точка совпадает с точкой пересечения элементов симметрии точечной группы.

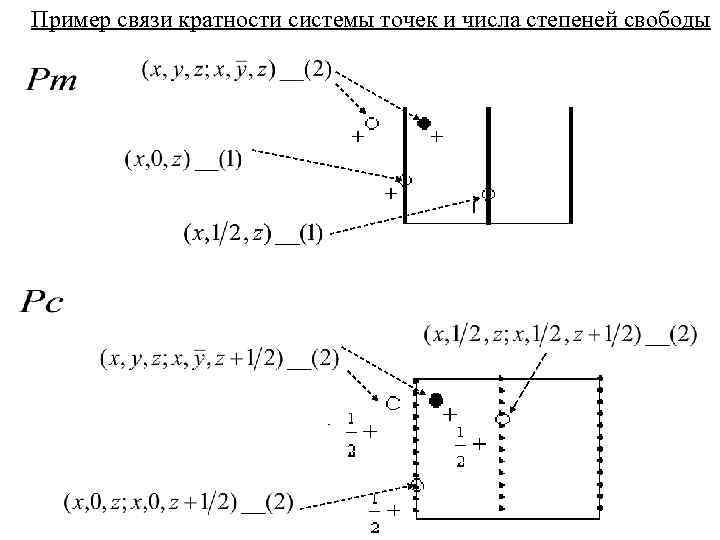Пример связи кратности системы точек и числа степеней свободы

Развитие плана пространственной группы по ее символу (необходимо для определения возможных правильных систем точек данной пространственной группы симметрии) Рассмотрим пример пространственной группы P 4 mm. Сначала строят проекцию системы трансляций, которая задается символом ячейки Бравэ, стоящем на перовом месте и стандартной установкой в тетрагональной сингонии(определяется формулой симметрии). tb OY OX

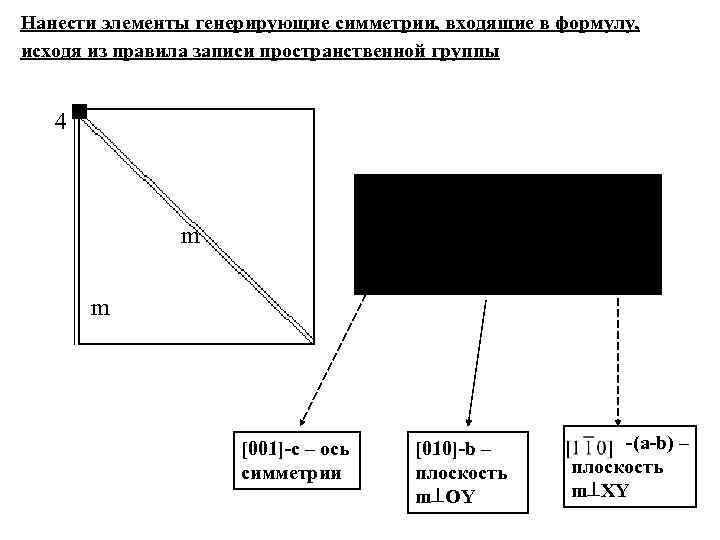Нанести элементы генерирующие симметрии, входящие в формулу, исходя из правила записи пространственной группы 4 m m [001]-c – ось симметрии [010]-b – плоскость m OY -(a-b) – плоскость m XY

Используя теоремы взаимодействия элементов симметрии и действие одних элементов на другие, построить элементы симметрии, которые не входят в формулу Сначала применяют теоремы сложения элементов симметрии континуума, а затем –дисконтинуума. Условия для применения теоремы 1 существуют, но они уже реализованы. На линии пересечения двух плоскостей, входящих в формулу, уже лежит ось симметрии четвертого порядка. Теоремы 2 , 3 и 5 неприменимы, т. к. для них нет условий. По теореме 4 через ось симметрии четвертого порядка должно проходить четыре плоскости зеркального отражения. Таким образом, появляется еще две плоскости зеркального отражения.

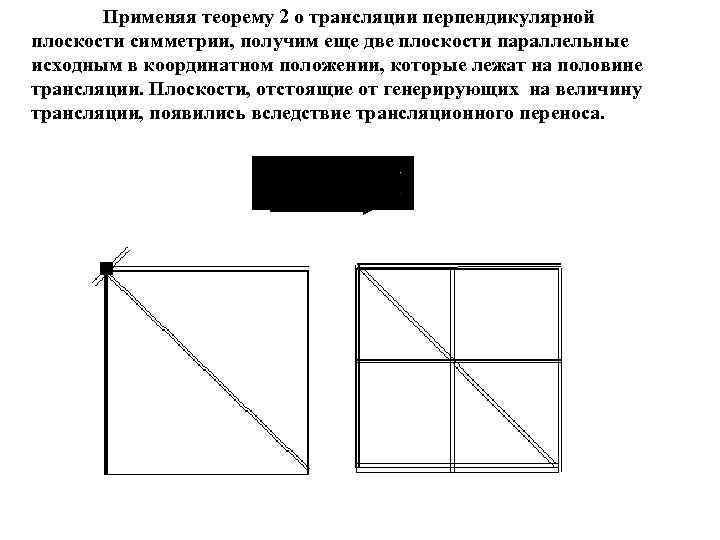Применяя теорему 2 о трансляции перпендикулярной плоскости симметрии, получим еще две плоскости параллельные исходным в координатном положении, которые лежат на половине трансляции. Плоскости, отстоящие от генерирующих на величину трансляции, появились вследствие трансляционного переноса.

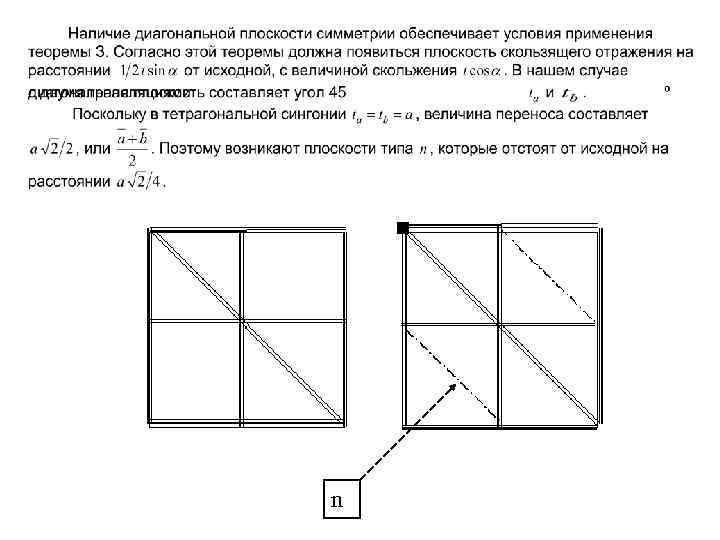n

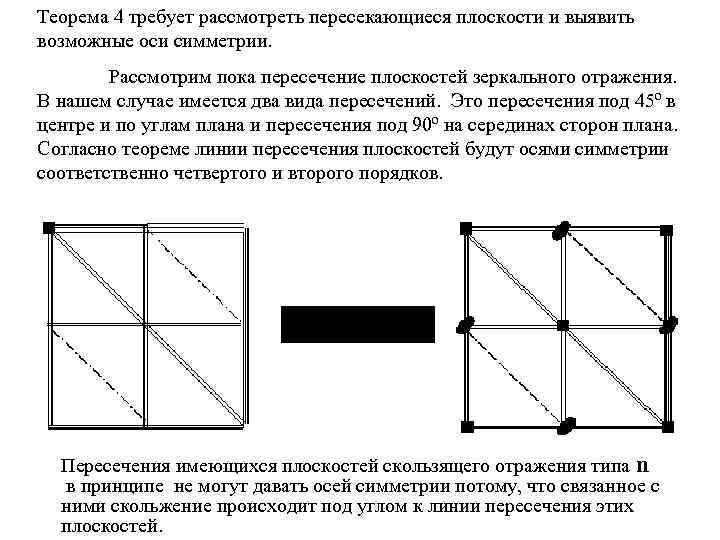Теорема 4 требует рассмотреть пересекающиеся плоскости и выявить возможные оси симметрии. Рассмотрим пока пересечение плоскостей зеркального отражения. В нашем случае имеется два вида пересечений. Это пересечения под 45º в центре и по углам плана и пересечения под 90º на серединах сторон плана. Согласно теореме линии пересечения плоскостей будут осями симметрии соответственно четвертого и второго порядков. Пересечения имеющихся плоскостей скользящего отражения типа n в принципе не могут давать осей симметрии потому, что связанное с ними скольжение происходит под углом к линии пересечения этих плоскостей.

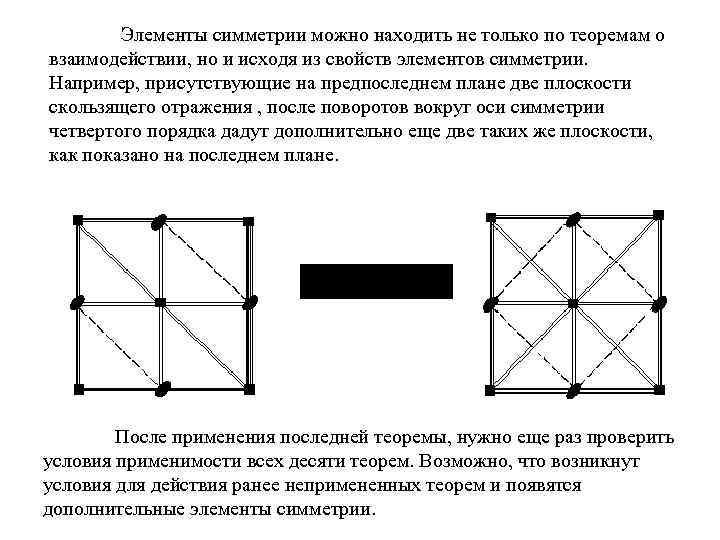Элементы симметрии можно находить не только по теоремам о взаимодействии, но и исходя из свойств элементов симметрии. Например, присутствующие на предпоследнем плане две плоскости скользящего отражения , после поворотов вокруг оси симметрии четвертого порядка дадут дополнительно еще две таких же плоскости, как показано на последнем плане. После применения последней теоремы, нужно еще раз проверить условия применимости всех десяти теорем. Возможно, что возникнут условия для действия ранее непримененных теорем и появятся дополнительные элементы симметрии.

Проверка применения всех теорем Теоремы континуума: 1. 2. 3. 4. 5. Теорема о пересечении двух плоскостей – использована; Теорема о пересечении двух осей – использована; Теорема о пересечении оси симметрии и плоскости зеркального отражения – нет условий; Следствие теоремы о пересечении двух плоскостей (число осей симметрии второго порядка, перпендикулярных оси симметрии высшего порядка, равно порядку этой оси)–нет условий; Следствие теоремы о пересечении двух осей (число плоскостей симметрии, пересекающихся по оси симметрии, равно порядку этой оси)– использована. Теоремы континуума: 1. 2. 3. 4. 5. Последовательное отражение в двух параллельных плоскостях – использована; Сумма плоскости симметрии и перпендикулярной к ней трансляции – использована; Сумма плоскости зеркального отражения и наклонной к ней трансляции– использована; Отражение в двух пересекающихся плоскостях симметрии– использована Сумма оси симметрии и перпендикулярной к ней трансляции – использована.

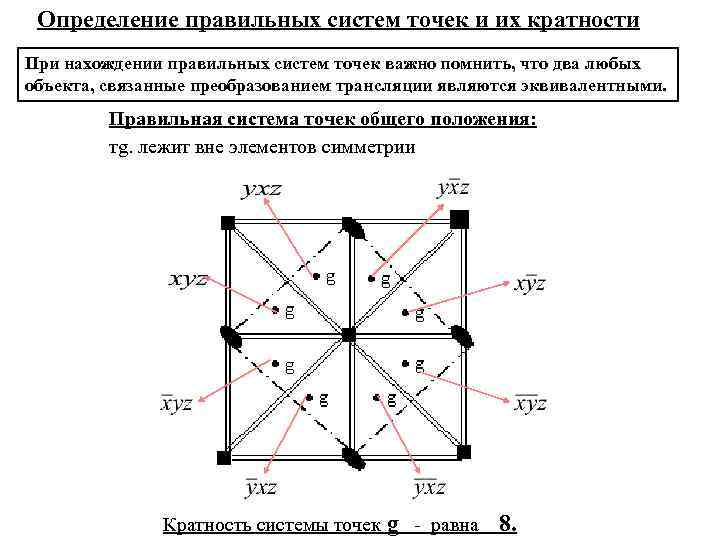Определение правильных систем точек и их кратности При нахождении правильных систем точек важно помнить, что два любых объекта, связанные преобразованием трансляции являются эквивалентными. Правильная система точек общего положения: тg. лежит вне элементов симметрии Кратность системы точек g - равна 8.

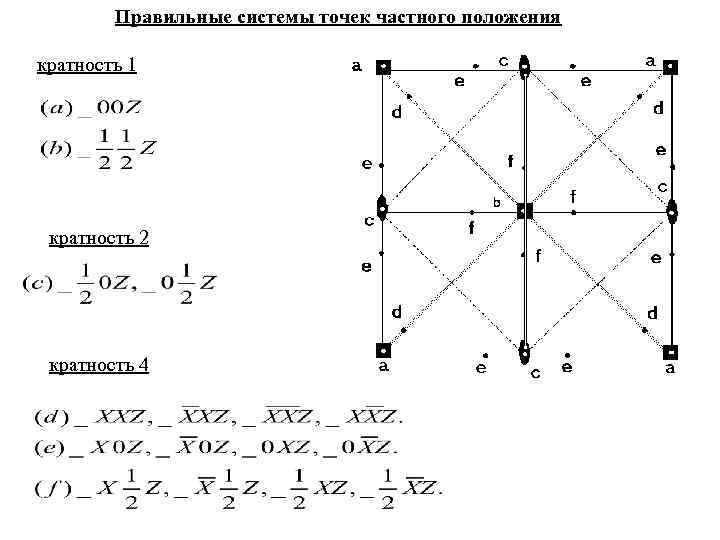Правильные системы точек частного положения кратность 1 кратность 2 кратность 4