Скачать презентацию Правила дифференцирования Найти производную 1 у Скачать презентацию Правила дифференцирования Найти производную 1 у

Производная геометрич смысл.pptx

  • Количество слайдов: 61

Правила дифференцирования Правила дифференцирования

. Найти производную. 1) у= -7 х 3) y=tgx-ctgx 5) у=πх-2 соs 3 x . Найти производную. 1) у= -7 х 3) y=tgx-ctgx 5) у=πх-2 соs 3 x 7) у=(6 - 3 х )²

Применение производной в изучении естественно-научных дисциплин Исаак Ньютон (4 января 1643 – 20 марта Применение производной в изучении естественно-научных дисциплин Исаак Ньютон (4 января 1643 – 20 марта 1727) Ньютон открыл ещё в 1665— 1666 годы, однако не публиковал его до 1704 года. В своих работах функцию называл флюентой, а производную функции – флюксией.

Исаак Ньютон (1643 – 1727) «Когда величина является максимальной или минимальной, в этот момент Исаак Ньютон (1643 – 1727) «Когда величина является максимальной или минимальной, в этот момент она не течет ни вперед, ни назад. »

Задача № 2. Лыжник, спускаясь с горы, движется по закону s(t) = 0, Задача № 2. Лыжник, спускаясь с горы, движется по закону s(t) = 0, 5 t² - t. Найти скорость и ускорение лыжника в момент времени t= 3 с, если расстояние измеряется в метрах. Какое это движение?

Материальная точка движется прямолинейно по закону где x –расстояние от точки отсчёта в Материальная точка движется прямолинейно по закону где x –расстояние от точки отсчёта в метрах, t - время в секундах, измеренное с начала движения. В какой момент времени (в секундах) её скорость была равна 3 м/с?

Применение производной в изучении естественно-научных дисциплин Производная в химии Количество вещества, вступившего в химическую Применение производной в изучении естественно-научных дисциплин Производная в химии Количество вещества, вступившего в химическую реакцию, задается зависимостью: Найти скорость химической реакции через 3 секунды.

1646 г – 1716 г Геометрическая интерпретация производной, впервые данная в конце XVII 1646 г – 1716 г Геометрическая интерпретация производной, впервые данная в конце XVII в. Лейбницем, который основываясь на результатах Ферма и некоторых других выводах, значительно полнее своих предшественников решил задачу о построении касательной к кривой в некоторой точке.

«Если продолжить одно из маленьких звеньев ломаной, составляющей кривую линию, то эта продолженная «Если продолжить одно из маленьких звеньев ломаной, составляющей кривую линию, то эта продолженная таким образом сторона будет называться касательной к кривой. »

Касательная к кривой. 0 1 2 3 4 5 6 7 8 9 10 Касательная к кривой. 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 IIIII I II IIII II IIIII I IIIII I I II II I II IIIII II IIII I II IIIII I IIIII II IIII I II II III

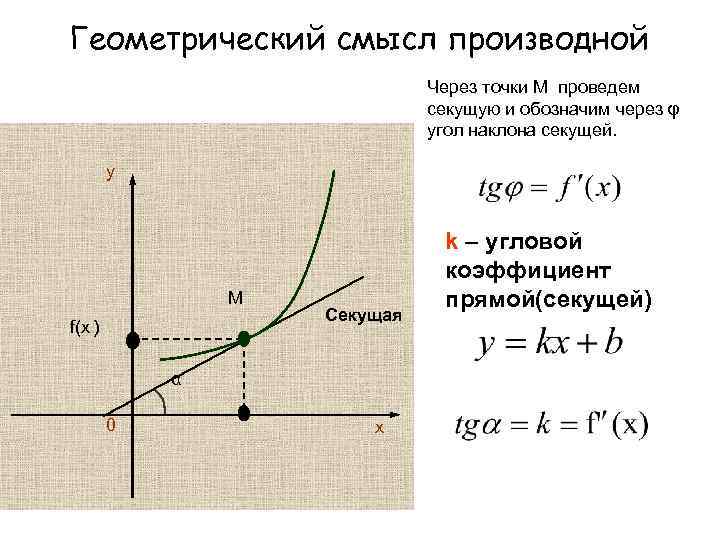Геометрический смысл производной Через точки М проведем секущую и обозначим через φ угол наклона Геометрический смысл производной Через точки М проведем секущую и обозначим через φ угол наклона секущей. y y f(x+ Δx ) М 1 М f(x ) φ 0 х М f(x ) x+Δx х Секущая α 0 х k – угловой коэффициент прямой(секущей)

а b а b

y= kx y y a o x x y противолежащий катет k = = y= kx y y a o x x y противолежащий катет k = = tg a прилежащий катет x

y ща я k – угловой коэффициент прямой(секущей) Се ку я льна те Каса y ща я k – угловой коэффициент прямой(секущей) Се ку я льна те Каса 0 х Секущая стремится занять положение касательной. То есть, касательная есть предельное положение секущей.

y k – угловой коэффициент прямой(касательной) я льна ате Кас 0 х Геометрический смысл y k – угловой коэффициент прямой(касательной) я льна ате Кас 0 х Геометрический смысл производной Производная от функции в данной точке равна угловому коэффициенту касательной, проведенной к графику функции в этой точке.

Производная от функции в данной точке равна угловому коэффициенту касательной, проведенной к графику функции Производная от функции в данной точке равна угловому коэффициенту касательной, проведенной к графику функции в этой точке.

В чем состоит геометрический смысл производной? Значение производной в точке Тангенс угла наклона касательной В чем состоит геометрический смысл производной? Значение производной в точке Тангенс угла наклона касательной к положительно му направлению оси ОХ Угловой коэффициент касательной

Найдите угловой коэффициент касательной проходящей через точку А графика функции f. f (x) = Найдите угловой коэффициент касательной проходящей через точку А графика функции f. f (x) = х2 - х, А(1; 3) f ′(x) = 2 х - 1 f ′(x 0) = f ′(1) = 2· 1 - 1 = 1 к = 1 , tg α = 1, α = 45º. Ответ: угловой коэффициент касательной равен 1, угол наклона касательной 45º.

Найдите угловой коэффициент касательной проходящей через точку А графика функции f. f (x) = Найдите угловой коэффициент касательной проходящей через точку А графика функции f. f (x) = х3 + 2 х – 6, х0 = - 1. f ′(x) = 3 х2 + 2 – 0 = 3 х2 + 2 f ′(x 0) = f ′(-1) = 3·(- 1)2 + 2 = 3· 1+2 = 5 к = 5 Ответ: угловой коэффициент касательной равен 5.

Найдите угловой коэффициент касательной. 3 + 4 х, х 1. f (x) = х Найдите угловой коэффициент касательной. 3 + 4 х, х 1. f (x) = х 0 = 2 2 - 3 х + 5, х 2. f (x) = х 0 = -3

Решение задач 1. Найдите тангенс угла наклона касательной, проведенной к графику функции f(x) = Решение задач 1. Найдите тангенс угла наклона касательной, проведенной к графику функции f(x) = – 0, 5 х2 в его точке с абсциссой х0 = – 3. 2. Найдите угловой коэффициент касательной, проведенной к графику функции f(x) = х5 – 5 х2– 3 в его точке с абсциссой х0 = – 1.

К графику функции проведена касательная с угловым коэффициентом, равным к. Найдите координаты точки касания. К графику функции проведена касательная с угловым коэффициентом, равным к. Найдите координаты точки касания. f (x) = 1 – 5 х – х2, к = 9. к = f ′( х0), f ′( х0) = 9 f ′(x) = 0 -5 -2 х = -5 -2 х -5 - 2 x = 9 - 2 x= 9 +5 - 2 x= 14 x = -7 Точка касания принадлежит графику функции. у = f ( х0) = f (-7) = 1 - 5·(-7) – (-7)2 = 1 + 35 – 49 = 36 - 49 = -13 Ответ: координаты точки касания (-7; -13).

К графику функции проведена касательная с угловым коэффициентом, равным к. Найдите координаты точки касания. К графику функции проведена касательная с угловым коэффициентом, равным к. Найдите координаты точки касания. 1. f (x) = 5 – х2, к = 7. 2. f (x) = 4 +3 х + 2 х2, к = 3.

Прямая у = 4 х + 11 параллельна касательной к графику функции у = Прямая у = 4 х + 11 параллельна касательной к графику функции у = х2 + 8 х + 6. Найдите абсциссу точки касания. Решение: у = х2 + 8 х + 6. у = 4 х + 11 f ′(x) = (х2 + 8 х + 6)′ = 2 x + 8. k=4 k = f ′(xo) = 4 2 х + 8 = 4, 2 x =4 -8, 2 x=-4 х= – 2. Ответ: – 2.

1. Прямая y = 7 x – 5 параллельна касательной к графику функции f(x) 1. Прямая y = 7 x – 5 параллельна касательной к графику функции f(x) = x 2 + 6 x – 8. Найдите абсциссу точки касания 2. Найдите точку касания прямой y=3 x+8 и графика функции y=x 3+x 2− 5 x− 4. В ответе укажите абсциссу этой точки. 3. Прямая у = – 5 х + 4 параллельна касательной к графику функции у = х2+3 х+6. Найдите абсциссу точки касания.

k =tga = f'(x ) > 0 k =tga = f'(x ) < 0 k =tga = f'(x ) > 0 k =tga = f'(x ) < 0 k =tga = f'(x ) = 0 Если угол наклона прямой, то тангенс не существует, а значит, производная не существует.

Закрепление и расширение знаний по данной теме при решении прототипов В 8 из открытого Закрепление и расширение знаний по данной теме при решении прототипов В 8 из открытого банка заданий ЕГЭ. Тип задачи На рисунке изображен график функции. Прямая, проходящая через начало координат, касается графика этой функции в точке с абсциссой 8. Найдите Главный Способ (алгоритм) решения вопрос задачи 1. Провожу диагональ прямоугольника из начала отсчета 2. Рассматриваю прямоугольный треугольник 3. По геометрическому смыслу производной… 4. Из треугольника нахожу значение тангенса угла наклона касательной к оси Ох

Решении прототипов В 8 из открытого банка заданий ЕГЭ Тип задачи На рисунке изображён Решении прототипов В 8 из открытого банка заданий ЕГЭ Тип задачи На рисунке изображён график функции и касательная к нему в точке с абсциссой. Найдите значение производной функции в точке. Главный вопрос задачи Способ (алгоритм) решения 1. Достраиваю до прямоугольного треугольника с острым углом, равным углу наклона касательной к оси Ох 2. По геометрическому смыслу производной… 3. Нахожу тангенс угла наклона касательной к оси Ох.

f’(x 0) = tg у y= f(x) 0 x 0 х f’(x 0) = tg у y= f(x) 0 x 0 х

k =tga = f'(x ) > 0 k =tga = f'(x ) < 0 k =tga = f'(x ) > 0 k =tga = f'(x ) < 0 k =tga = f'(x ) = 0 Если угол наклона прямой, то тангенс не существует, а значит, производная не существует.

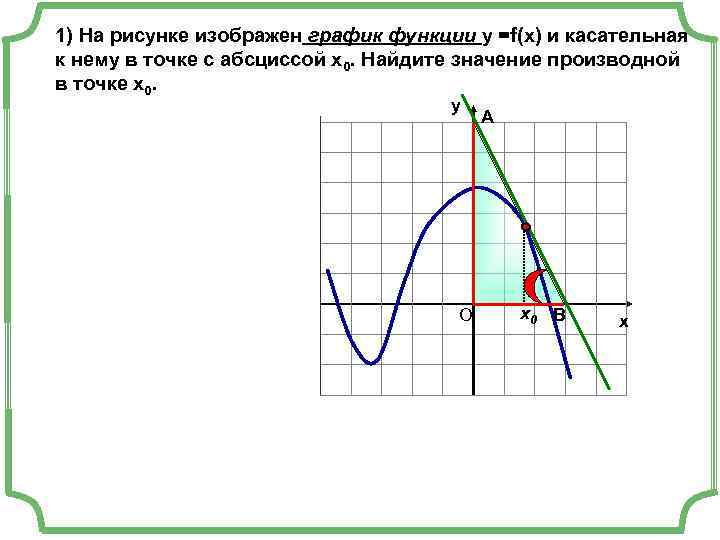1) На рисунке изображен график функции у =f(x) и касательная к нему в точке 1) На рисунке изображен график функции у =f(x) и касательная к нему в точке с абсциссой х0. Найдите значение производной в точке х0. y А х0 В x О

На рисунке изображен график функции y = f (x), и касательная к нему в На рисунке изображен график функции y = f (x), и касательная к нему в точке с абсциссой х0. Найдите значение производной функции y = f (x) в точке х0. a) б) А С В А С Решение. Ответ: - 0, 5. Ответ: 0, 75. В

Самостоятельная работа Самостоятельная работа

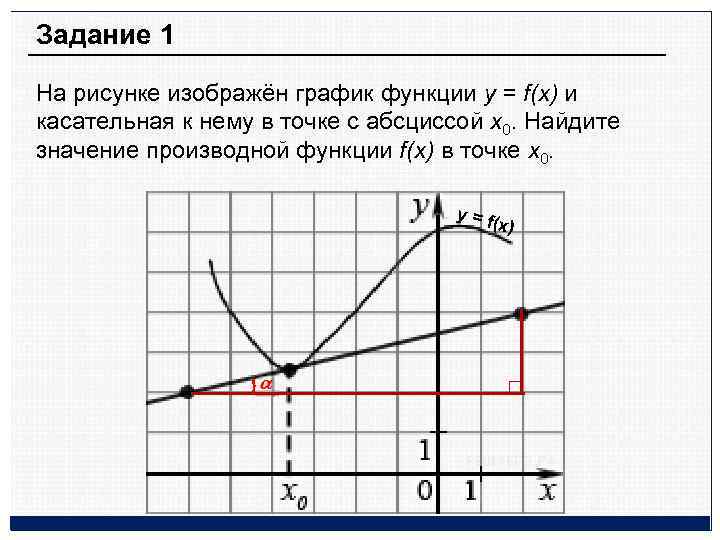Задание 1 На рисунке изображён график функции y = f(x) и касательная к нему Задание 1 На рисунке изображён график функции y = f(x) и касательная к нему в точке с абсциссой x 0. Найдите значение производной функции f(x) в точке x 0. у = f (x)

Задание 1 На рисунке изображён график функции y = f(x) и касательная к нему Задание 1 На рисунке изображён график функции y = f(x) и касательная к нему в точке с абсциссой x 0. Найдите значение производной функции f(x) в точке x 0. у = f (x)

Задание 1 На рисунке изображён график функции y = f(x) и касательная к нему Задание 1 На рисунке изображён график функции y = f(x) и касательная к нему в точке с абсциссой x 0. Найдите значение производной функции f(x) в точке x 0. у = f (x)

Задание 1 На рисунке изображён график функции y = f(x) и касательная к нему Задание 1 На рисунке изображён график функции y = f(x) и касательная к нему в точке с абсциссой x 0. Найдите значение производной функции f(x) в точке x 0. у = f (x) 2 8

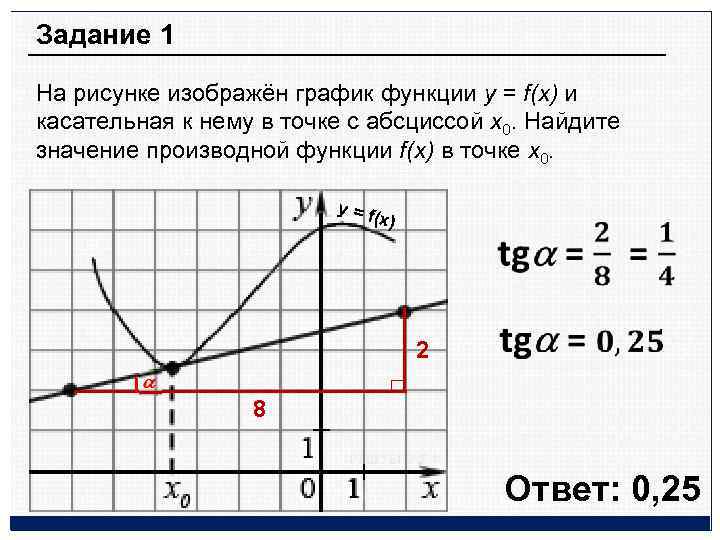Задание 1 На рисунке изображён график функции y = f(x) и касательная к нему Задание 1 На рисунке изображён график функции y = f(x) и касательная к нему в точке с абсциссой x 0. Найдите значение производной функции f(x) в точке x 0. у = f (x) 2 8 Ответ: 0, 25

На рисунке изображен график у = f(x) – производной функции f(x), определенной на интервале На рисунке изображен график у = f(x) – производной функции f(x), определенной на интервале (– 7; 5) и касательная к нему в точке с абсциссой хо. Найдите значение производной функции f(x) в точке хо. у = f(x) В α хо 5 α А 4 С Ответ: 1, 25. № 1 Решение: Значение производной функции f ′(хo) = tg α = k равно угловому коэффициенту касательной, проведенной к графику этой функции в данной точке. В нашем случае k > 0, так как α – острый угол (tg α > 0). Чтобы найти угловой коэффициент, выберем две точки А и В, лежащие на касательной, абсциссы и ординаты которых − целые числа. Теперь определим модуль углового коэффициента. Для этого построим треугольник ABC. tg α = ВС : АС = 5 : 4 = 1, 25

На рисунке изображен график функции у = f(x), определенной на интервале (– 10; 2) На рисунке изображен график функции у = f(x), определенной на интервале (– 10; 2) и касательная к нему в точке с абсциссой хо. Найдите значение производной функции f(x) в точке хо. В у = f(x) α 6 хо С 8 180°− α Ответ: − 0, 75. А № 2 Решение: Значение производной функции f ′(хo) = tg α = k равно угловому коэффициенту касательной, проведенной к графику этой функции в данной точке. В нашем случае k < 0, так как α – тупой угол (tg α < 0). Чтобы найти угловой коэффициент, выберем две точки А и В, лежащие на касательной, абсциссы и ординаты которых − целые числа. Теперь определим модуль углового коэффициента. Для этого построим треугольник ABC. tg(180°− α) = ВС : АС = 6 : 8 = 0, 75 tg α = − tg (180°− α) = − 0, 75

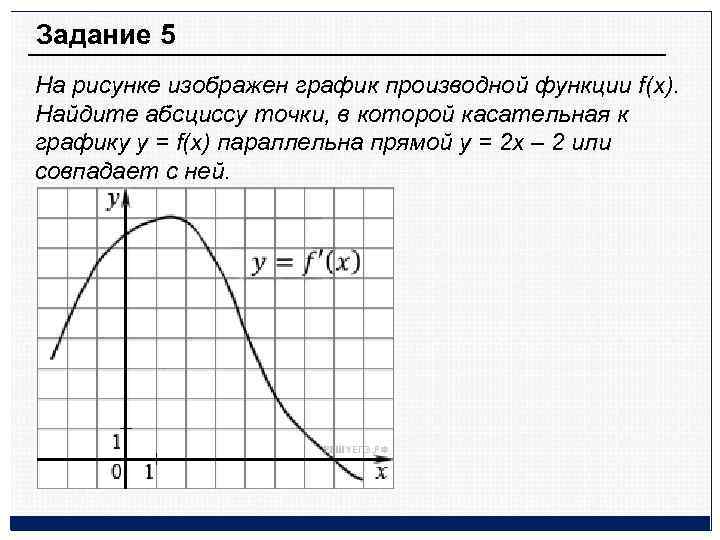Задание 5 На рисунке изображен график производной функции f(x). Найдите абсциссу точки, в которой Задание 5 На рисунке изображен график производной функции f(x). Найдите абсциссу точки, в которой касательная к графику y = f(x) параллельна прямой y = 2 x – 2 или совпадает с ней.

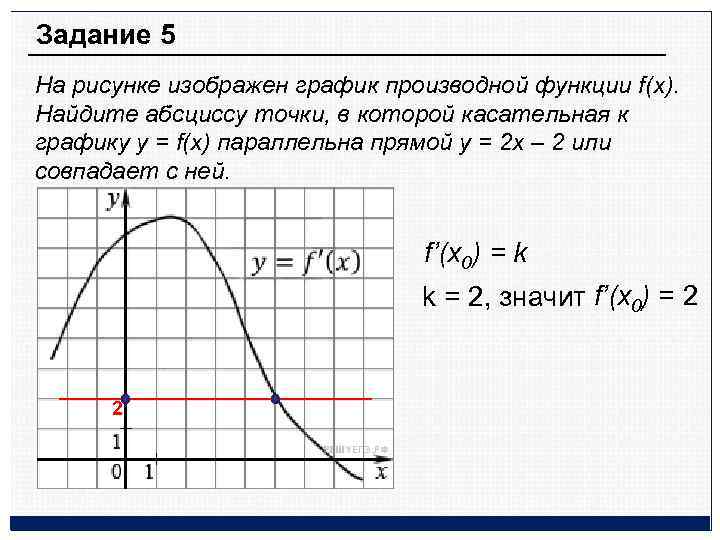Задание 5 На рисунке изображен график производной функции f(x). Найдите абсциссу точки, в которой Задание 5 На рисунке изображен график производной функции f(x). Найдите абсциссу точки, в которой касательная к графику y = f(x) параллельна прямой y = 2 x – 2 или совпадает с ней. f’(x 0) = k k = 2, значит f’(x 0) = 2 2

Задание 5 На рисунке изображен график производной функции f(x). Найдите абсциссу точки, в которой Задание 5 На рисунке изображен график производной функции f(x). Найдите абсциссу точки, в которой касательная к графику y = f(x) параллельна прямой y = 2 x – 2 или совпадает с ней. f’(x 0) = k k = 2, значит f’(x 0) = 2 х = 5 2 5 Ответ: 5

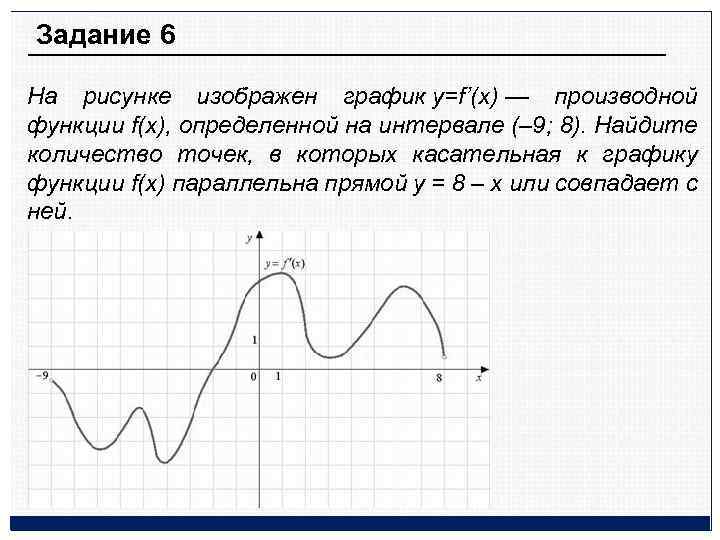Задание 6 На рисунке изображен график y=f’(x) — производной функции f(x), определенной на интервале Задание 6 На рисунке изображен график y=f’(x) — производной функции f(x), определенной на интервале (– 9; 8). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y = 8 – x или совпадает с ней.

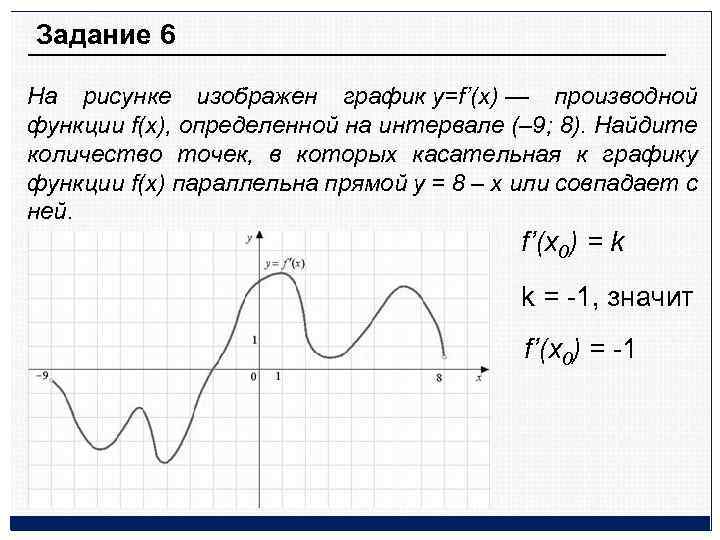Задание 6 На рисунке изображен график y=f’(x) — производной функции f(x), определенной на интервале Задание 6 На рисунке изображен график y=f’(x) — производной функции f(x), определенной на интервале (– 9; 8). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y = 8 – x или совпадает с ней. f’(x 0) = k k = -1, значит f’(x 0) = -1

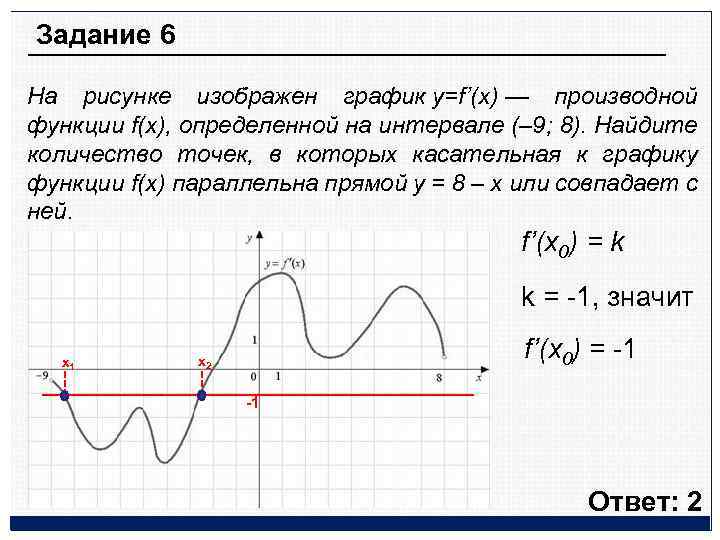Задание 6 На рисунке изображен график y=f’(x) — производной функции f(x), определенной на интервале Задание 6 На рисунке изображен график y=f’(x) — производной функции f(x), определенной на интервале (– 9; 8). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y = 8 – x или совпадает с ней. f’(x 0) = k k = -1, значит х1 f’(x 0) = -1 х2 -1 Ответ: 2

Задачи из ЕГЭ (В 8) На рисунке изображены графики функции y=f(x) и касательной к Задачи из ЕГЭ (В 8) На рисунке изображены графики функции y=f(x) и касательной к нему в точке с абсциссой . Найдите значение производной функции f(x) в точке .

Задачи из ЕГЭ (В 8) На рисунке изображены графики функции y=f(x) и касательной к Задачи из ЕГЭ (В 8) На рисунке изображены графики функции y=f(x) и касательной к нему в точке с абсциссой . Найдите значение производной функции f(x) в точке .

На рисунке изображен график функции y = f (x), касательная к этому графику, проведенная На рисунке изображен график функции y = f (x), касательная к этому графику, проведенная в точке х0, проходит через начало координат. Найдите f'(х0). Решите самостоятельно! 1 х0= 2 3 х0= - 4 Ответ: 2. Ответ: - 0, 5. 2 х0= 4 х0= - 4 Ответ: 0, 5. 4 Ответ: 0, 75.