ПРАКТИКА № 9 2 КУРС 2012 -2013 Math. CAD
Вектора и матрицы Задача 1. Дана матрица Вычислить матрицы Задача 2. Вычислить матрицы О 1 = D-1 , O 3 = D-3 Проверить правильность вычисления этих матриц, т. е. O 1* P 1=E (единичная матрица) O 3*P 3=E
Вектора и матрицы РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ (СЛАУ)
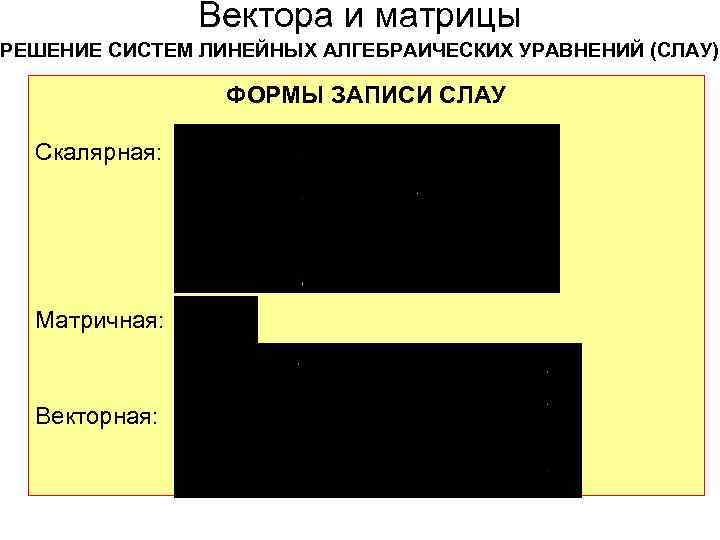Вектора и матрицы РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ (СЛАУ) ФОРМЫ ЗАПИСИ СЛАУ Скалярная: Матричная: Векторная:
Вектора и матрицы РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ (СЛАУ) УСЛОВИЕ СУЩЕСТВОВАНИЯ РЕШЕНИЯ СЛАУ Система Ax=f имеет единственное решение, если det A 0 МЕТОДЫ РЕШЕНИЯ СЛАУ : • Точные • Приближенные (итерационные) ТОЧНЫЕ МЕТОДЫ РЕШЕНИЯ СЛАУ : • Обратной матрицы • Крамера • Гаусса
Вектора и матрицы РЕШЕНИЕ СЛАУ МЕТОДОМ ОБРАТНОЙ МАТРИЦЫ Пусть det A 0 Тогда существует A– 1 - обратная матрица: A A– 1= A– 1 A = E, где E – единичная матрица. Пусть A– 1 известна. Умножая на нее СЛАУ слева, получим: По свойству обратной матрицы: По свойству единичной матрицы: Метод используется для решения небольших систем, т. к. нахождение обратной матрицы – трудоемкий процесс
Вектора и матрицы РЕШЕНИЕ СЛАУ МЕТОДОМ ОБРАТНОЙ МАТРИЦЫ В MATHCAD Пример 1. Дана система линейных алгебраических уравнений Решить СЛАУ методом обратной матрицы 1. Задаем массивы:
Вектора и матрицы РЕШЕНИЕ СЛАУ МЕТОДОМ ОБРАТНОЙ МАТРИЦЫ В MATHCAD 2. Находим определитель det A: 3. Находим обратную матрицу A– 1: 4. Находим решение: 5. Проверка решения:
Вектора и матрицы РЕШЕНИЕ СЛАУ МЕТОДОМ КРАМЕРА Пусть det A 0 Построим m вспомогательных матриц i-й столбец Решения находим по формулам: i=1, 2, …m. Метод используется для решения небольших систем, т. к. нахождение определителей – трудоемкая операция
Вектора и матрицы РЕШЕНИЕ СЛАУ МЕТОДОМ КРАМЕРА В MATHCAD Пример 2. Дана система линейных алгебраических уравнений Решить СЛАУ методом обратной матрицы 1. По умолчанию элементы массива нумеруются с нуля. Для того, чтобы элементы нумеровались с единицы:
Вектора и матрицы РЕШЕНИЕ СЛАУ МЕТОДОМ КРАМЕРА В MATHCAD 2. Задаем массивы: 3. Задаем дискретную переменную i (меняется от 1 до 4 с шагом 1):
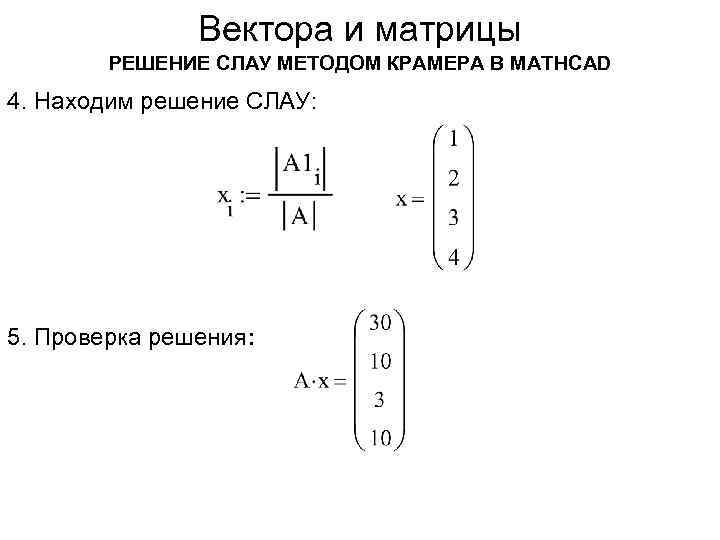Вектора и матрицы РЕШЕНИЕ СЛАУ МЕТОДОМ КРАМЕРА В MATHCAD 4. Находим решение СЛАУ: 5. Проверка решения:
Вектора и матрицы РЕШЕНИЕ СЛАУ Задача 3. Дана система линейных алгебраических уравнений Решить СЛАУ: 1) Методом обратной матрицы 2) Методом Крамера
Вектора и матрицы Размер и диапазон значений массива • rows(A) – число строк в массиве A • cols(A) – число столбцов в массиве A • length(v) – число элементов в векторе v • last(v) – индекс последнего элемента в векторе v • max(A) –cамый большой элемент в массиве A • min(A) –cамый маленький элемент в массиве A • rank(A) – ранг матрицы А, т. е. число линейно независимых строк или столбцов • tr(A) – след матрицы А, т. е. сумму диагональных элементов • mean (A) – среднее значение элементов массива А
Формирование матриц • identity(n) – формирует единичную матрицу n x n • diag(v) – формирует диагональную матрицу, содержащую на диагонали элементы вектора v • matrix(m, n, f) – создает и заполняет матрицу размером m x n, элемент которой, расположенный в строке i и столбце j, равен f(i, j) • augment (A, B) – формирует массив, располагая матрицу B справа от матрицы А (обе матрицы должны иметь одинаковое количество строк) • stack (A, B) - формирует массив, располагая матрицу B снизу от матрицы А (обе матрицы должны иметь одинаковое количество столбцов) • submatrix (A, ir, jn, ic, jc) – формирует подматрицу, содержащую строки с ir по jn и столбцы с ic до jc исходной матрицы А
Вектора и матрицы Задача 4. Откройте новый документ. Даны матрицы Задание 1. Используя функцию identity , сформируйте единичную матрицу порядка 5 Задание 2. Используя функции diag, cформируйте диагональную матрицу с диагональными элементами из вектора B Задание 3. Вычислите число строк и столбцов матрицы A, ее наибольший и наименьший элемент, ее ранг. Задание 4. Вычислите определитель и обратную матрицу для произведения матриц A*AT
Операторы математического анализа Задача 5. Вычислить, используя оператор суммирования: 3) 1) 2) , где Задача 6. Вычислить производную: Задача 7. Найти пределы (панель Calculus, Symbolic):
Решение уравнений (solve) Задача 8. Решить уравнение: Задача 9. Решить систему уравнений: