ПрактикаЖБК-41.ppt
- Количество слайдов: 146

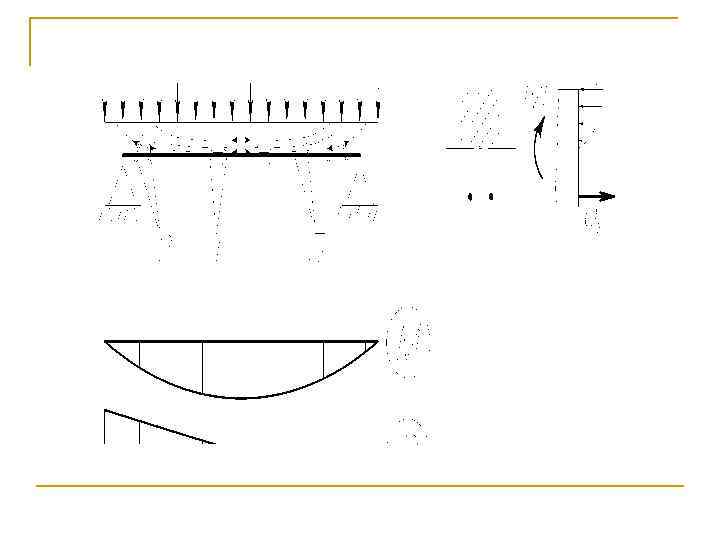
Практическое занятие № 4 Изгибаемый элемент таврового сечения
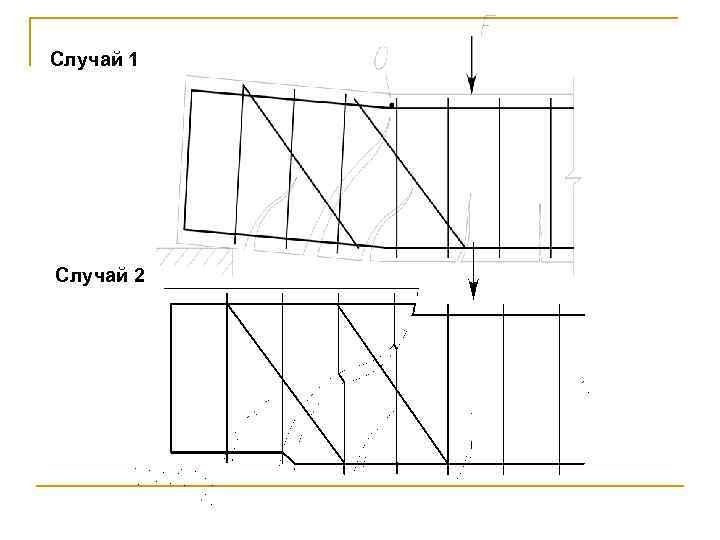
Случай 1 Случай 2

Для обеспечения прочности наклонных сечений изгибаемых элементов расчет должен производиться: ü на сжатие в полосе бетона стенки балки между наклонными трещинами; ü по наклонной трещине на действие поперечной силы; ü по наклонной трещине на действие изгибающего момента.
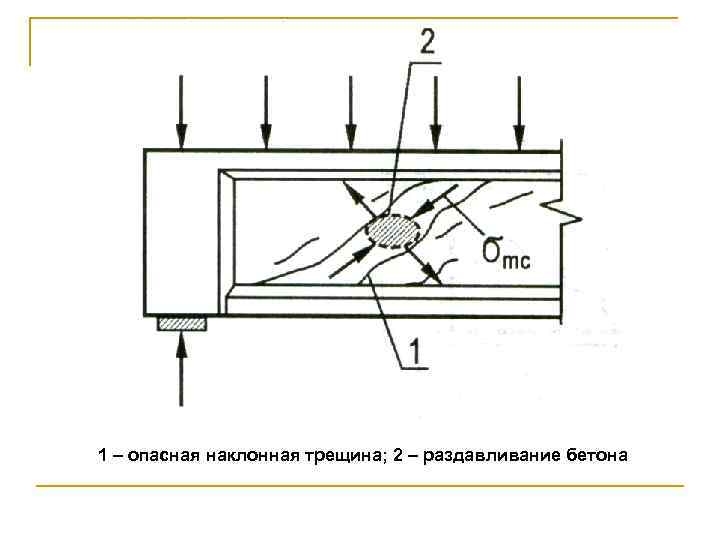
1 – опасная наклонная трещина; 2 – раздавливание бетона

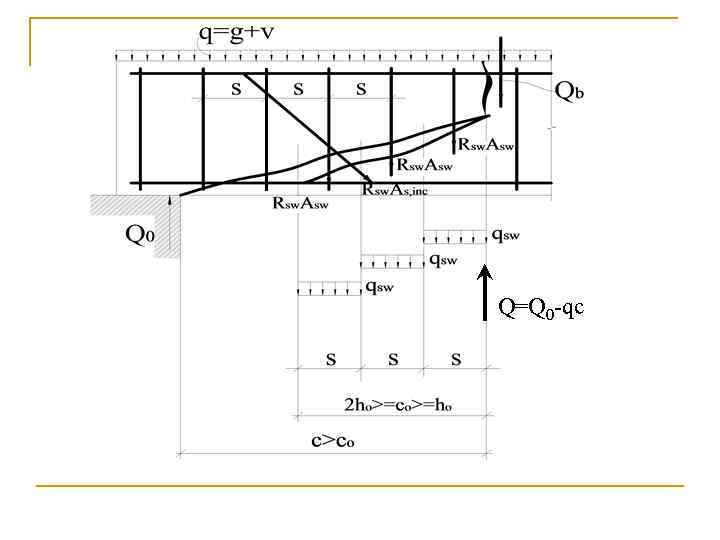
Q=Q 0 -qc

Пример № 7. Подбор поперечной рабочей арматуры изгибаемого элемента
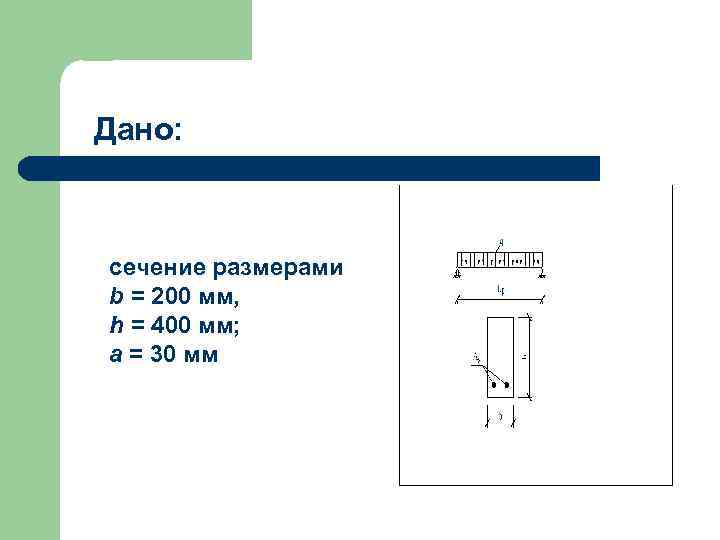
Дано: сечение размерами b = 200 мм, h = 400 мм; а = 30 мм

Дано: • пролет свободно опертой балки Lр = 5, 5 м; • поперечная арматура А 240; • бетон класса В 15; • полная равномерно распределенная нагрузка q = 50 к. Н/м; • временная эквивалентная нагрузка qv = 36 к. Н/м.

Дано: Требуется проверить прочность бетонной полосы между наклонными сечениями и подобрать диаметр и шаг хомутов в опорной зоне.

Решение: Определим h 0, Rbt и Rsw.

Решение: Определим h 0, Rbt и Rsw. ho = h – a =

Решение: Определим h 0, Rbt и Rsw. ho = h – a = 400 - 30 = 370 мм.

Решение: Определим h 0, Rbt и Rsw. ho = h – a = 400 - 30 = 370 мм. Согласно табл. 5. 2 СП 52 -101 -2003 и п. 5. 1. 10 для В 15
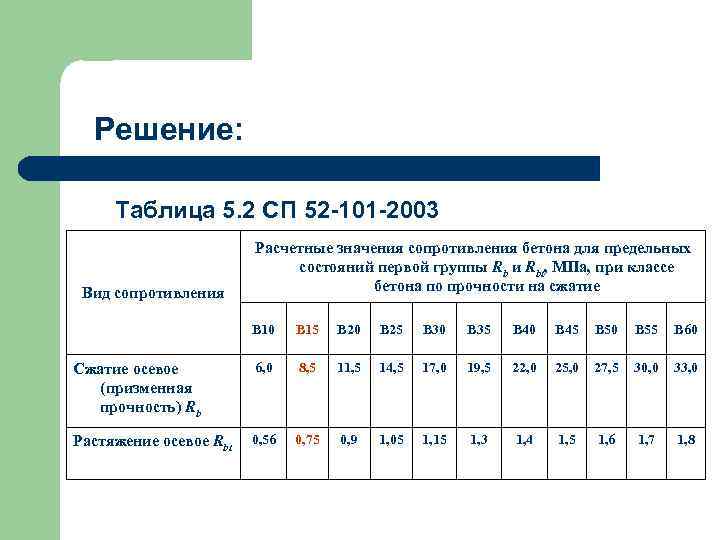
Решение: Таблица 5. 2 СП 52 -101 -2003 Вид сопротивления Расчетные значения сопротивления бетона для предельных состояний первой группы Rb и Rbt, МПа, при классе бетона по прочности на сжатие В 10 B 15 В 20 В 25 В 30 В 35 В 40 В 45 В 50 В 55 В 60 Сжатие осевое (призменная прочность) Rb 6, 0 8, 5 11, 5 14, 5 17, 0 19, 5 22, 0 25, 0 27, 5 30, 0 33, 0 Растяжение осевое Rbt 0, 56 0, 75 0, 9 1, 05 1, 15 1, 3 1, 4 1, 5 1, 6 1, 7 1, 8

Решение: Определим h 0, Rbt и Rsw. ho = h – a = 400 - 30 = 370 мм. Согласно табл. 5. 2 СП 52 -101 -2003 и п. 5. 1. 10 для В 15 Rb = 8, 5 МПа и Rbt = 0, 75 МПа.

Решение: Определим h 0, Rbt и Rsw. ho = h – a = 400 - 30 = 370 мм. Согласно табл. 5. 2 СП 52 -101 -2003 и п. 5. 1. 10 для В 15 Rb = 8, 5 МПа и Rbt = 0, 75 МПа. Согласно табл. 5. 8 СП 52 -101 -2003 и п. 5. 2. 7 для А 240
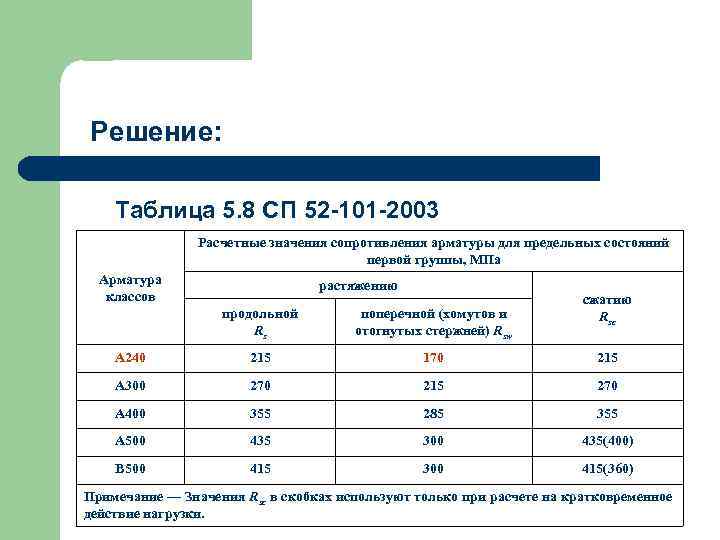
Решение: Таблица 5. 8 СП 52 -101 -2003 Расчетные значения сопротивления арматуры для предельных состояний первой группы, МПа Арматура классов растяжению сжатию Rsc продольной Rs поперечной (хомутов и отогнутых стержней) Rsw А 240 215 170 215 А 300 270 215 270 А 400 355 285 355 А 500 435 300 435(400) В 500 415 300 415(360) Примечание — Значения Rsc в скобках используют только при расчете на кратковременное действие нагрузки.

Решение: Определим h 0, Rbt и Rsw. ho = h – a = 400 - 30 = 370 мм. Согласно табл. 5. 2 СП 52 -101 -2003 и п. 5. 1. 10 для В 15 Rb = 8, 5 МПа и Rbt = 0, 75 МПа. Согласно табл. 5. 8 СП 52 -101 -2003 и п. 5. 2. 7 для А 240 Rsw = 170 МПа.

Решение: Наибольшая поперечная сила в опорном сечении равна
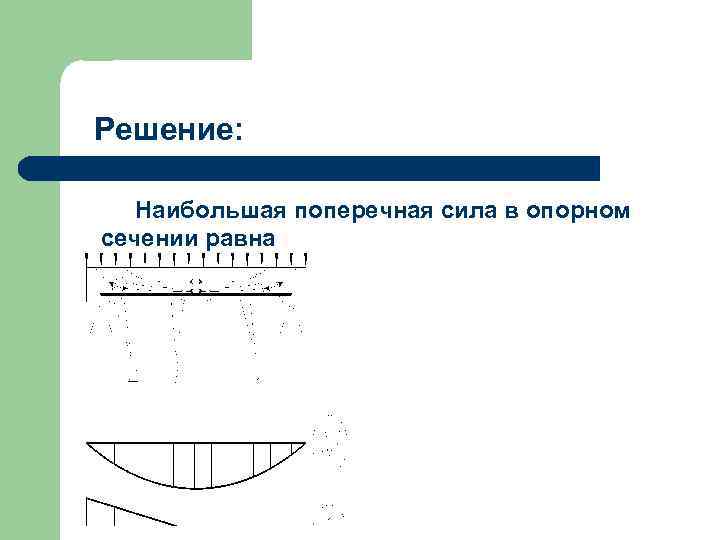
Решение: Наибольшая поперечная сила в опорном сечении равна
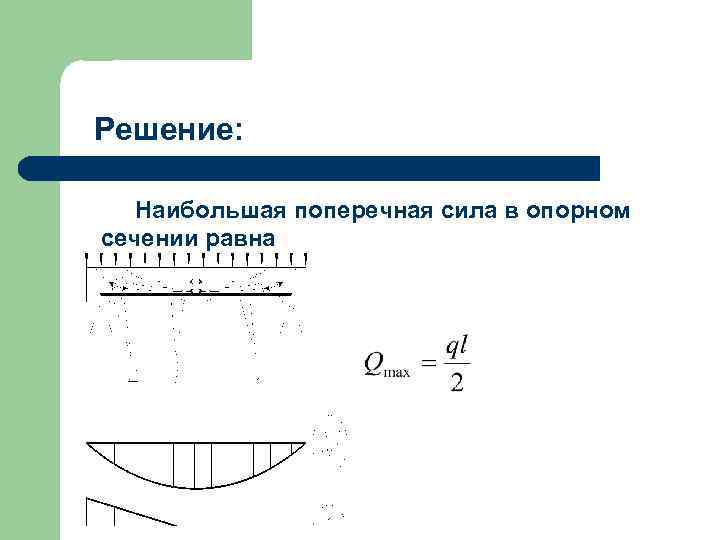
Решение: Наибольшая поперечная сила в опорном сечении равна
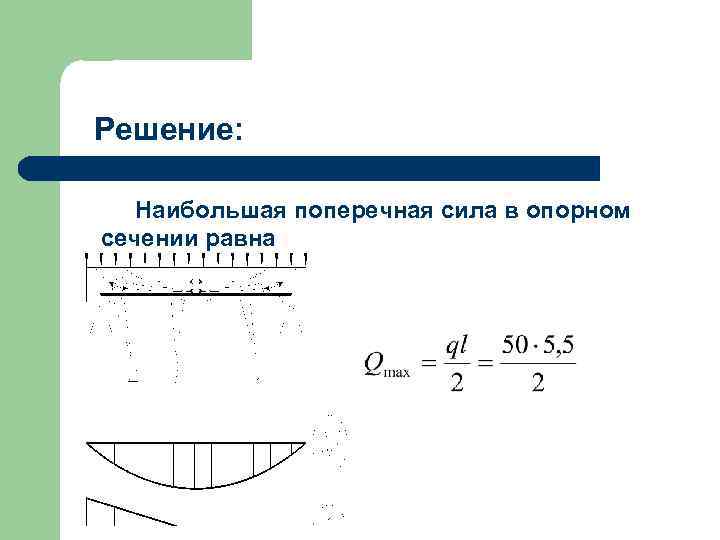
Решение: Наибольшая поперечная сила в опорном сечении равна
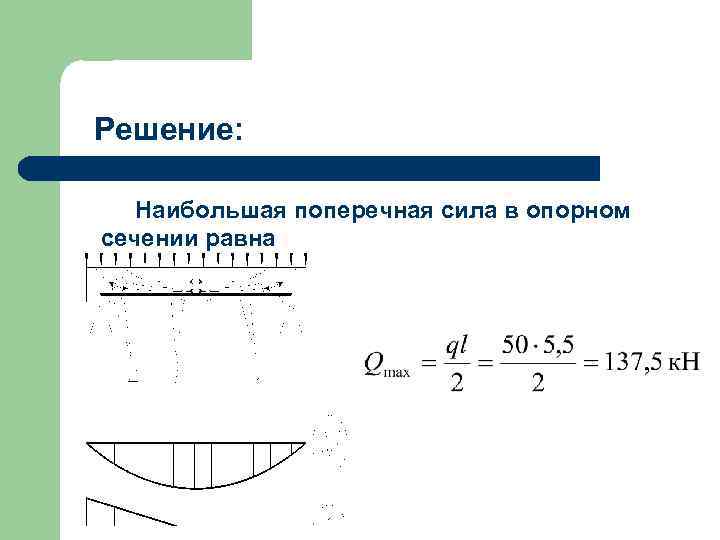
Решение: Наибольшая поперечная сила в опорном сечении равна

Решение: Прочность бетонной полосы проверим из условия 6. 65 СП 52 -101 -2003
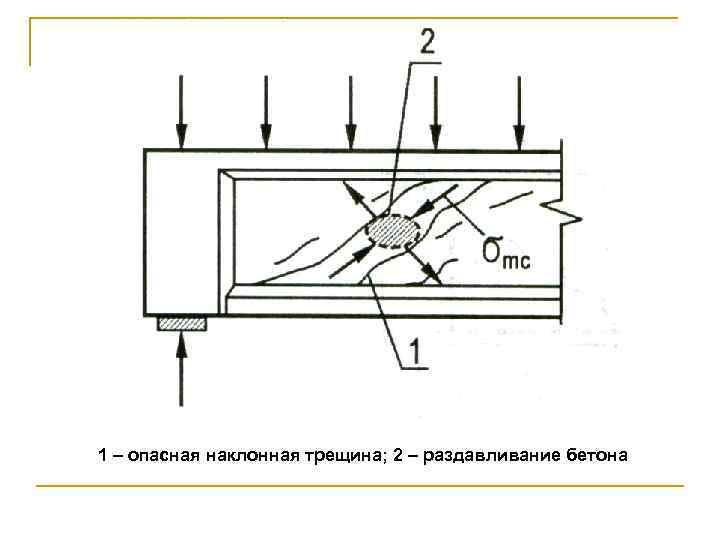
1 – опасная наклонная трещина; 2 – раздавливание бетона

Решение: Прочность бетонной полосы проверим из условия 6. 65 СП 52 -101 -2003 0, 3 Rbbh 0 =

Решение: Прочность бетонной полосы проверим из условия 6. 65 СП 52 -101 -2003 0, 3 Rbbh 0 = 0, 3· 8, 5· 200· 370

Решение: Прочность бетонной полосы проверим из условия 6. 65 СП 52 -101 -2003 0, 3 Rbbh 0 = 0, 3· 8, 5· 200· 370 = 188700 Н

Решение: Прочность бетонной полосы проверим из условия 6. 65 СП 52 -101 -2003 0, 3 Rbbh 0 = 0, 3· 8, 5· 200· 370 = 188700 Н 188, 7 к. Н > Qmax = 137, 5 к. Н,

Решение: Прочность бетонной полосы проверим из условия 6. 65 СП 52 -101 -2003 0, 3 Rbbh 0 = 0, 3· 8, 5· 200· 370 = 188700 Н 188, 7 к. Н > Qmax = 137, 5 к. Н, т. е. прочность полосы обеспечена.

Решение: Расчет изгибаемых элементов с поперечной арматурой и без отгибов на действие поперечной силы по наклонной трещине производят из условия 6. 66 СП

Решение: Расчет изгибаемых элементов с поперечной арматурой и без отгибов на действие поперечной силы по наклонной трещине производят из условия 6. 66 СП
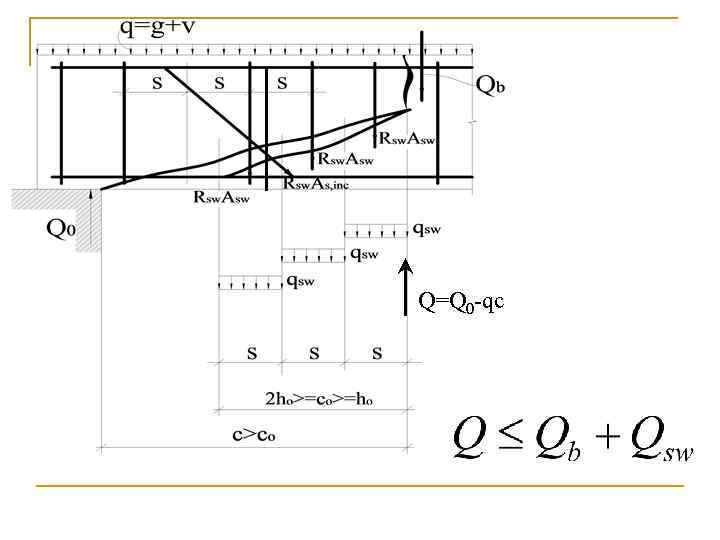
Q=Q 0 -qc

Решение: Поперечную силу Qb определяют по формуле 6. 67 СП

Решение: Поперечную силу Qb определяют по формуле 6. 67 СП

Решение: Поперечную силу Qb определяют по формуле 6. 67 СП но принимают не более 2, 5 Rbt b h 0 и не менее 0, 5 Rbt b h 0;

Решение: Поперечную силу Qb определяют по формуле 6. 67 СП но принимают не более 2, 5 Rbt b h 0 и не менее 0, 5 Rbt b h 0; b 2 - коэффициент, принимаемый равным 1, 5.

Решение: При выполнении условия Q Qb поперечная арматура по расчету не требуется и она ставиться конструктивно в соответствии с п. 8. 3. 10 - 8. 3. 12.

Решение: Расчет элементов без поперечной арматуры на действие поперечной силы производится из условий

Решение: Расчет элементов без поперечной арматуры на действие поперечной силы производится из условий Qmax < 2, 5 Rbtbho где Qmax - максимальная поперечная сила у грани опоры;
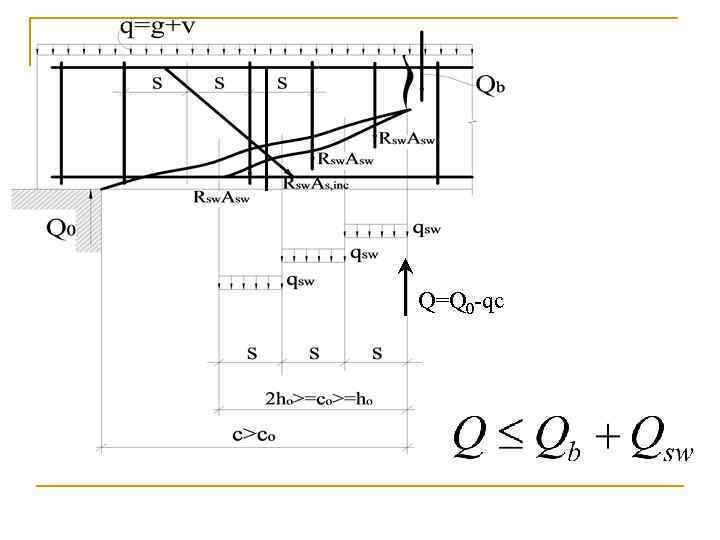
Q=Q 0 -qc

Решение: Расчет элементов без поперечной арматуры на действие поперечной силы производится из условий Qmax < 2, 5 Rbtbho где Qmax - максимальная поперечная сила у грани опоры;

Решение: Расчет элементов без поперечной арматуры на действие поперечной силы производится из условий Qmax < 2, 5 Rbtbho где Qmax - максимальная поперечная сила у грани опоры; где Q - поперечная сила в конце наклонного сечения, начинающегося от опоры;
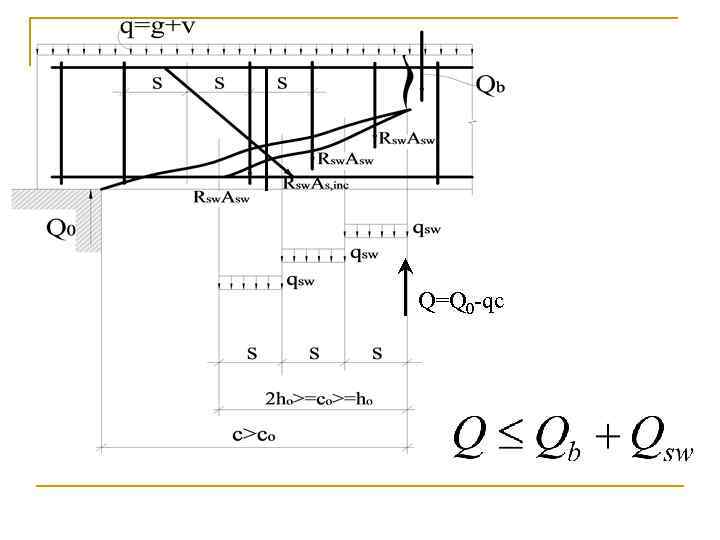
Q=Q 0 -qc

Решение: Расчет элементов без поперечной арматуры на действие поперечной силы производится из условий Qmax < 2, 5 Rbtbho где Qmax - максимальная поперечная сила у грани опоры; где Q - поперечная сила в конце наклонного сечения, начинающегося от опоры; значение с принимается не более сmax = 3 ho

Решение: Проверим первое условие

Решение: Проверим первое условие 2, 5 Rbtbho =

Решение: Проверим первое условие 2, 5 Rbtbho = 2, 5 0, 75 200 370 =

Решение: Проверим первое условие 2, 5 Rbtbho = 2, 5 0, 75 200 370 = 138750 Н

Решение: Проверим первое условие 2, 5 Rbtbho = 2, 5 0, 75 200 370 = 138750 Н 138, 7 к. Н > Qmax = 137, 5 к. Н

Решение: Проверим второе условие

Решение: Проверим второе условие При этом если то с = 3 h 0. ,

Решение: Если то , где q 1 = q – 0, 5 qv или q 1 = g + 0, 5 v

Решение: В нашем случае q 1 = q – 0, 5 qv

Решение: В нашем случае q 1 = q – 0, 5 qv = 50 – 18 = 32 к. Н/м.

Решение: В нашем случае q 1 = q – 0, 5 qv = 50 – 18 = 32 к. Н/м. Rbt b/6 =

Решение: В нашем случае q 1 = q – 0, 5 qv = 50 – 18 = 32 к. Н/м. Rbt b/6 = 0, 75 200/6 =

Решение: В нашем случае q 1 = q – 0, 5 qv = 50 – 18 = 32 к. Н/м. Rbt b/6 = 0, 75 200/6 = 150 H/мм

Решение: В нашем случае q 1 = q – 0, 5 qv = 50 – 18 = 32 к. Н/м. Rbt b/6 = 0, 75 200/6 = 150 H/мм > q 1= 32 Н/мм.

Решение: Если , то с = 3 h 0.

Решение: В нашем случае q 1 = q – 0, 5 qv = 50 – 18 = 32 к. Н/м. Rbt b/6 = 0, 75 200/6 = 150 H/мм > q 1= 32 Н/мм. Тогда c = 3 h 0

Решение: В нашем случае q 1 = q – 0, 5 qv = 50 – 18 = 32 к. Н/м. Rbt b/6 = 0, 75 200/6 = 150 H/мм > q 1= 32 Н/мм. Тогда c = 3 h 0 = 3 370

Решение: В нашем случае q 1 = q – 0, 5 qv = 50 – 18 = 32 к. Н/м. Rbt b/6 = 0, 75 200/6 = 150 H/мм > q 1= 32 Н/мм. Тогда c = 3 h 0 = 3 370 = 1110 мм.

Решение: Проверим второе условие

Решение: Проверим второе условие

Решение: Проверим второе условие

Решение: Проверим второе условие Поскольку Q = Qmax- q 1 c =

Решение: Проверим второе условие Поскольку Q = Qmax- q 1 c = 137, 5 - 32 1, 11 =

Решение: Проверим второе условие Поскольку Q = Qmax- q 1 c = 137, 5 - 32 1, 11 = 102 к. Н

Решение: Проверим второе условие Поскольку Q = Qmax- q 1 c = 137, 5 - 32 1, 11 = 102 к. Н > 27, 7 к. Н,

Решение: Проверим второе условие Поскольку Q = Qmax- q 1 c = 137, 5 - 32 1, 11 = 102 к. Н > 27, 7 к. Н, то поперечная арматура требуется по расчету.
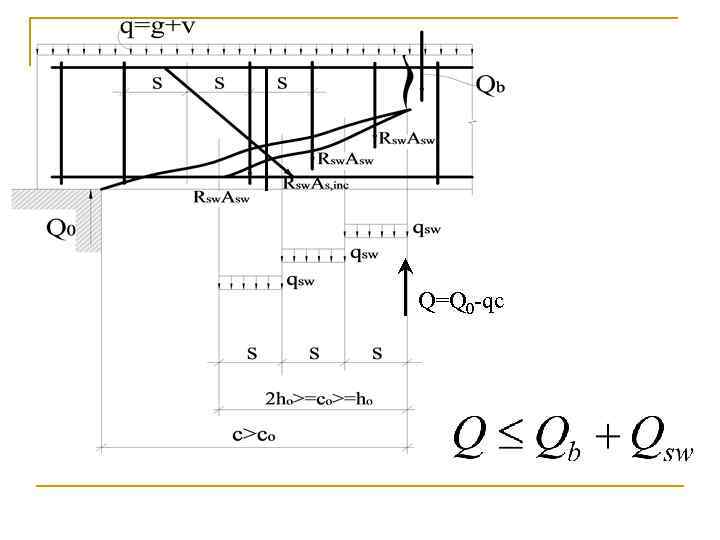
Q=Q 0 -qc

Решение: Усилие Qsw для поперечной арматуры, нормальной к продольной оси элемента, определяют по формуле Qsw = sw qsw c 0, где sw — коэффициент, принимаемый равным 0, 75; cо - длина проекции наклонной трещины, принимаемая равной с, но не более 2 ho;

Решение: qsw — усилие в поперечной арматуре на единицу длины элемента

Решение: qsw — усилие в поперечной арматуре на единицу длины элемента при этом хомуты учитывают в расчете, если соблюдается условие qsw > 0, 25 Rbt b

Решение: Требуемая интенсивность хомутов qsw при действии равномерно распределенной нагрузки определяется в зависимости от следующим образом:

Решение: Требуемая интенсивность хомутов qsw при действии равномерно распределенной нагрузки определяется в зависимости от следующим образом: если Qb 1 ≥ 2 Mb/ho - Qmax , где

Решение: Требуемая интенсивность хомутов qsw при действии равномерно распределенной нагрузки определяется в зависимости от следующим образом: если Qb 1 ≥ 2 Mb/ho - Qmax , где

Решение: если Qb 1 < 2 Mb/ho - Qmax

Решение: если Qb 1 < 2 Mb/ho - Qmax

Решение: При этом, если Qb 1 < Rbtbho,

Решение: В случае, если полученное значение qsw не удовлетворяет условию qsw > 0, 25 Rbt b, его следует вычислять по формуле и принимать не менее

Решение: В нашем случае Мb= 1, 5 Rbtbh 02=

Решение: В нашем случае Мb= 1, 5 Rbtbh 02= 1, 5· 0, 75· 200· 3702=

Решение: В нашем случае Мb= 1, 5 Rbtbh 02= 1, 5· 0, 75· 200· 3702= 30, 8· 106 Н·мм.

Решение: В нашем случае Мb= 1, 5 Rbtbh 02= 1, 5· 0, 75· 200· 3702= 30, 8· 106 Н·мм. Тогда

Решение: В нашем случае Мb= 1, 5 Rbtbh 02= 1, 5· 0, 75· 200· 3702= 30, 8· 106 Н·мм. Тогда

Решение: В нашем случае Мb= 1, 5 Rbtbh 02= 1, 5· 0, 75· 200· 3702= 30, 8· 106 Н·мм. Тогда

Решение: В нашем случае Мb= 1, 5 Rbtbh 02= 1, 5· 0, 75· 200· 3702= 30, 8· 106 Н·мм. Тогда

Решение: В нашем случае Мb= 1, 5 Rbtbh 02= 1, 5· 0, 75· 200· 3702= 30, 8· 106 Н·мм. Тогда Так как 2 Мb/ho- Qmax=

Решение: В нашем случае Мb= 1, 5 Rbtbh 02= 1, 5· 0, 75· 200· 3702= 30, 8· 106 Н·мм. Тогда Так как 2 Мb/ho- Qmax= 2· 30, 8· 106/370 - 137500=

Решение: В нашем случае Мb= 1, 5 Rbtbh 02= 1, 5· 0, 75· 200· 3702= 30, 8· 106 Н·мм. Тогда Так как 2 Мb/ho- Qmax= 2· 30, 8· 106/370 - 137500= = 28986 Н

Решение: В нашем случае Мb= 1, 5 Rbtbh 02= 1, 5· 0, 75· 200· 3702= 30, 8· 106 Н·мм. Тогда Так как 2 Мb/ho- Qmax= 2· 30, 8· 106/370 - 137500= = 28986 Н < Qb 1= 62790 H, то

Решение: В нашем случае Мb= 1, 5 Rbtbh 02= 1, 5· 0, 75· 200· 3702= 30, 8· 106 Н·мм. Тогда Так как 2 Мb/ho- Qmax= 2· 30, 8· 106/370 - 137500= = 28986 Н < Qb 1= 62790 H, то

Решение: В нашем случае

Решение: В нашем случае

Решение: В нашем случае

Решение: Согласно п. 8. 3. 11 СП шаг хомутов ssw

Решение: Согласно п. 8. 3. 11 СП шаг хомутов ssw опоры должен быть не более ho/2 = 185 и более 300 мм,

Решение: Согласно п. 8. 3. 11 СП шаг хомутов ssw опоры должен быть не более ho/2 = 185 и более 300 мм, а в пролете - 0, 75 ho = 271 и 500 мм.

Решение: Согласно п. 8. 3. 11 СП шаг хомутов ssw опоры должен быть не более ho/2 = 185 и более 300 мм, а в пролете - 0, 75 ho = 271 и 500 мм. Максимально допустимый шаг у опоры согласно п. 6. 2. 34

Решение: Согласно п. 8. 3. 11 СП шаг хомутов ssw опоры должен быть не более ho/2 = 185 и более 300 мм, а в пролете - 0, 75 ho = 271 и 500 мм. Максимально допустимый шаг у опоры согласно п. 6. 2. 34

Решение: Принимаем шаг хомутов у опоры sw 1= 150 мм,

Решение: Принимаем шаг хомутов у опоры sw 1= 150 мм, а в пролете 250 мм.

Решение: Принимаем шаг хомутов у опоры sw 1= 150 мм, а в пролете 250 мм. Отсюда

Решение: Принимаем шаг хомутов у опоры sw 1= 150 мм, а в пролете 250 мм. Отсюда

Решение: Принимаем шаг хомутов у опоры sw 1= 150 мм, а в пролете 250 мм. Отсюда

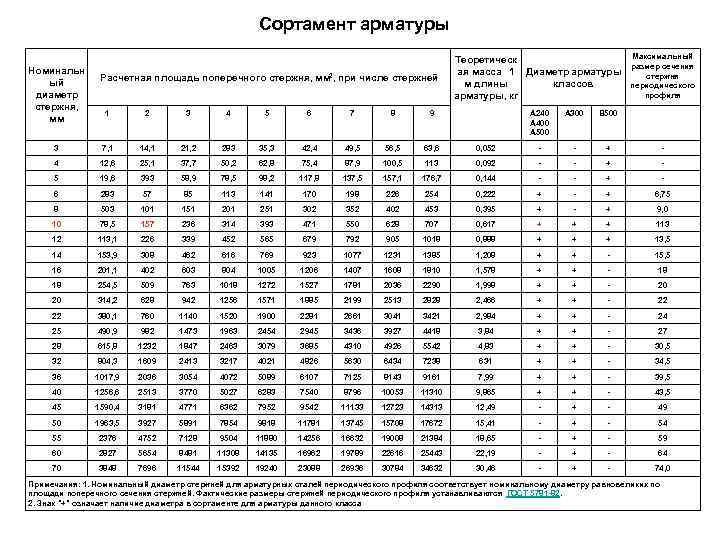
Решение: Принимаем в поперечном сечении два хомута по 10 мм
Сортамент арматуры Номинальн ый диаметр стержня, мм Расчетная площадь поперечного стержня, мм 2, при числе стержней 1 2 3 4 5 6 7 8 9 3 7, 1 14, 1 21, 2 283 35, 3 42, 4 49, 5 56, 5 63, 6 4 12, 6 25, 1 37, 7 50, 2 62, 8 75, 4 87, 9 100, 5 5 19, 6 393 58, 9 78, 5 98, 2 117, 8 137, 5 6 283 57 85 113 141 170 8 503 101 151 201 251 302 10 78, 5 157 236 314 393 12 113, 1 226 339 452 14 153, 9 308 462 16 201, 1 402 18 254, 5 20 314, 2 22 Теоретическ ая масса 1 Диаметр арматуры м длины классов арматуры, кг Максимальный размер сечения стержня периодического профиля А 240 А 400 А 500 A 300 В 500 0, 052 - - + - 113 0, 092 - - + - 157, 1 176, 7 0, 144 - - + - 198 226 254 0, 222 + - + 6, 75 352 402 453 0, 395 + - + 9, 0 471 550 628 707 0, 617 + + + 113 565 679 792 905 1018 0, 888 + + + 13, 5 616 769 923 1077 1231 1385 1, 208 + + - 15, 5 603 804 1005 1206 1407 1608 1810 1, 578 + + - 18 509 763 1018 1272 1527 1781 2036 2290 1, 998 + + - 20 628 942 1256 1571 1885 2199 2513 2828 2, 466 + + - 22 380, 1 760 1140 1520 1900 2281 2661 3041 3421 2, 984 + + - 24 25 490, 9 982 1473 1963 2454 2945 3436 3927 4418 3, 84 + + - 27 28 615, 8 1232 1847 2463 3079 3685 4310 4926 5542 4, 83 + + - 30, 5 32 804, 3 1609 2413 3217 4021 4826 5630 6434 7238 631 + + - 34, 5 36 1017, 9 2036 3054 4072 5089 6107 7125 8143 9161 7, 99 + + - 39, 5 40 1256, 6 2513 3770 5027 6283 7540 8796 10053 11310 9, 865 + + - 43, 5 45 1590, 4 3181 4771 6362 7952 9542 11133 12723 14313 12, 49 - + - 49 50 1963, 5 3927 5891 7854 9818 11781 13745 15708 17672 15, 41 - + - 54 55 2376 4752 7128 9504 11880 14256 16632 19008 21384 18, 65 - + - 59 60 2827 5654 8481 11308 14135 16962 19789 22616 25443 22, 19 - + - 64 70 3848 7696 11544 15392 19240 23088 26936 30784 34632 30, 46 - + - 74, 0 Примечания: 1. Номинальный диаметр стержней для арматурных сталей периодического профиля соответствует номинальному диаметру равновеликих по площади поперечного сечения стержней. Фактические размеры стержней периодического профиля устанавливаются ГОСТ 5781 -82. 2. Знак "+" означает наличие диаметра в сортаменте для арматуры данного класса

Решение: Принимаем в поперечном сечении два хомута по 10 мм (Asw = 157 мм 2).

Решение: Таким образом, принятая интенсивность хомутов у опоры и в пролете соответственно равны:

Решение: Таким образом, принятая интенсивность хомутов у опоры и в пролете соответственно равны:

Решение: Таким образом, принятая интенсивность хомутов у опоры и в пролете соответственно равны:

Решение: Таким образом, принятая интенсивность хомутов у опоры и в пролете соответственно равны:

Решение: Таким образом, принятая интенсивность хомутов у опоры и в пролете соответственно равны:

Решение: Таким образом, принятая интенсивность хомутов у опоры и в пролете соответственно равны:

Решение: Проверим условие qsw 0, 25 Rbt b

Решение: Проверим условие qsw 0, 25 Rbt b 0, 25 Rbtb =

Решение: Проверим условие qsw 0, 25 Rbt b 0, 25 Rbtb = 0, 25· 0, 75· 200

Решение: Проверим условие qsw 0, 25 Rbt b 0, 25 Rbtb = 0, 25· 0, 75· 200 = 37, 5 Н/мм

Решение: Проверим условие qsw 0, 25 Rbt b 0, 25 Rbtb = 0, 25· 0, 75· 200 = 37, 5 Н/мм < qsw 1

Решение: Проверим условие qsw 0, 25 Rbt b 0, 25 Rbtb = 0, 25· 0, 75· 200 = 37, 5 Н/мм < qsw 1 и 37, 5 < qsw 2.

Решение: Проверим условие

Решение: Проверим условие

Решение: При этом невыгоднейшее значение с принимают

Решение: При этом невыгоднейшее значение с принимают а если при этом

Решение: При этом невыгоднейшее значение с принимают а если при этом или

Решение: При этом невыгоднейшее значение с принимают а если при этом или

Решение: Поскольку

Решение: Поскольку

Решение: Поскольку

Решение: Поскольку

Решение: Поскольку

Решение: Поскольку

Решение: Поскольку

Решение: Поскольку

Решение: Поскольку

Решение: Принимаем c 0 = c = 431, 49 мм.

Решение: Принимаем c 0 = c = 431, 49 мм. Тогда

Решение: Принимаем c 0 = c = 431, 49 мм. Тогда

Решение: Принимаем c 0 = c = 431, 49 мм. Тогда

Решение: Принимаем c 0 = c = 431, 49 мм. Тогда

Решение: Принимаем c 0 = c = 431, 49 мм. Тогда

Решение: Таким образом, арматура подобрана верно.
ПрактикаЖБК-41.ppt