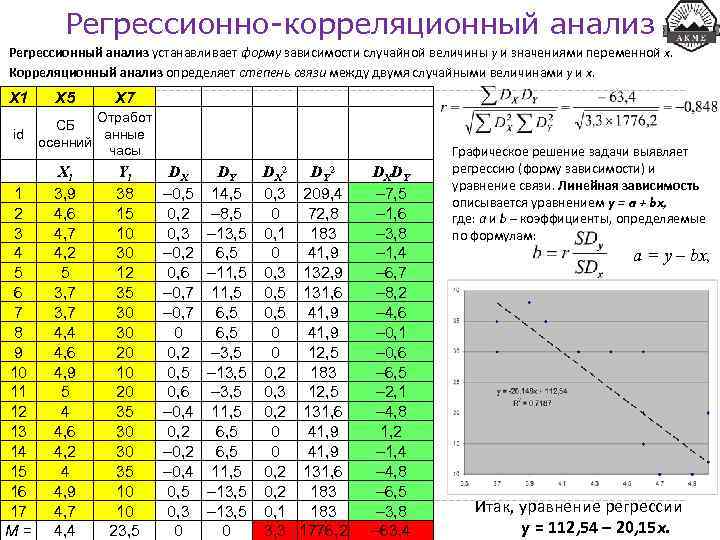
 Регрессионно-корреляционный анализ Регрессионный анализ устанавливает форму зависимости случайной величины y и значениями переменной x. Корреляционный анализ определяет степень связи между двумя случайными величинами y и x. X 1 id 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 М = X 5 X 7 Отработ СБ анные осенний часы Xi 3, 9 4, 6 4, 7 4, 2 5 3, 7 4, 4 4, 6 4, 9 5 4 4, 6 4, 2 4 4, 9 4, 7 4, 4 Yi 38 15 10 30 12 35 30 30 20 10 20 35 30 30 35 10 10 23, 5 DX – 0, 5 0, 2 0, 3 – 0, 2 0, 6 – 0, 7 0 0, 2 0, 5 0, 6 – 0, 4 0, 2 – 0, 4 0, 5 0, 3 0 DY 14, 5 – 8, 5 – 13, 5 6, 5 – 11, 5 6, 5 – 3, 5 – 13, 5 – 3, 5 11, 5 6, 5 11, 5 – 13, 5 0 DX 2 DY 2 0, 3 209, 4 0 72, 8 0, 1 183 0 41, 9 0, 3 132, 9 0, 5 131, 6 0, 5 41, 9 0 12, 5 0, 2 183 0, 3 12, 5 0, 2 131, 6 0 41, 9 0, 2 131, 6 0, 2 183 0, 1 183 3, 3 1776, 2 DXDY – 7, 5 – 1, 6 – 3, 8 – 1, 4 – 6, 7 – 8, 2 – 4, 6 – 0, 1 – 0, 6 – 6, 5 – 2, 1 – 4, 8 1, 2 – 1, 4 – 4, 8 – 6, 5 – 3, 8 – 63, 4 Графическое решение задачи выявляет регрессию (форму зависимости) и уравнение связи. Линейная зависимость описывается уравнением y = a + bx, где: а и b – коэффициенты, определяемые по формулам: a = y – bx, Итак, уравнение регрессии y = 112, 54 – 20, 15 x.
Регрессионно-корреляционный анализ Регрессионный анализ устанавливает форму зависимости случайной величины y и значениями переменной x. Корреляционный анализ определяет степень связи между двумя случайными величинами y и x. X 1 id 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 М = X 5 X 7 Отработ СБ анные осенний часы Xi 3, 9 4, 6 4, 7 4, 2 5 3, 7 4, 4 4, 6 4, 9 5 4 4, 6 4, 2 4 4, 9 4, 7 4, 4 Yi 38 15 10 30 12 35 30 30 20 10 20 35 30 30 35 10 10 23, 5 DX – 0, 5 0, 2 0, 3 – 0, 2 0, 6 – 0, 7 0 0, 2 0, 5 0, 6 – 0, 4 0, 2 – 0, 4 0, 5 0, 3 0 DY 14, 5 – 8, 5 – 13, 5 6, 5 – 11, 5 6, 5 – 3, 5 – 13, 5 – 3, 5 11, 5 6, 5 11, 5 – 13, 5 0 DX 2 DY 2 0, 3 209, 4 0 72, 8 0, 1 183 0 41, 9 0, 3 132, 9 0, 5 131, 6 0, 5 41, 9 0 12, 5 0, 2 183 0, 3 12, 5 0, 2 131, 6 0 41, 9 0, 2 131, 6 0, 2 183 0, 1 183 3, 3 1776, 2 DXDY – 7, 5 – 1, 6 – 3, 8 – 1, 4 – 6, 7 – 8, 2 – 4, 6 – 0, 1 – 0, 6 – 6, 5 – 2, 1 – 4, 8 1, 2 – 1, 4 – 4, 8 – 6, 5 – 3, 8 – 63, 4 Графическое решение задачи выявляет регрессию (форму зависимости) и уравнение связи. Линейная зависимость описывается уравнением y = a + bx, где: а и b – коэффициенты, определяемые по формулам: a = y – bx, Итак, уравнение регрессии y = 112, 54 – 20, 15 x.