Практическая работа по математике тема: «Показательные уравнения. Показательные неравенства. Система показательных уравнений. » Работу выполнили Студенты 2 курса гр. С-142 Цой М. А. и Иванова О. А.
Содержание: • Введение. • Типы показательных уравнений и методы решения. • Типы показательных неравенств и методы решения. • Типы систем показательных уравнений и методы решения. • Заключение.
Введение В школьном курсе математики важное место отводится решению показательных уравнений и неравенств и системам, содержащие показательные уравнения. Впервые ученики встречаются с показательными уравнениями и неравенствами в 10 классе, после того, как познакомятся с показательной функцией и ее свойствами, а системы, содержащие показательные уравнения и неравенства в 11 классе. Показательные уравнения, неравенства, системы, содержащие показательные уравнения, встречаются в заданиях ЕГЭ. Поэтому изучению методов их решения должно быть уделено значительное внимание, т. к. в заданиях ЕГЭ системы, содержащие показательные уравнения и неравенства могут быть и комбинированными. И для того, чтобы решить правильно систему уравнений или неравенств, нужно правильно решить показательное уравнение или неравенство. При решении показательных уравнений и неравенств часто возникают трудности, связанные со следующими особенностями: - незнание четкого алгоритма решения показательных уравнений, неравенств и их систем; - при решении показательных уравнений и неравенств, ученики производят преобразования, которые не равносильны исходным уравнениям и неравенствам; - при решении показательного уравнения и неравенства введением новой переменной забывают возвращаться к обратной замене. Вышесказанное определяет актуальность выбранной темы и полезность ее изучения для будущей педагогической практики. Цель данной работы: изучить теоретический материал по теме, проанализировать данную тему в учебниках по алгебре и началам анализа, систематизировать задания ЕГЭ на решение показательных уравнений и 4 неравенств, систематизировать и обобщить методические рекомендации по решению показательных уравнений и неравенств. Для достижения поставленной цели необходимо решить следующие задачи: - изучить требования государственных стандартов по теме «Показательные уравнения и неравенства» ; - - проанализировать материал по теме в учебниках алгебры и начал анализа; - - систематизировать методы решения показательных уравнений и неравенств; - - систематизировать и обобщить методические особенности изучения данной темы.
Показательные уравнения и методы их решения. Решение множества показательных уравнений не обходится без замен, квадратных уравнений и сложных преобразований. Приведенные ниже примеры помогут Вам в этом быстро разобраться и научат решать самые сложные из них. Также Вы сможете выучить некоторые свойства логарифмов без которых показательные уравнения в простой способ не решить. Начнем с самых азов - теоретического материала об уравнениях. Показательными называют уравнения в которых неизвестная величина содержится в показателе степени, при этом основа степени не содержит неизвестной величины. Самое простое показательных уравнения ax=b решают логарифмированием x=log[a](b).
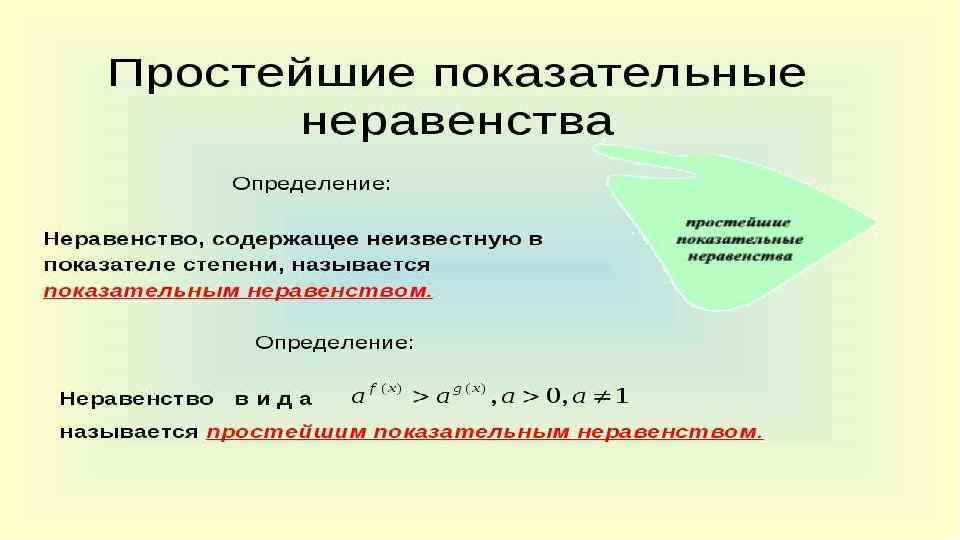
Типы показательных неравенств и методы их решения. • Простейшие показательные неравенства • Определение: Неравенство, содержащее неизвестную в показателе степени, называется показательным неравенством. • Определение: Неравенство в и д а называется простейшим показательным неравенством.
Типы систем показательных уравнений и методы решения. • Что является обязательным при решении системы показательных уравнений? Конечно, преобразование данной системы в систему простейших уравнений. • Решить системы уравнений: Выразим у через х из (2) -го уравнения системы и подставим это значение в (1) -ое уравнение системы. Решаем (2) -ое уравнение полученной системы: 2 х+2 x+2=10, применяем формулу: ax+y=ax∙ay. 2 x+2 x∙ 22=10, вынесем общий множитель 2 х за скобки: 2 х(1+22)=10 или 2 х∙ 5=10, отсюда 2 х=21, отсюда х=1. Возвращаемся к системе уравнений. Ответ : (1; 2)
Решение. Представляем левую и правую части (1) -го уравнения в виде степеней с основанием 2, а правую часть (2) -го уравнения как нулевую степень числа 5. Если равны две степени с одинаковыми основаниями, то равны и показатели этих степеней — приравниваем показатели степеней с основаниями 2 и показатели степеней с основаниями 5. Получившуюся систему линейных уравнений с двумя переменными решаем методом сложения. Находим х=2 и это значение подставляем вместо х во второе уравнение системы. Находим у. Ответ: (2; 1, 5).
Заключение. Математика, как и любая другая наука не стоит на месте, вместе с развитием общества меняются и взгляды людей, возникают новые мысли и идеи. И XX век не стал в этом смысле исключением. Появление компьютеров внесло свои корректировки в способы решения уравнений и значительно их облегчило. Но компьютер не всегда может быть под рукой (экзамен, контрольная), поэтому знание хотя бы самых главных способов решения уравнений необходимо знать. Использование уравнений в повседневной жизни – редкость. Они нашли свое применение во многих отраслях хозяйства и практически во всех новейших технологиях. В данной работе были представлены далеко не все, способы решения уравнений и даже не все их виды, а только самые основные. Я надеюсь, что мое сочинение может послужить неплохим справочным материалом при решении тех или иных уравнений. В заключении хотелось бы отметить, что при написании данного сочинения я не ставил себе цели показать все виды уравнений, а излагал лишь имеющийся у меня материал.
Скачать презентацию Практическая работа по математике тема Показательные уравнения Показательные
Цой М. - Показательные уравнения.Показательные неравенства.Система показательных уравнений..pptx