Pragmatic approaches to image resampling Tom Mc Glynn

Pragmatic approaches to image resampling Tom Mc. Glynn NASA/GSFC

Outline o o o Why do we resample? Isn’t resampling a solved problem? Some approaches to resampling. n o A new algorithm for exact-area resampling using clipping. How should astronomers choose resampling algorithms? Tom Mc. Glynn IPAM Workshop Jan 27, 2004

Why do we need to resample? o Display – transform image into ‘standard’ form n n n Undo warps and distortions Transform to standard frame Resizing o n o Similar operations as in display, but final frame may not be ‘standard’ Mosaicking n o Rotation Image comparison – transform one image to match another n o Magnification and minification Building sky region and all sky images Image arithmetic n Dither additions, image differencing, speckle analysis o Can have most extreme requirements on accuracy of reconstruction but often involves very similar images. Different problems levy different requirements for accuracy and robustness. Many resampling problems involve substantial changes in geometry. Tom Mc. Glynn IPAM Workshop Jan 27, 2004

Resampling examples Sky. View transforms the EGRET all sky map in Galactic coordinates to Equatorial coordinates. Tom Mc. Glynn IPAM Workshop Jan 27, 2004

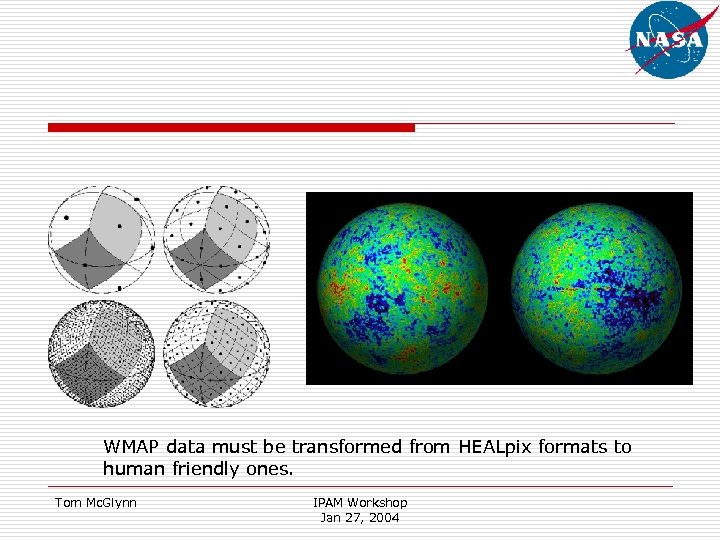WMAP data must be transformed from HEALpix formats to human friendly ones. Tom Mc. Glynn IPAM Workshop Jan 27, 2004

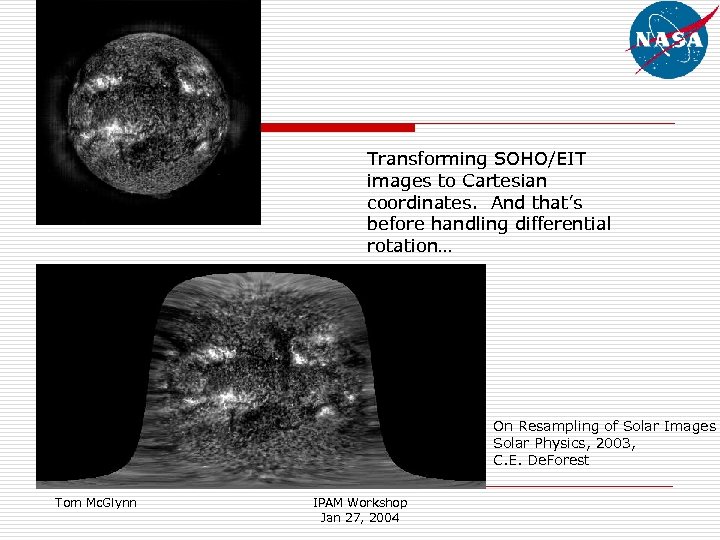Transforming SOHO/EIT images to Cartesian coordinates. And that’s before handling differential rotation… On Resampling of Solar Images Solar Physics, 2003, C. E. De. Forest Tom Mc. Glynn IPAM Workshop Jan 27, 2004

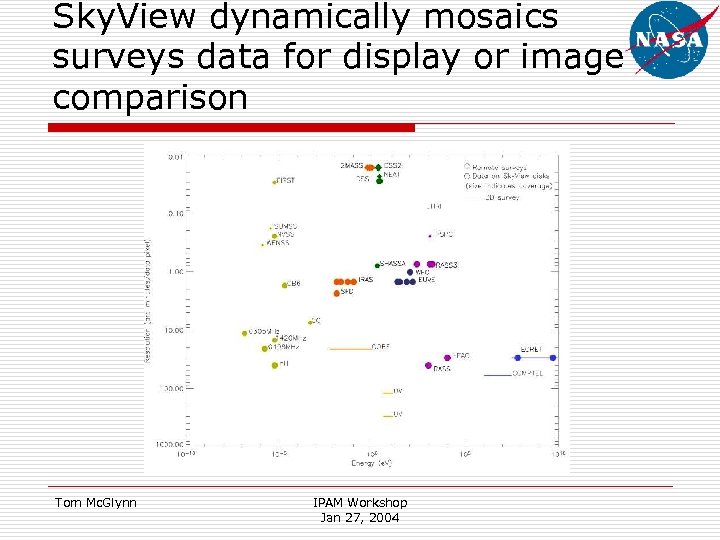Sky. View dynamically mosaics surveys data for display or image comparison Tom Mc. Glynn IPAM Workshop Jan 27, 2004

Sky. Morph image addition. Three co-added NEAT images taken at 20 minute intervals. (1999 discovery images for asteroid 9460) DSS image (1950) Adding NEAT images for asteroid discovery using Sky. Morph. Other survey datasets can also be searched for pre-discovery Tom Mc. Glynn IPAM Workshop Jan 27, 2004

Classical image resampling 1. Image reconstruction The continuous image is regenerated by some method, often by interpolating between the grid point by using an interpolation kernel. 2. Sampling The new grid is constructed by sampling the reconstructed function appropriately. 3. Filters and transformations Intermediate filters and transformations may be applied at various points in the process. Tom Mc. Glynn IPAM Workshop Jan 27, 2004

Ideal Reconstruction o A band-limited function can be exactly reconstructed by convolution with the appropriate kernel. Tom Mc. Glynn IPAM Workshop Jan 27, 2004

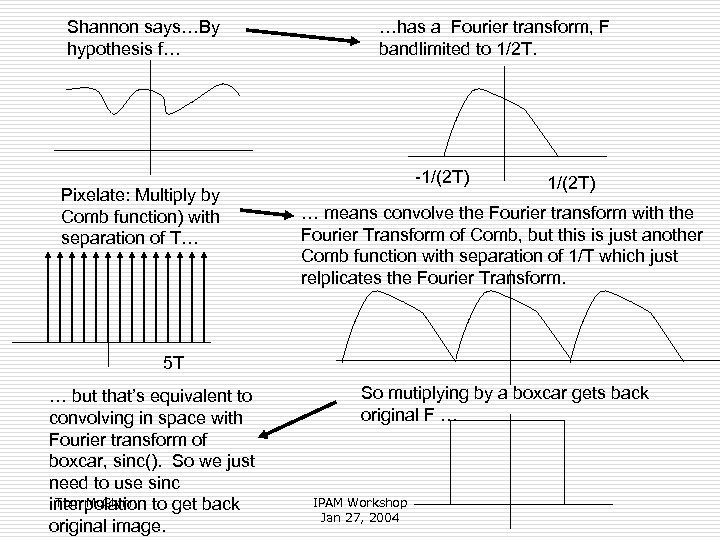Shannon says…By hypothesis f… Pixelate: Multiply by Comb function) with separation of T… …has a Fourier transform, F bandlimited to 1/2 T. -1/(2 T) … means convolve the Fourier transform with the Fourier Transform of Comb, but this is just another Comb function with separation of 1/T which just relplicates the Fourier Transform. 5 T … but that’s equivalent to convolving in space with Fourier transform of boxcar, sinc(). So we just need to use sinc Tom Mc. Glynn interpolation to get back original image. So mutiplying by a boxcar gets back original F … IPAM Workshop Jan 27, 2004

Solved problem? o So sinc function is the optimal filter. Just reconstruct the image using sinc interpolation and resample as needed! Tom Mc. Glynn IPAM Workshop Jan 27, 2004

But… real images are finite o o Chips typically have 1 -4 K pixels with larger detectors using arrays of chips. Edge effects need to be considered … n o o Copying image, image reversal, constant value, 0 beyond edge How do we handle missing pixels? Typical CD song has ~100 K samples before we begin hearing the music. Tom Mc. Glynn IPAM Workshop Jan 27, 2004

…Is the image well sampled? o o Is sampling rate adequate? How do we tell? What can cause high frequencies? n n n Noise and photon statistics Features Processing o n The sky o o Filtering and compression – flat can mean high frequencies. 1 Gigapixel Nyquist-sampled image for 0. 001” resolution covers only 16”. Do users prefilter images? Tom Mc. Glynn IPAM Workshop Jan 27, 2004

…The sky isn’t a plane o Proper basis for sphere is spherical harmonics. n n o o CMB studies use HEALPix pixels to make this easier. Are HTM grids going to be used? Derivation of sinc function kernel assumes rectangular grid. Other functions are appropriate for other samplings. What are the effects of ignoring curvature? Tom Mc. Glynn IPAM Workshop Jan 27, 2004

…Point versus Area resampling o o Pixels have finite extent. In 2 -d case the relationship between the original and resampling pixels can be complex. n n o 1 -D and 2 -D resampling share ‘calculus’ but 2 -D geometry is more complex. If input and output pixels are similar we can presume the function being reconstructed is the flux convolved with the pixel mask. How do we handle resampling pixels with complex shapes? Tom Mc. Glynn IPAM Workshop Jan 27, 2004

What makes resampling hard? o Calculus n n n o Undersampling Noise, features, missing pixels Constraints on the output range (avoidance of negative values, integer valued functions) Geometry n n Differing projections and coordinate systems and orientations. Scale changes Non rectangular pixels. Variations over the image Tom Mc. Glynn IPAM Workshop Jan 27, 2004

Alternatives o Image regeneration n Is the image a derived product? o o o Pixels added? Models? Retake the image Adapt requirements to minimize projection issues Often not feasible or desirable. Tom Mc. Glynn IPAM Workshop Jan 27, 2004

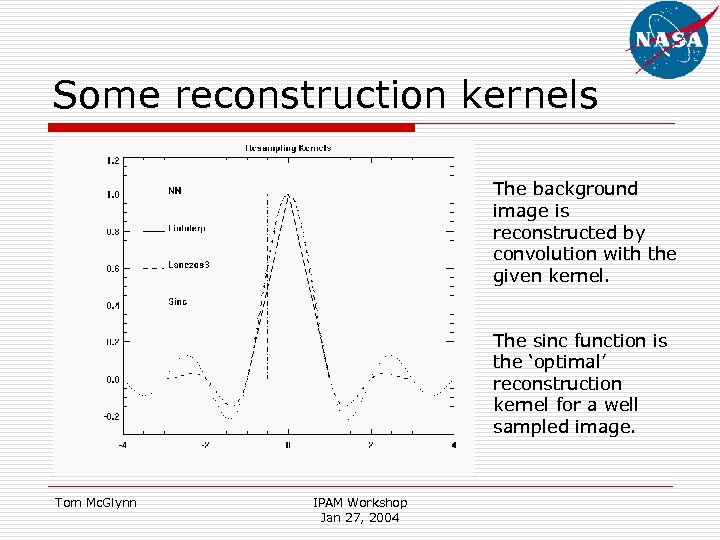Some reconstruction kernels The background image is reconstructed by convolution with the given kernel. The sinc function is the ‘optimal’ reconstruction kernel for a well sampled image. Tom Mc. Glynn IPAM Workshop Jan 27, 2004

Nearest Neighbor Universally panned… o Bad geometric distortions o Suspect photometry o Poor for magnification but even the least elegant techniques may have their place. o Fast o Histogram of values can be preserved. o Sometimes exactly invertible. o Integers stay integers n n o Classifications (does vegetation+water=city) Photon counting algorithms Retention of discontinuities n Man-made boundaries o Constellation maps Tom Mc. Glynn IPAM Workshop Jan 27, 2004

Bilinear Interpolation Fast o Better at preserving astrometry and photometry But o Smooths and blurs the image o Tom Mc. Glynn IPAM Workshop Jan 27, 2004

‘Higher order’ interpolation Best job reproducing well sampled images o Limits blurring But… o Sometimes slower o Can be sensitive to ‘features’ or undersampling. o - negative values when resampling. o o Harder to handle missing pixels Gazillions of choices n n Interpolating or approximating Polynomial approximations o o n n o Splines Local support polynomials Truncated sinc Windowed sinc: Lanczos, Hamming, … Image support for calculation of kernel Image support for resampling calculations Very high order methods (e. g. , exact sinc) can be very slow Tom Mc. Glynn IPAM Workshop Jan 27, 2004

More choices: Interpolation versus Redistribution o o Interpolation n Output flux at a pixel is computed as a sum of weighted input pixels using reconstruction kernel. n Tends to assure differential properties of image (continuity, derivatives) Redistribution (Drizzle, exact area sampling) n Input pixel’s flux is distributed over output pixels using redistribution kernel. n Can ensure integral properties of image (flux or flat field). n Easy to handle missing pixels or other discontinuities n Global integrals can be conserved to the limits of arithmetic precision Tom Mc. Glynn IPAM Workshop Jan 27, 2004

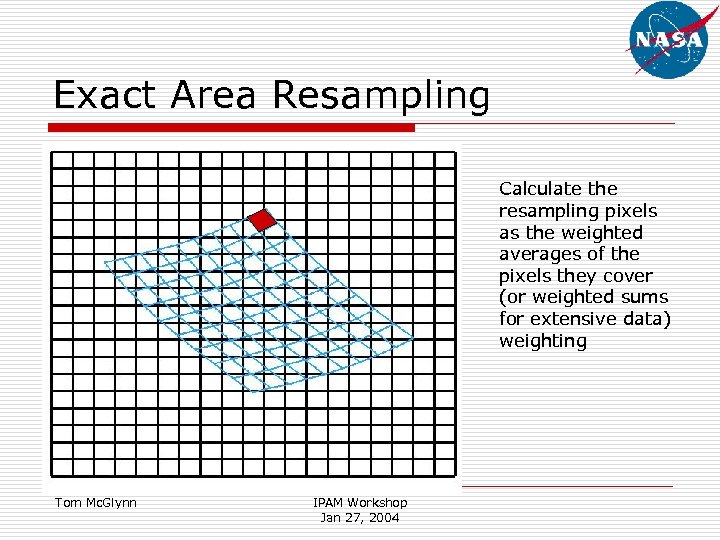Exact Area Resampling Calculate the resampling pixels as the weighted averages of the pixels they cover (or weighted sums for extensive data) weighting Tom Mc. Glynn IPAM Workshop Jan 27, 2004

Approaches o o o Delaunay Triangulation n Using suitable collection of points one finds a set of triangles where each triangle belongs to just one input and output pixel. n Hideously slow… Girard’s theorem (Montage: Berriman and Good) n Work on the celestial sphere and use Girard’s theorem to calculate area – a `practical’ example of using parallel transport of vectors. n Very, very slow. Clipping n How much of the resampling pixels can you view through the window of the input pixels? n Comparable speed to other high-order methods. n Equivalent to algorithm used within Drizzle? Tom Mc. Glynn IPAM Workshop Jan 27, 2004

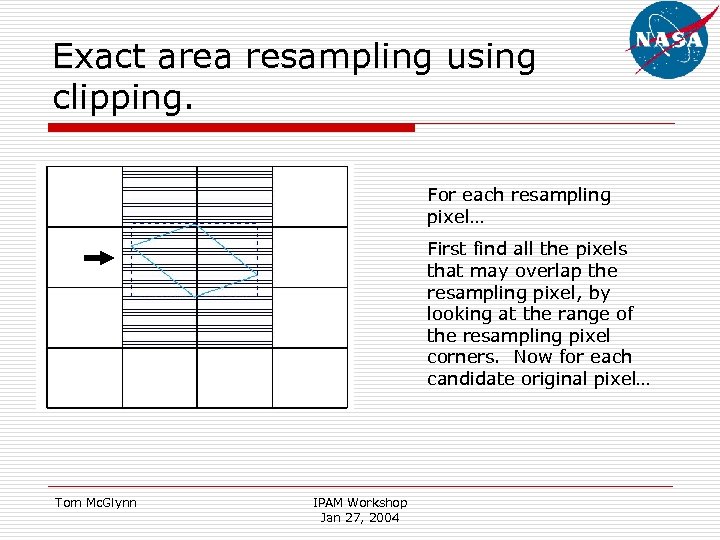Exact area resampling using clipping. For each resampling pixel… First find all the pixels that may overlap the resampling pixel, by looking at the range of the resampling pixel corners. Now for each candidate original pixel… Tom Mc. Glynn IPAM Workshop Jan 27, 2004

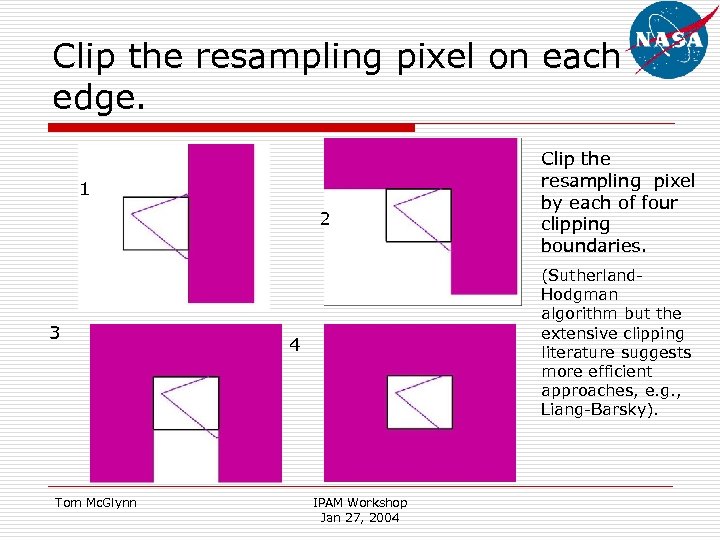Clip the resampling pixel on each edge. 1 2 3 Tom Mc. Glynn Clip the resampling pixel by each of four clipping boundaries. (Sutherland. Hodgman algorithm but the extensive clipping literature suggests more efficient approaches, e. g. , Liang-Barsky). 4 IPAM Workshop Jan 27, 2004

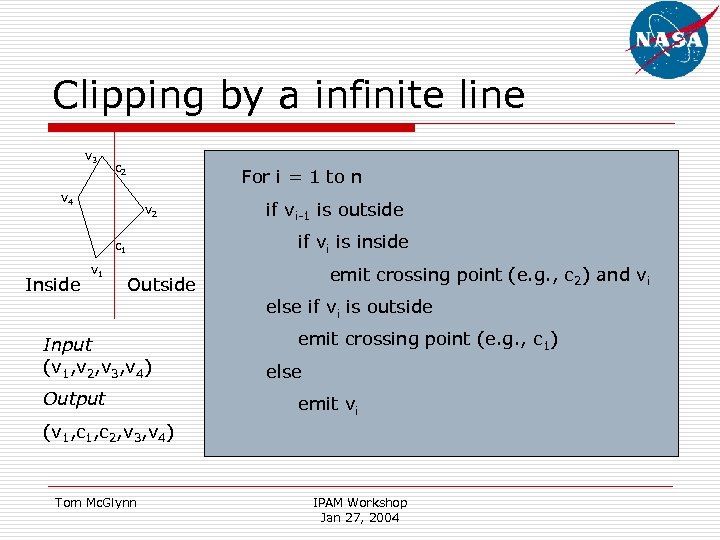Clipping by a infinite line v 3 c 2 For i = 1 to n v 4 v 2 if vi is inside c 1 Inside v 1 if vi-1 is outside Outside Input (v 1, v 2, v 3, v 4) Output emit crossing point (e. g. , c 2) and vi else if vi is outside emit crossing point (e. g. , c 1) else emit vi (v 1, c 2, v 3, v 4) Tom Mc. Glynn IPAM Workshop Jan 27, 2004

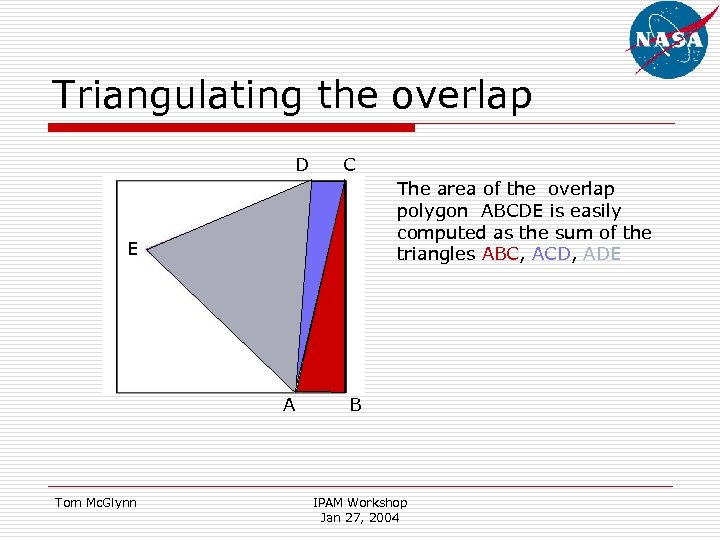Triangulating the overlap D C The area of the overlap polygon ABCDE is easily computed as the sum of the triangles ABC, ACD, ADE E A Tom Mc. Glynn B IPAM Workshop Jan 27, 2004

Normalization o Intensive images n n o Track total flux and overlapped area for each pixel and use ratio for pixel value. Preserves flat fielding Extensive images n n Just add flux. Preserves total flux Tom Mc. Glynn IPAM Workshop Jan 27, 2004

Features o o o Convexity of pixels allows simplification of algorithm (since convex regions clip convex regions to convex regions). Clipping on rectangular grid is especially easy but either grid could be triangular or hexagonal or even discontiguous. Don’t have to make clipping window the same as pixel boundaries. n n o o If clipping window is smaller we get Drizzle-like algorithm If clipping window is larger than pixels we have a variable box-car along with resampling. Easy to accommodate ‘bad’ pixels or regions. Symmetry between resampling and original grid n Can resample in the `convenient’ direction if transformation is easier one way or the other. Not the most ‘accurate’ algorithm, but it can be extremely robust. “Best worst-case resampler” Tom Mc. Glynn IPAM Workshop Jan 27, 2004

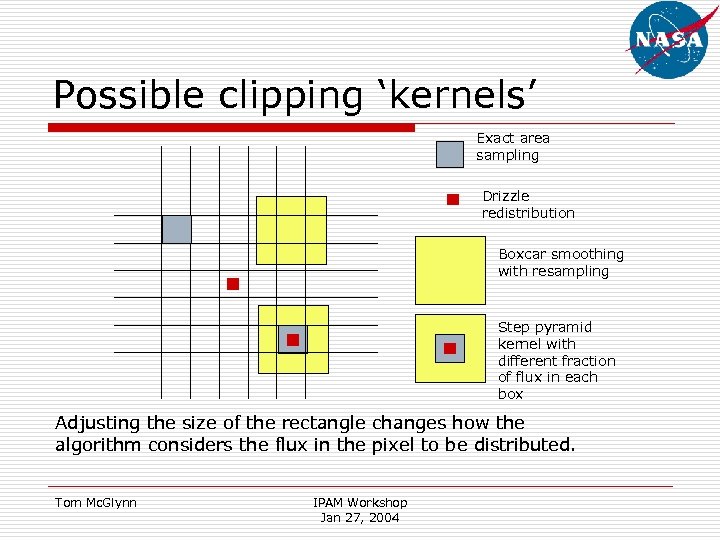Possible clipping ‘kernels’ Exact area sampling Drizzle redistribution Boxcar smoothing with resampling Step pyramid kernel with different fraction of flux in each box Adjusting the size of the rectangle changes how the algorithm considers the flux in the pixel to be distributed. Tom Mc. Glynn IPAM Workshop Jan 27, 2004

How can astronomers decide which resampling algorithm to use? o Accuracy n Does resampling affect astronomical measurements? o o Detection, Astrometry, Photometry, Morphology, Resolution Cost (CPU, memory) Complexity n Coding and comprehension costs Robustness n Point versus area resampling n How well does it work when in hard resampling situations? Tom Mc. Glynn IPAM Workshop Jan 27, 2004

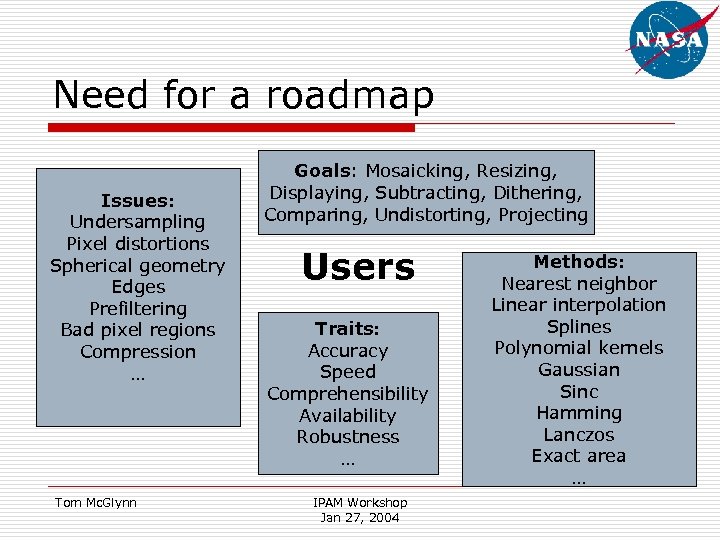Need for a roadmap Issues: Undersampling Pixel distortions Spherical geometry Edges Prefiltering Bad pixel regions Compression … Tom Mc. Glynn Goals: Mosaicking, Resizing, Displaying, Subtracting, Dithering, Comparing, Undistorting, Projecting Users Traits: Accuracy Speed Comprehensibility Availability Robustness … IPAM Workshop Jan 27, 2004 Methods: Nearest neighbor Linear interpolation Splines Polynomial kernels Gaussian Sinc Hamming Lanczos Exact area …

Analysis in other regimes Quantitative Comparison of Sinc. Approximating Kernels for Medical Image Interpolation Erik H. W. Meijering, Wiro J. Niessen, Josien P. W. Pluim, Max A. Viergever Round-robin resampling – a sequence of resamplings leading back to the original image. Good for determining the ‘best’, but not for assessing the cost • Truncated sinc resamplers are the worst. • Variety of higher order resamplers do pretty well. • But the images don’t look much like typical astronomical data) Tom Mc. Glynn IPAM Workshop Jan 27, 2004

… Image Reconstruction by Convolution with Symmetrical Piecewise nth-Order Polynomial Kernels Erik H. W. Meijering, Karel J. Zuiderveld, Max A. Viergever IEEE Transactions on Image Processing, vol. 8, no. 2, February 1999, pp. 192, 201. • Going beyond third order kernels doesn’t seem to buy one anything. Tom Mc. Glynn IPAM Workshop Jan 27, 2004

Comparing image resamplers via a model of the human vision system Richard Harvey, Stephen King, Richard Aldridge and J. Andrew Banghamh A big driver in commercial applications is rendering of text. Tom Mc. Glynn IPAM Workshop Jan 27, 2004

Even astronomical references often compare samplers in qualitative terms. Features in Lanczos resampling. NN LI Lcz 2 Lcz 3 Lcz 4 SWarp v 2: 0 User's guide E. Bertin Moire patterns in linearly interpolated resampled images Tom Mc. Glynn IPAM Workshop Jan 27, 2004

Measuring accuracy quantitatively o o Single resampling Astronomicalish images How does noise affect resampling? Two resampling scenarios: n n o o o Small Pixel: Rotation, final pixel size/original pixel size=1. 1 Big Pixel: Rotation, final pixel size/original pixel size=2. 5 Use Sextractor to estimate parameters of original and resampled objects. Model image with 100 gaussian objects and variable noise Use DSS image for reality check Tom Mc. Glynn IPAM Workshop Jan 27, 2004

Test Images 0: 0 (Number: Noise) 5: 0. 006 15: 0. 2 Tom Mc. Glynn 10: 0. 03 20: 1. 0 IPAM Workshop Jan 27, 2004

North Pole image DSS image Tom Mc. Glynn IPAM Workshop Jan 27, 2004

Samplers Tested o Interpolation algorithms n n o NN – Nearest Neighbor LI – Linear Interpolation LCZn – A Lanczos n-lobe interpolator (n=3, 4) SPn – An n’th order spline (n=3, 4) Redistribution algorithms n n n CL – Clipping exact area CL 0. 5 – Clipping using a window of half the size of the pixel (similar to Drizzle) MN –Montage exact area algorithm, resampling done on celestial sphere. Tom Mc. Glynn IPAM Workshop Jan 27, 2004

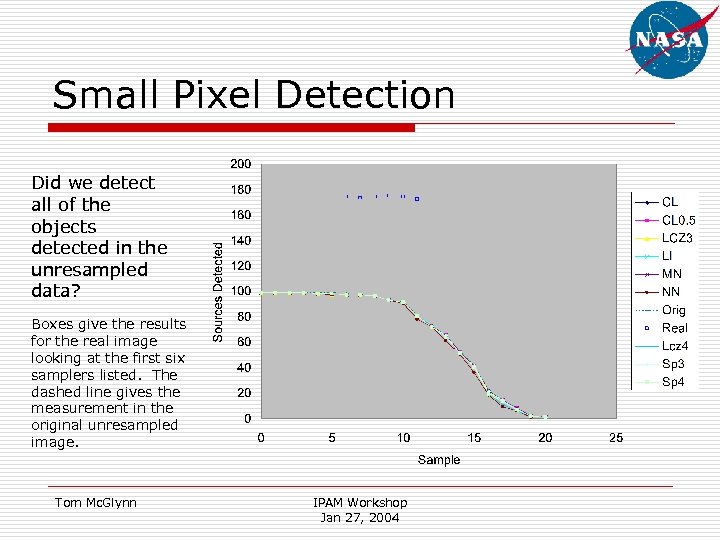Small Pixel Detection Did we detect all of the objects detected in the unresampled data? Boxes give the results for the real image looking at the first six samplers listed. The dashed line gives the measurement in the original unresampled image. Tom Mc. Glynn IPAM Workshop Jan 27, 2004

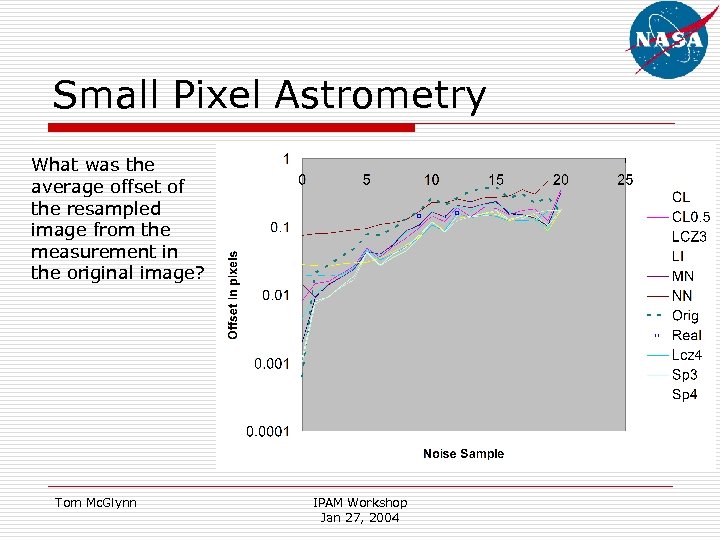Small Pixel Astrometry What was the average offset of the resampled image from the measurement in the original image? Tom Mc. Glynn IPAM Workshop Jan 27, 2004

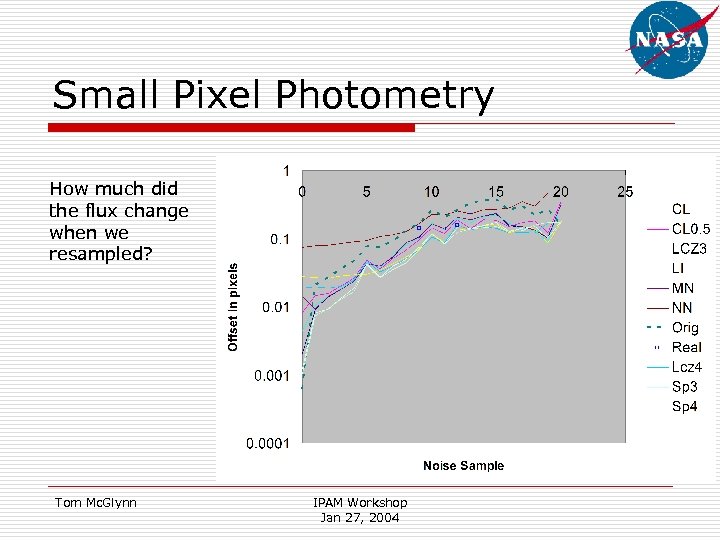Small Pixel Photometry How much did the flux change when we resampled? Tom Mc. Glynn IPAM Workshop Jan 27, 2004

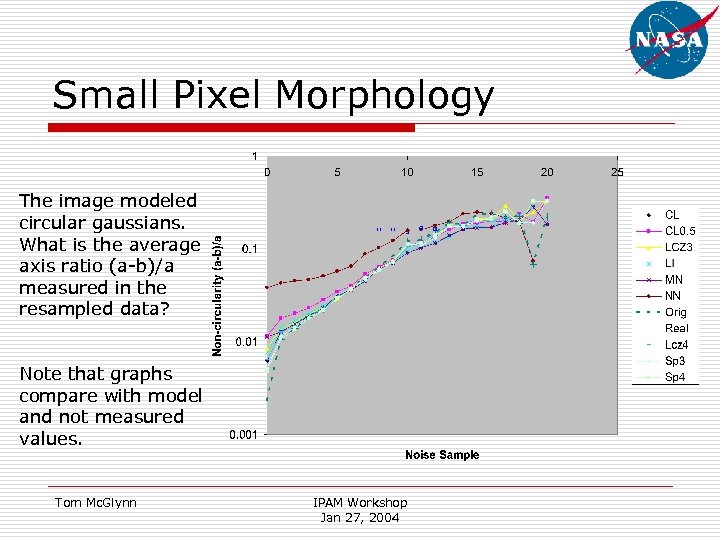Small Pixel Morphology The image modeled circular gaussians. What is the average axis ratio (a-b)/a measured in the resampled data? Note that graphs compare with model and not measured values. Tom Mc. Glynn IPAM Workshop Jan 27, 2004

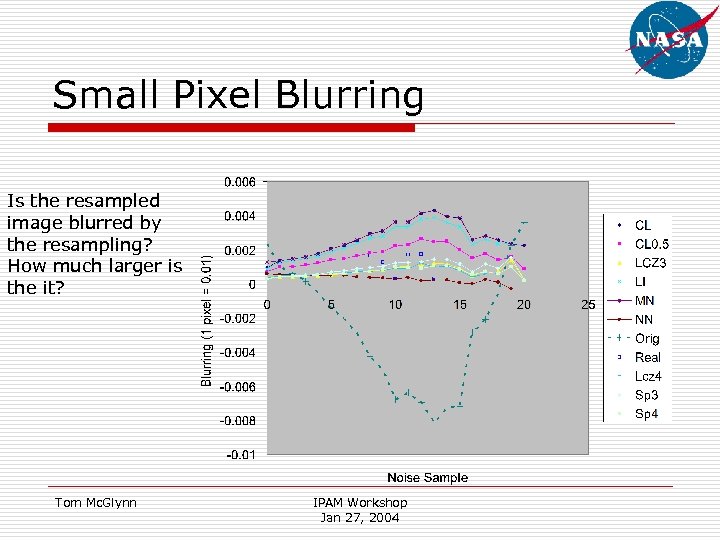Small Pixel Blurring Is the resampled image blurred by the resampling? How much larger is the it? Tom Mc. Glynn IPAM Workshop Jan 27, 2004

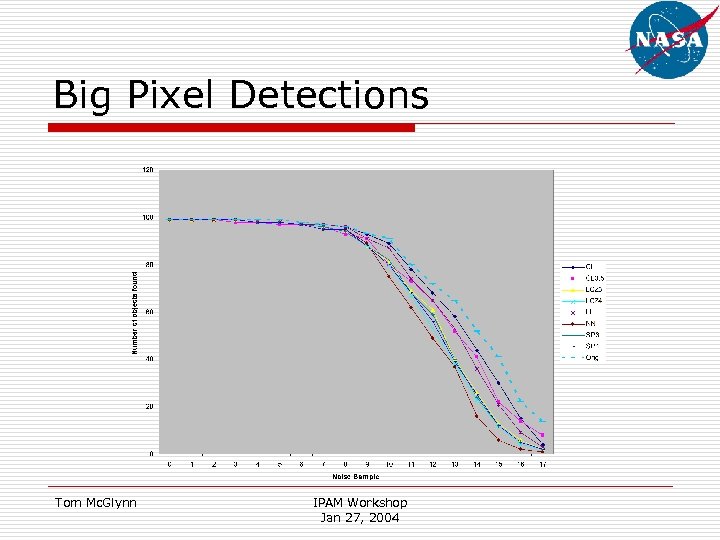Big Pixel Detections Tom Mc. Glynn IPAM Workshop Jan 27, 2004

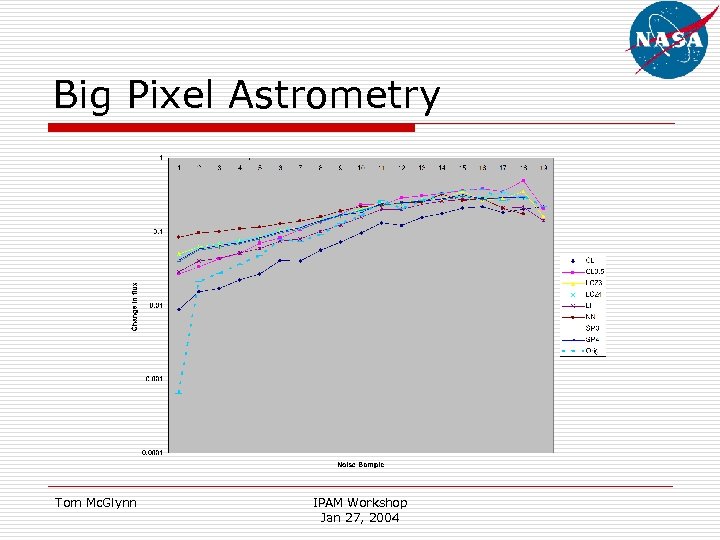Big Pixel Astrometry Tom Mc. Glynn IPAM Workshop Jan 27, 2004

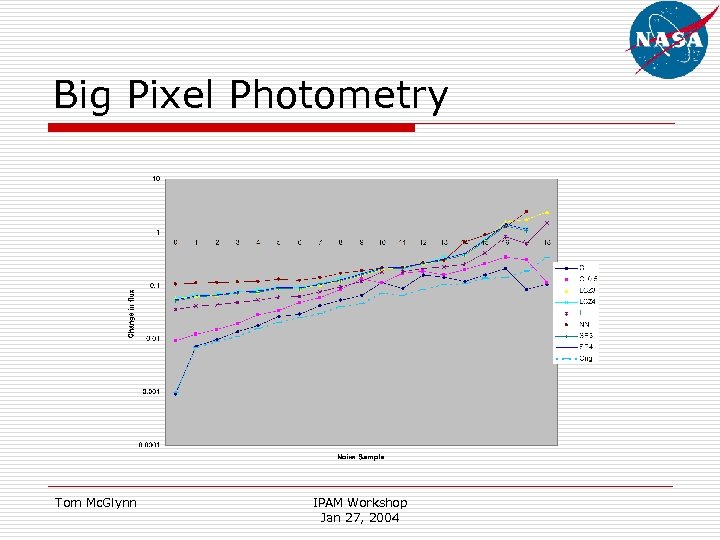Big Pixel Photometry Tom Mc. Glynn IPAM Workshop Jan 27, 2004

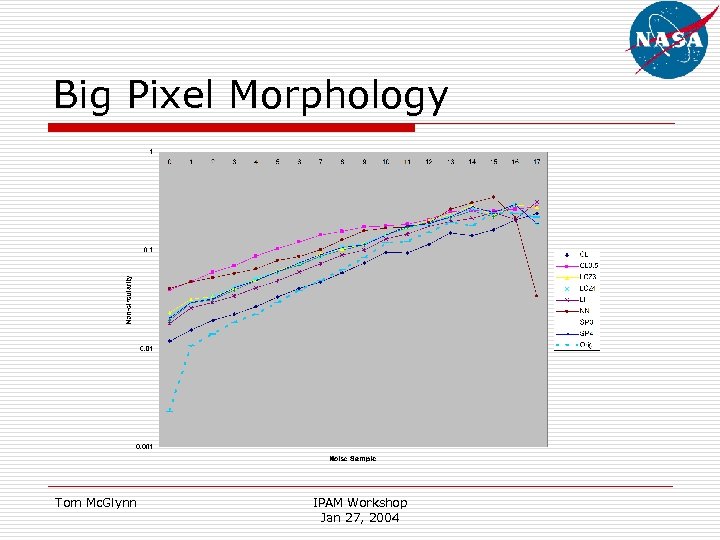Big Pixel Morphology Tom Mc. Glynn IPAM Workshop Jan 27, 2004

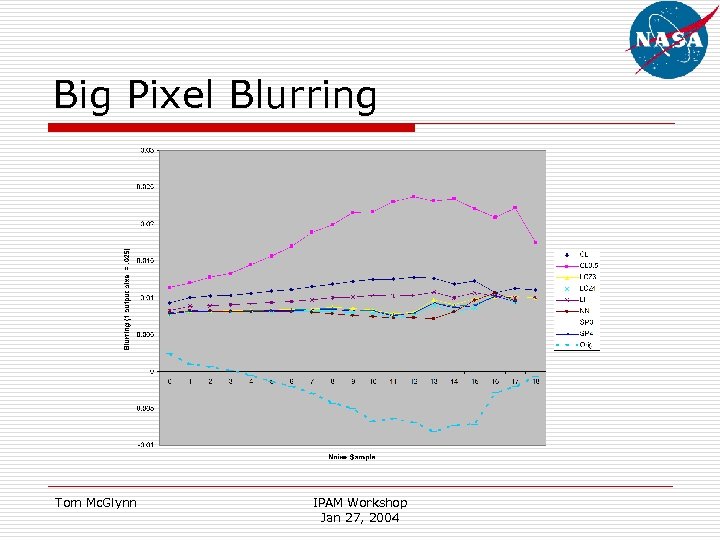Big Pixel Blurring Tom Mc. Glynn IPAM Workshop Jan 27, 2004

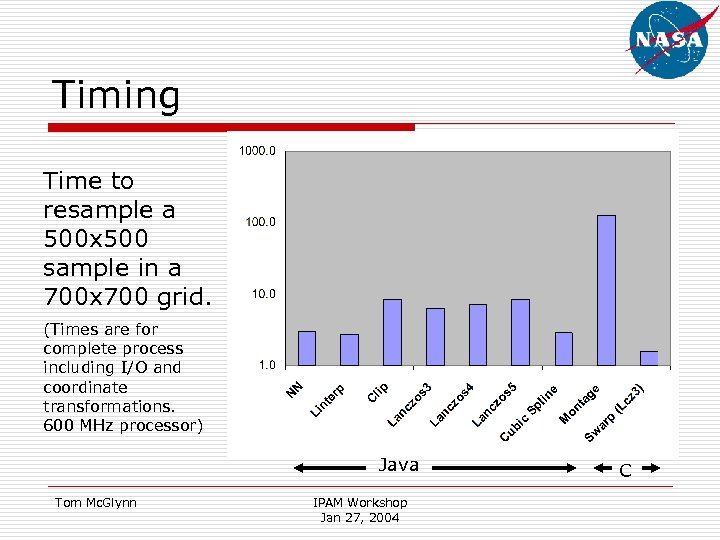Timing Time to resample a 500 x 500 sample in a 700 x 700 grid. (Times are for complete process including I/O and coordinate transformations. 600 MHz processor) Java Tom Mc. Glynn IPAM Workshop Jan 27, 2004 C

Complexity o o o Low order methods are trivial to program and relatively easy to test. Some higher order kernel interpolation methods are only modestly more complex. The initial computation of splines is more challenging, but splines are very easy to evaluate Previous exact area sampling techniques were complex and time prohibitive. Redistribution methods based on sample kernels can be comparable to interpolation methods. Clipping algorithm is relatively straightforward to understand but use a more algorithmic and less functional paradigm. Tom Mc. Glynn IPAM Workshop Jan 27, 2004

Robustness o Discontinuities, features, holes are harder to handle directly in higher order methods n o Prefiltering or image patching. Supersampling (averaging multiple sample points within a single resampling pixel) is an easy step towards area resampling for point resampling methods, but requires understanding how many samples should be made within each pixel. o Magnification of well-sampled images best done with high order samplers o High order samplers perform poorly on minified images and where pixel shapes are very different. Need a quantitative measurement of robustness. Tom Mc. Glynn IPAM Workshop Jan 27, 2004

Class 1 Resampling pixels are similar in most respects to input pixels: translations, small distortions and scale changes. • Use high order techniques, e. g. , Lanczos or spline methods when data is well sampled. The first is easier to program, the second is faster. Limited return from going beyond cubic spline or Lanczos 3. • Drizzle approach can limit blurring effects of redistribution while accommodating features or undersampling. • Noise induced errors typically outweigh sampling errors except for blurring. Tom Mc. Glynn IPAM Workshop Jan 27, 2004

Class 2 Resampling pixels substantially different from original pixels, but more or less constant over image. • For small resampling pixels (magnification) point sampling techniques should work with well behaved images. • When minifying, supersampling or inherently adaptive techniques, e. g. , exact area or other redistribution techniques are best. • Sampling errors can easily dominate errors due to noise. • Balance accuracy and robustness. Tom Mc. Glynn IPAM Workshop Jan 27, 2004

Class 3 Resampling pixels vary significantly over image. Big holes or features. Nonrectangular, non-contiguous grids? • Use adaptive resampling techniques. Exact area sampling is a good bet. • Use best robust techniques. • Objects are going to have substantial distortions in original or sampled grid. Tom Mc. Glynn IPAM Workshop Jan 27, 2004

Concluding thoughts o No single best resampling technique. n n o Too empirical n n o Probably a small suite algorithms can serve for a wide variety of situations. Can algorithms self-select? Can robustness be defined quantitatively? Can we predict accuracy of resamplers? Lots more to consider: n n Extended objects What is the interplay of resampling with other elements of processing, e. g. , compresion? Tom Mc. Glynn IPAM Workshop Jan 27, 2004