Practice You bought a ticket for a

Practice • You bought a ticket for a fire department lottery and your brother has bought two tickets. You just read that 1000 tickets were sold. – a) What is the probability you will win the grand prize? – b) What is the probability that your brother will win? – c) What is the probably that you or your bother will win?

5. 2 • A) 1/1000 =. 001 • B)2/1000 =. 002 • C). 001 +. 002 =. 003

Practice • Assume the same situation at before except only a total of 10 tickets were sold and there are two prizes. – a) Given that you didn’t win the first prize, what is the probability you will win the second prize? – b) What is the probability that your borther will win the first prize and you will win the second prize? – c) What is the probability that you will win the first prize and your brother will win the second prize? – d) What is the probability that the two of you will win the first and second prizes?

5. 3 • • A) 1/9 =. 111 B) 2/10 * 1/9 = (. 20)*(. 111) =. 022 C) 1/10 * 2/9 = (. 10)*(. 22) =. 022 D). 022 +. 022 =. 044

Practice • In some homes a mother’s behavior seems to be independent of her baby's, and vice versa. If the mother looks at her child a total of 2 hours each day, and the baby looks at the mother a total of 3 hours each day, and if they really do behave independently, what is the probability that they will look at each other at the same time?

5. 8 • 2/24 =. 083 • 3/24 =. 125 • . 083*. 125 =. 01

Practice • Abe ice-cream shot has six different flavors of ice cream, and you can order any combination of any number of them (but only one scoop of each flavor). How many different ice-cream cone combinations could they truthfully advertise (note, we don’t care about the order of the scoops and an empty cone doesn’t count).

5. 29 6 + 15 + 20 +15 + 6 + 1 = 63

• Suppose you live in a place that has a constant chance of being struck by lightning at any time through the year. Suppose that the strikes are random: every day the chance of a strike is the same, and the rate works out to one strike a month. Your house is hit by lightning today, Monday. What is the most likely day for the next bolt to strike your house?

• Tuesday! • Say the prob of lighting hitting is. 025 • On Tues prob of hitting is. 025 • For Wed to be next hit this would have to be true: no hit on Tues AND hit on Wed 975*. 025=. 0243 • For Thursday. 975*. 025=. 0237

Remember • Playing perfect black jack – the probability of winning a hand is. 498 • What is the probability that you will win 8 of the next 10 games of blackjack?

Binomial Distribution Ingredients: N = total number of events p = the probability of a success on any one trial q = (1 – p) = the probability of a failure on any one trial X = number of successful events

Binomial Distribution p =. 0429 Ingredients: N = total number of events p = the probability of a success on any one trial q = (1 – p) = the probability of a failure on any one trial X = number of successful events

Binomial Distribution • What if you are interested in the probability of winning at least 8 games of black jack? • To do this you need to know the distribution of these probabilities

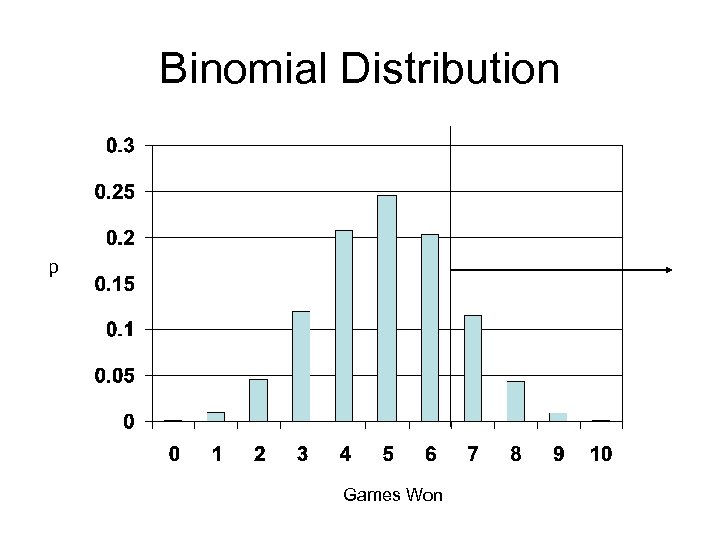
Probability of Winning Blackjack Number of Wins • p =. 498, N = 10 0 1 2 3 4 5 6 7 8 9 10 p

Probability of Winning Blackjack Number of Wins • p =. 498, N = 10 p 0 . 001 1 2 3 4 5 6 7 8 9 10

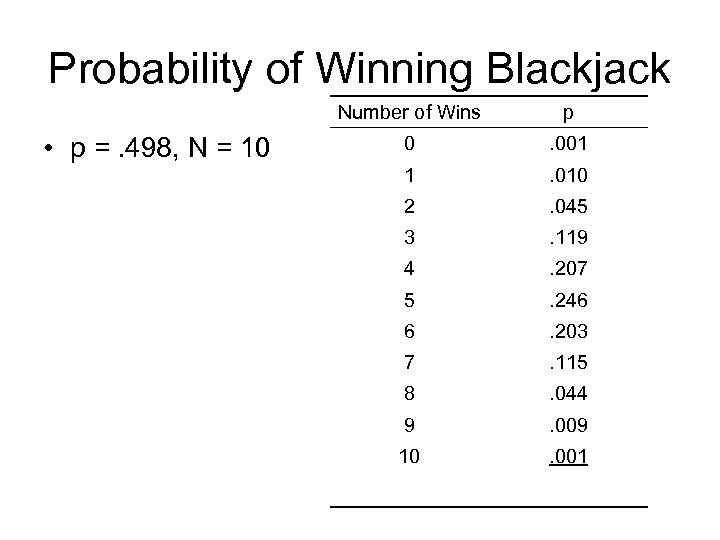
Probability of Winning Blackjack Number of Wins • p =. 498, N = 10 p 0 . 001 1 . 010 2 . 045 3 . 119 4 . 207 5 . 246 6 . 203 7 . 115 8 . 044 9 . 009 10 . 001

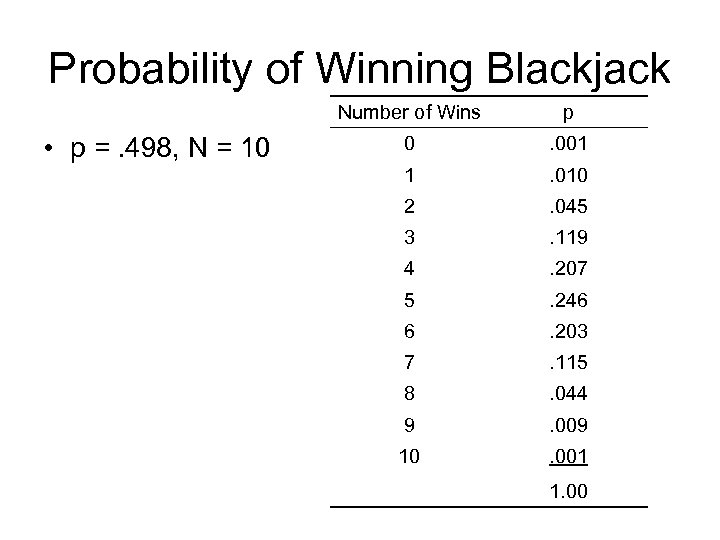
Probability of Winning Blackjack Number of Wins • p =. 498, N = 10 p 0 . 001 1 . 010 2 . 045 3 . 119 4 . 207 5 . 246 6 . 203 7 . 115 8 . 044 9 . 009 10 . 001 1. 00

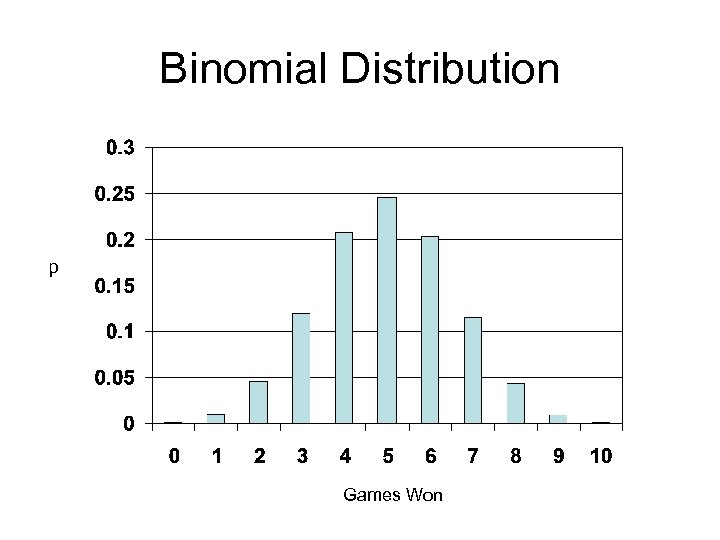
Binomial Distribution p Games Won

Hypothesis Testing • You wonder if winning at least 7 games of blackjack is significantly (. 05) better than what would be expected due to chance. • H 1= Games won > 6 • H 0= Games won < or equal to 6 • What is the probability of winning 7 or more games?

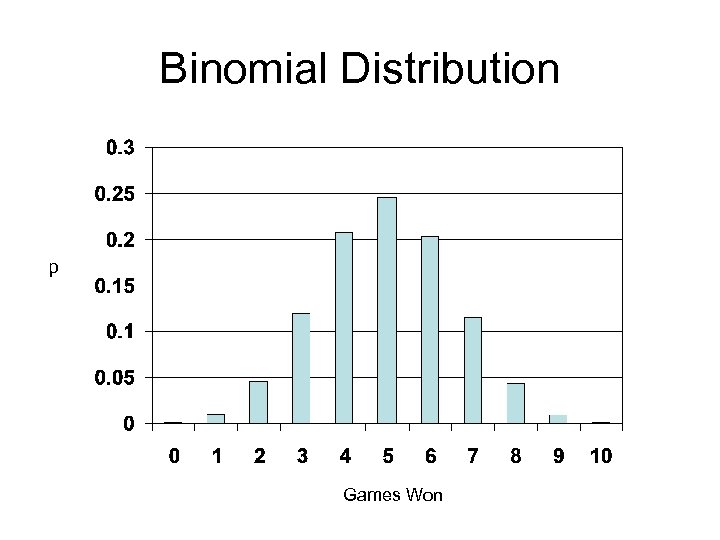
Binomial Distribution p Games Won

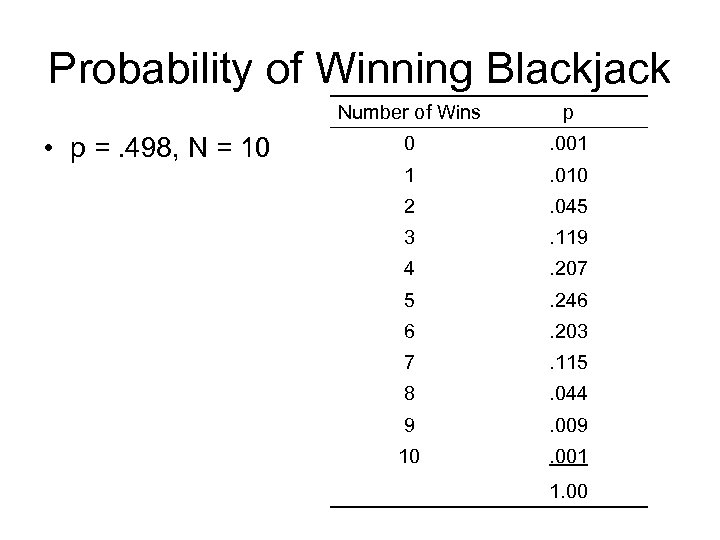
Probability of Winning Blackjack Number of Wins • p =. 498, N = 10 p 0 . 001 1 . 010 2 . 045 3 . 119 4 . 207 5 . 246 6 . 203 7 . 115 8 . 044 9 . 009 10 . 001 1. 00

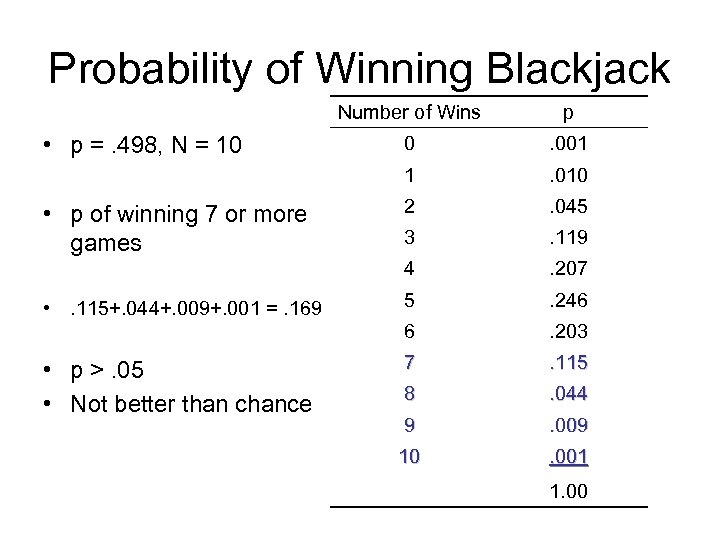
Probability of Winning Blackjack Number of Wins • p >. 05 • Not better than chance . 010 2 . 045 3 . 119. 207 5 . 246 6 • . 115+. 044+. 009+. 001 =. 169 . 001 4 • p of winning 7 or more games 0 1 • p =. 498, N = 10 p . 203 7 . 115 8 . 044 9 . 009 10 . 001 1. 00

Practice • The probability at winning the “Statistical Slot Machine” is. 08. • Create a distribution of probabilities when N = 10 • Determine if winning at least 4 games of slots is significantly (. 05) better than what would be expected due to chance.

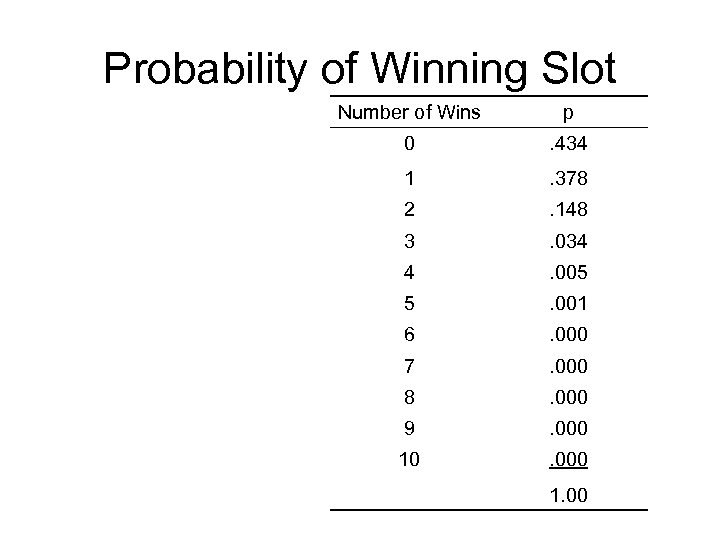
Probability of Winning Slot Number of Wins p 0 . 434 1 . 378 2 . 148 3 . 034 4 . 005 5 . 001 6 . 000 7 . 000 8 . 000 9 . 000 10 . 000 1. 00

Binomial Distribution p Games Won

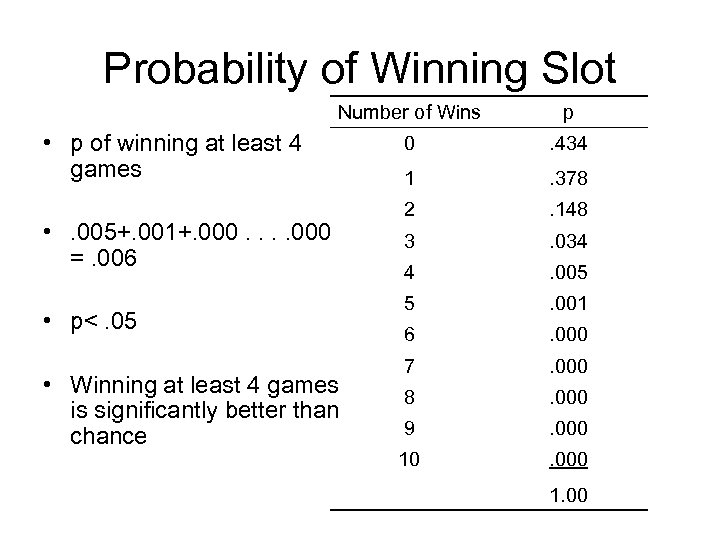
Probability of Winning Slot Number of Wins p 0 . 434 1 . 378 2 . 148 3 . 034 4 . 005 5 . 001 6 . 000 7 . 000 8 . 000 9 . 000 10 . 000 • p of winning at least 4 games • . 005+. 001+. 000 =. 006 • p<. 05 • Winning at least 4 games is significantly better than chance 1. 00

Binomial Distribution • These distributions can be described with means and SD. • Mean = Np • SD =

Binomial Distribution • Black Jack; p =. 498, N =10 • M = 4. 98 • SD = 1. 59

Binomial Distribution p Games Won

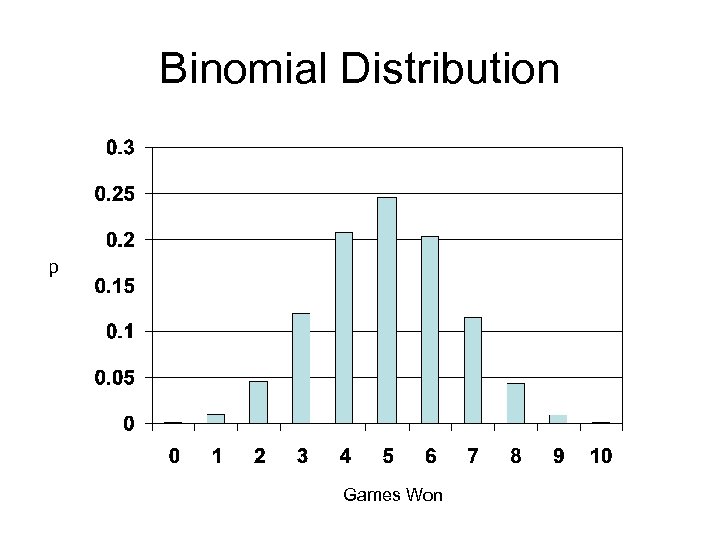
Binomial Distribution • Statistical Slot Machine; p =. 08, N = 10 • M =. 8 • SD =. 86

Binomial Distribution Note: as N gets bigger, distributions will approach normal p Games Won

Next Step • You think someone is cheating at BLINGOO! • p =. 30 of winning • You watch a person play 89 games of blingoo and wins 39 times (i. e. , 44%). • Is this significantly bigger than. 30 to assume that he is cheating?

Hypothesis • H 1=. 44 >. 30 • H 0=. 44 < or equal to. 30 • Or • H 1= 39 wins > 26. 7 wins • H 0= 39 wins < or equal to 26. 7 wins

Distribution • Mean = 26. 7 • SD = 4. 32 • X = 39

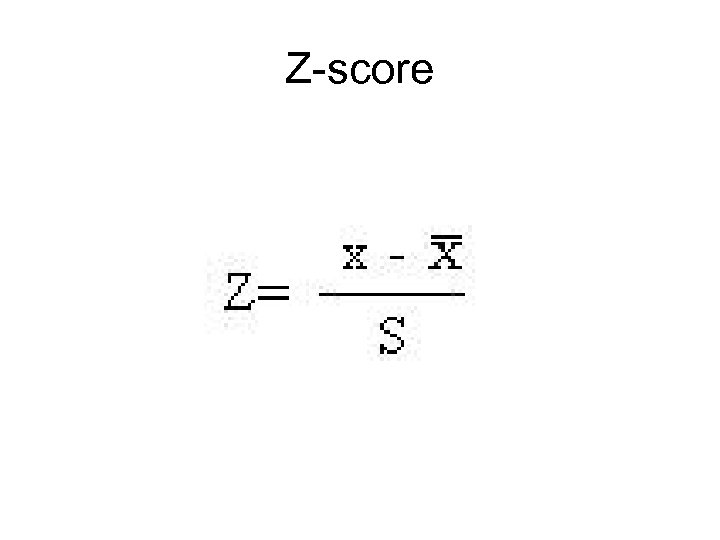
Z-score

Results • (39 – 26. 7) / 4. 32 = 2. 85 • p =. 0021 • p <. 05 • . 44 is significantly bigger than. 30. There is reason to believe the person is cheating! • Or – 39 wins is significantly more than 26. 7 wins (which are what is expected due to chance)

BLINGOO Competition • You and your friend enter at competition with 2, 642 other players • p =. 30 • You win 57 of the 150 games and your friend won 39. • Afterward you wonder how many people – A) did better than you? – B) did worse than you? – C) won between 39 and 57 games • You also wonder how many games you needed to win in order to be in the top 10%

Blingoo • M = 45 • SD = 5. 61 • A) did better than you? • (57 – 45) / 5. 61 = 2. 14 • p =. 0162 • 2, 642 *. 0162 = 42. 8 or 43 people

Blingoo • M = 45 • SD = 5. 61 • A) did worse than you? • (57 – 45) / 5. 61 = 2. 14 • p =. 9838 • 2, 642 *. 9838 = 2, 599. 2 or 2, 599 people

Blingoo • M = 45 • SD = 5. 61 • A) won between 39 and 57 games? • • (57 – 45) / 5. 61 = 2. 14 ; p =. 4838 (39 – 45) / 5. 61 = -1. 07 ; p =. 3577 . 4838 +. 3577 =. 8415 2, 642 *. 8415 = 2, 223. 2 or 2, 223 people

Blingoo • M = 45 • SD = 5. 61 • You also wonder how many games you needed to win in order to be in the top 10% • Z = 1. 28 • 45 + 5. 61 (1. 28) = 52. 18 games or 52 games

Is a persons’ size related to if they were bullied • You gathered data from 209 children at Springfield Elementary School. • Assessed: • Height (short vs. not short) • Bullied (yes vs. no)

Results Ever Bullied

Is this difference in proportion due to chance? • To test this you use a Chi-Square ( 2) • Notice you are using nominal data

Hypothesis • H 1: There is a relationship between the two variables – i. e. , a persons size is related to if they were bullied • H 0: The two variables are independent of each other – i. e. , there is no relationship between a persons size and if they were bullied

Logic • 1) Calculate an observed Chi-square • 2) Find a critical value • 3) See if the observed Chi-square falls in the critical area

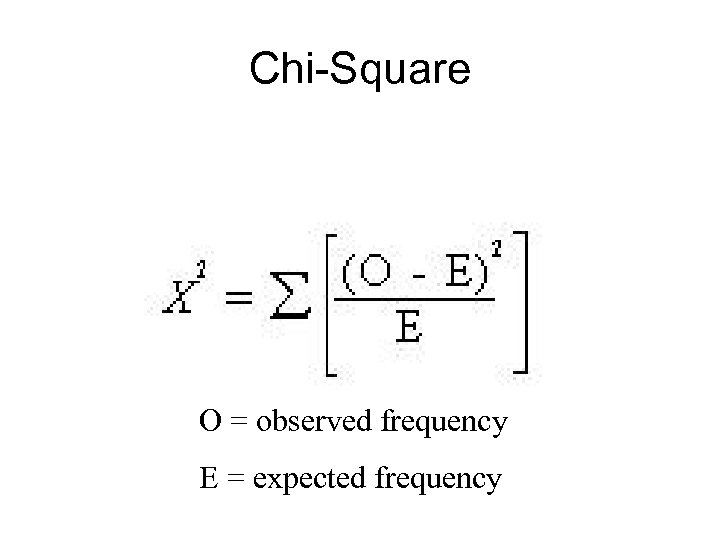
Chi-Square O = observed frequency E = expected frequency

Results Ever Bullied

Observed Frequencies Ever Bullied

Expected frequencies • Are how many observations you would expect in each cell if the null hypothesis was true – i. e. , there was no relationship between a persons size and if they were bullied

Expected frequencies • To calculate a cells expected frequency: • For each cell you do this formula

Expected Frequencies Ever Bullied

Expected Frequencies Row total = 92 Ever Bullied

Expected Frequencies Row total = 92 Column total = 72 Ever Bullied

Expected Frequencies Row total = 92 N = 209 Column total = 72 Ever Bullied

Expected Frequencies E = (92 * 72) /209 = 31. 69 Ever Bullied

Expected Frequencies Ever Bullied

Expected Frequencies E = (92 * 137) /209 = 60. 30 Ever Bullied

Expected Frequencies E = (117 * 72) / 209 = 40. 30 E = (117 * 137) / 209 = 76. 69 Ever Bullied

Expected Frequencies The expected frequencies are what you would expect if there was no relationship between the two variables! Ever Bullied

How do the expected frequencies work? Looking only at: Ever Bullied

How do the expected frequencies work? If you randomly selected a person from these 209 people what is the probability you would select a person who is short? Ever Bullied

How do the expected frequencies work? If you randomly selected a person from these 209 people what is the probability you would select a person who is short? 92 / 209 =. 44 Ever Bullied

How do the expected frequencies work? If you randomly selected a person from these 209 people what is the probability you would select a person who was bullied? Ever Bullied

How do the expected frequencies work? If you randomly selected a person from these 209 people what is the probability you would select a person who was bullied? 72 / 209 =. 34 Ever Bullied

How do the expected frequencies work? If you randomly selected a person from these 209 people what is the probability you would select a person who was bullied and is short? Ever Bullied

How do the expected frequencies work? If you randomly selected a person from these 209 people what is the probability you would select a person who was bullied and is short? (. 44) (. 34) =. 15 Ever Bullied

How do the expected frequencies work? How many people do you expect to have been bullied and short? Ever Bullied

How do the expected frequencies work? How many people would you expect to have been bullied and short? (. 15 * 209) = 31. 35 (difference due to rounding) Ever Bullied

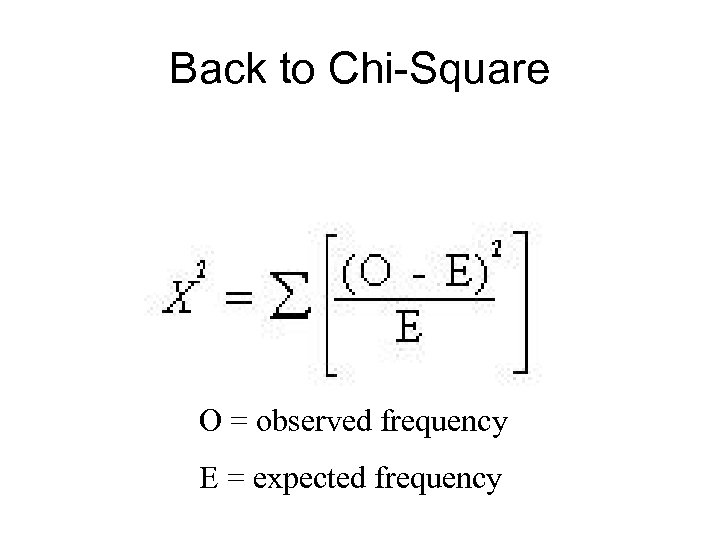
Back to Chi-Square O = observed frequency E = expected frequency

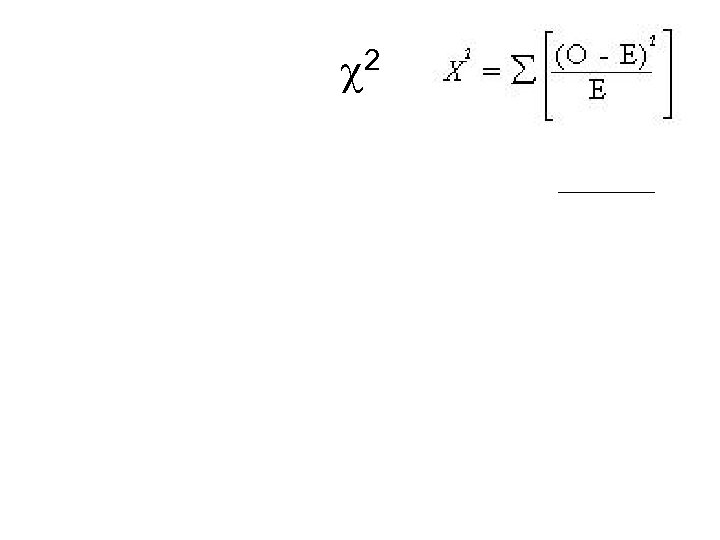
2

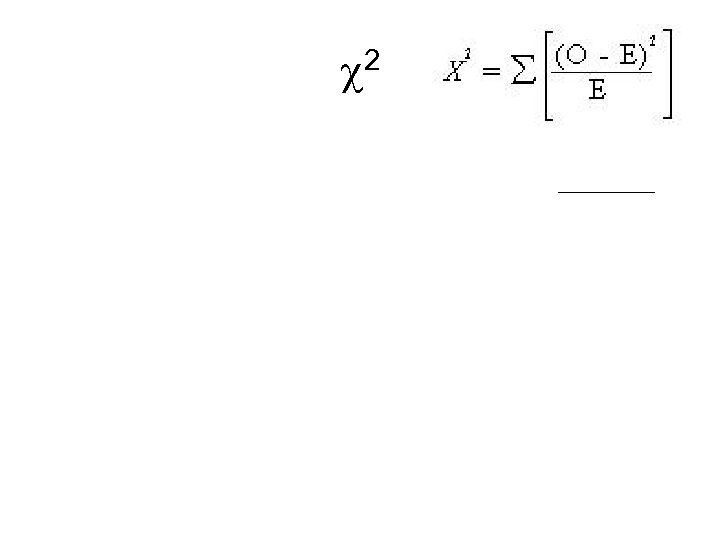
2

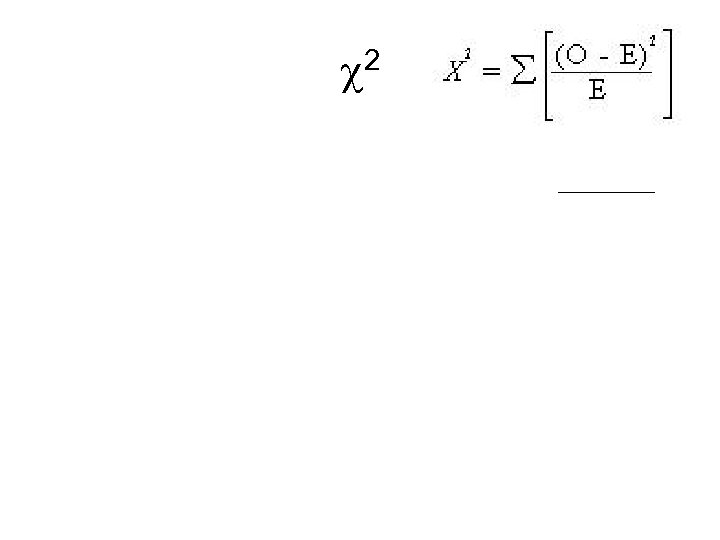
2

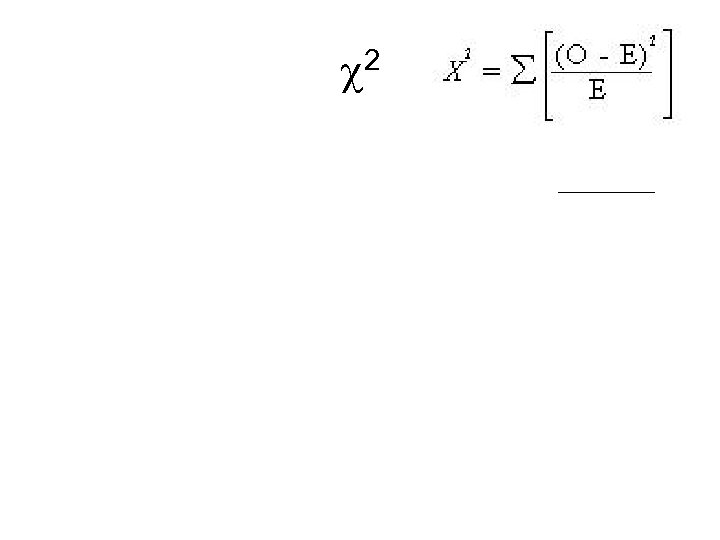
2

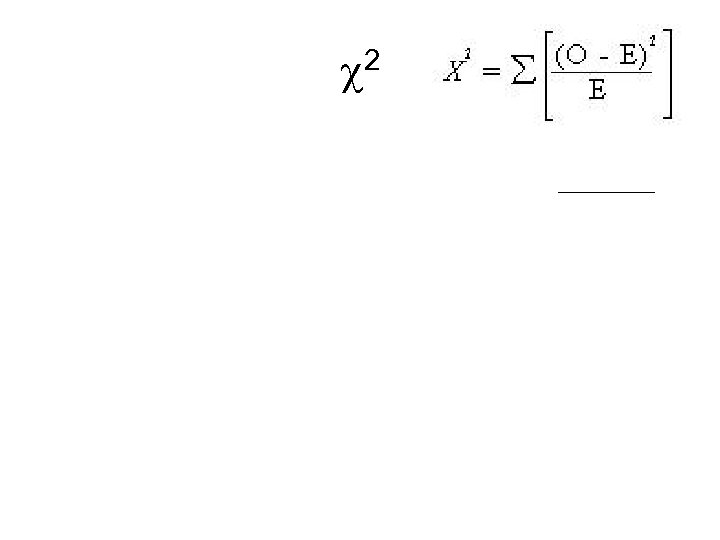
2

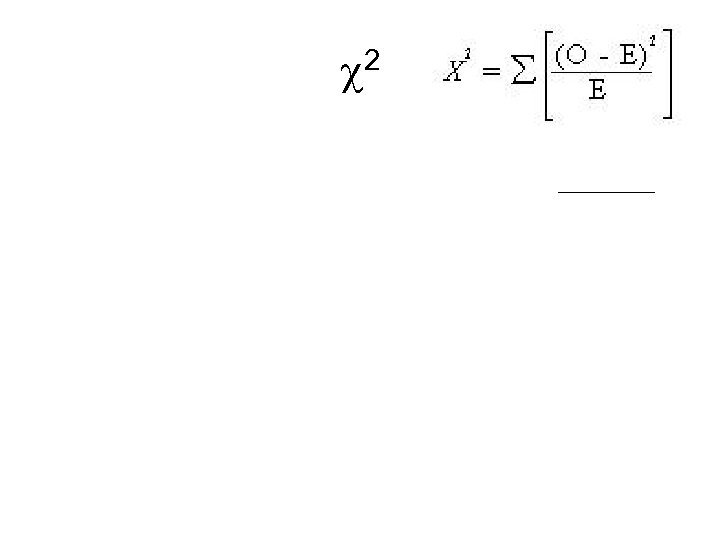
2

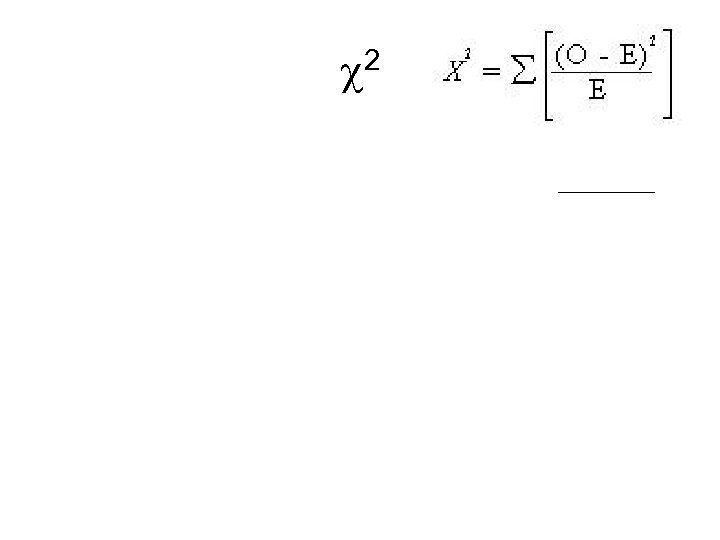
2

Significance • Is a 2 of 9. 13 significant at the. 05 level? • To find out you need to know df

Degrees of Freedom • To determine the degrees of freedom you use the number of rows (R) and the number of columns (C) • DF = (R - 1)(C - 1)

Degrees of Freedom Rows = 2 Ever Bullied

Degrees of Freedom Rows = 2 Columns = 2 Ever Bullied

Degrees of Freedom • To determine the degrees of freedom you use the number of rows (R) and the number of columns (C) • df = (R - 1)(C - 1) • df = (2 - 1) = 1

Significance • Look on page 736 • df = 1 • =. 05 • 2 critical = 3. 84

Decision • Thus, if 2 > than 2 critical – Reject H 0, and accept H 1 • If 2 < or = to 2 critical – Fail to reject H 0

Current Example • 2 = 9. 13 • 2 critical = 3. 84 • Thus, reject H 0, and accept H 1

Current Example • H 1: There is a relationship between the two variables – A persons size is significantly (alpha =. 05) related to if they were bullied