lecture_4.pptx
- Количество слайдов: 43
 Practical Data Mining Lecture 4. Supervised learning (part 3) + unsupervised learning (part 2). Victor Kantor MIPT 2014
Practical Data Mining Lecture 4. Supervised learning (part 3) + unsupervised learning (part 2). Victor Kantor MIPT 2014
 Plan 1. 2. 3. 4. 5. 6. Linear classification Semi-supervised learning Linear regression Decision trees Ensemble methods Bonus-track
Plan 1. 2. 3. 4. 5. 6. Linear classification Semi-supervised learning Linear regression Decision trees Ensemble methods Bonus-track
 Plan 1. 2. 3. 4. 5. 6. Linear classification Semi-supervised learning Linear regression Decision trees Ensemble methods Bonus-track unsupervised learning
Plan 1. 2. 3. 4. 5. 6. Linear classification Semi-supervised learning Linear regression Decision trees Ensemble methods Bonus-track unsupervised learning
 Linear classification • • • Idea of linear classification Loss functions Gradient decent Stochastic gradient decent Regularization Standard linear classifiers
Linear classification • • • Idea of linear classification Loss functions Gradient decent Stochastic gradient decent Regularization Standard linear classifiers
 Idea of linear classification Geometric interpretation: separating hyperplane
Idea of linear classification Geometric interpretation: separating hyperplane
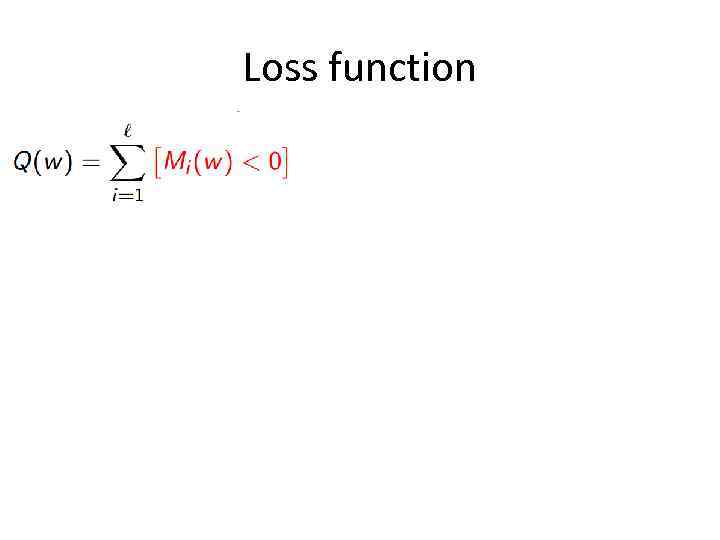 Loss function
Loss function
 Loss function Empirical risk function Loss function
Loss function Empirical risk function Loss function
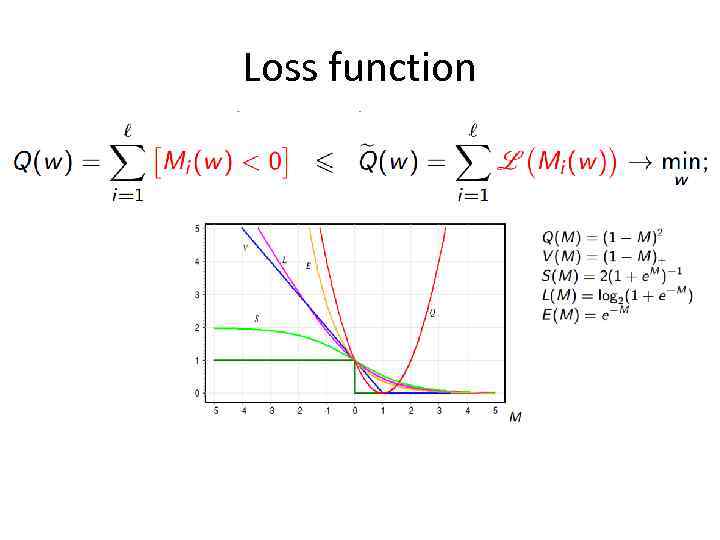 Loss function
Loss function
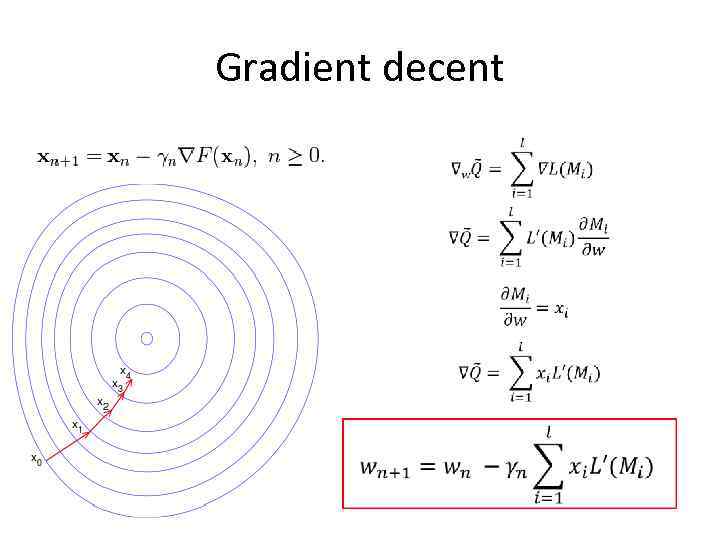 Gradient decent
Gradient decent
 Stochastic gradient decent
Stochastic gradient decent
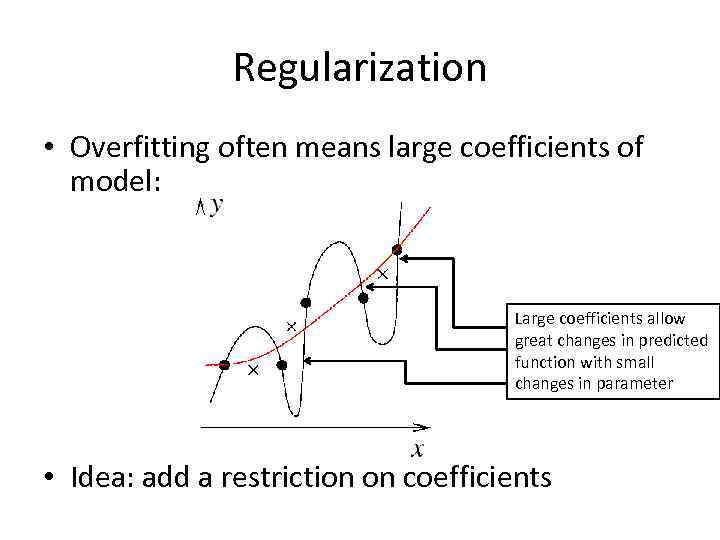 Regularization • Overfitting often means large coefficients of model: Large coefficients allow great changes in predicted function with small changes in parameter • Idea: add a restriction on coefficients
Regularization • Overfitting often means large coefficients of model: Large coefficients allow great changes in predicted function with small changes in parameter • Idea: add a restriction on coefficients
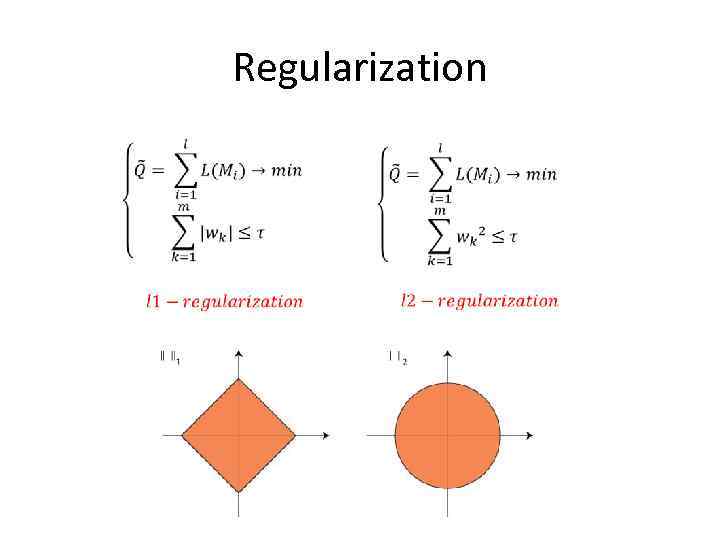 Regularization
Regularization
 Regularization
Regularization
 Differences between l 1 and l 2 • Sparseness – l 1 makes weight vector more sparse (having more zero values) • In linear classification case what means feature selection: features with zero weights are not used in classification • Simple geometric explanation of sparseness:
Differences between l 1 and l 2 • Sparseness – l 1 makes weight vector more sparse (having more zero values) • In linear classification case what means feature selection: features with zero weights are not used in classification • Simple geometric explanation of sparseness:
 Standard linear classifiers Classifier SVM (Support vector machine) Logistic regression LDA (Linear Discriminant Analysis or Linear Fisher’s Discriminant) Loss function Regularizer
Standard linear classifiers Classifier SVM (Support vector machine) Logistic regression LDA (Linear Discriminant Analysis or Linear Fisher’s Discriminant) Loss function Regularizer
 Semi-supervised learning • Motivation • Semi-supervised SVM • Entropy regularizer
Semi-supervised learning • Motivation • Semi-supervised SVM • Entropy regularizer
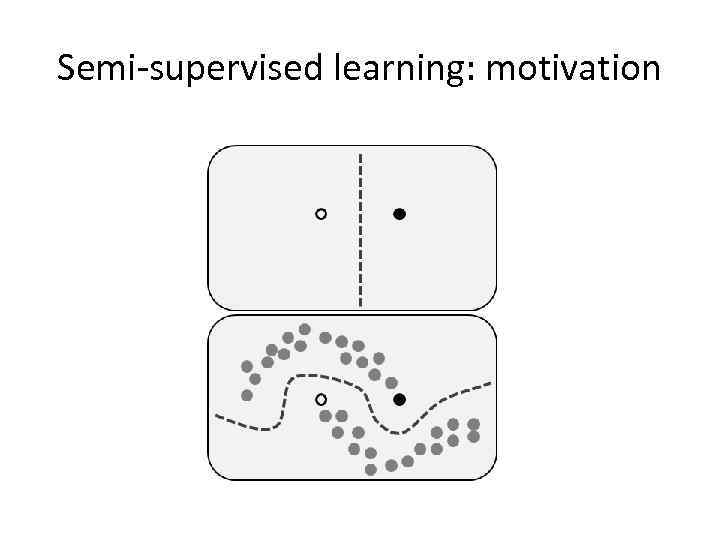 Semi-supervised learning: motivation
Semi-supervised learning: motivation
 Semi-supervised SVM (S 3 VM) SVM: Idea:
Semi-supervised SVM (S 3 VM) SVM: Idea:
 Semi-supervised logistic regression (entropy regularizer)
Semi-supervised logistic regression (entropy regularizer)
 Linear regression • • Model and matrix formulation Analytic derivation Geometric interpretation Regularization: LASSO and ridge regression
Linear regression • • Model and matrix formulation Analytic derivation Geometric interpretation Regularization: LASSO and ridge regression
 Model and matrix formulation •
Model and matrix formulation •
 Model and matrix formulation
Model and matrix formulation
 Analytic derivation
Analytic derivation
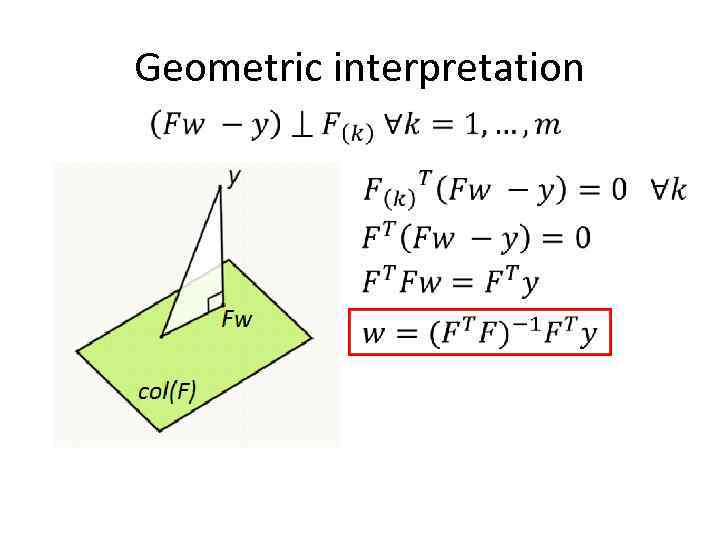 Geometric interpretation
Geometric interpretation
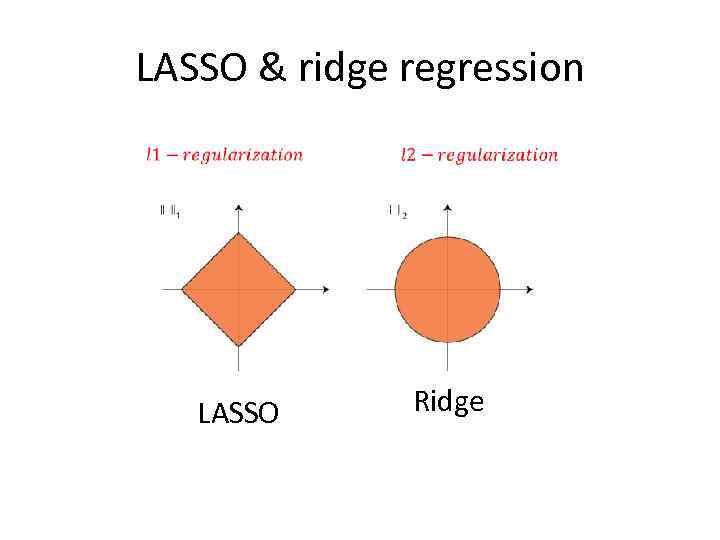 LASSO & ridge regression LASSO Ridge
LASSO & ridge regression LASSO Ridge
 Decision Trees • • • How decision tree works Criteria: exact Ficher’s test, Information Gain Greedy algorithm: ID 3 The idea of regression trees Additional topics
Decision Trees • • • How decision tree works Criteria: exact Ficher’s test, Information Gain Greedy algorithm: ID 3 The idea of regression trees Additional topics
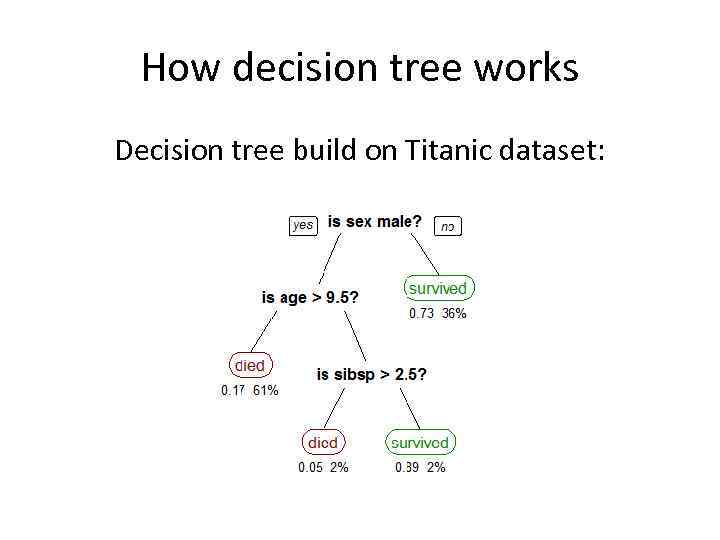 How decision tree works Decision tree build on Titanic dataset:
How decision tree works Decision tree build on Titanic dataset:
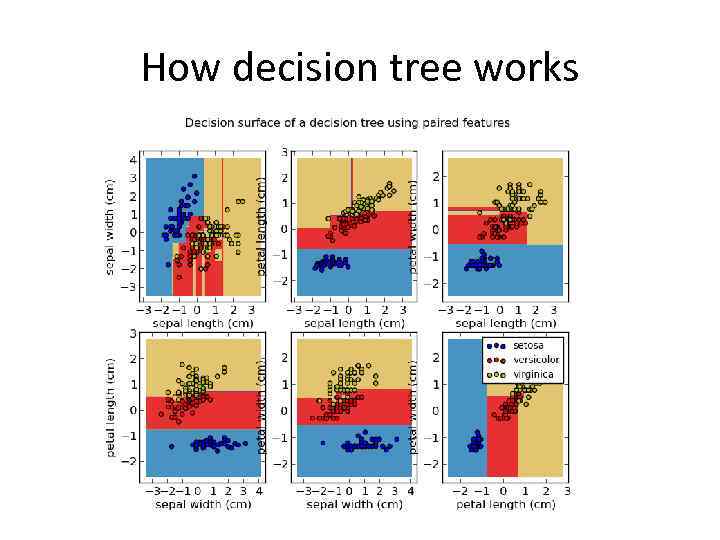 How decision tree works
How decision tree works
 Exact Fisher’s test & information gain
Exact Fisher’s test & information gain
 ID 3 •
ID 3 •
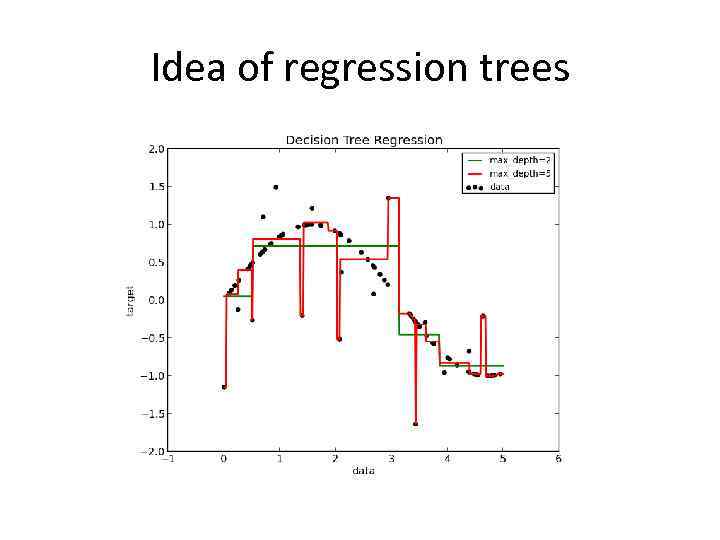 Idea of regression trees
Idea of regression trees
 Additional topics • • • C 4. 5 CART Post-pruning Pre-pruning Features binarization
Additional topics • • • C 4. 5 CART Post-pruning Pre-pruning Features binarization
 Ensemble methods • Standard ensemble construction methods • Random Forest • Gradient Boosting Machines, Gradient Tree Boosting
Ensemble methods • Standard ensemble construction methods • Random Forest • Gradient Boosting Machines, Gradient Tree Boosting
 Standard ensemble construction methods • • • Bagging Random subspace method (RSM) Blending Stacking Boosting
Standard ensemble construction methods • • • Bagging Random subspace method (RSM) Blending Stacking Boosting
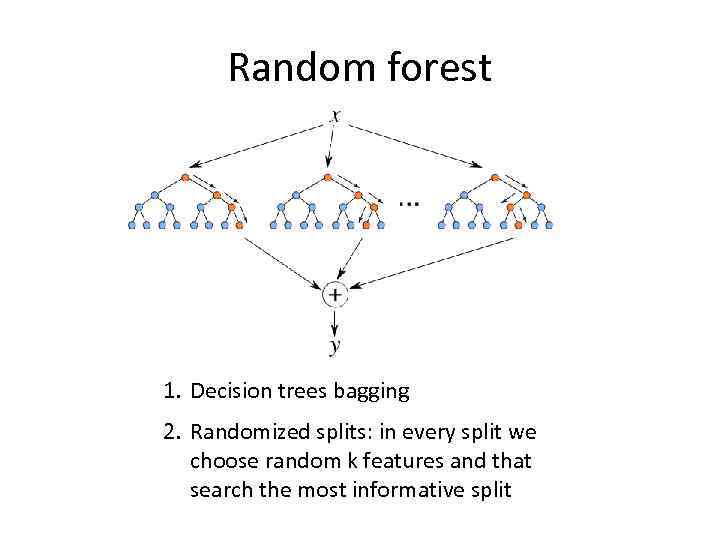 Random forest 1. Decision trees bagging 2. Randomized splits: in every split we choose random k features and that search the most informative split
Random forest 1. Decision trees bagging 2. Randomized splits: in every split we choose random k features and that search the most informative split
 Gradient boosting
Gradient boosting
 Gradient boosting
Gradient boosting
 Bonus-track: SVD example for previous lecture
Bonus-track: SVD example for previous lecture
 Bonus-track: SVD example for previous lecture
Bonus-track: SVD example for previous lecture
 Bonus-track: SVD example for previous lecture
Bonus-track: SVD example for previous lecture
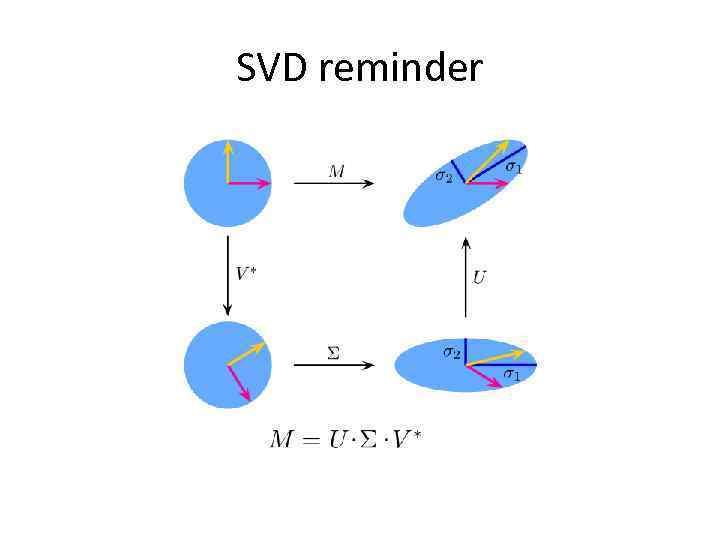 SVD reminder
SVD reminder
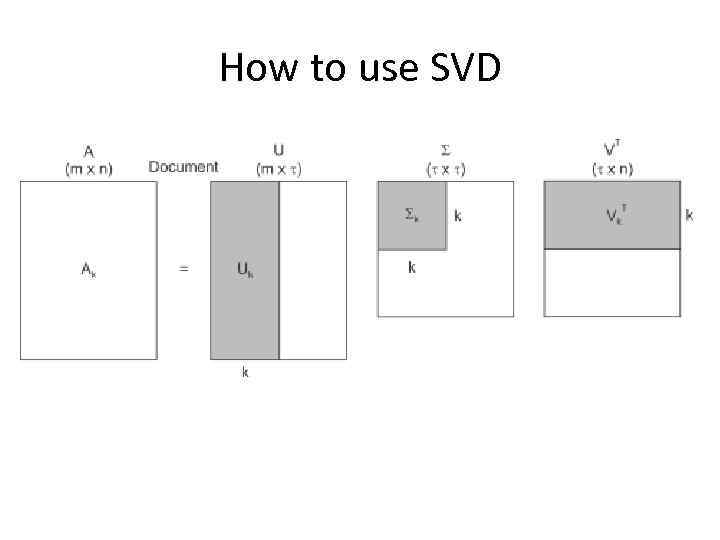 How to use SVD
How to use SVD
 Plan 1. 2. 3. 4. 5. 6. Linear classification Semi-supervised learning Linear regression Decision trees Ensemble methods Bonus-track
Plan 1. 2. 3. 4. 5. 6. Linear classification Semi-supervised learning Linear regression Decision trees Ensemble methods Bonus-track


