ПР А В И Л А О Д Н О Г О И Д В У Х ЛОЖНЫХ ПОЛОЖЕНИЙ. Выполнил студент 3 -го курса фак-та МИи. Ф Соловьёв Виктор.
ПЛАН. v Правило одного ложного положения. v Правило двух ложных положений. v Задачи для самостоятельного решения.
ПРАВИЛО ОДНОГО ЛОЖНОГО ПОЛОЖЕНИЯ. v
Задача 1. v
ЗАМЕЧАНИЕ ! v Это же значение неизвестного получается для любого другого числа , взятого в качестве «ложного числа положения» . v В случае когда коэффициент при неизвестном составлял сумму нескольких дробей , то в качестве ложного положения египтяне брали число, кратное их знаменателям, что облегчало задачу.
Задача 2. v
v
Задача 3. v Найти число, которое взято пять раз и сложенное с числом 3, дает 63.
ПРАВИЛО ДВУХ ЛОЖНЫХ ПОЛОЖЕНИЙ. v
v
v Правило давало удобный алгоритм для решения любых сколь угодно сложных задач, условия которых аналитически могли быть записаны уравнениями первой степени с одним неизвестным, причем не требовалось ни анализа задачи, ни ее представления в форме алгебраического уравнения. По этому правилу в китайском трактате « Математика в девяти книгах» (2 в до н. э. ) решались многие задачи. Погрешность книгах» (2 в до н. э. ) называлась «избытком» если «ложное положение» давало больший, чем в условии, результат. В случае меньшего – «недостатком»
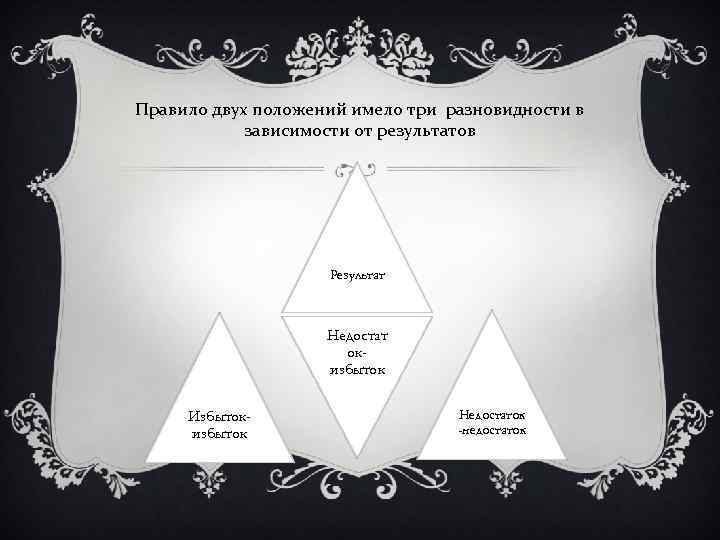Правило двух положений имело три разновидности в зависимости от результатов Результат Недостат окизбыток Избытокизбыток Недостаток -недостаток
v
Задача 1. v
СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ С НЕСКОЛЬКИМИ НЕИЗВЕСТНЫМИ. v
Генрих Крамер (нем. Heinrich Kramer, также известный как Генрикус Инститор (лат. Henricus Institor) v
v
Задача 4. v Сообща покупают барана. Если каждый человек внесет по 5, то недостаток равен 45. Если по 7, то недостаток равен 3. Спрашивается, каково количество людей и стоимость барана?
Задача 5. v Сообща покупают курицу. Если каждый человек внесет по 9, то избыток равен 11. Если каждый человек внесет по 6, то недостаток равен 16. Спрашивается кол-во людей и стоимость курицы.
Задача 6. Сообща покупают собаку. Если каждый человек внесет по 5, то недостаток равен 90. Если каждый внесет по 50, то, как раз хватит. Спрашивается кол-во человек и стоимость собаки.
Задача 7. Пять буйволов и два барана стоят 10 ланов золота. Два буйвола и пять баранов стоят 8 ланов золота. Сколько стоят буйвол и баран в отдельности?
v Коста ибн Лука ал – Балабаки (Ⅹ в. ) написал специальное сочинение, посвященное этому способу решения задач в трактате «О доказательстве действий при исчислении двух ошибок» он дал два вывода правила: чисто арифметический и опирающийся на средства геометрической алгебры древних греков. Ибн ал – Банна (13 -14 в. ) дал подробное описание метода под названием «правило чаш весов» в «Кратком изложении арифметических действий»
v Его формулировка такова: «Рисуй весы. Над точкой опоры пиши число, которое по условию задачи получается после действий над искомым числом. На чашке весов пиши оба предположения. Отклонения «больше» пиши под весами, отклонения «меньше» -над весами. Произведи умножение накрест предположений и отклонений. Если отклонения записаны оба по сторону от весов, то надо брать разности произведений и отклонений; если же отклонения записаны по разные стороны, то надо брать суммы произведений и отклонений»
Задача 8. v Найдите число, которое будучи взято десять раз и сложенное с ушестеренным числом, дает 50.
v
v
Задачи для самостоятельного решения. 1. Куча. Две трети ее, ее вторая часть, ее седьмая часть и ее целое составляют 33. Что есть куча? 2. Некто взял из сокровищницы 13 -ю часть богатства. Другой взял из нее семнадцатую часть остатка , оставив 150. Сколько было в сокровищнице первоначально? 3. Найти число, которое, будучи взято семь раз и сложено с ушестеренным числом, дает 25. 4. Сообща покупают вещь. Если каждый человек внесет по 8, то избыток будет 3. Если каждый внесет по 7, то недостаток равен 4. Спрашивается кол-во людей и стоимость вещи.
Задачи для самостоятельного решения. 5. Имеется стена толщиной в 5 чи. Две крысы, находясь по разные стороны стены, прогрызают отверстие навстречу другу. Большая крыса за первый день прогрызает 1 чи, маленькая тоже. Большая крыса каждый следующий день прогрызает в два раза больше, чем накануне, маленькая –в два раза меньше. Через сколько дней они встретятся? 6. Богатство первого и второго, взятые вместе составляют 13, второго и третьего , взятые вместе -14, богатство первого и третьего -15. Назови богатство каждого.