Пояснения к задачам темы 4 4. 8

Пояснения к задачам темы 4

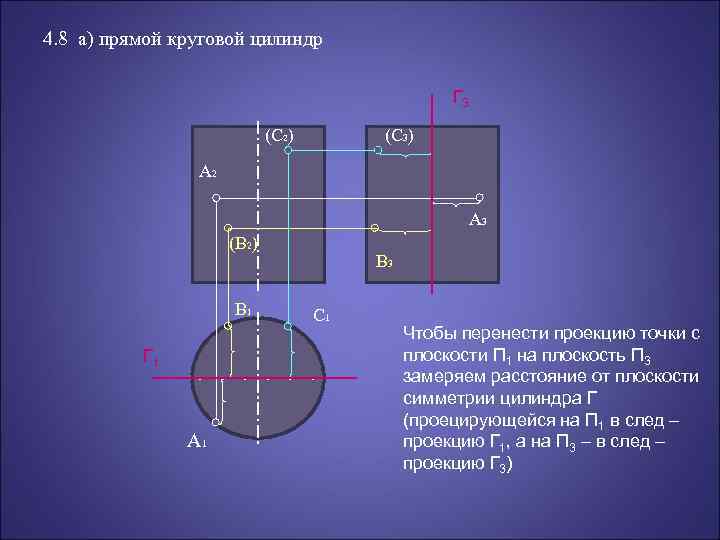4. 8 а) прямой круговой цилиндр Г 3 (C 2) (C 3) A 2 A 3 (B 2) B 1 Г 1 A 1 B 3 C 1 Чтобы перенести проекцию точки с плоскости П 1 на плоскость П 3 замеряем расстояние от плоскости симметрии цилиндра Г (проецирующейся на П 1 в след – проекцию Г 1, а на П 3 – в след – проекцию Г 3)

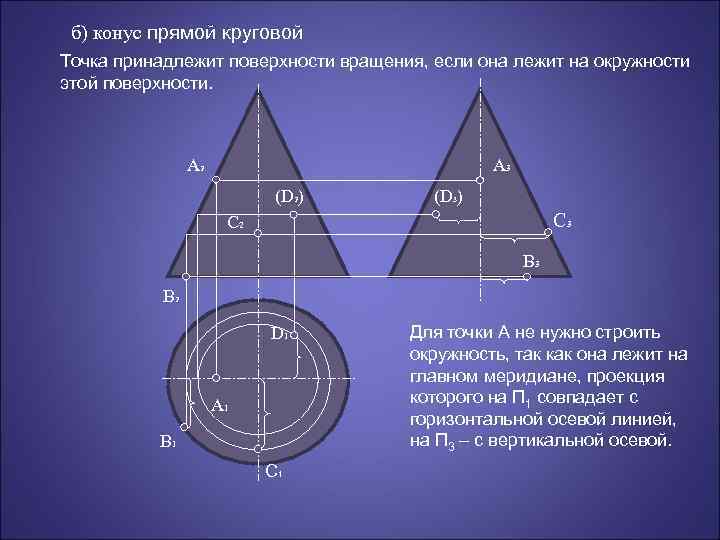б) конус прямой круговой Точка принадлежит поверхности вращения, если она лежит на окружности этой поверхности. A 2 A 3 (D 2) (D 3) C 3 C 2 B 3 B 2 D 1 A 1 B 1 C 1 Для точки А не нужно строить окружность, так как она лежит на главном меридиане, проекция которого на П 1 совпадает с горизонтальной осевой линией, на П 3 – с вертикальной осевой.

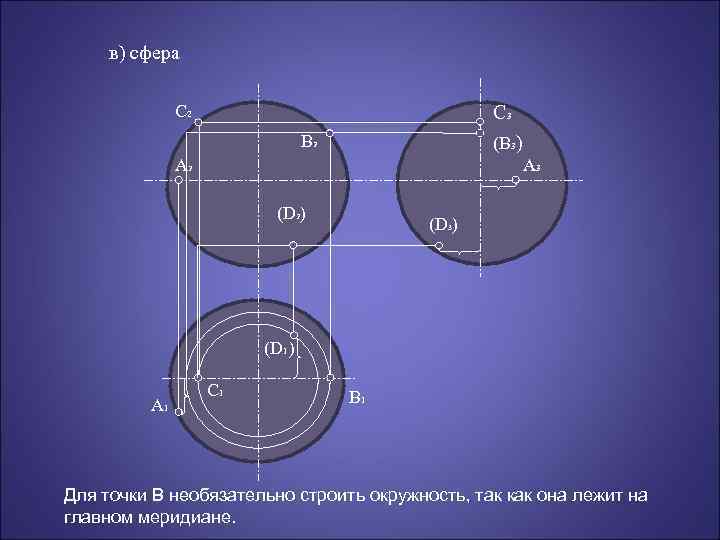в) сфера C 2 C 3 B 2 (B 3) A 2 A 3 (D 2) (D 3) (D 1 ) A 1 C 1 B 1 Для точки В необязательно строить окружность, так как она лежит на главном меридиане.

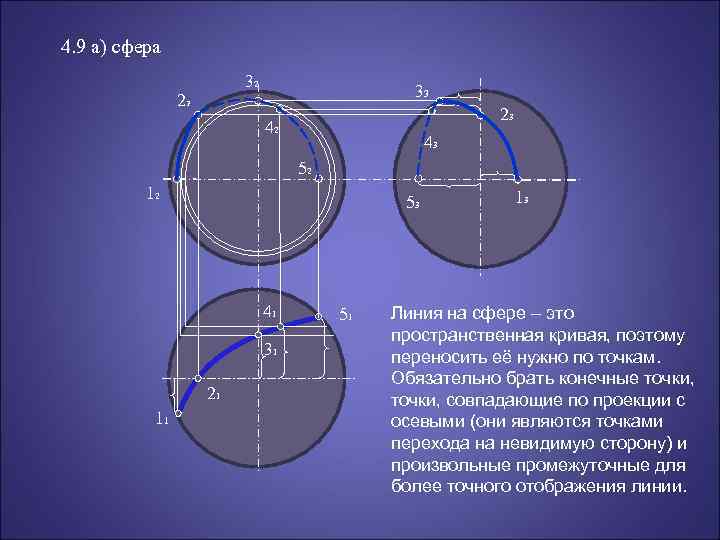4. 9 а) сфера 32 22 33 23 42 43 52 12 53 41 31 21 11 51 13 Линия на сфере – это пространственная кривая, поэтому переносить её нужно по точкам. Обязательно брать конечные точки, совпадающие по проекции с осевыми (они являются точками перехода на невидимую сторону) и произвольные промежуточные для более точного отображения линии.

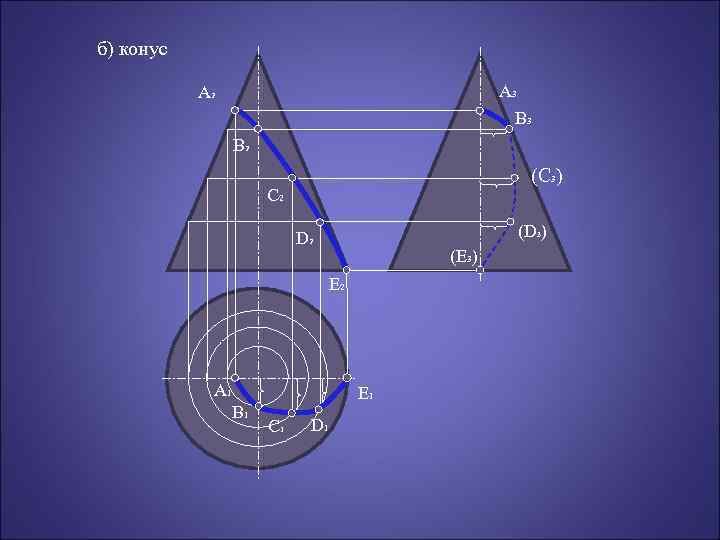б) конус A 3 B 3 A 2 B 2 (C 3) C 2 (D 3) D 2 (Е 3) Е 2 A 1 B 1 Е 1 С 1 D 1