L4.ppt
- Количество слайдов: 33
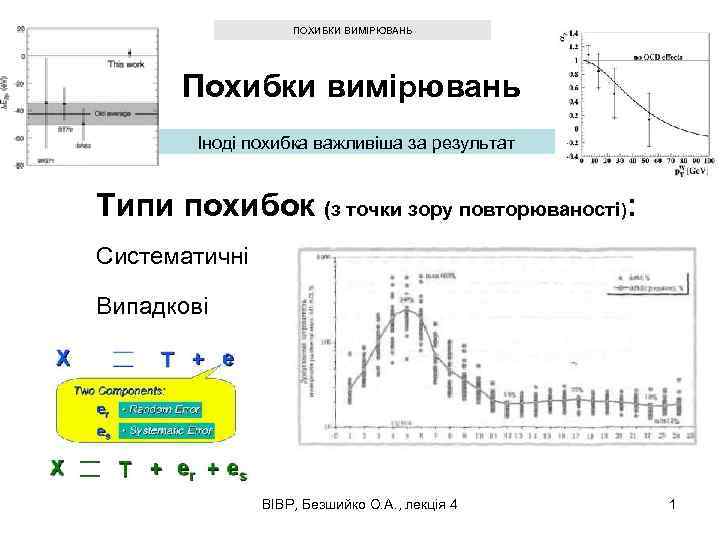
ПОХИБКИ ВИМІРЮВАНЬ Похибки вимірювань Іноді похибка важливіша за результат Типи похибок (з точки зору повторюваності): Систематичні Випадкові ВІВР, Безшийко О. А. , лекція 4 1
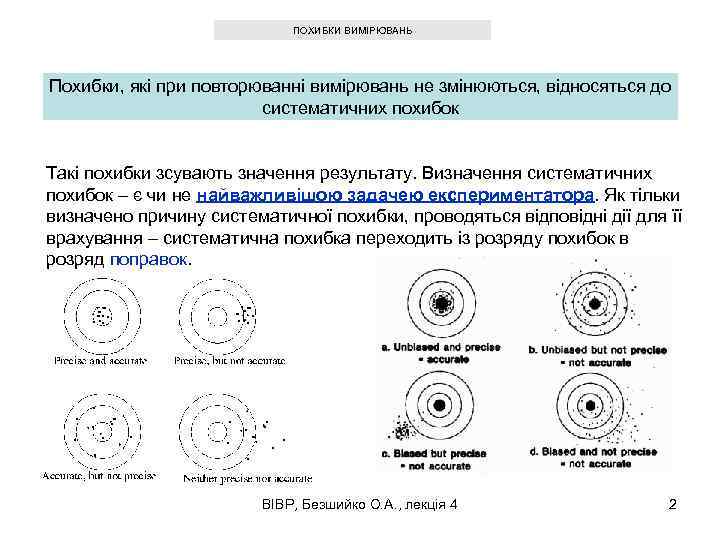
ПОХИБКИ ВИМІРЮВАНЬ Похибки, які при повторюванні вимірювань не змінюються, відносяться до систематичних похибок Такі похибки зсувають значення результату. Визначення систематичних похибок – є чи не найважливішою задачею експериментатора. Як тільки визначено причину систематичної похибки, проводяться відповідні дії для її врахування – систематична похибка переходить із розряду похибок в розряд поправок. ВІВР, Безшийко О. А. , лекція 4 2
ПОХИБКИ ВИМІРЮВАНЬ Оцінені дані ВІВР, Безшийко О. А. , лекція 4 3
ПОХИБКИ ВИМІРЮВАНЬ Оцінені дані ВІВР, Безшийко О. А. , лекція 4 4
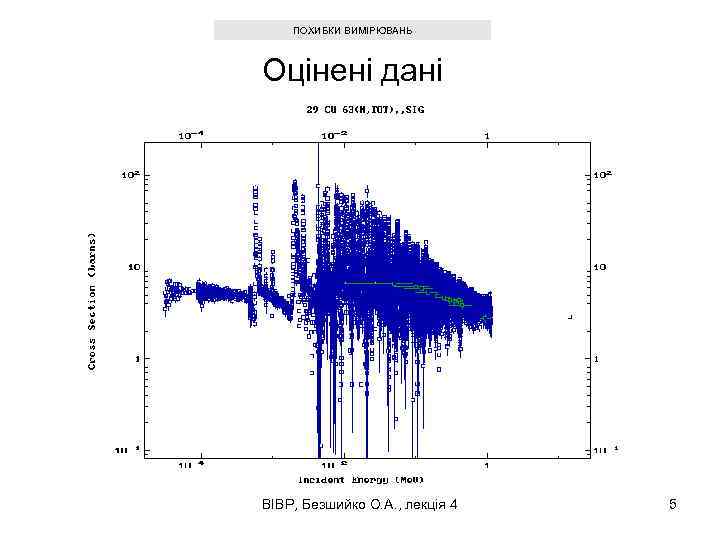
ПОХИБКИ ВИМІРЮВАНЬ Оцінені дані ВІВР, Безшийко О. А. , лекція 4 5
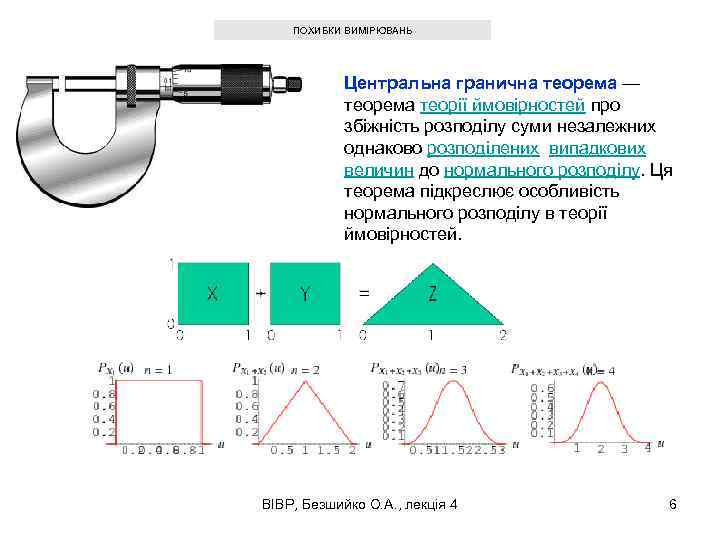
ПОХИБКИ ВИМІРЮВАНЬ Центральна гранична теорема — теорема теорії ймовірностей про збіжність розподілу суми незалежних однаково розподілених випадкових величин до нормального розподілу. Ця теорема підкреслює особливість нормального розподілу в теорії ймовірностей. ВІВР, Безшийко О. А. , лекція 4 6

ПОХИБКИ ВИМІРЮВАНЬ Способи боротьби із систематичними похибками 1. Найбільш стандартний універсальний спосіб знаходити систематичні похибки і зводити їх до статистичних – це багатократне повторення експерименту з максимально можливою зміною умов експерименту, які не є з точки зору експериментатора і фізичних міркувань визначальними (їх зміна не повинна впливати на результат) для експерименту, але в реальності вони можуть мати такий неконтрольований вплив. 2. Другий основний метод зменшення статистичних похибок – планування і побудова такого алгоритму вимірювань та обробки даних, при якому систематичні похибки будуть мінімізуватися. ВІВР, Безшийко О. А. , лекція 4 7
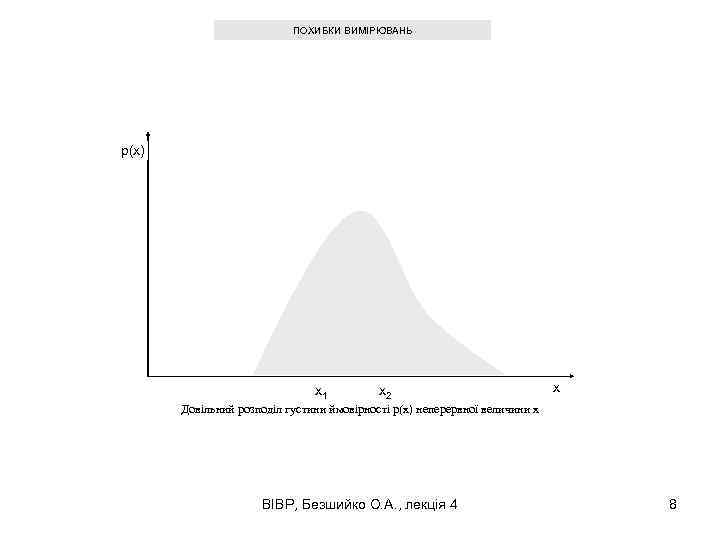
ПОХИБКИ ВИМІРЮВАНЬ p(x) x 1 x 2 x Довільний розподіл густини ймовірності p(x) неперервної величини x ВІВР, Безшийко О. А. , лекція 4 8
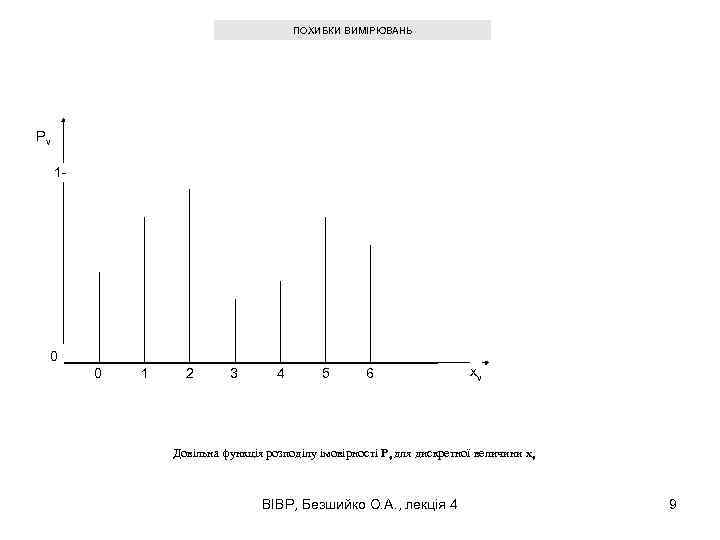
ПОХИБКИ ВИМІРЮВАНЬ Pν 1 - 0 0 1 2 3 4 5 6 xν Довільна функція розподілу імовірності Pν для дискретної величини xν ВІВР, Безшийко О. А. , лекція 4 9

ПОХИБКИ ВИМІРЮВАНЬ Каденко І. М. , Плюйко В. А. , Основи методів оцінок статистичних даних та функцій їх розподілу. -К: ВПЦ “Київський університет”, 2003. -145 с. Тейлор Дж. , Введение в теорию ошибок. -М. : Мир, 1985. -272 с. ВІВР, Безшийко О. А. , лекція 4 10

ПОХИБКИ ВИМІРЮВАНЬ Найпростіше визначення імовірності появи ν-ї реалізації дискретної статистичної величини можна представити як відносну частоту появи ν -ї реалізації в такому вигляді де M – повна кількість вимірювань (випробувань), mν – кількість вимірювань (випробувань), у яких з’явилась ν-та реалізація xν випадкової величини, N – загальна кількість реалізацій. При скінченних M відносна частота Pν є випадковою і називається вибірковою відносною частотою появи ν-ї реалізації. Неважко помітити, що Pν завжди не більше одиниці і - це умова нормування. Сукупність значень ймовірностей Pν для всіх можливих реалізацій ν=1, …, N називається законом розподілу випадкової дискретної величини. Він є повною характеристикою випадкової величини. ВІВР, Безшийко О. А. , лекція 4 11

ПОХИБКИ ВИМІРЮВАНЬ Імовірність знаходження реалізації неперервної випадкової величини в інтервалі визначається формулою де M – повна кількість вимірювань, m 12 – кількість знаходжень реалізацій ξ в даному інтервалі. У випадку, коли , а , ймовірність , що розглядається як функція змінної x, називається функцією розподілу випадкової величини, або інтегральним законом розподілу: ВІВР, Безшийко О. А. , лекція 4 12

ПОХИБКИ ВИМІРЮВАНЬ Густина p(x) є імовірністю появи реалізацій величини ξ в інтервалі , віднесену до довжини Δx цього інтервалу при : де Δmx – кількість знаходжень реалізацій ξ в даному інтервалі. ВІВР, Безшийко О. А. , лекція 4 13
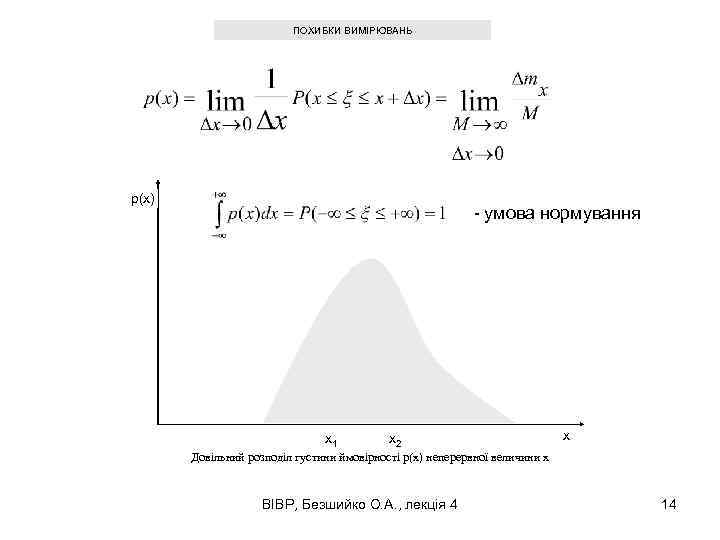
ПОХИБКИ ВИМІРЮВАНЬ p(x) - умова нормування x 1 x 2 x Довільний розподіл густини ймовірності p(x) неперервної величини x ВІВР, Безшийко О. А. , лекція 4 14

ПОХИБКИ ВИМІРЮВАНЬ p(x) визначає ймовірність p(x)dx того, що випадкова величина при вимірюванні в однакових умовах набуде значень з інтервалу Закон розподілу випадкової неперервної величини є повною характеристикою цієї величини Часто достатньо знати тільки деякі важливі параметри розподілу Початковий момент першого порядку випадкової величини Інші назви - математичне сподівання, або теоретичне середнє значення випадкової величини ВІВР, Безшийко О. А. , лекція 4 15

ПОХИБКИ ВИМІРЮВАНЬ Центральні незмішані моменти другого порядку (дисперсії випадкових величин ) середньоквадратичне відхилення інші назва – стандартне відхилення, стандартна похибка ВІВР, Безшийко О. А. , лекція 4 16
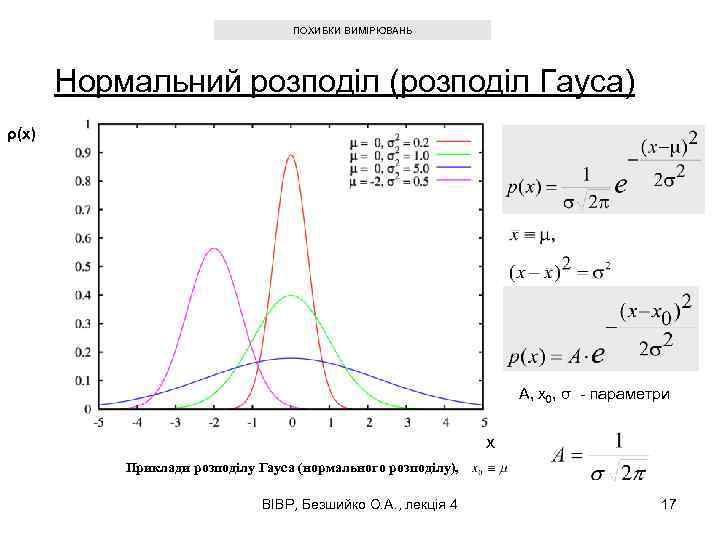
ПОХИБКИ ВИМІРЮВАНЬ Нормальний розподіл (розподіл Гауса) ρ(x) A, x 0, σ - параметри x Приклади розподілу Гауса (нормального розподілу), ВІВР, Безшийко О. А. , лекція 4 17

ПОХИБКИ ВИМІРЮВАНЬ - умова нормування ВІВР, Безшийко О. А. , лекція 4 18
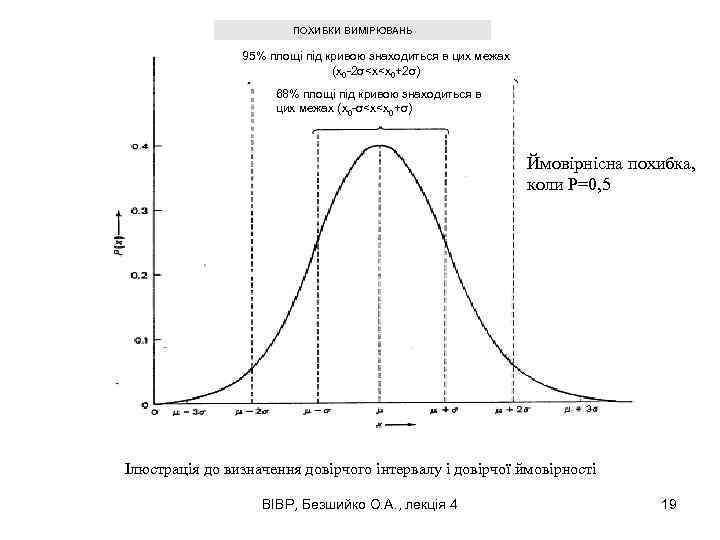
ПОХИБКИ ВИМІРЮВАНЬ 95% площі під кривою знаходиться в цих межах (x 0 -2σ<x<x 0+2σ) 68% площі під кривою знаходиться в цих межах (x 0 -σ<x<x 0+σ) Ймовірнісна похибка, коли P=0, 5 Ілюстрація до визначення довірчого інтервалу і довірчої ймовірності ВІВР, Безшийко О. А. , лекція 4 19

ПОХИБКИ ВИМІРЮВАНЬ - Вибіркове середнє (найкраща оцінка математичного сподівання x 0) Вибіркове середнє при прямує до математичного сподівання x 0 Вибіркове середнє при прямує до нормального розподілу із математичним сподіванням x 0 та дисперсією σ2/n , де σ2 – дисперсія розподілу випадкової величини xk - (вибіркова дисперсія) найкраща оцінка дисперсії випадкової величини Вибіркова дисперсія прямує до теоретичної дисперсії ( при ) ВІВР, Безшийко О. А. , лекція 4 20

ПОХИБКИ ВИМІРЮВАНЬ Вибіркове середнє при прямує до нормального розподілу із математичним сподіванням x 0 та дисперсією σ2/n , де σ2 – дисперсія розподілу випадкової величини xk - (вибіркова дисперсія) найкраща оцінка дисперсії випадкової величини А отже дисперсія вибіркового середнього при прямує до: ВІВР, Безшийко О. А. , лекція 4 21

ПОХИБКИ ВИМІРЮВАНЬ дисперсія вибіркового середнього Середньоквадратична похибка середнього значення Середньоквадратична похибка випадкової величини (окремого значення) ВІВР, Безшийко О. А. , лекція 4 22

ПОХИБКИ ВИМІРЮВАНЬ Розподіл Пуассона Для дискретної величини N Для розподілу Пуассона математичне сподівання і дисперсія збігаються та дорівнюють параметру μ (відповідно середньоквадратична похибка ) ВІВР, Безшийко О. А. , лекція 4 23

ПОХИБКИ ВИМІРЮВАНЬ Розподіл Пуассона Для виконання закону Пуассона необхідні такі умови: 1. Імовірність появи події в момент часу t не залежить від попереднього часу і кількості подій, що відбувалась раніш (незалежність подій). 2. Імовірність появи окремої події протягом малого інтервалу часу δt зростає зі сталою швидкістю (імовірністю в одиницю часу) λ, тобто поява окремої події в інтервалі часу (t, t+ δt) дорівнює λδt. 3. Імовірність появи двох або більшої кількості подій за той же проміжок часу (t, t+ δt) дорівнює нулю. ВІВР, Безшийко О. А. , лекція 4 24
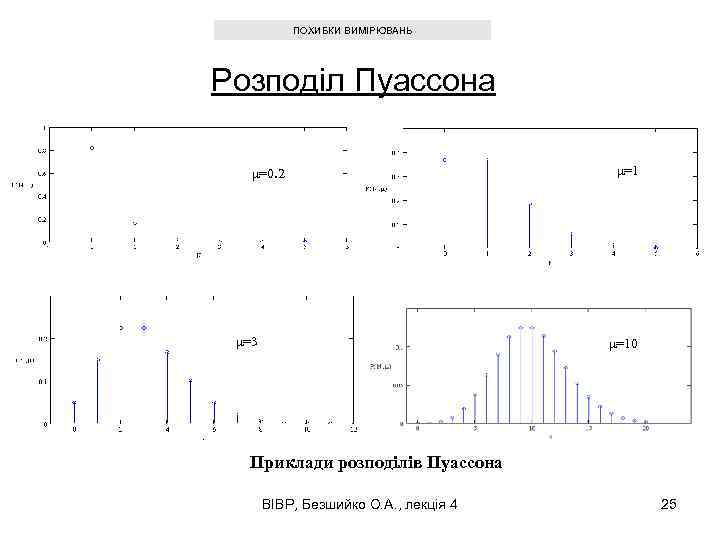
ПОХИБКИ ВИМІРЮВАНЬ Розподіл Пуассона μ=0. 2 μ=3 μ=10 Приклади розподілів Пуассона ВІВР, Безшийко О. А. , лекція 4 25

ПОХИБКИ ВИМІРЮВАНЬ 100100 =10200 100! =9. 3∙ 10157 e-100 =3. 7∙ 10 -44 Формула Стірлінга Для великих N, μ формула Пуассона добре апроксимується частинним випадком розподілу Гауса (дивіться, наприклад http: //nsu. ru/matlab/Exponenta_RU/educat/systemat/boziev/appl. asp. htm ): ВІВР, Безшийко О. А. , лекція 4 26

ПОХИБКИ ВИМІРЮВАНЬ Формула Стірлінга ВІВР, Безшийко О. А. , лекція 4 27

ПОХИБКИ ВИМІРЮВАНЬ ВІВР, Безшийко О. А. , лекція 4 28

ПОХИБКИ ВИМІРЮВАНЬ ВІВР, Безшийко О. А. , лекція 4 29

ПОХИБКИ ВИМІРЮВАНЬ Розклад в ряд Тейлора ВІВР, Безшийко О. А. , лекція 4 30

ПОХИБКИ ВИМІРЮВАНЬ ВІВР, Безшийко О. А. , лекція 4 31

ПОХИБКИ ВИМІРЮВАНЬ ВІВР, Безшийко О. А. , лекція 4 32

ПОХИБКИ ВИМІРЮВАНЬ при В цьому розподілі, на відміну від повного розподілу (в якому 3 параметри A, σ, x 0) 1 параметр μ – тому це частинний випадок розподілу Гауса ВІВР, Безшийко О. А. , лекція 4 33
L4.ppt