powerpointmaths com 3 2 Quality resources for the

powerpointmaths. com 3: 2 Quality resources for the mathematics classroom Reduce your workload and cut down planning Enjoy a new teaching experience Watch your students interest and enjoyment grow Key concepts focused on and driven home Over 100 files available with many more to come 1000’s of slides with nice graphics and effects. powerpointmaths. com Get ready to fly! © Powerpointmaths. com All rights reserved.

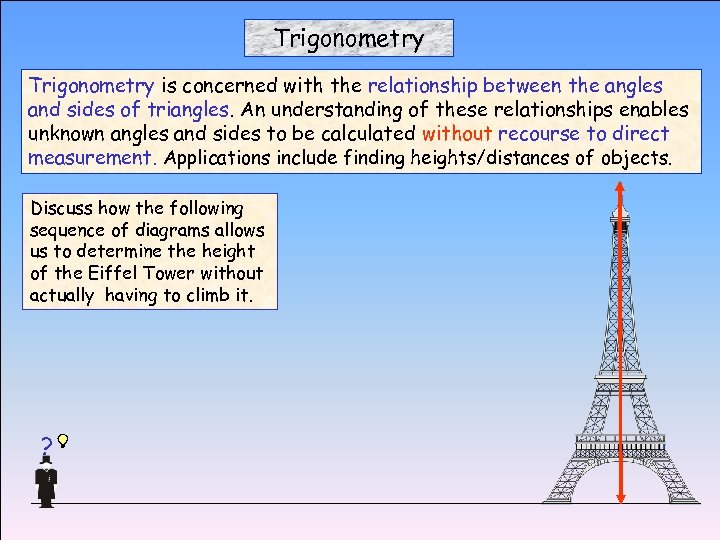Trigonometry is concerned with the relationship between the angles and sides of triangles. An understanding of these relationships enables unknown angles and sides to be calculated without recourse to direct measurement. Applications include finding heights/distances of objects. Discuss how the following sequence of diagrams allows us to determine the height of the Eiffel Tower without actually having to climb it. ?

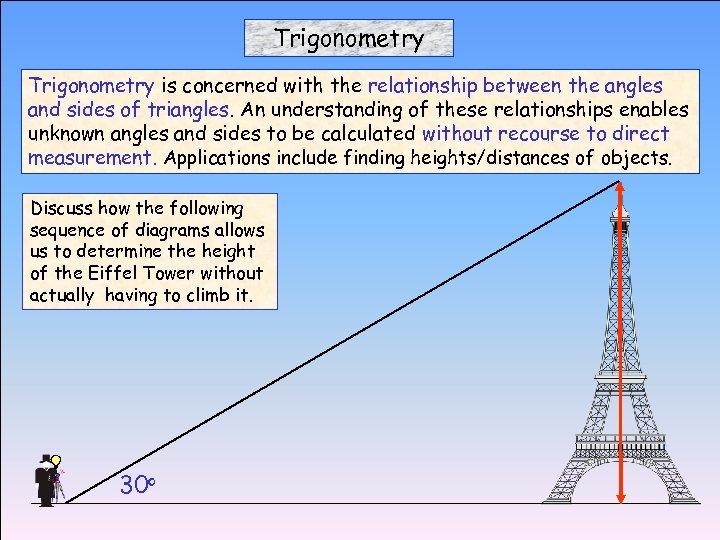Trigonometry is concerned with the relationship between the angles and sides of triangles. An understanding of these relationships enables unknown angles and sides to be calculated without recourse to direct measurement. Applications include finding heights/distances of objects. Discuss how the following sequence of diagrams allows us to determine the height of the Eiffel Tower without actually having to climb it. 30 o

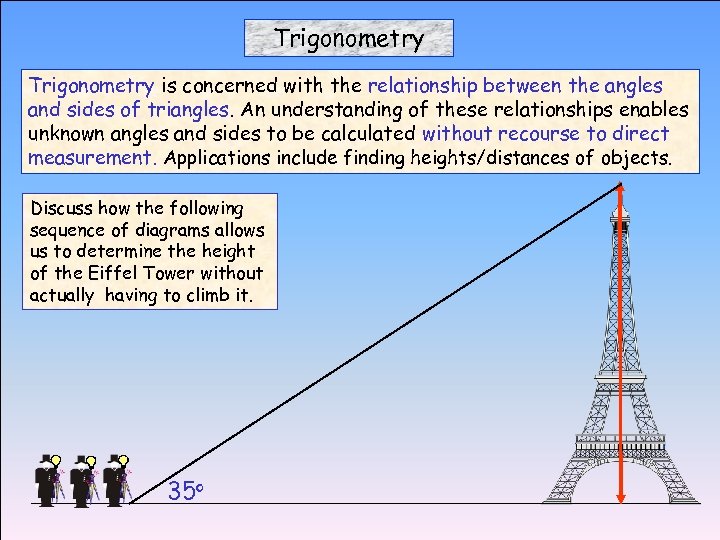Trigonometry is concerned with the relationship between the angles and sides of triangles. An understanding of these relationships enables unknown angles and sides to be calculated without recourse to direct measurement. Applications include finding heights/distances of objects. Discuss how the following sequence of diagrams allows us to determine the height of the Eiffel Tower without actually having to climb it. 35 o

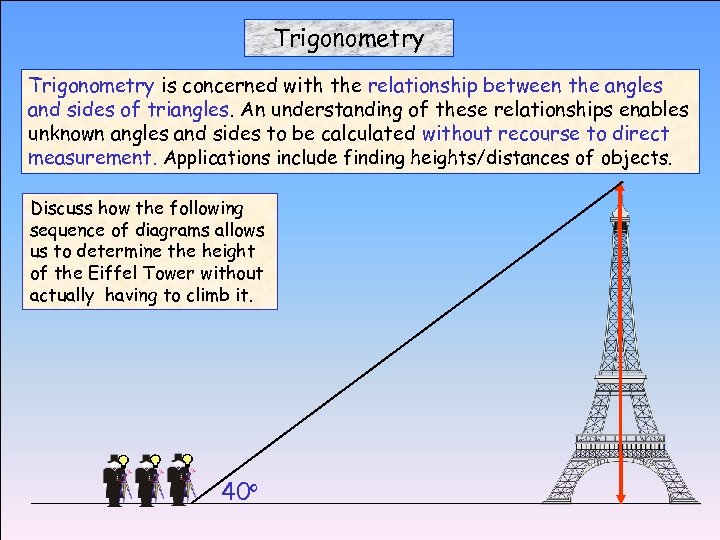Trigonometry is concerned with the relationship between the angles and sides of triangles. An understanding of these relationships enables unknown angles and sides to be calculated without recourse to direct measurement. Applications include finding heights/distances of objects. Discuss how the following sequence of diagrams allows us to determine the height of the Eiffel Tower without actually having to climb it. 40 o

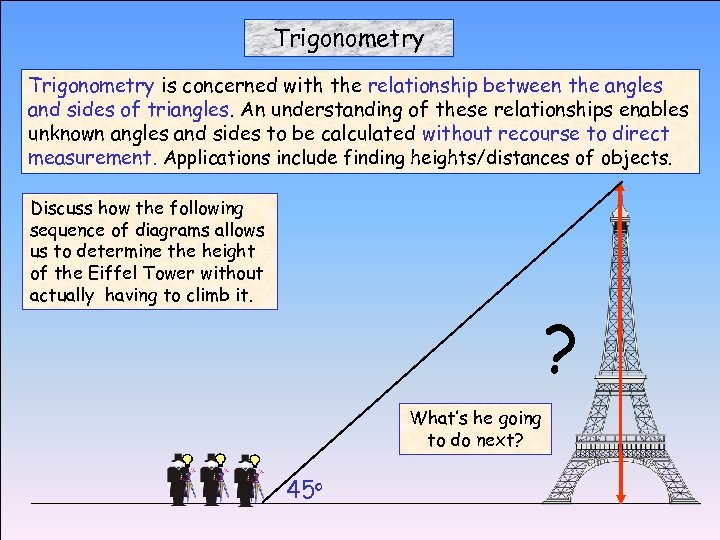Trigonometry is concerned with the relationship between the angles and sides of triangles. An understanding of these relationships enables unknown angles and sides to be calculated without recourse to direct measurement. Applications include finding heights/distances of objects. Discuss how the following sequence of diagrams allows us to determine the height of the Eiffel Tower without actually having to climb it. ? What’s he going to do next? 45 o

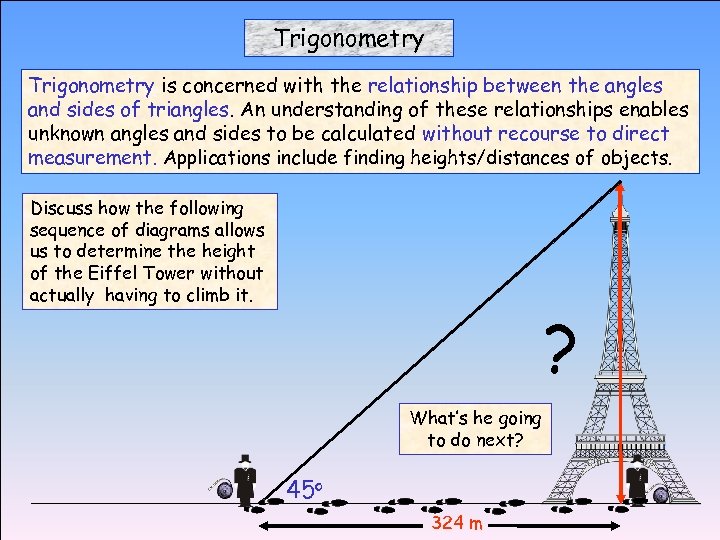Trigonometry is concerned with the relationship between the angles and sides of triangles. An understanding of these relationships enables unknown angles and sides to be calculated without recourse to direct measurement. Applications include finding heights/distances of objects. Discuss how the following sequence of diagrams allows us to determine the height of the Eiffel Tower without actually having to climb it. ? What’s he going to do next? 45 o 324 m

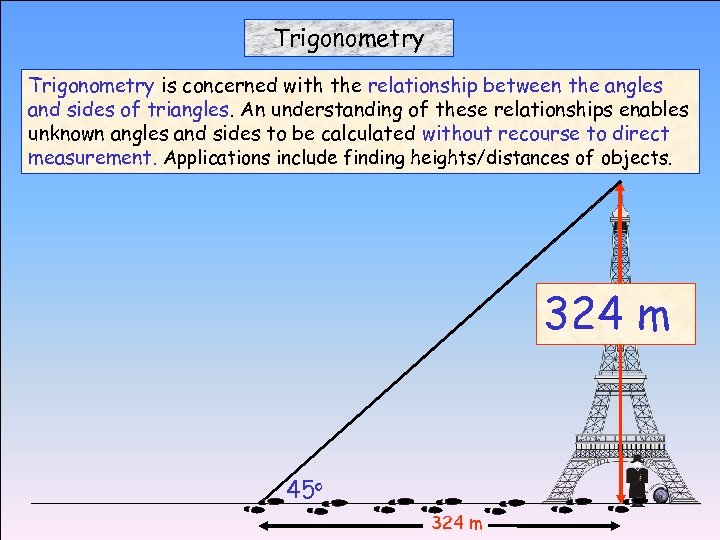Trigonometry is concerned with the relationship between the angles and sides of triangles. An understanding of these relationships enables unknown angles and sides to be calculated without recourse to direct measurement. Applications include finding heights/distances of objects. 324 m 45 o 324 m

Trigonometry Eiffel Tower Facts: • Designed by Gustave Eiffel. • Completed in 1889 to celebrate the centenary of the French Revolution. • Intended to have been dismantled after the 1900 Paris Expo. • Took 26 months to build. • The structure is very light and only weighs 7 300 tonnes. • 18 000 pieces, 2½ million rivets. • 1665 steps. • Some tricky equations had to be solved for its design. 324 m

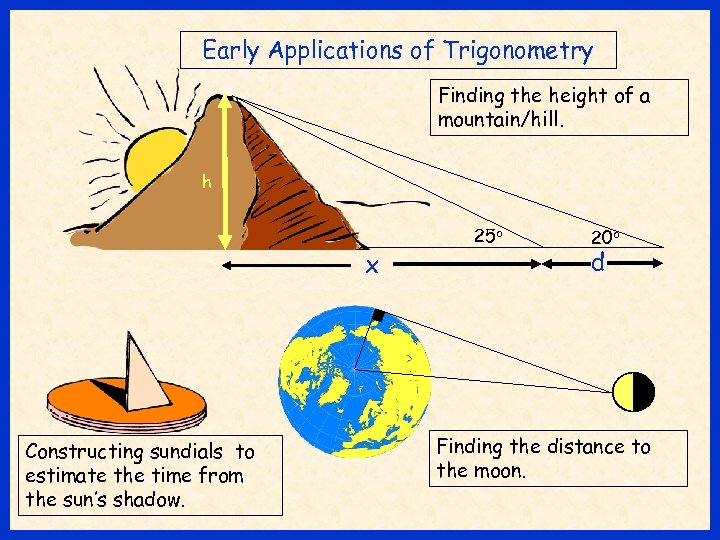Early Applications of Trigonometry Finding the height of a mountain/hill. h x Constructing sundials to estimate the time from the sun’s shadow. 25 o 20 o d Finding the distance to the moon.

Historically trigonometry was developed for work in Astronomy and Geography. Today it is used extensively in mathematics and many other areas of the sciences. • Surveying • Navigation • Physics • Engineering

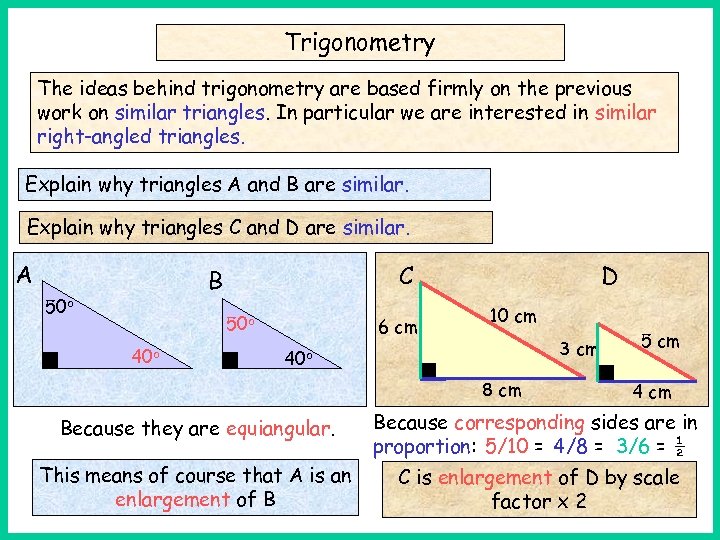Trigonometry The ideas behind trigonometry are based firmly on the previous work on similar triangles. In particular we are interested in similar right-angled triangles. Explain why triangles A and B are similar. Explain why triangles C and D are similar. A C A B 50 o 40 o 6 cm D 10 cm 3 cm 40 o 8 cm 5 cm 4 cm Because they are equiangular. Because corresponding sides are in proportion: 5/10 = 4/8 = 3/6 = ½ This means of course that A is an enlargement of B C is enlargement of D by scale factor x 2

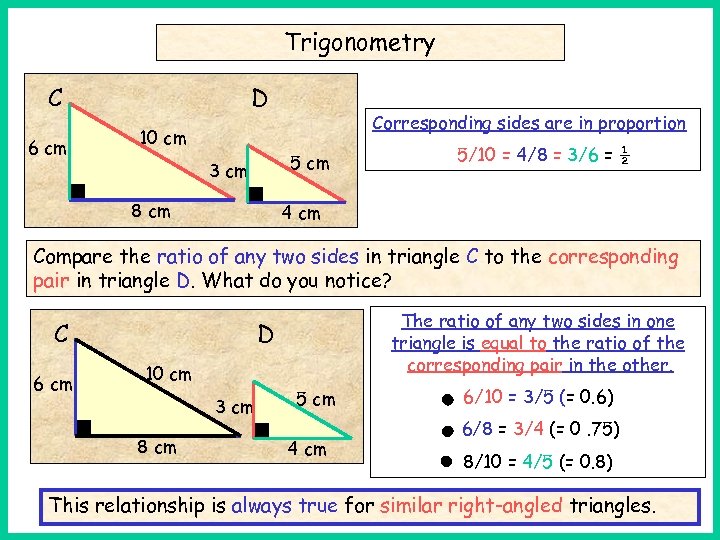Trigonometry C A 6 cm D Corresponding sides are in proportion 10 cm 5 cm 3 cm 8 cm 5/10 = 4/8 = 3/6 = ½ 4 cm Compare the ratio of any two sides in triangle C to the corresponding pair in triangle D. What do you notice? C A 6 cm The ratio of any two sides in one triangle is equal to the ratio of the corresponding pair in the other. D 10 cm 3 cm 8 cm 5 cm 4 cm 6/10 = 3/5 (= 0. 6) 6/8 = 3/4 (= 0. 75) 8/10 = 4/5 (= 0. 8) This relationship is always true for similar right-angled triangles.

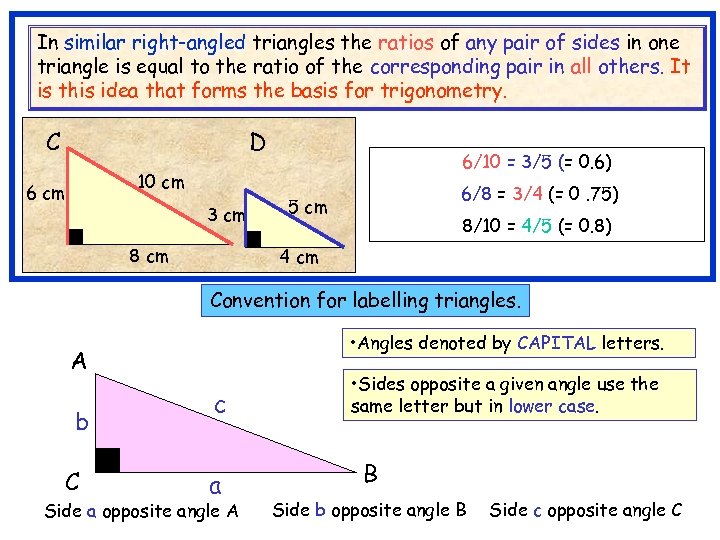In similar right-angled triangles the ratios of any pair of sides in one triangle is equal to the ratio of the corresponding pair in all others. It is this idea that forms the basis for trigonometry. C A D 6/10 = 3/5 (= 0. 6) 10 cm 6 cm 3 cm 8 cm 6/8 = 3/4 (= 0. 75) 5 cm 8/10 = 4/5 (= 0. 8) 4 cm Convention for labelling triangles. • Angles denoted by CAPITAL letters. A b C c a Side a opposite angle A • Sides opposite a given angle use the same letter but in lower case. B Side b opposite angle B Side c opposite angle C

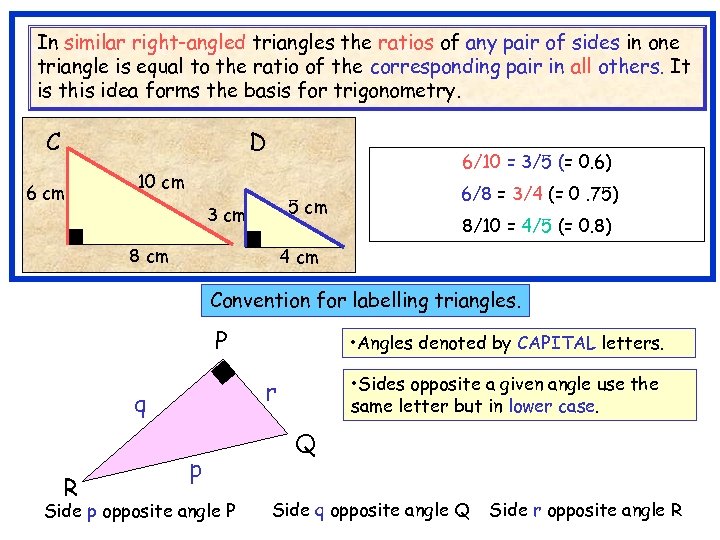In similar right-angled triangles the ratios of any pair of sides in one triangle is equal to the ratio of the corresponding pair in all others. It is this idea forms the basis for trigonometry. C A 6 cm D 6/10 = 3/5 (= 0. 6) 10 cm 5 cm 3 cm 8 cm 6/8 = 3/4 (= 0. 75) 8/10 = 4/5 (= 0. 8) 4 cm Convention for labelling triangles. P • Sides opposite a given angle use the same letter but in lower case. r q R • Angles denoted by CAPITAL letters. p Side p opposite angle P Q Side q opposite angle Q Side r opposite angle R

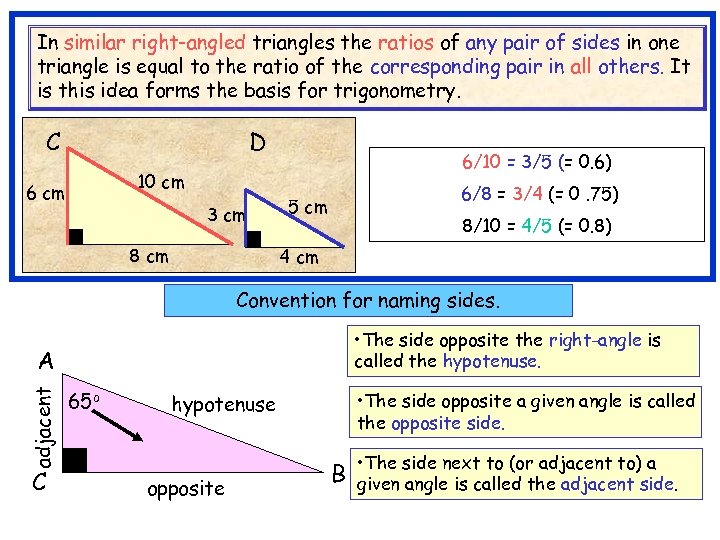In similar right-angled triangles the ratios of any pair of sides in one triangle is equal to the ratio of the corresponding pair in all others. It is this idea forms the basis for trigonometry. C A D 6/10 = 3/5 (= 0. 6) 10 cm 6 cm 3 cm 8 cm 6/8 = 3/4 (= 0. 75) 5 cm 8/10 = 4/5 (= 0. 8) 4 cm Convention for naming sides. • The side opposite the right-angle is called the hypotenuse. adjacent A C 65 o • The side opposite a given angle is called the opposite side. hypotenuse opposite B • The side next to (or adjacent to) a given angle is called the adjacent side.

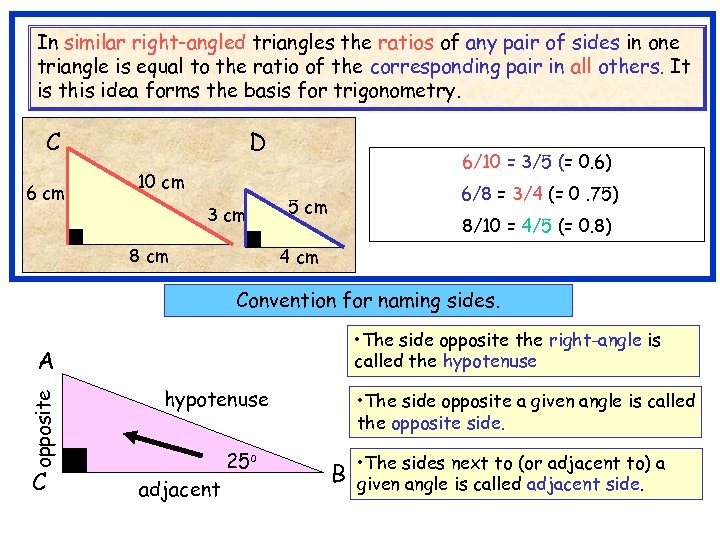In similar right-angled triangles the ratios of any pair of sides in one triangle is equal to the ratio of the corresponding pair in all others. It is this idea forms the basis for trigonometry. C A 6 cm D 6/10 = 3/5 (= 0. 6) 10 cm 3 cm 8 cm 6/8 = 3/4 (= 0. 75) 5 cm 8/10 = 4/5 (= 0. 8) 4 cm Convention for naming sides. • The side opposite the right-angle is called the hypotenuse opposite A C hypotenuse 25 o adjacent • The side opposite a given angle is called the opposite side. B • The sides next to (or adjacent to) a given angle is called adjacent side.

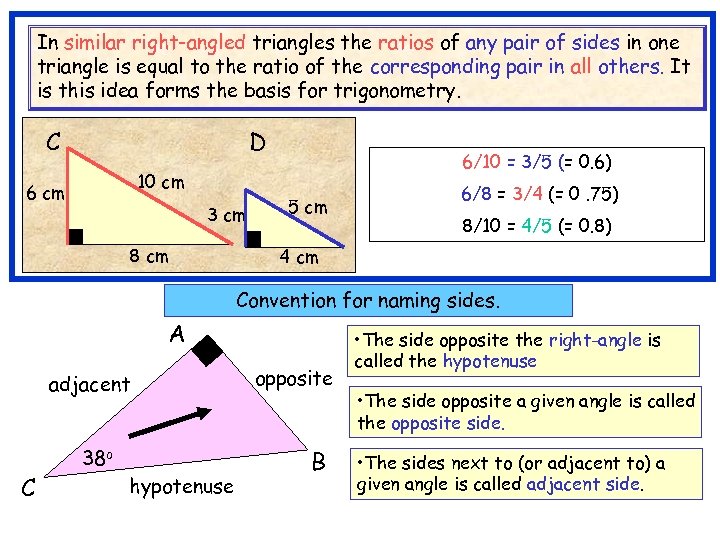In similar right-angled triangles the ratios of any pair of sides in one triangle is equal to the ratio of the corresponding pair in all others. It is this idea forms the basis for trigonometry. C A D 6/10 = 3/5 (= 0. 6) 10 cm 6 cm 3 cm 8 cm 5 cm 6/8 = 3/4 (= 0. 75) 8/10 = 4/5 (= 0. 8) 4 cm Convention for naming sides. A adjacent C 38 o hypotenuse opposite B • The side opposite the right-angle is called the hypotenuse • The side opposite a given angle is called the opposite side. • The sides next to (or adjacent to) a given angle is called adjacent side.

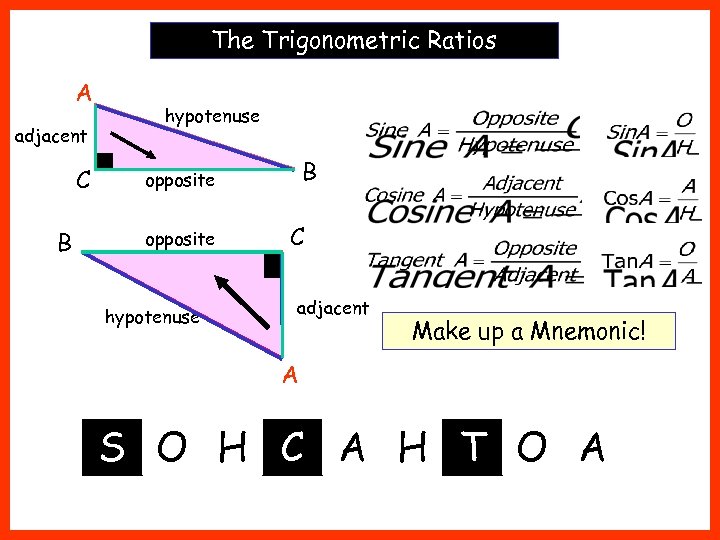The Trigonometric Ratios A adjacent C B hypotenuse B opposite hypotenuse C adjacent Make up a Mnemonic! A S O H C A H T O A

Make up a Mnemonic! S O H C A H T O A U A W P T I R R E S N P R L Y E Harry

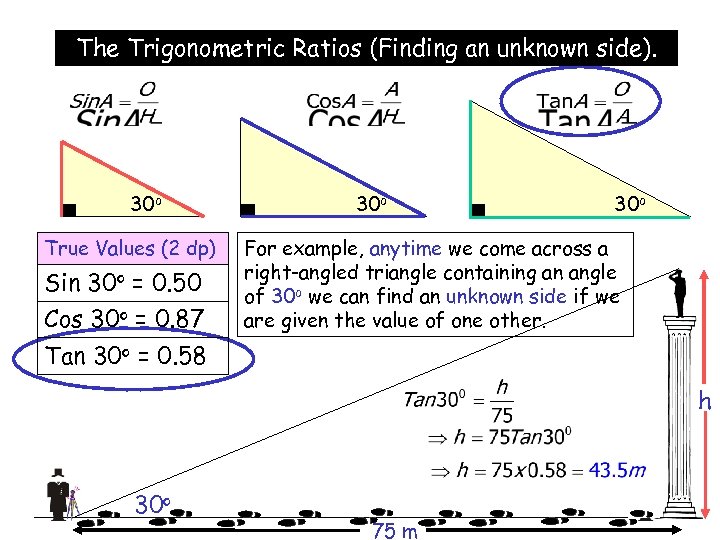The Trigonometric Ratios (Finding an unknown side). 30 o True Values (2 dp) Sin 30 o = 0. 50 Cos 30 o = 0. 87 30 o For example, anytime we come across a right-angled triangle containing an angle of 30 o we can find an unknown side if we are given the value of one other. Tan 30 o = 0. 58 h 30 o 75 m

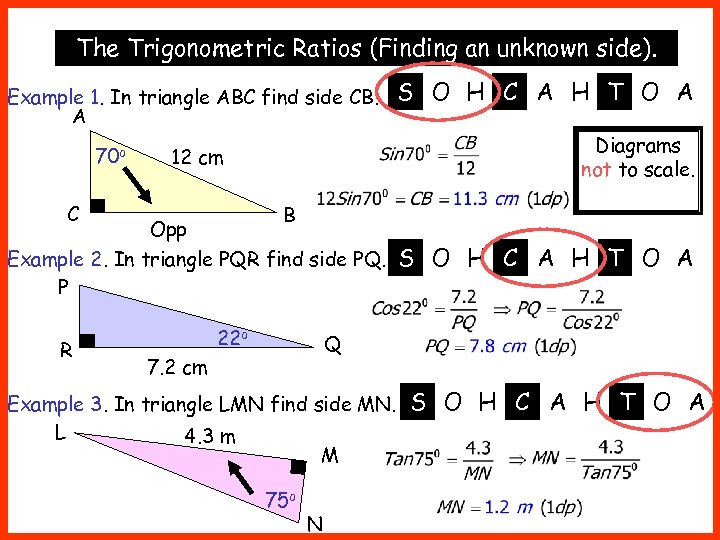The Trigonometric Ratios (Finding an unknown side). Example 1. In triangle ABC find side CB. A 70 o S O H C A H T O A Diagrams not to scale. 12 cm C B Opp Example 2. In triangle PQR find side PQ. P R 22 o S O H C A H T O A Q 7. 2 cm Example 3. In triangle LMN find side MN. L 4. 3 m M 75 o N S O H C A H T O A

The Trigonometric Ratios (Finding an unknown angle). True Values (2 dp) Sin 30 o = 0. 50 Cos 30 o = 0. 87 Tan 30 o = 0. 58 Anytime we come across a right-angled triangle containing 2 given sides we can calculate the ratio of the sides then look up (or calculate) the angle that corresponds to this ratio. S O H C A H T O A 43. 5 m xo 30 o 75 m

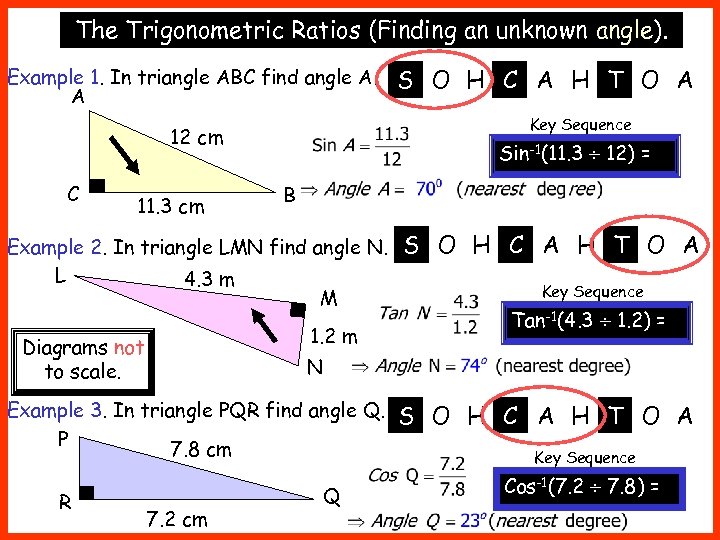The Trigonometric Ratios (Finding an unknown angle). Example 1. In triangle ABC find angle A. A Key Sequence 12 cm C 11. 3 cm Sin-1(11. 3 12) = B Example 2. In triangle LMN find angle N. L 4. 3 m M 1. 2 m Diagrams not to scale. S O H C A H T O A Key Sequence Tan-1(4. 3 1. 2) = N Example 3. In triangle PQR find angle Q. P 7. 8 cm R S O H C A H T O A 7. 2 cm Q S O H C A H T O A Key Sequence Cos-1(7. 2 7. 8) =

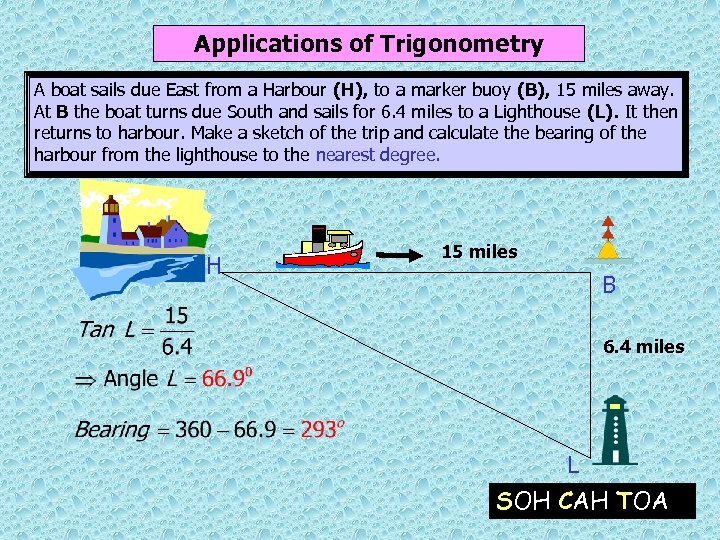Applications of Trigonometry A boat sails due East from a Harbour (H), to a marker buoy (B), 15 miles away. At B the boat turns due South and sails for 6. 4 miles to a Lighthouse (L). It then returns to harbour. Make a sketch of the trip and calculate the bearing of the harbour from the lighthouse to the nearest degree. H 15 miles B 6. 4 miles L SOH CAH TOA

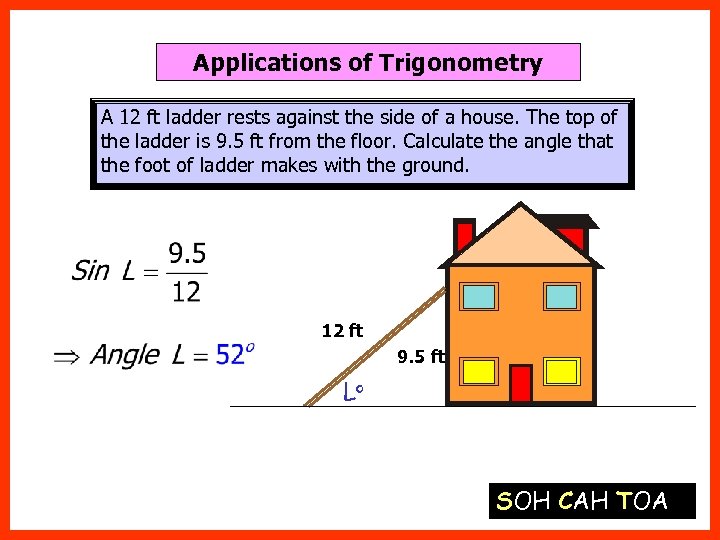Applications of Trigonometry A 12 ft ladder rests against the side of a house. The top of the ladder is 9. 5 ft from the floor. Calculate the angle that the foot of ladder makes with the ground. 12 ft 9. 5 ft Lo SOH CAH TOA

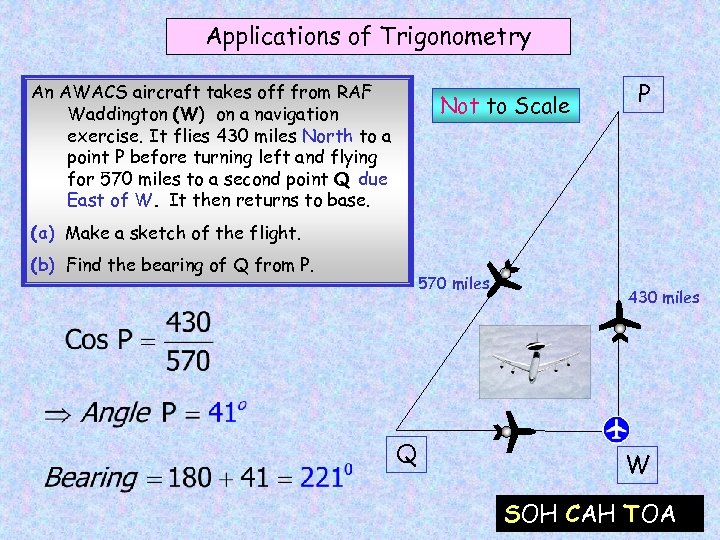Applications of Trigonometry An AWACS aircraft takes off from RAF Waddington (W) on a navigation exercise. It flies 430 miles North to a point P before turning left and flying for 570 miles to a second point Q due East of W. It then returns to base. Not to Scale P (a) Make a sketch of the flight. (b) Find the bearing of Q from P. 570 miles Q 430 miles W SOH CAH TOA

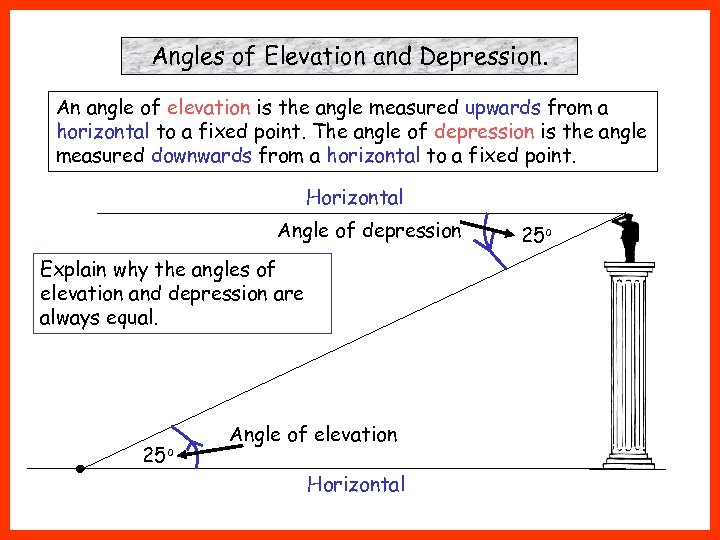Angles of Elevation and Depression. An angle of elevation is the angle measured upwards from a horizontal to a fixed point. The angle of depression is the angle measured downwards from a horizontal to a fixed point. Horizontal Angle of depression Explain why the angles of elevation and depression are always equal. 25 o Angle of elevation Horizontal 25 o

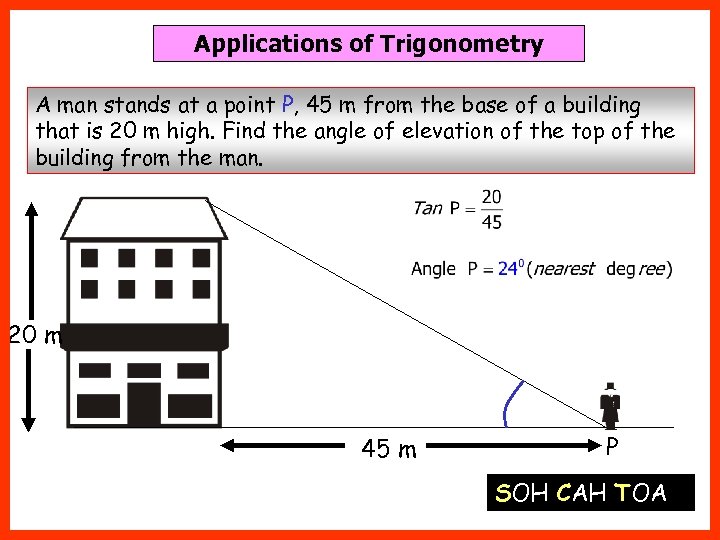Applications of Trigonometry A man stands at a point P, 45 m from the base of a building that is 20 m high. Find the angle of elevation of the top of the building from the man. 20 m 45 m P SOH CAH TOA

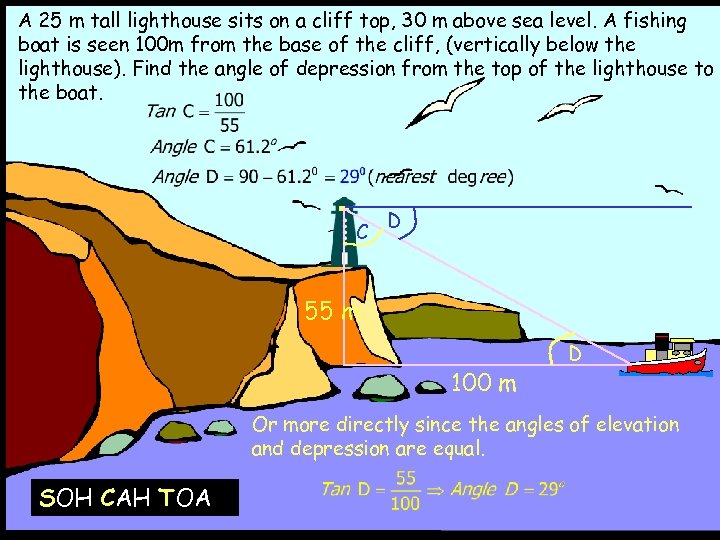A 25 m tall lighthouse sits on a cliff top, 30 m above sea level. A fishing boat is seen 100 m from the base of the cliff, (vertically below the lighthouse). Find the angle of depression from the top of the lighthouse to the boat. C D 55 m 100 m D Or more directly since the angles of elevation and depression are equal. SOH CAH TOA

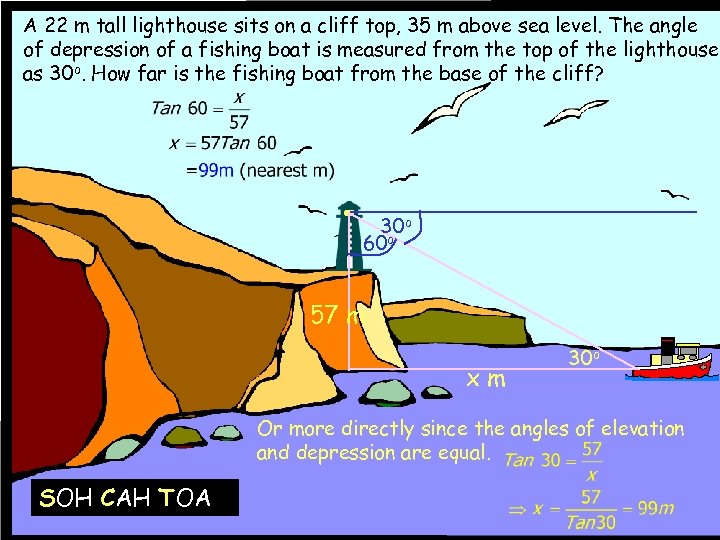A 22 m tall lighthouse sits on a cliff top, 35 m above sea level. The angle of depression of a fishing boat is measured from the top of the lighthouse as 30 o. How far is the fishing boat from the base of the cliff? 30 o 60 o 57 m xm 30 o Or more directly since the angles of elevation and depression are equal. SOH CAH TOA

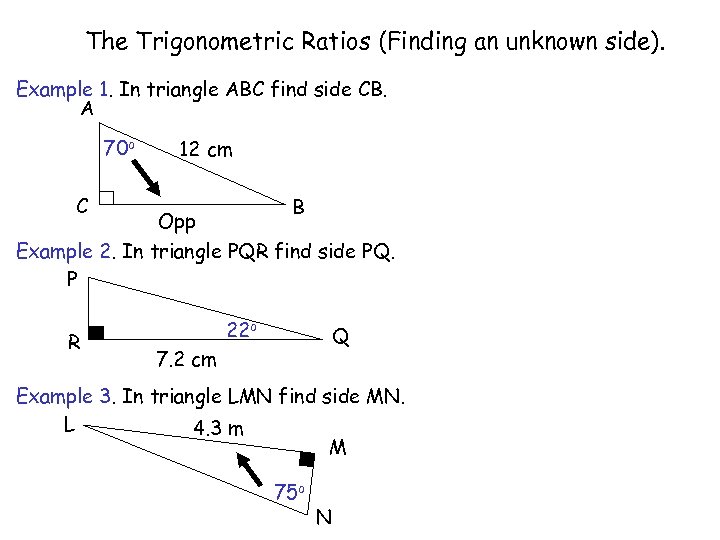The Trigonometric Ratios (Finding an unknown side). Example 1. In triangle ABC find side CB. A 70 o 12 cm C B Opp Example 2. In triangle PQR find side PQ. P R 22 o Q 7. 2 cm Example 3. In triangle LMN find side MN. L 4. 3 m M 75 o N Worksheet 2

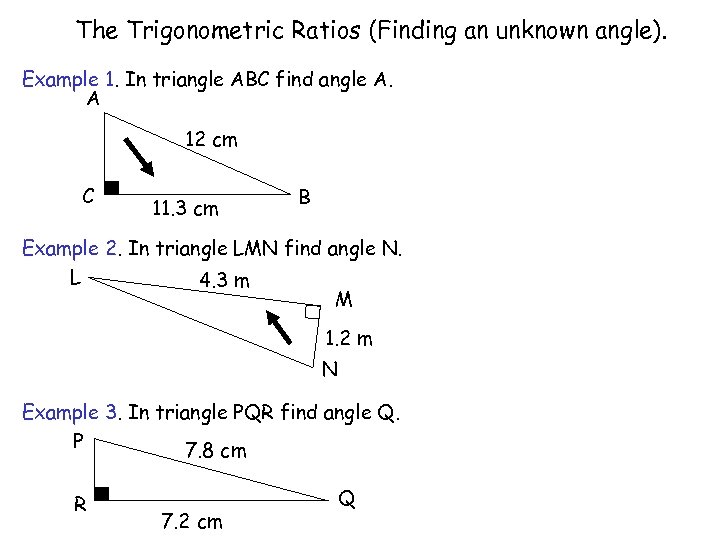The Trigonometric Ratios (Finding an unknown angle). Example 1. In triangle ABC find angle A. A 12 cm C 11. 3 cm B Example 2. In triangle LMN find angle N. L 4. 3 m M 1. 2 m N Example 3. In triangle PQR find angle Q. P 7. 8 cm R 7. 2 cm Q Worksheet 3