Повторение. Построить линейный угол двугранного угла ВАСК. Четырехугольник

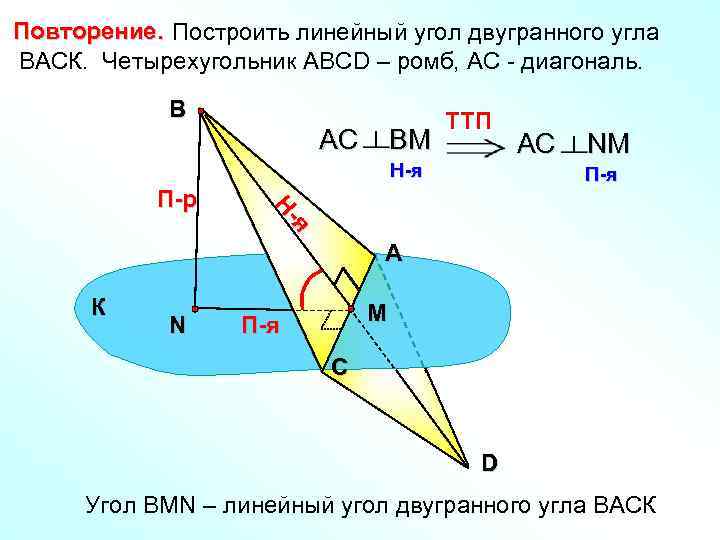Повторение. Построить линейный угол двугранного угла ВАСК. Четырехугольник АВСD – ромб, АС - диагональ. В АС ВМ TTП H-я NМ П-я я я Н-Н П-р АС А К N M П-я С D Угол ВMN – линейный угол двугранного угла ВАСК

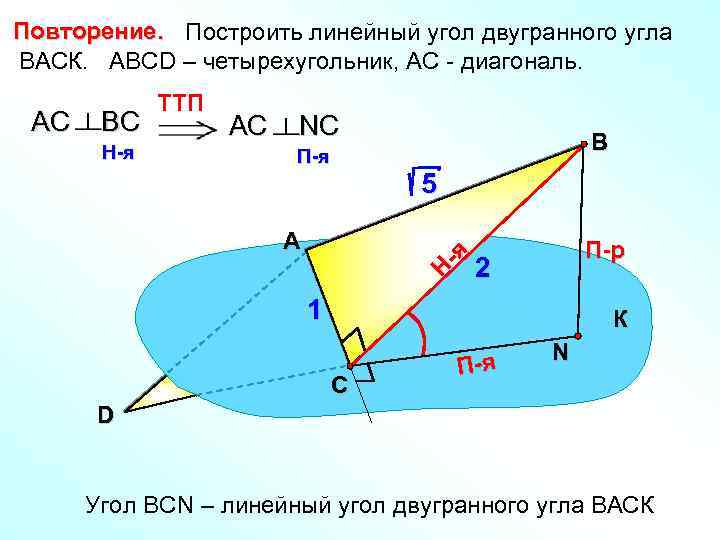Повторение. Построить линейный угол двугранного угла ВАСК. АВСD – четырехугольник, АС - диагональ. ВС H-я АС NС П-я В 5 А Н -я АС TTП П-р 2 1 К С П-я N D Угол ВСN – линейный угол двугранного угла ВАСК

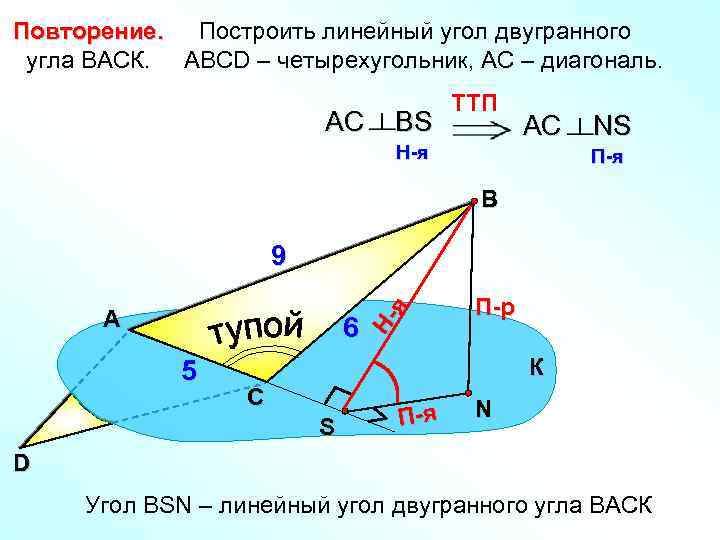Повторение. Построить линейный угол двугранного угла ВАСК. АВСD – четырехугольник, АС – диагональ. АС ВS TTП H-я АС NS П-я В А 6 5 Ня 9 П-р К С S П-я N D Угол ВSN – линейный угол двугранного угла ВАСК

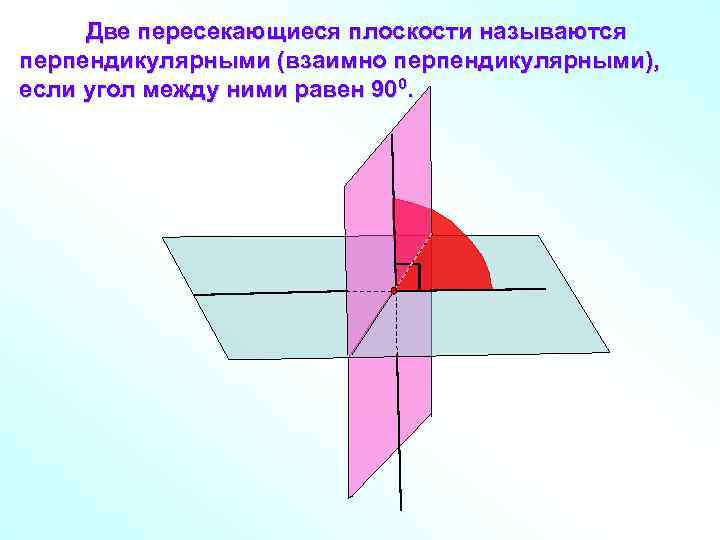Две пересекающиеся плоскости называются перпендикулярными (взаимно перпендикулярными), если угол между ними равен 900.

Примером взаимно перпендикулярных плоскостей служат плоскости стены и пола комнаты, плоскости стены и потолка.

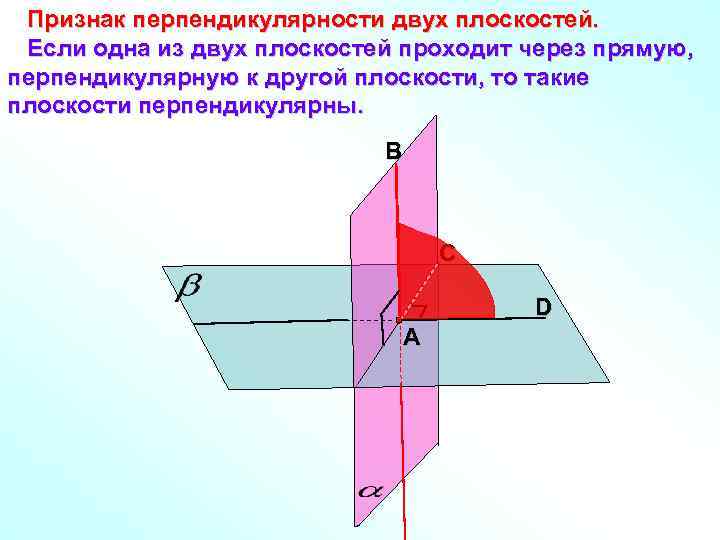Признак перпендикулярности двух плоскостей. Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны. В С D А

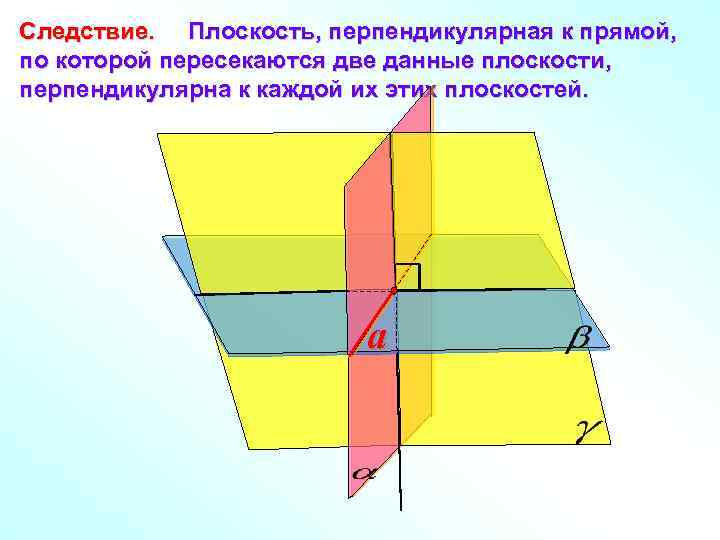Следствие. Плоскость, перпендикулярная к прямой, по которой пересекаются две данные плоскости, перпендикулярна к каждой их этих плоскостей. a

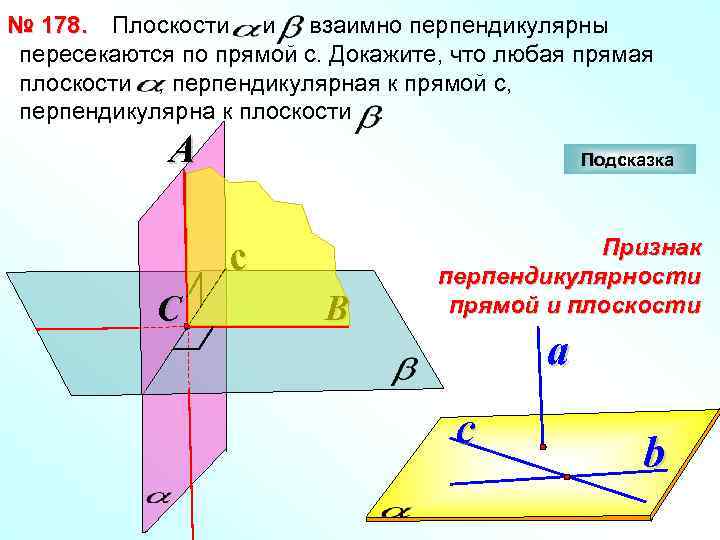№ 178. Плоскости и взаимно перпендикулярны пересекаются по прямой с. Докажите, что любая прямая плоскости , перпендикулярная к прямой с, перпендикулярна к плоскости. A Подсказка c C B Признак перпендикулярности прямой и плоскости a c b

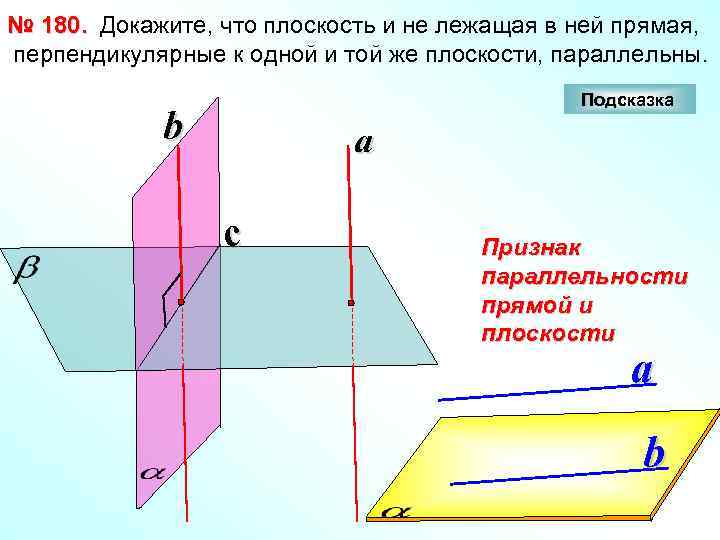№ 180. Докажите, что плоскость и не лежащая в ней прямая, перпендикулярные к одной и той же плоскости, параллельны. Подсказка b a c Признак параллельности прямой и плоскости a b

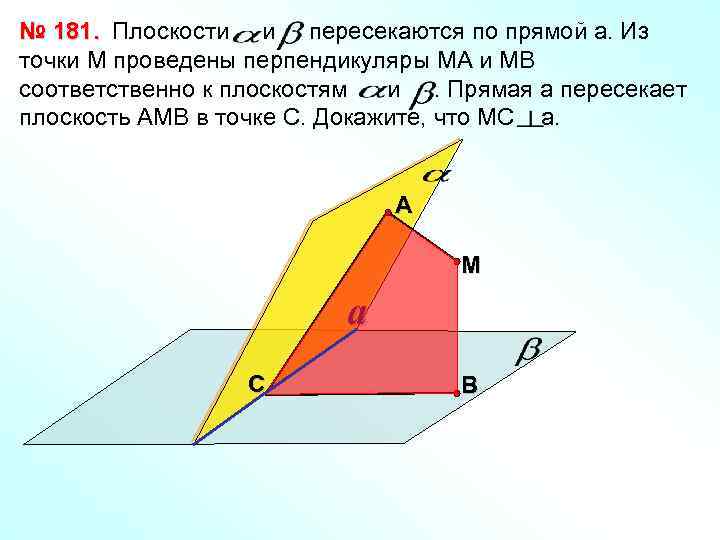№ 181. Плоскости и пересекаются по прямой а. Из точки М проведены перпендикуляры МА и МВ соответственно к плоскостям и. Прямая а пересекает плоскость АМВ в точке С. Докажите, что МС а. А М a С В

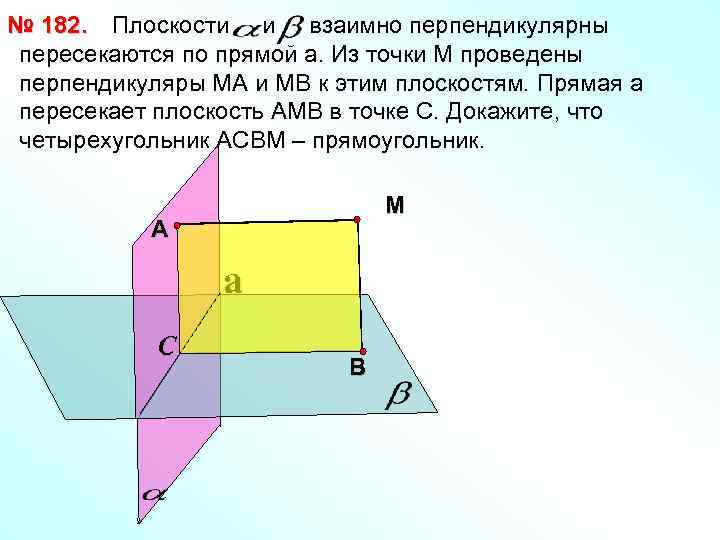№ 182. Плоскости и взаимно перпендикулярны пересекаются по прямой a. Из точки М проведены перпендикуляры МА и МВ к этим плоскостям. Прямая а пересекает плоскость АМВ в точке С. Докажите, что четырехугольник АСВМ – прямоугольник. М А a С В

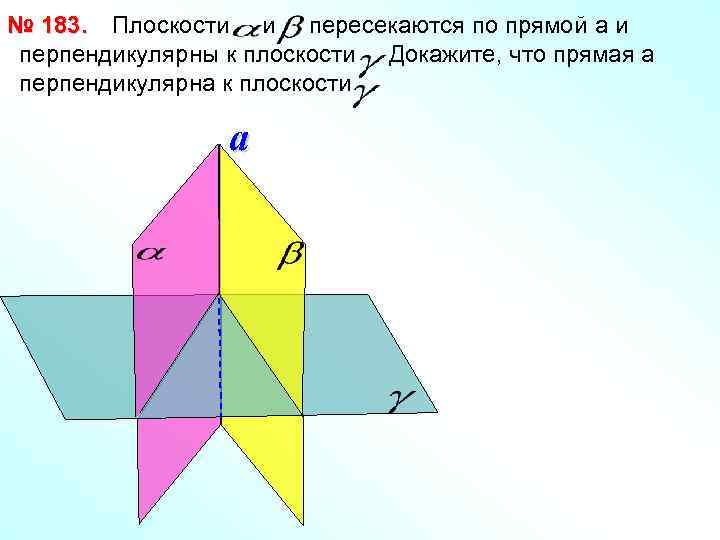№ 183. Плоскости и пересекаются по прямой a и перпендикулярны к плоскости. Докажите, что прямая а перпендикулярна к плоскости. a

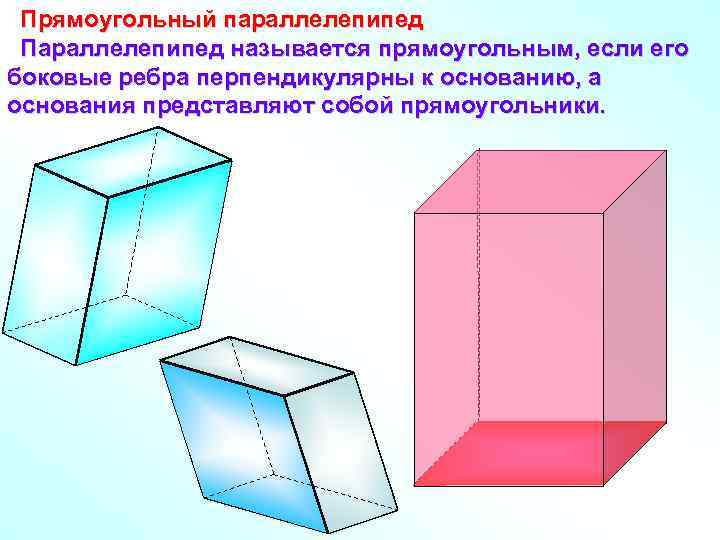Прямоугольный параллелепипед Параллелепипед называется прямоугольным, если его боковые ребра перпендикулярны к основанию, а основания представляют собой прямоугольники.

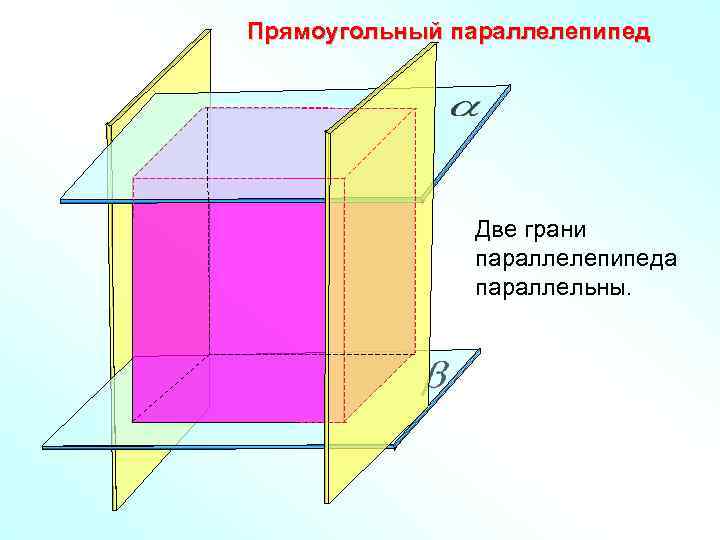Прямоугольный параллелепипед Две грани параллелепипеда параллельны.

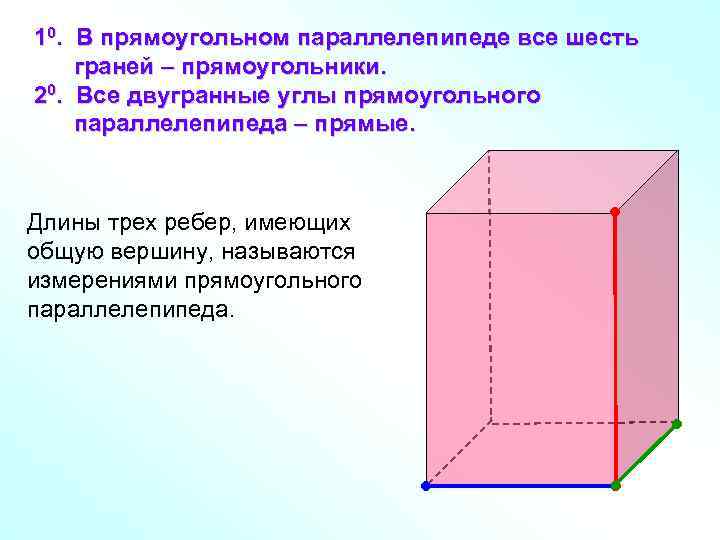10. В прямоугольном параллелепипеде все шесть граней – прямоугольники. 20. Все двугранные углы прямоугольного параллелепипеда – прямые. Длины трех ребер, имеющих общую вершину, называются измерениями прямоугольного параллелепипеда.

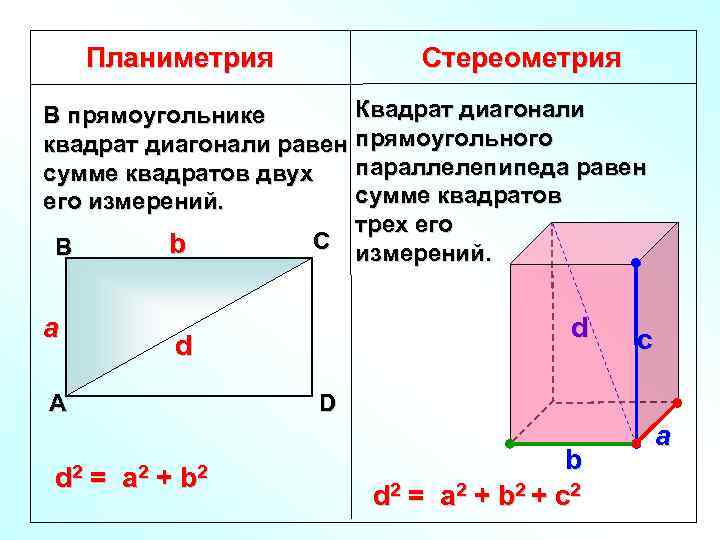Планиметрия Стереометрия Квадрат диагонали В прямоугольнике квадрат диагонали равен прямоугольного параллелепипеда равен сумме квадратов двух сумме квадратов его измерений. трех его С измерений. b В a d А d 2 d с D = a 2 + b 2 b d 2 = a 2 + b 2 + с 2 a

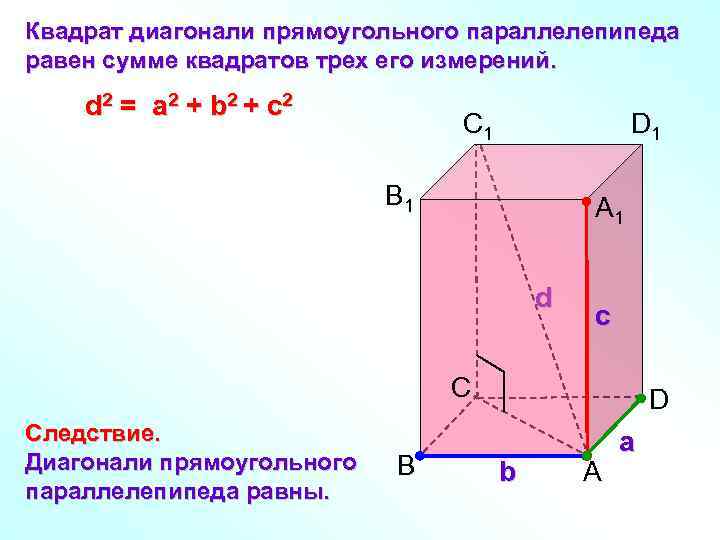Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений. d 2 = a 2 + b 2 + с 2 C 1 D 1 B 1 A 1 d с C Следствие. Диагонали прямоугольного параллелепипеда равны. B D b A а

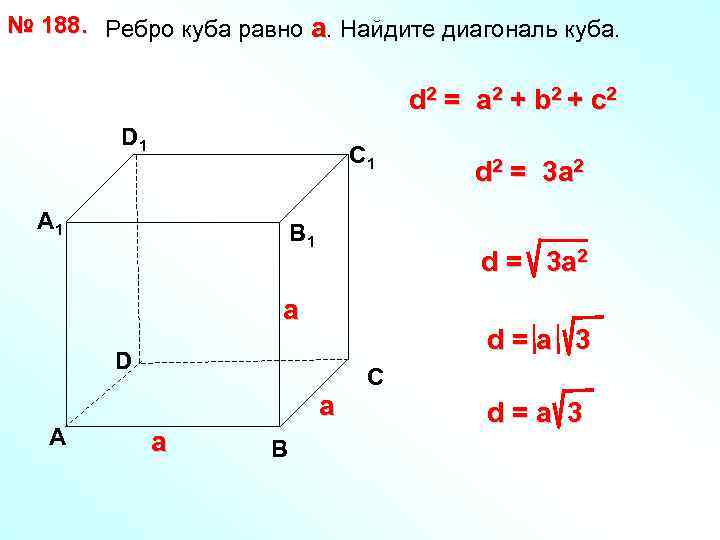№ 188. Ребро куба равно а. Найдите диагональ куба. d 2 = a 2 + b 2 + с 2 D 1 С 1 А 1 В 1 d = 3 a 2 а d=a 3 D а А а В d 2 = 3 a 2 С d=a 3

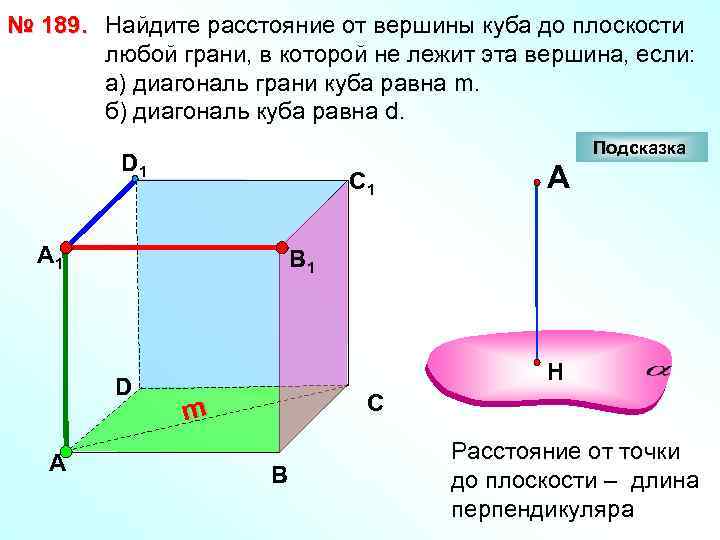№ 189. Найдите расстояние от вершины куба до плоскости любой грани, в которой не лежит эта вершина, если: а) диагональ грани куба равна m. б) диагональ куба равна d. Подсказка D 1 С 1 А 1 В 1 D А А Н С m В Расстояние от точки до плоскости – длина перпендикуляра

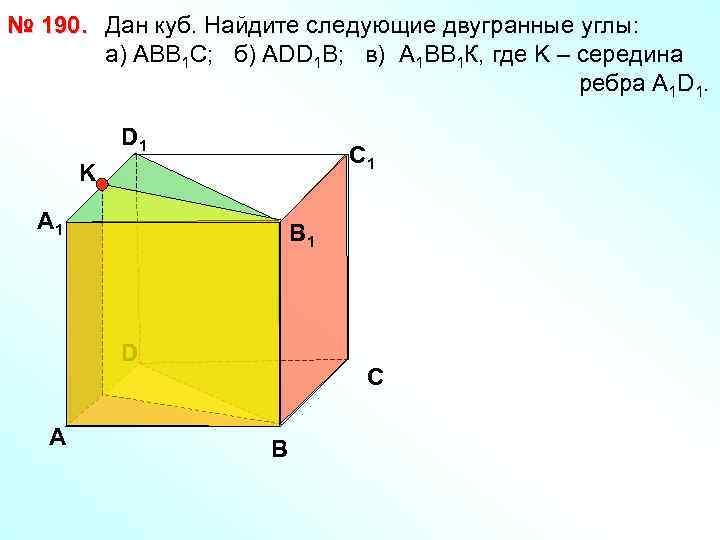№ 190. Дан куб. Найдите следующие двугранные углы: a) АВВ 1 С; б) АDD 1 B; в) А 1 ВВ 1 К, где K – середина ребра А 1 D 1. D 1 С 1 K А 1 В 1 D А С В

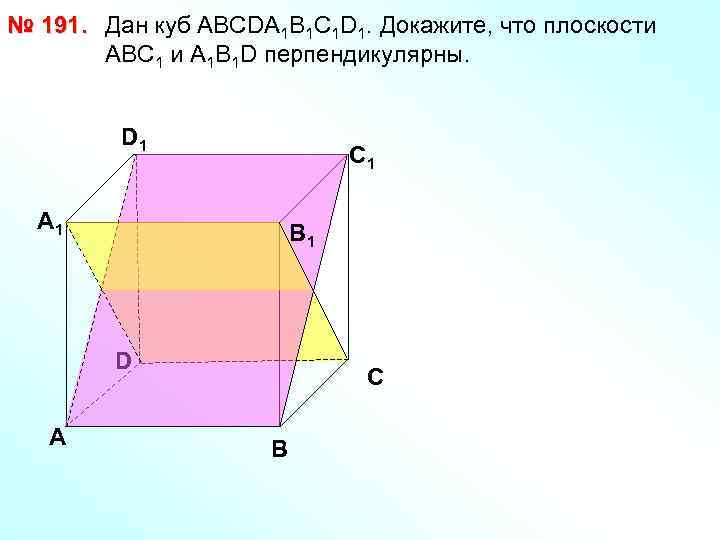№ 191. Дан куб АВСDА 1 В 1 С 1 D 1. Докажите, что плоскости АВС 1 и А 1 В 1 D перпендикулярны. D 1 С 1 А 1 В 1 D А С В

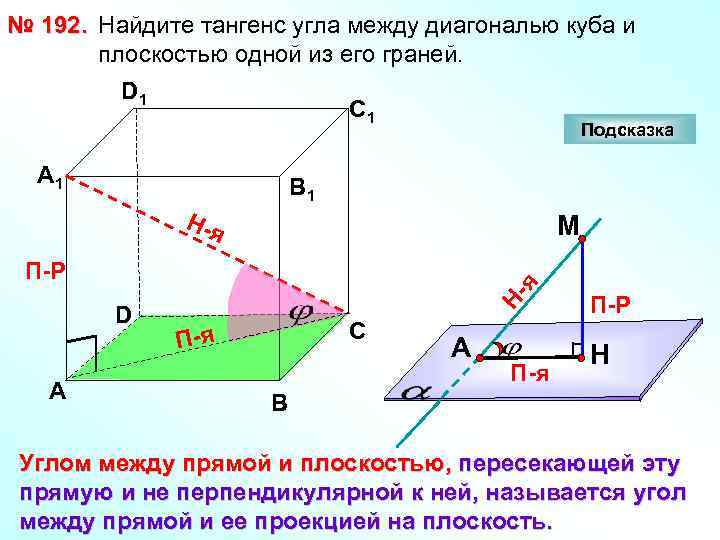№ 192. Найдите тангенс угла между диагональю куба и плоскостью одной из его граней. D 1 С 1 А 1 Подсказка В 1 Н-я М D А Н- я П-Р С П-я А П-я П-Р Н В Углом между прямой и плоскостью, пересекающей эту прямую и не перпендикулярной к ней, называется угол между прямой и ее проекцией на плоскость.

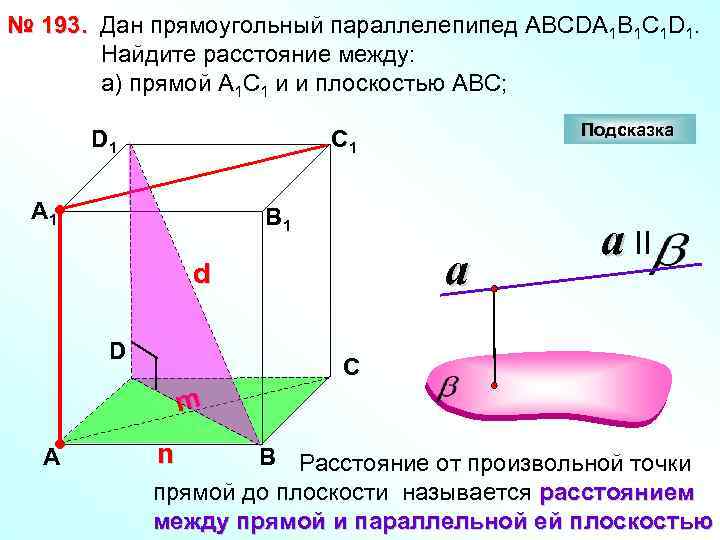№ 193. Дан прямоугольный параллелепипед АВСDА 1 В 1 С 1 D 1. Найдите расстояние между: а) прямой А 1 С 1 и и плоскостью АВС; D 1 Подсказка С 1 А 1 В 1 a d D a II С m А n В Расстояние от произвольной точки прямой до плоскости называется расстоянием между прямой и параллельной ей плоскостью

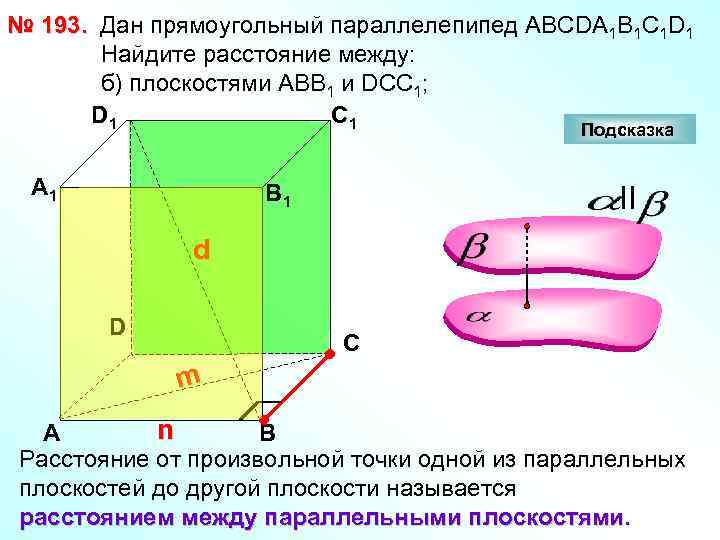№ 193. Дан прямоугольный параллелепипед АВСDА 1 В 1 С 1 D 1 Найдите расстояние между: б) плоскостями АВВ 1 и DCC 1; D 1 С 1 Подсказка А 1 В 1 II d D С m n А В Расстояние от произвольной точки одной из параллельных плоскостей до другой плоскости называется расстоянием между параллельными плоскостями.

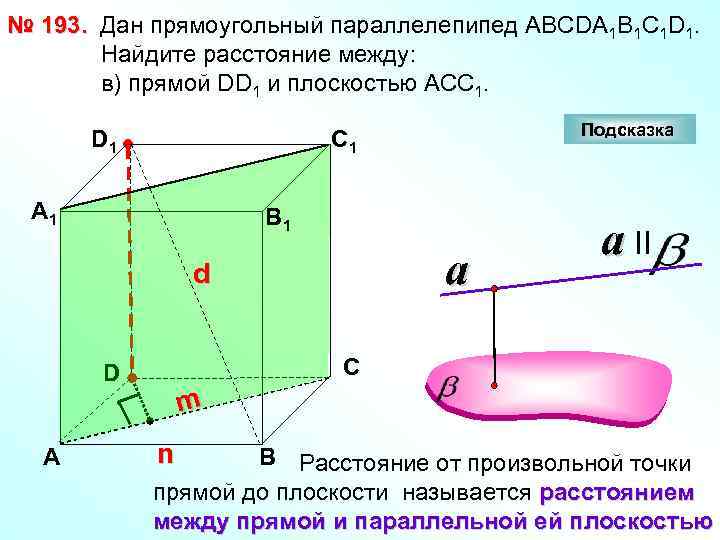№ 193. Дан прямоугольный параллелепипед АВСDА 1 В 1 С 1 D 1. Найдите расстояние между: в) прямой DD 1 и плоскостью АСС 1. D 1 Подсказка С 1 А 1 В 1 a d a II С D m А n В Расстояние от произвольной точки прямой до плоскости называется расстоянием между прямой и параллельной ей плоскостью

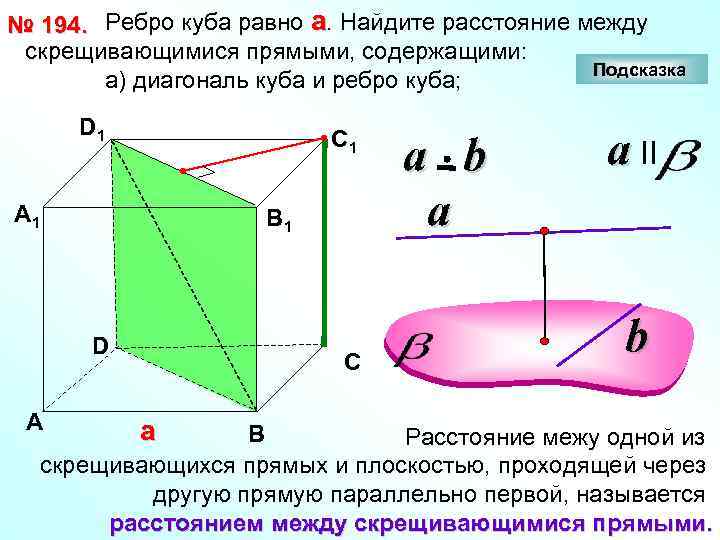№ 194. Ребро куба равно а. Найдите расстояние между скрещивающимися прямыми, содержащими: Подсказка а) диагональ куба и ребро куба; D 1 С 1 А 1 В 1 D А С а a b a a II b В Расстояние межу одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой, называется расстоянием между скрещивающимися прямыми.

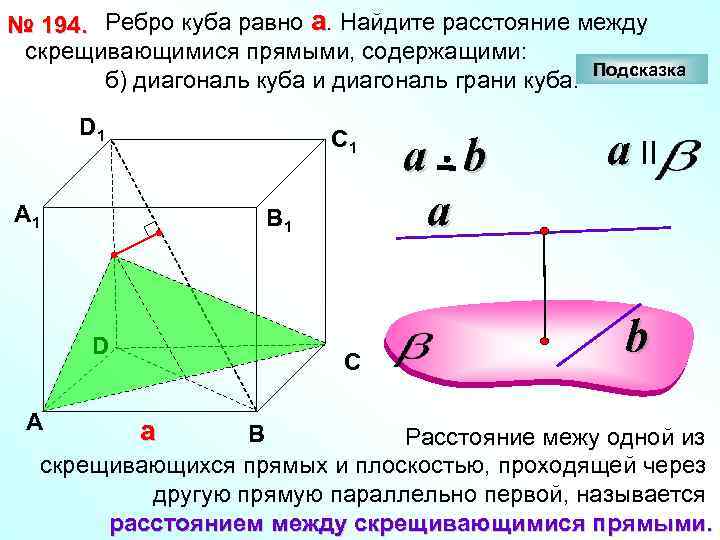№ 194. Ребро куба равно а. Найдите расстояние между скрещивающимися прямыми, содержащими: Подсказка б) диагональ куба и диагональ грани куба. D 1 С 1 А 1 В 1 D А С а a b a a II b В Расстояние межу одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой, называется расстоянием между скрещивающимися прямыми.

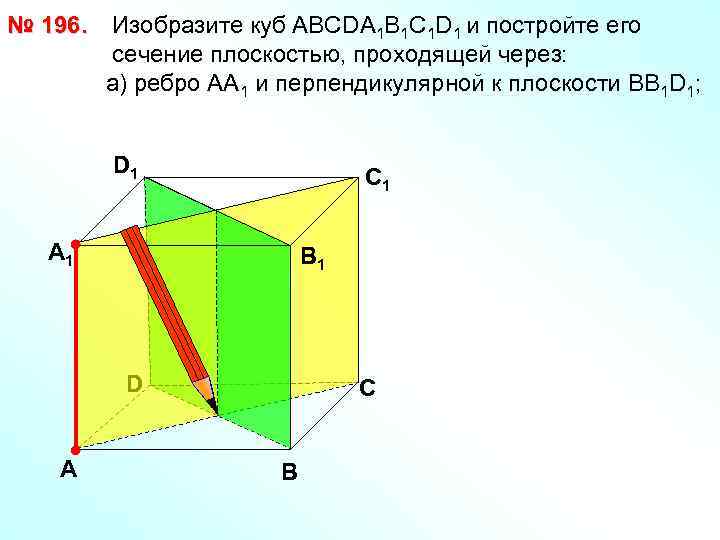№ 196. Изобразите куб АВСDА 1 В 1 С 1 D 1 и постройте его сечение плоскостью, проходящей через: а) ребро АА 1 и перпендикулярной к плоскости ВВ 1 D 1; D 1 С 1 А 1 В 1 D А С В

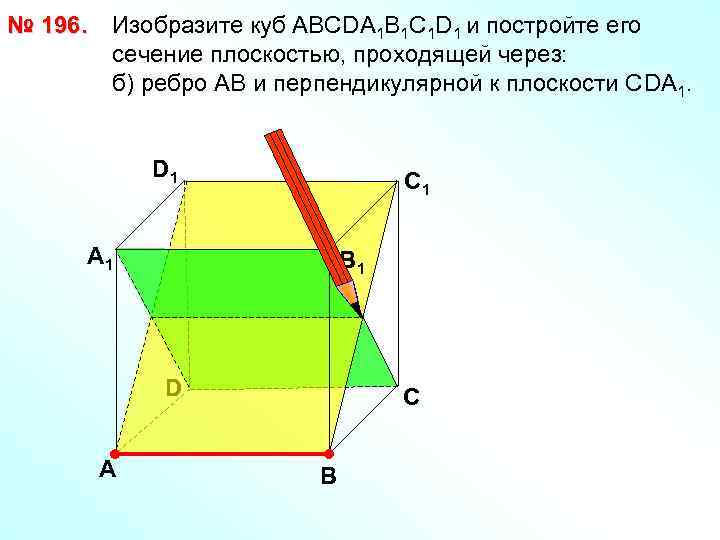№ 196. Изобразите куб АВСDА 1 В 1 С 1 D 1 и постройте его сечение плоскостью, проходящей через: б) ребро АВ и перпендикулярной к плоскости СDA 1. D 1 С 1 А 1 В 1 D А С В

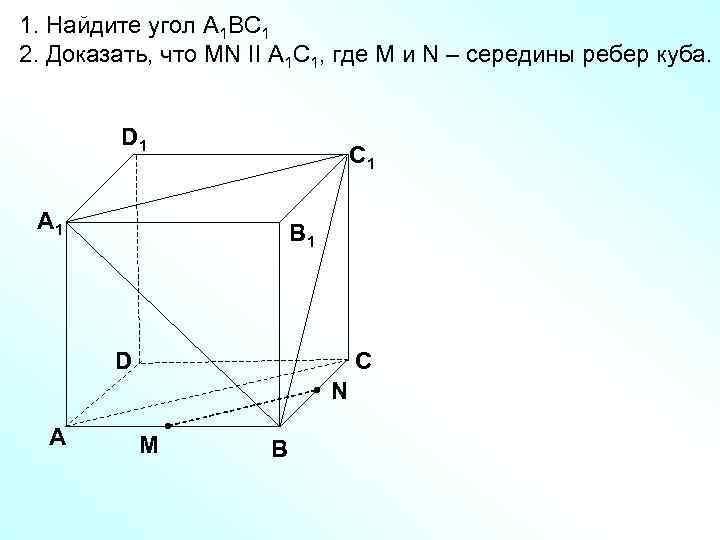1. Найдите угол А 1 ВС 1 2. Доказать, что MN II А 1 С 1, где M и N – середины ребер куба. D 1 С 1 А 1 В 1 D С N А M В

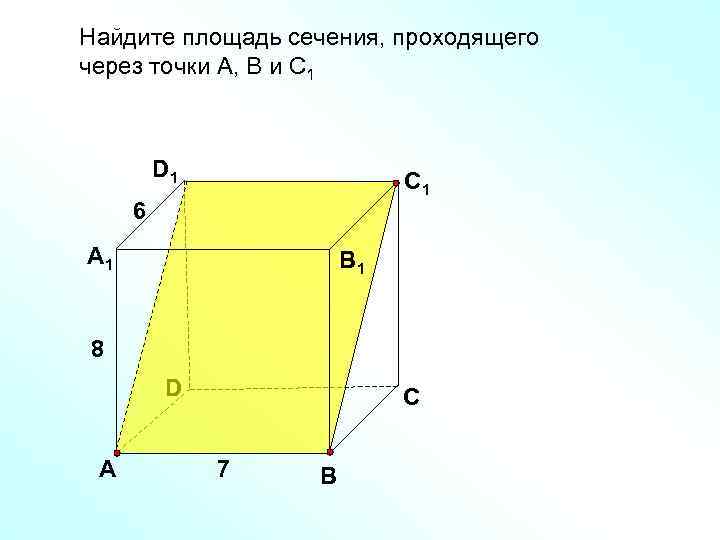Найдите площадь сечения, проходящего через точки А, В и С 1 D 1 С 1 6 А 1 В 1 8 D А С 7 В