Повторение по теме Числовые функции Свойства функции 10

Повторение по теме: Числовые функции. Свойства функции. 10 класс

Определение функции. Обозначение функции. у( х ) - функция х - аргумент зависимая переменная независимая переменная

1. Числовая функция. Правила сопоставления 1. Описание 2. Таблица 3. График 4. Формула

Область определения функции. Область определения функции у(х) это все значения аргумента - Х D(у)- область определения функции

Область значений функции. Область значений функции у(х) это все значения - У _ Е(у) - область значений функции

Свойства функции. Область определения- D(х) Все значения которые принимает независимая переменная -аргумент(х) Область значения – E(у) Все допустимые значения которые принимает зависимая переменная функция(у) Промежутки возрастания и убывания f(х) – возрастает, если наибольшему значению аргумента (х ) соответствует наибольшее значение функции (f(х)) f(х) – убывает, если наибольшему значению аргумента (х ) соответствует наименьшее значение функции (f(х)) Промежутки знакопостоянства Все значения аргумента (х) при которых функция принимает положительные значения (у >0) или отрицательные значения( у <0) Нули функции Значения аргумента(х), при котором значение функции равно нулю( у = 0). Четность и f(х) – четная, если f(-х) = f(х), график четной функции нечетность функции симметричен оси ОУ f(х) – четная, если f(-х) = - f(х), график нечетной функции симметричен начала координат Наибольшее и наименьшее значение функции Наибольшее значение функции – это число M= f(х0), такое что f(х) ≤ f(х0) Наименьшее значение функции - это число m= f(х0), такое что f(х) ≥ f(х0)

Свойства функций Монотонность • Определение Функцию y=f(x) называют возрастающей на множестве Х c D(f), если для любых двух точек х₁ и х₂ множества Х, таких, что х₁<х₂ выполняется неравенство f(х₁) < f(х₂).

2. Возрастание и убывание функций. Определение 2. Функция f возрастает на промежутке P если x 1є P и x 2 є P из того что x 2 > x 1 следует f(x 2 )>f(x 1) (или из того что x 2 < x 1 следует f(x 2 ) x 1 следует f(x 2 )f(x 1) ).

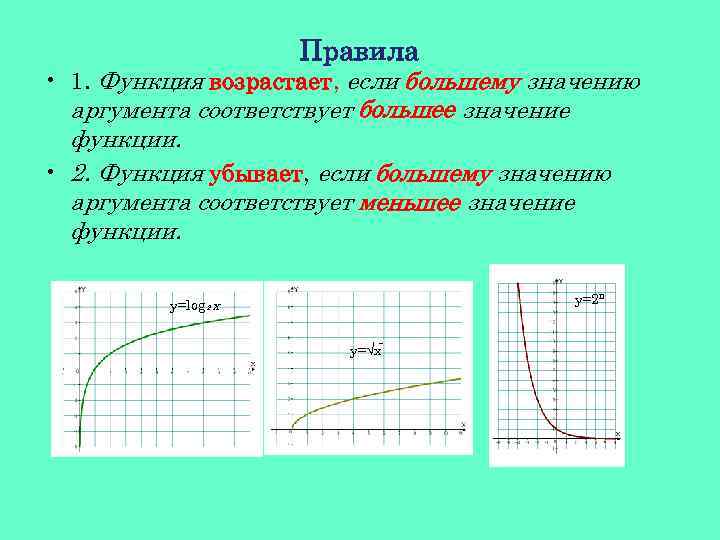Правила • 1. Функция возрастает, если большему значению аргумента соответствует большее значение функции. • 2. Функция убывает, если большему значению аргумента соответствует меньшее значение функции. у=2ⁿ y=log₂х ⁻ у=√х

3. Экстремумы. Определение 4. Точка x 0 называется точкой минимума функции f, если для всех x из некоторой окрестности x 0 выполнено неравенство f(x)≥f(x 0). Определение 5. Точка x 0 называется точкой максимума функции f, если для всех x из некоторой окрестности x 0 выполнено неравенство f(x) ≤f(x 0).

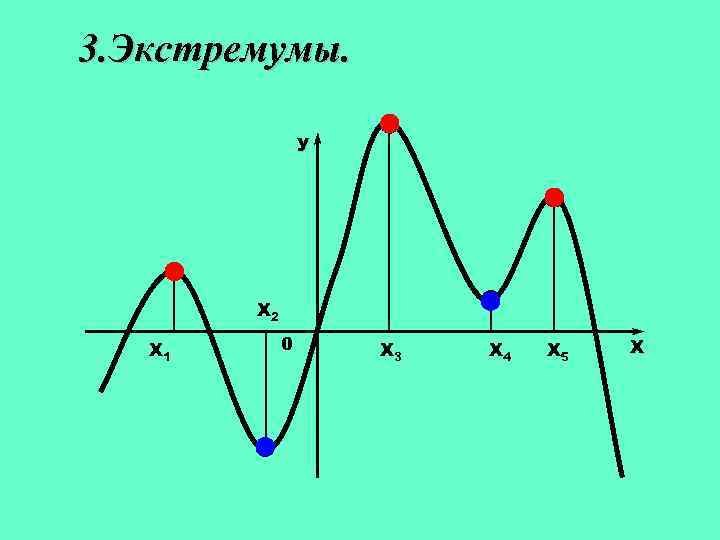3. Экстремумы. У Х 2 Х 1 0 Х 3 Х 4 Х 5 Х

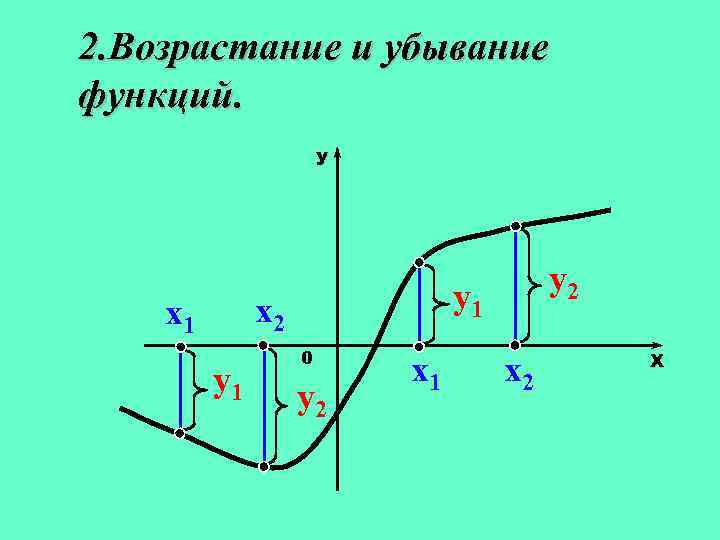2. Возрастание и убывание функций. У y 1 x 2 x 1 y 2 0 y 2 x 1 x 2 Х

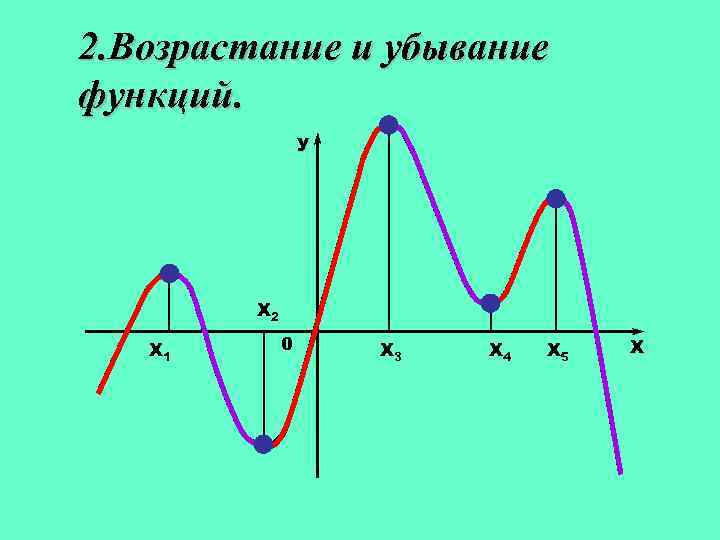2. Возрастание и убывание функций. У Х 2 Х 1 0 Х 3 Х 4 Х 5 Х

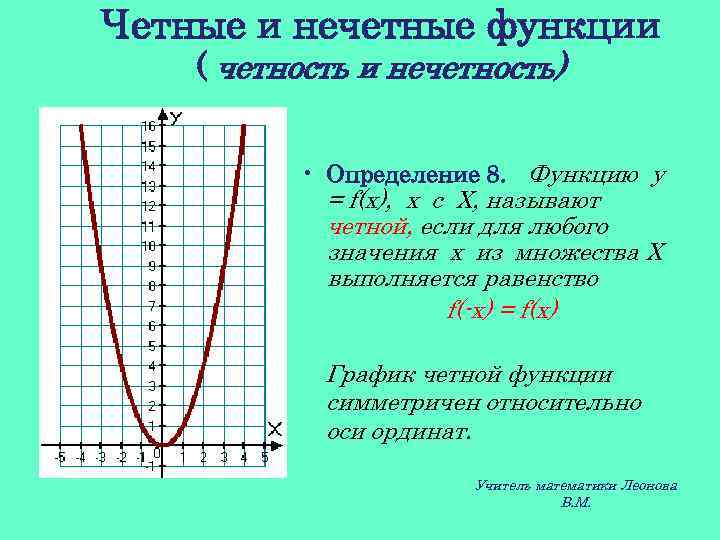Четные и нечетные функции ( четность и нечетность) • Определение 8. Функцию y = f(x), х с Х, называют четной, если для любого значения х из множества Х выполняется равенство f(-x) = f(x) График четной функции симметричен относительно оси ординат. Учитель математики Леонова В. М.

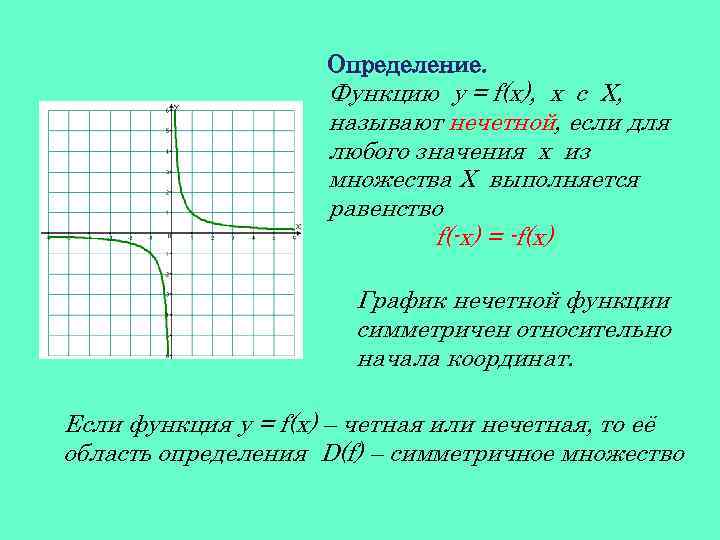Определение. Функцию y = f(x), х с Х, называют нечетной, если для любого значения х из множества Х выполняется равенство f(-x) = -f(x) График нечетной функции симметричен относительно начала координат. Если функция y = f(x) – четная или нечетная, то её область определения D(f) – симметричное множество

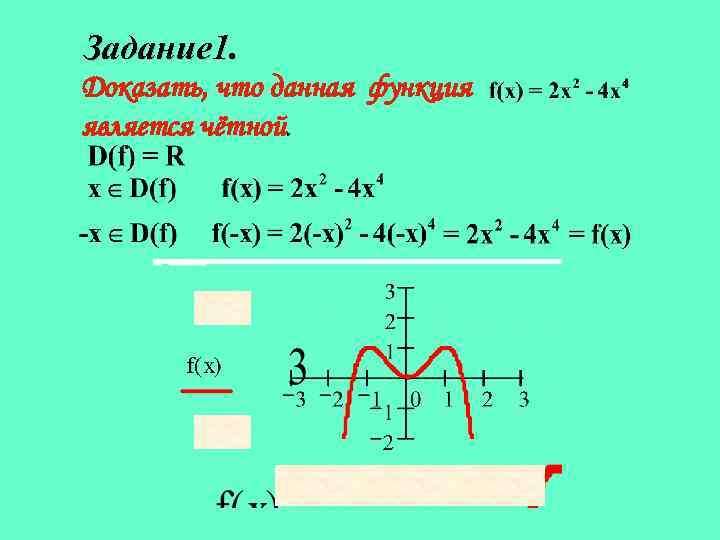Задание 1. Доказать, что данная функция является чётной.

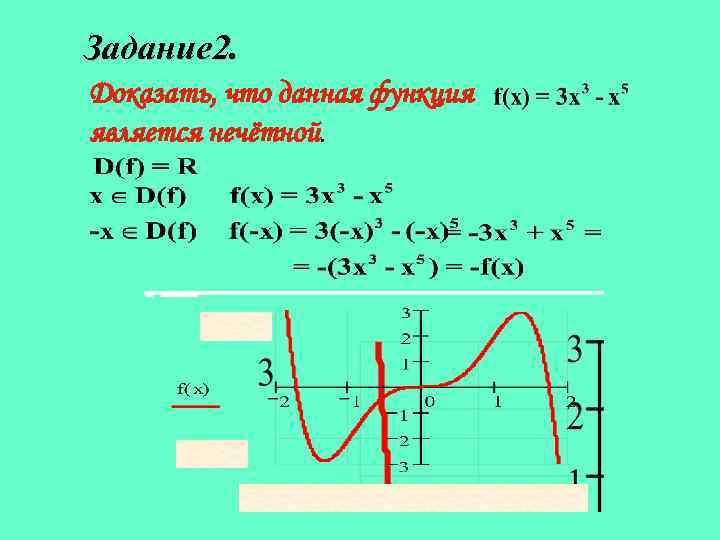Задание 2. Доказать, что данная функция является нечётной.

Задание 5. Исследовать функцию нечётность. Функция нечетная функция на чётность, является ни четная ни

Задание 6. Исследовать функцию чётность, нечётность. Функция нечетная функция на является ни четная ни

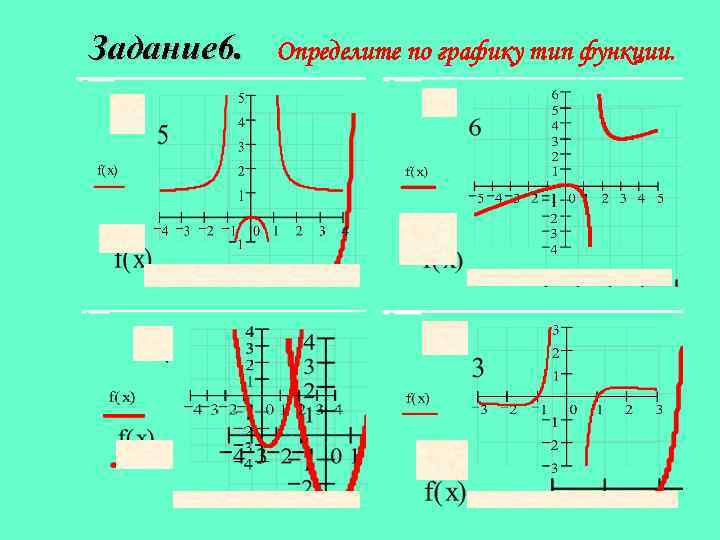Задание 6. Определите по графику тип функции.

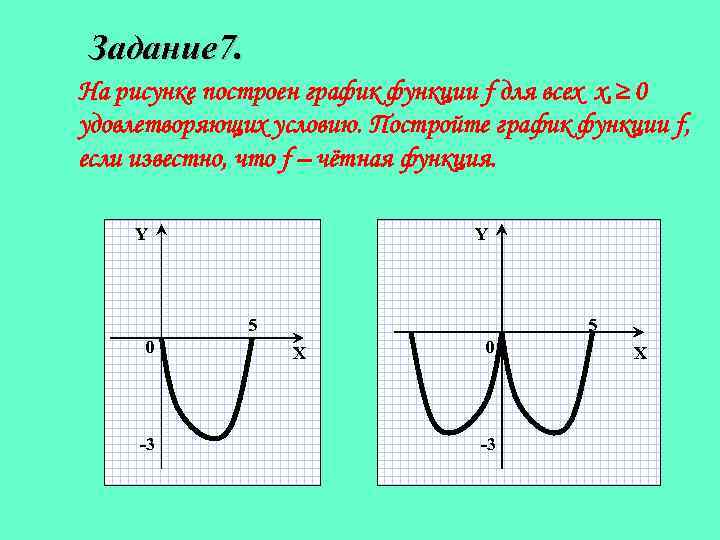Задание 7. На рисунке построен график функции f для всех x, ≥ 0 удовлетворяющих условию. Постройте график функции f, если известно, что f – чётная функция. Y Y 5 0 -3 5 X 0 -3 X

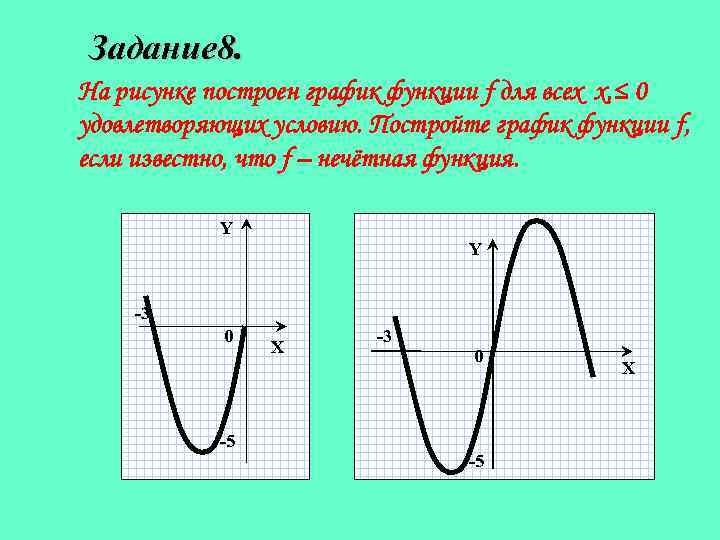Задание 8. На рисунке построен график функции f для всех x, ≤ 0 удовлетворяющих условию. Постройте график функции f, если известно, что f – нечётная функция. Y Y -3 0 X -3 0 -5 -5 X

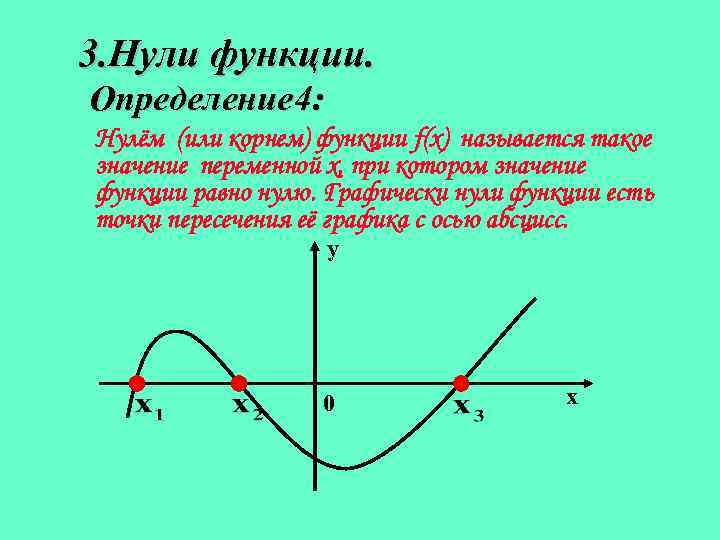3. Нули функции. Определение 4: Нулём (или корнем) функции f(x) называется такое значение переменной х, при котором значение функции равно нулю. Графически нули функции есть точки пересечения её графика с осью абсцисс. у 0 х

График функции (х; у)- координаты точки в плоскости у – ордината точки х – абсцисса точки (координата оси ОУ) х )- функция ОХ) х - аргумент у(

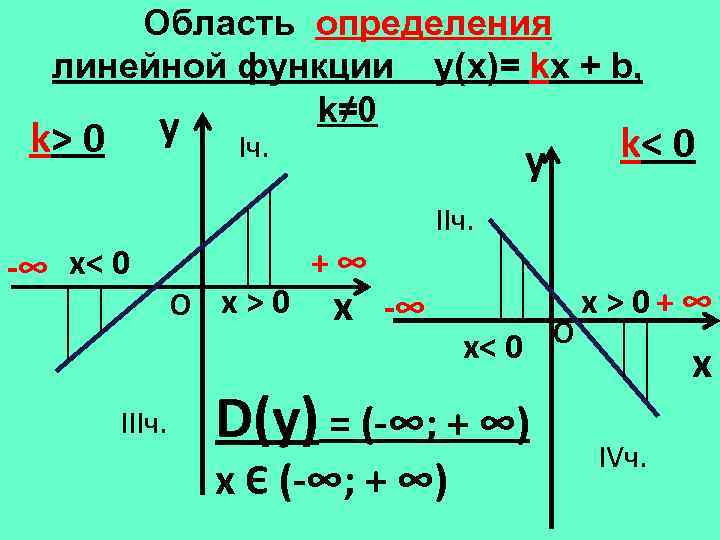Область определения линейной функции y(х)= kx + b, k≠ 0 y k> 0 Iч. y k< 0 IIч. -∞ х< 0 IIIч. О х>0 +∞ x -∞ О х< 0 D(у) = (-∞; + ∞) х Є (-∞; + ∞) х > 0+ ∞ x IVч.

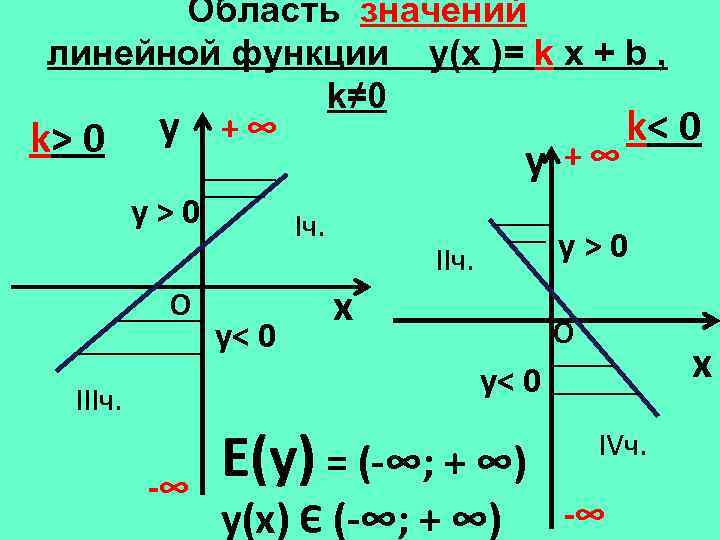Область значений линейной функции y(х )= k x + b , k≠ 0 k< 0 k> 0 y + ∞ y +∞ у>0 О Iч. у< 0 у>0 IIч. x О x у< 0 IIIч. -∞ Е(у) = (-∞; + ∞) у(х) Є (-∞; + ∞) IVч. -∞

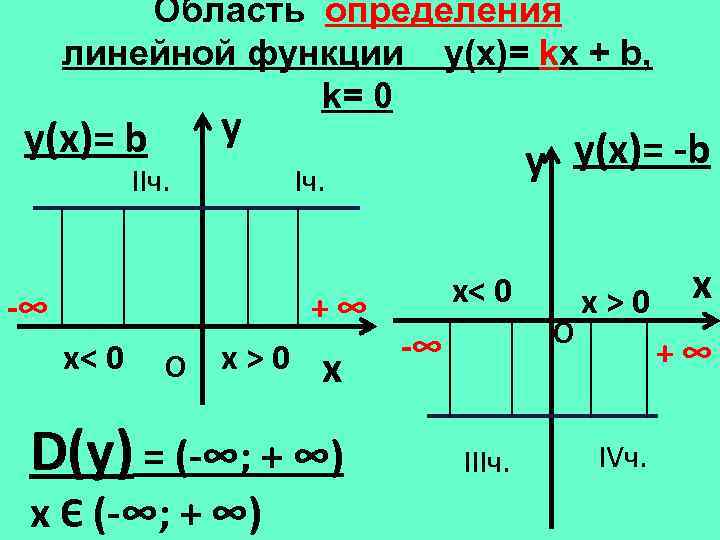Область определения линейной функции y(х)= kx + b, k= 0 y(х)= b y IIч. -∞ Iч. +∞ х< 0 О х>0 x D(у) = (-∞; + ∞) х Є (-∞; + ∞) y y(х)= -b х< 0 О -∞ IIIч. x х>0 +∞ IVч.

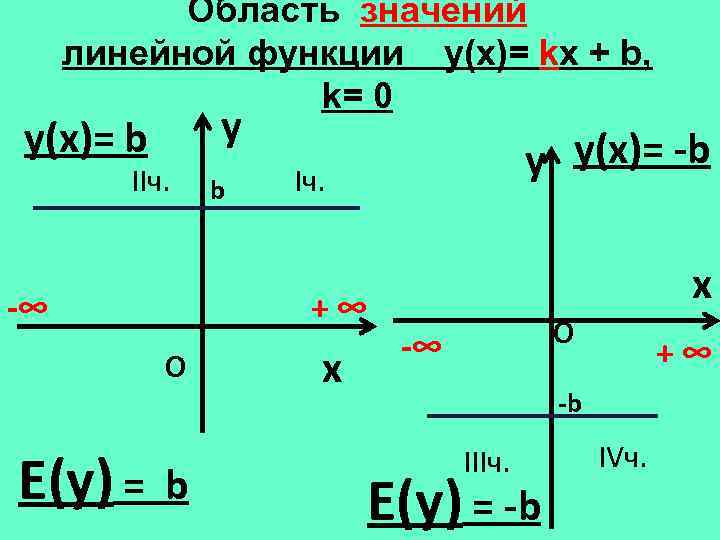Область значений линейной функции y(х)= kx + b, k= 0 y y(х)= b IIч. -∞ Iч. +∞ О Е(у) = b b y y(х)= -b x x О -∞ +∞ -b IIIч. Е(у) = -b IVч.

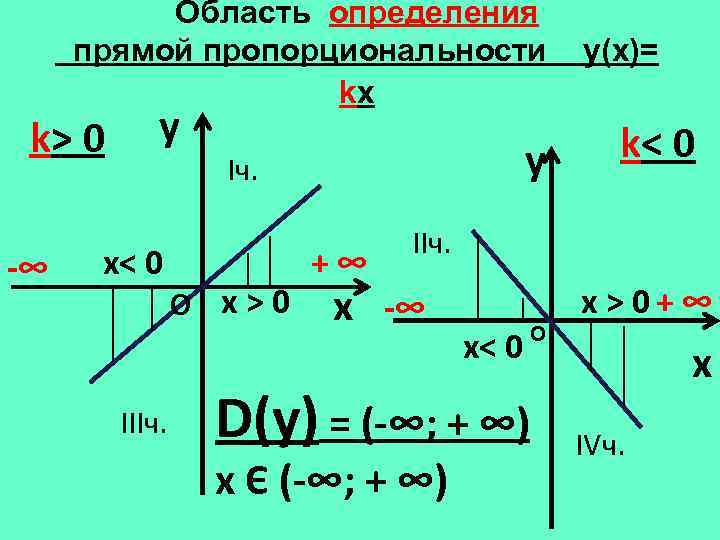Область определения прямой пропорциональности kx k> 0 -∞ y х< 0 IIIч. y Iч. О х>0 +∞ y(х)= k< 0 IIч. x -∞ х< 0 D(у) = (-∞; + ∞) х Є (-∞; + ∞) О х > 0+ ∞ x IVч.

k> 0 Область значений прямой пропорциональности y(х )= k x +∞ y y +∞ Iч. у>0 IIIч. О IIч. у< 0 у>0 x О x у< 0 -∞ k< 0 Е(у) = (-∞; + ∞) у(х) Є (-∞; + ∞) IVч. -∞

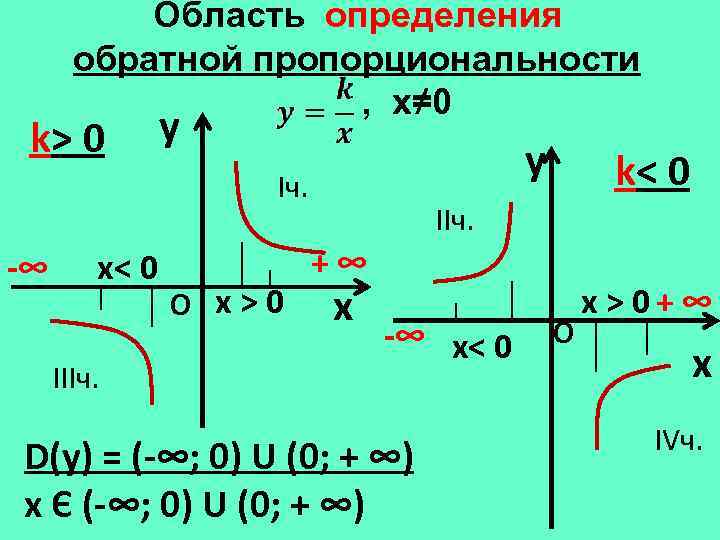Область определения обратной пропорциональности , х≠ 0 k> 0 y y Iч. -∞ х< 0 IIIч. О х>0 k< 0 IIч. +∞ x -∞ х< 0 D(у) = (-∞; 0) U (0; + ∞) х Є (-∞; 0) U (0; + ∞) О х > 0+ ∞ x IVч.

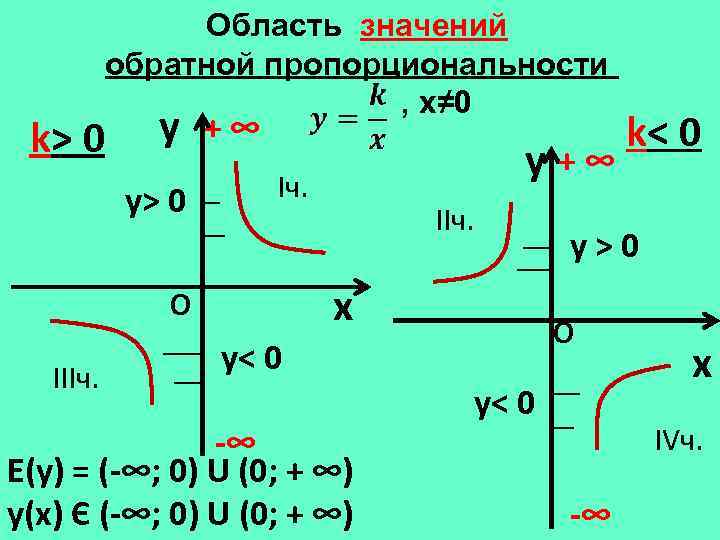Область значений обратной пропорциональности , х≠ 0 k> 0 y +∞ y> 0 Iч. IIч. y>0 x О IIIч. y +∞ О y< 0 -∞ Е(у) = (-∞; 0) U (0; + ∞) у(х) Є (-∞; 0) U (0; + ∞) k< 0 y< 0 x IVч. -∞

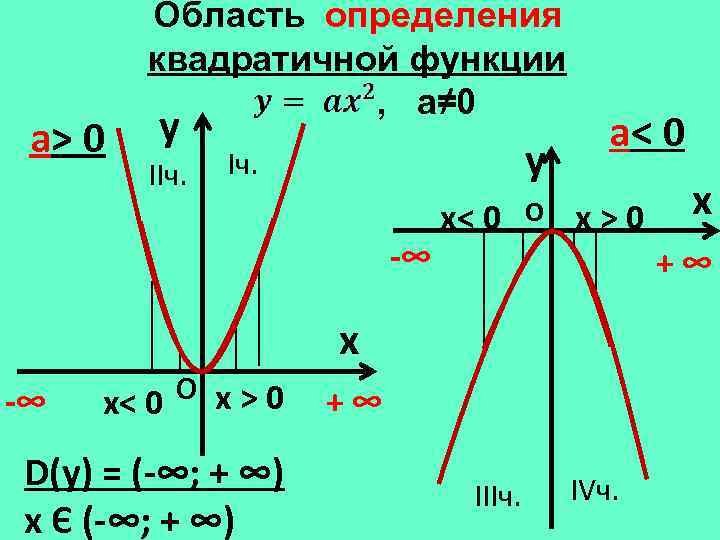а> 0 Область определения квадратичной функции , а≠ 0 y IIч. y Iч. -∞ х< 0 О а< 0 х>0 +∞ x -∞ О х>0 х< 0 D(у) = (-∞; + ∞) х Є (-∞; + ∞) x +∞ IIIч. IVч.

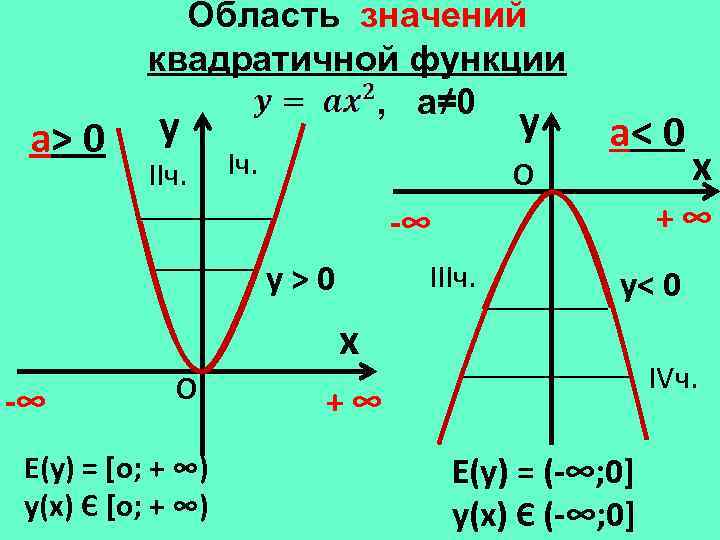а> 0 Область значений квадратичной функции , а≠ 0 y IIч. y Iч. О а< 0 +∞ -∞ у>0 IIIч. y< 0 x -∞ О Е(у) = [о; + ∞) у(х) Є [о; + ∞) x IVч. +∞ Е(у) = (-∞; 0] у(х) Є (-∞; 0]

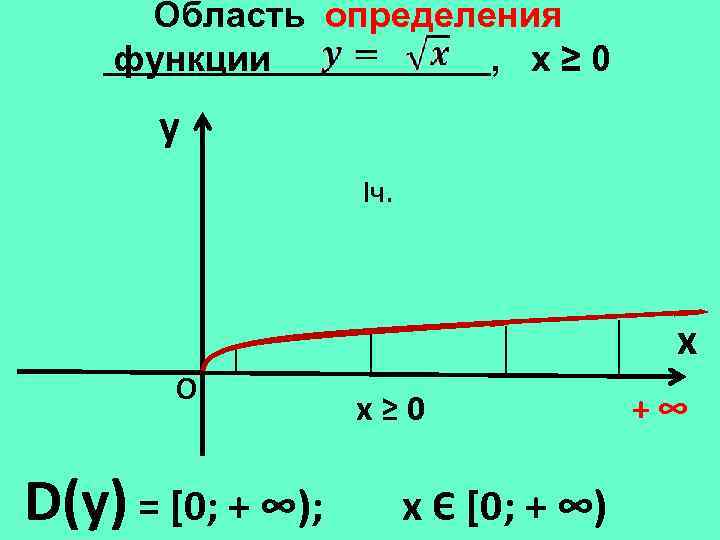Область определения функции , х≥ 0 y Iч. x О D(у) = [0; + ∞); х≥ 0 х Є [0; + ∞) +∞

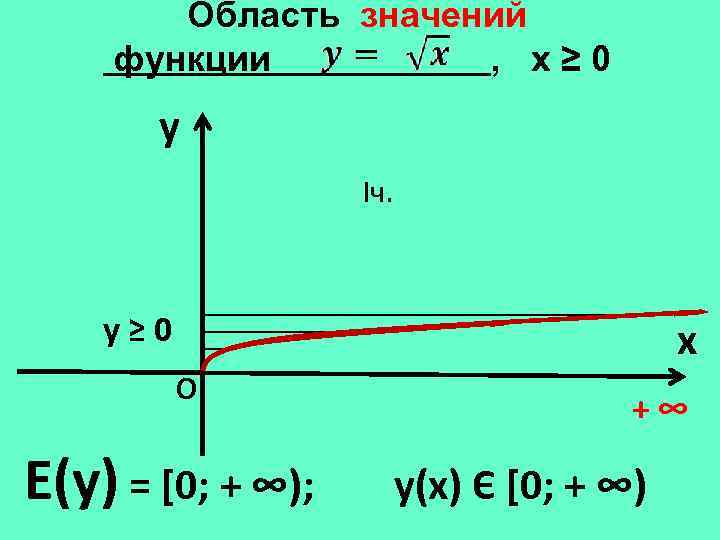Область значений функции , х≥ 0 y Iч. у≥ 0 x О Е(у) = [0; + ∞); +∞ у(х) Є [0; + ∞)

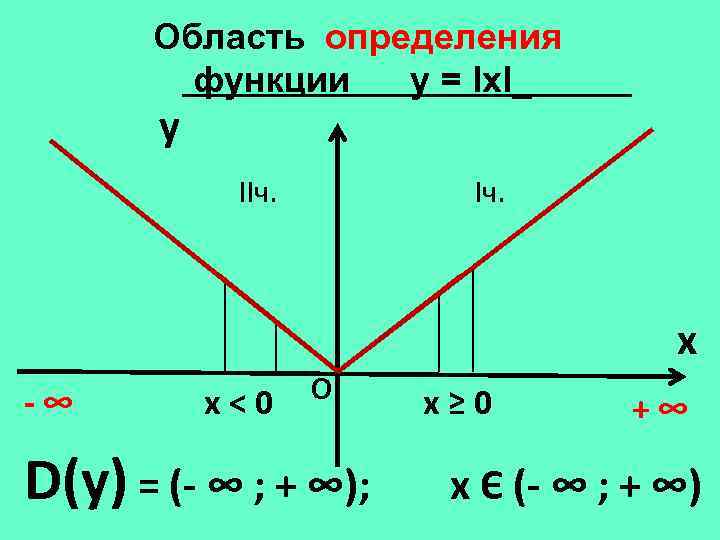Область определения функции у = lхl_ y IIч. x -∞ х<0 О D(у) = (- ∞ ; + ∞); х≥ 0 +∞ х Є (- ∞ ; + ∞)

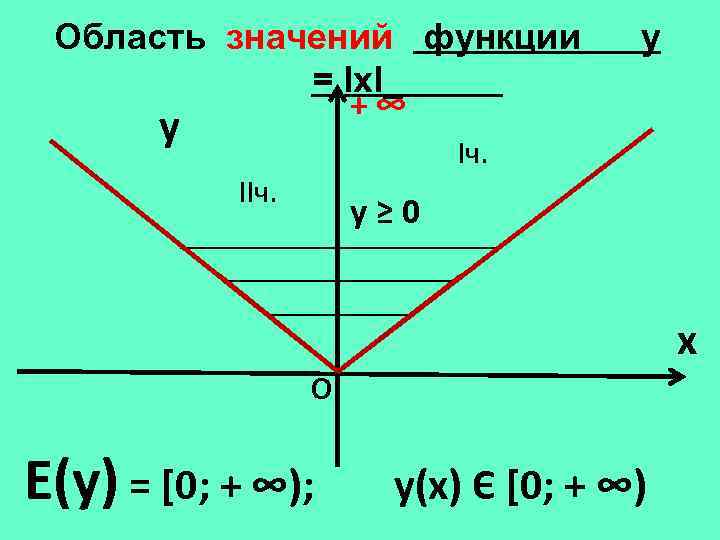Область значений функции = lхl_ +∞ y у Iч. IIч. у≥ 0 x О Е(у) = [0; + ∞); у(х) Є [0; + ∞)

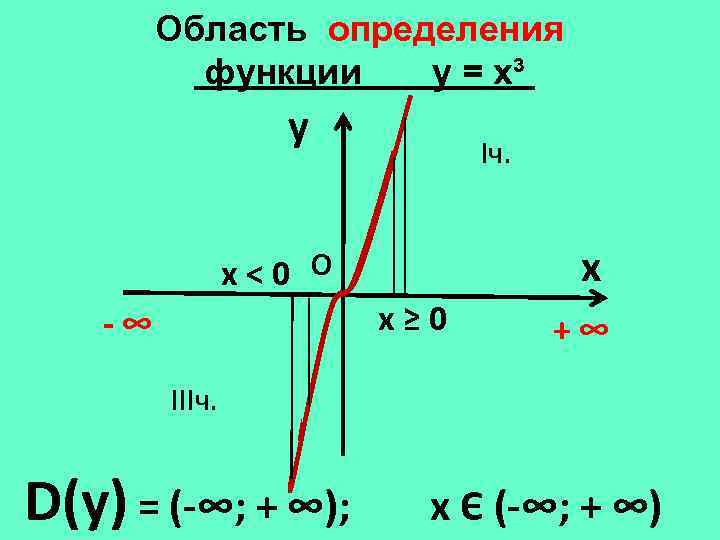Область определения функции у = х³ y Iч. x х<0 О х≥ 0 -∞ +∞ IIIч. D(у) = (-∞; + ∞); х Є (-∞; + ∞)

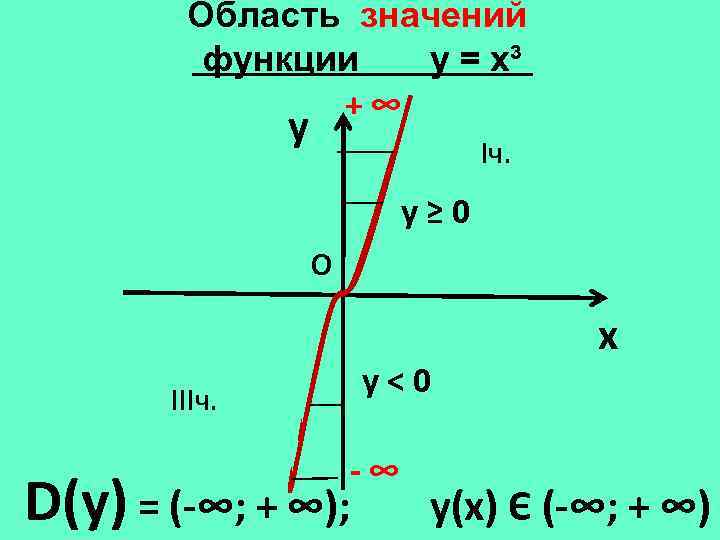Область значений функции у = х³ +∞ y Iч. у≥ 0 О IIIч. D(у) = (-∞; + ∞); у<0 -∞ x у(х) Є (-∞; + ∞)

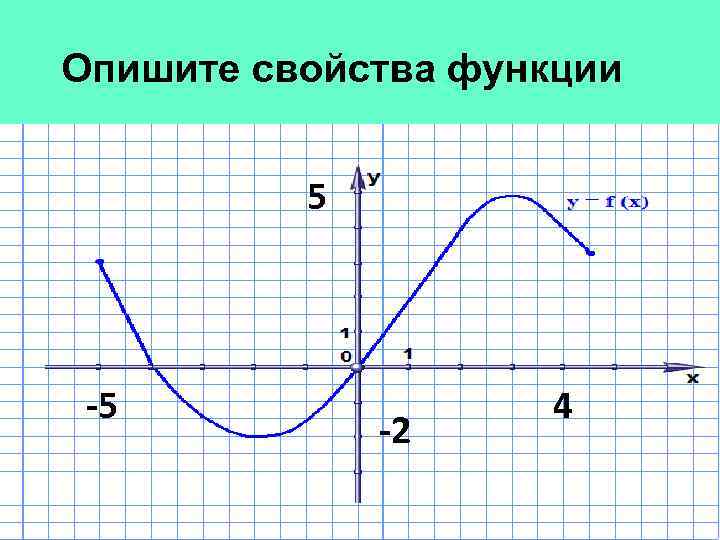Опишите свойства функции 5 -5 -2 4

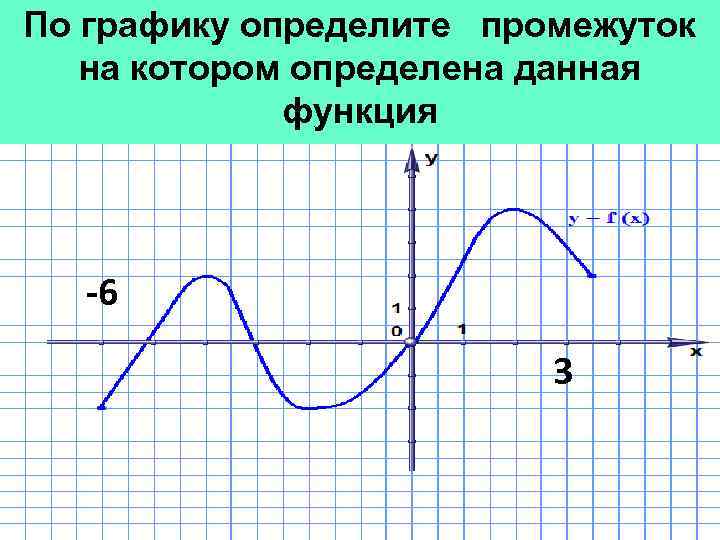По графику определите промежуток на котором определена данная функция -6 3

По графику определите промежуток на котором определена данная функция 4 -2 Е(у)= [-2; 4]

Найдите по графику область определения функции -5 D(у)= [-5; 5] 5

Найдите по графику область определения функции 6 -2 Е(у)= [-2; 6]

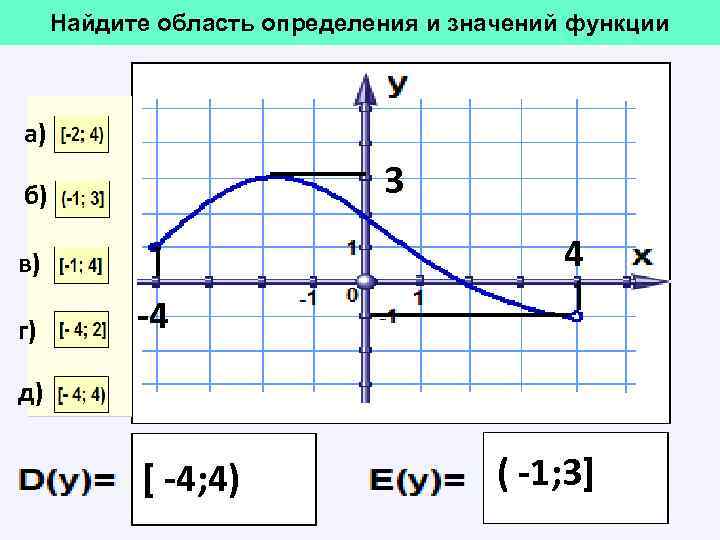Найдите область определения и значений функции а) 3 б) 4 в) г) -4 д) [ -4; 4) ( -1; 3]

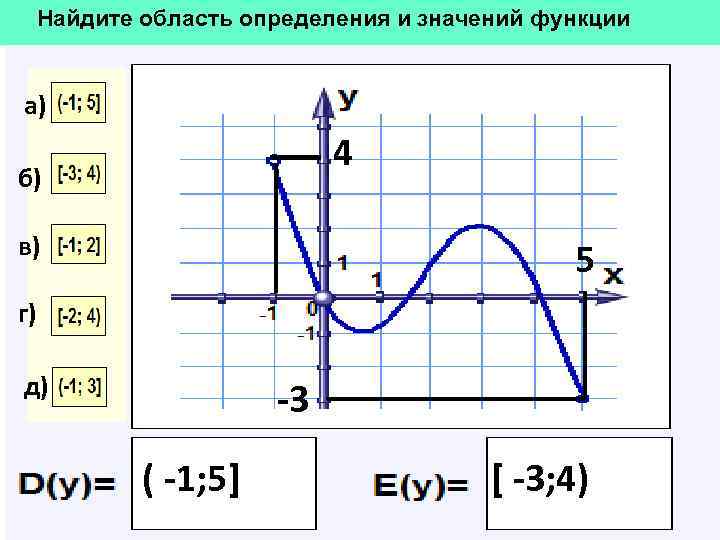Найдите область определения и значений функции а) 4 б) в) 5 г) д) -3 ( -1; 5] [ -3; 4)

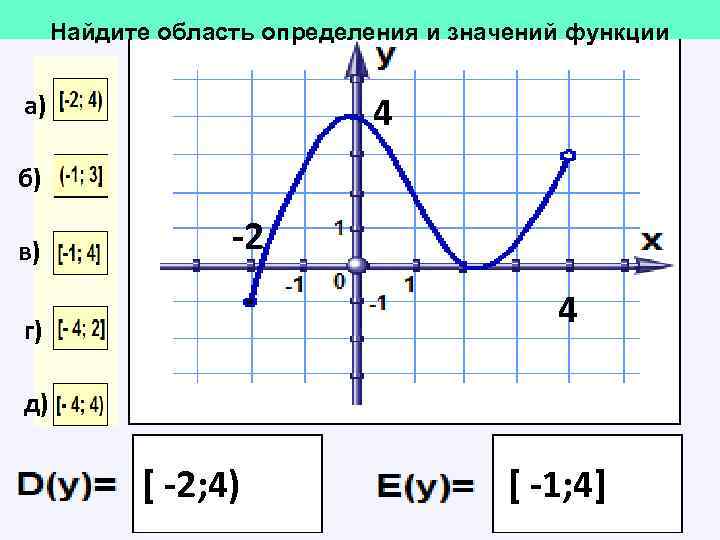Найдите область определения и значений функции 4 а) б) в) -2 4 г) д) [ -2; 4) [ -1; 4]

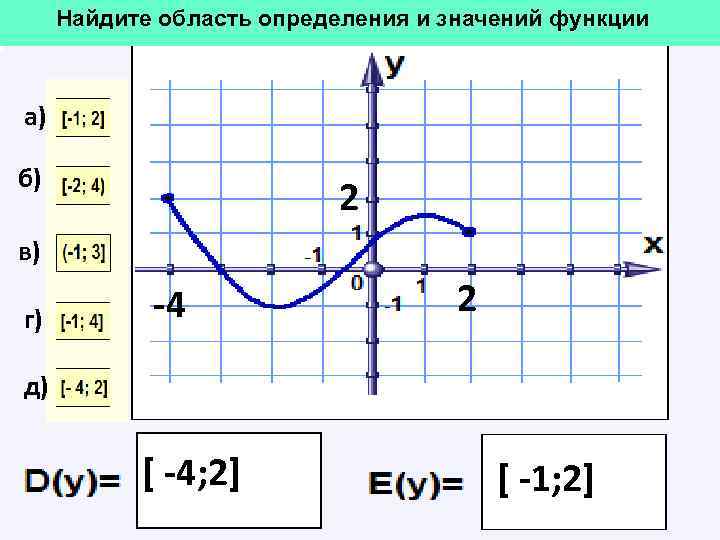Найдите область определения и значений функции а) б) 2 в) г) -4 2 д) [ -4; 2] [ -1; 2]

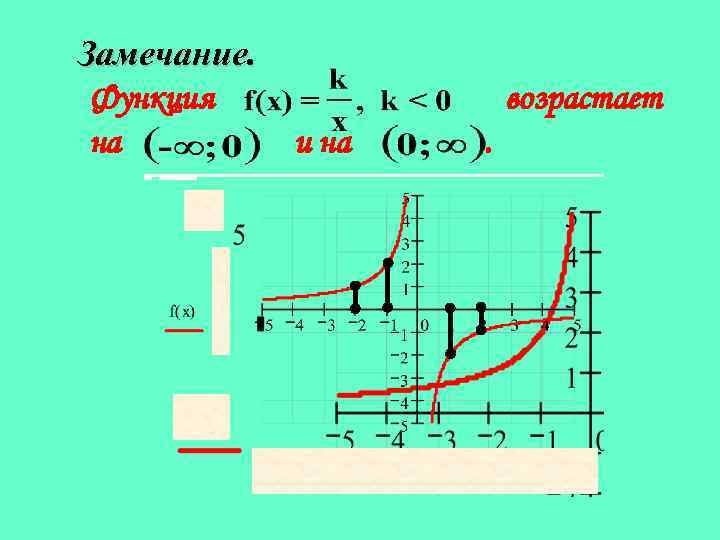Замечание. Функция на возрастает и на .

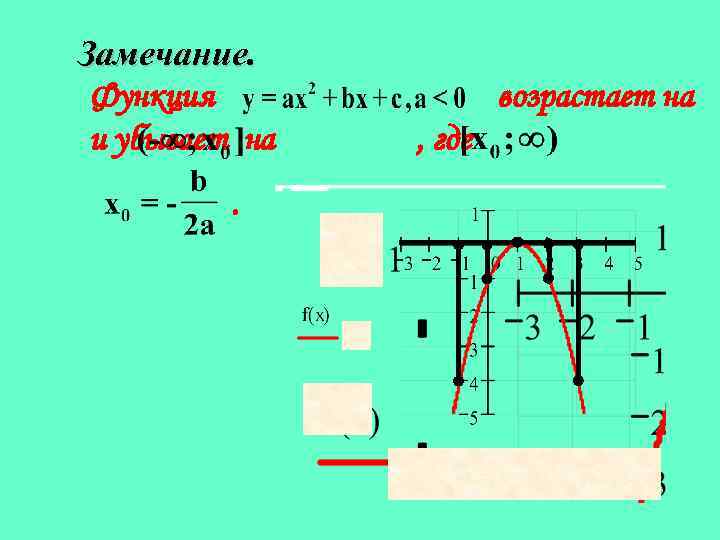Замечание. Функция и убывает на. возрастает на , где

Замечание. Функция убывает на множестве всех действительных чисел.

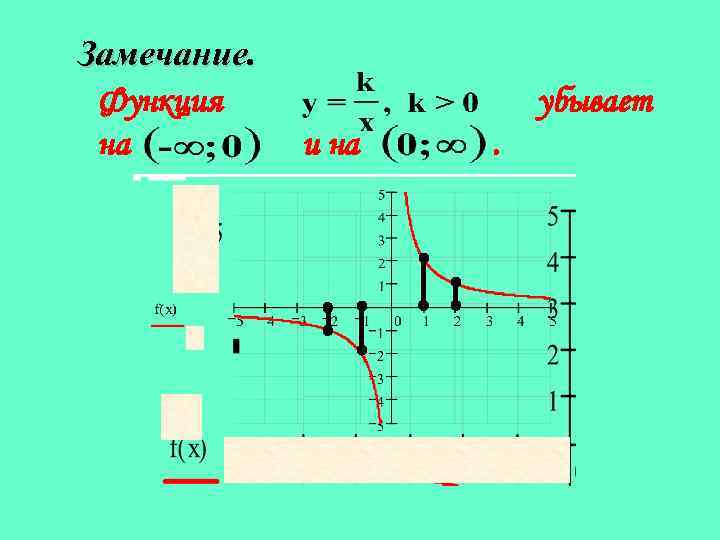Замечание. Функция на убывает и на .

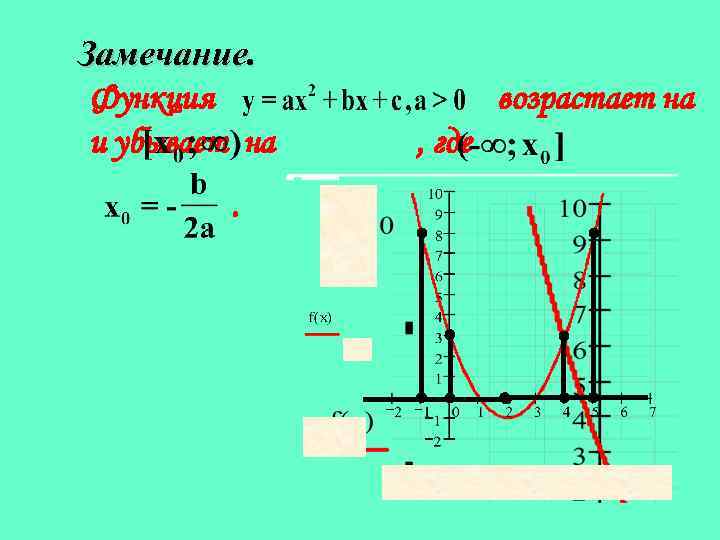Замечание. Функция и убывает на. возрастает на , где