Повторение Определение Прямая называется перпендикулярной к плоскости если

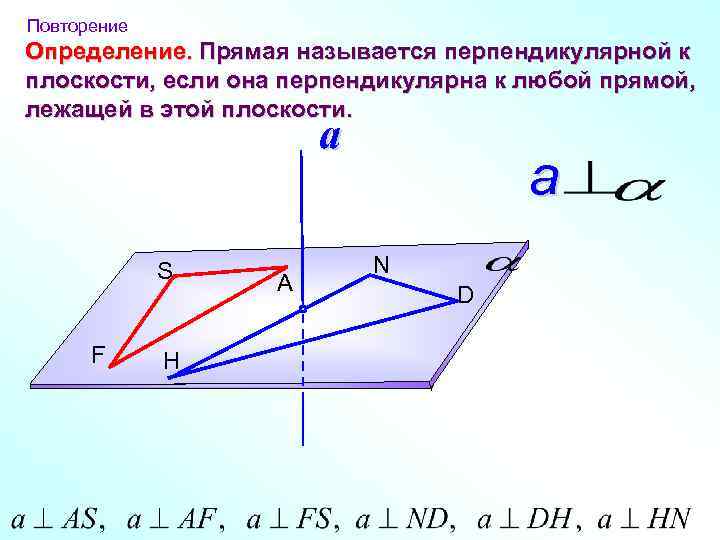Повторение Определение. Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости. a S F H A a N D

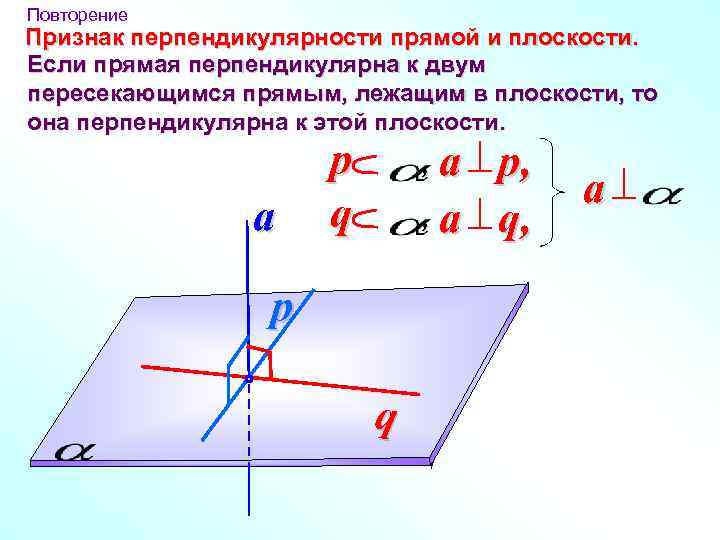Повторение Признак перпендикулярности прямой и плоскости. Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости. a p q a p, , a q, , p q a

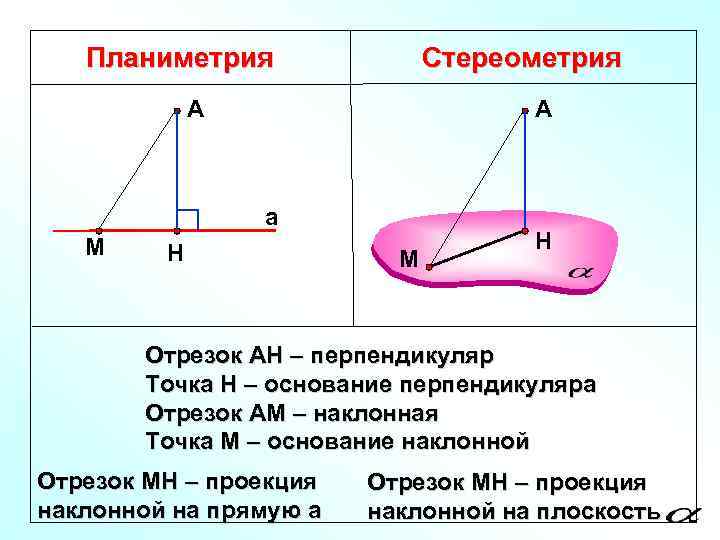Планиметрия Стереометрия А А а М Н Отрезок АН – перпендикуляр Точка Н – основание перпендикуляра Отрезок АМ – наклонная Точка М – основание наклонной Отрезок МН – проекция наклонной на прямую а Отрезок МН – проекция наклонной на плоскость

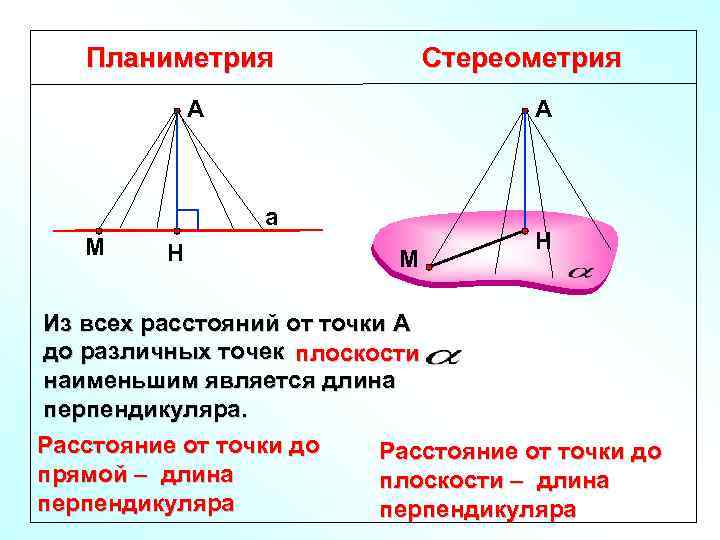Планиметрия Стереометрия А А а М Н Из всех расстояний от точки А до различных точек прямой а плоскости наименьшим является длина перпендикуляра. Расстояние от точки до прямой – длина плоскости – длина перпендикуляра

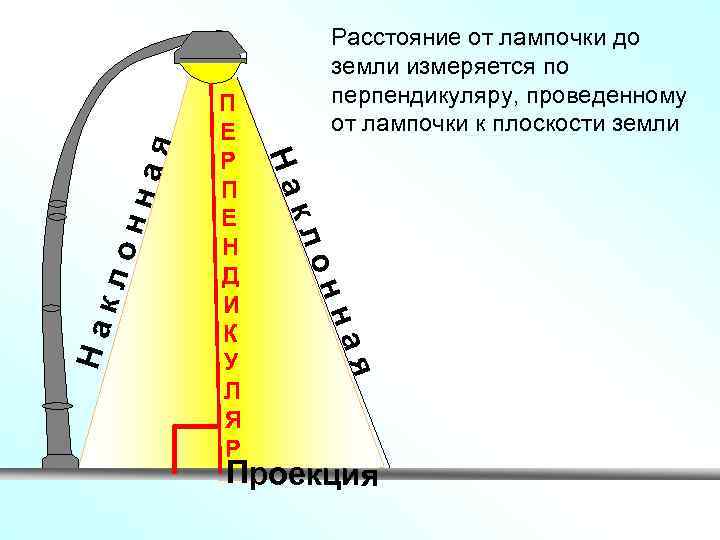я на он он на кл кл я На На П Е Р П Е Н Д И К У Л Я Р Расстояние от лампочки до земли измеряется по перпендикуляру, проведенному от лампочки к плоскости земли Проекция

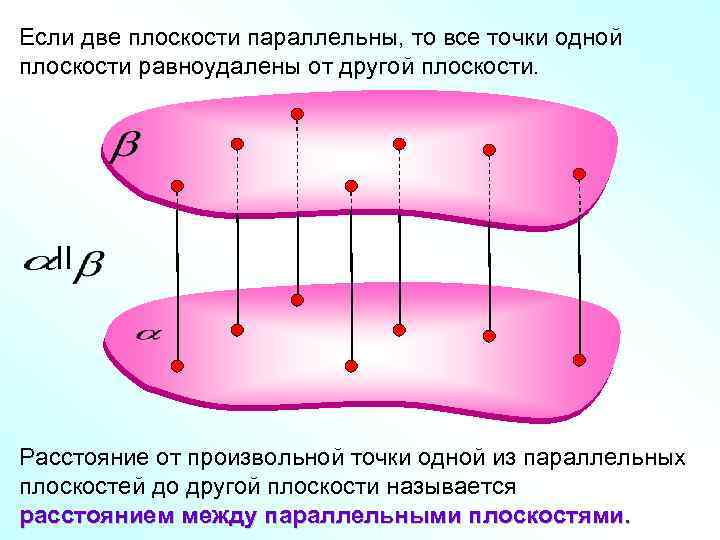Если две плоскости параллельны, то все точки одной плоскости равноудалены от другой плоскости. II Расстояние от произвольной точки одной из параллельных плоскостей до другой плоскости называется расстоянием между параллельными плоскостями.

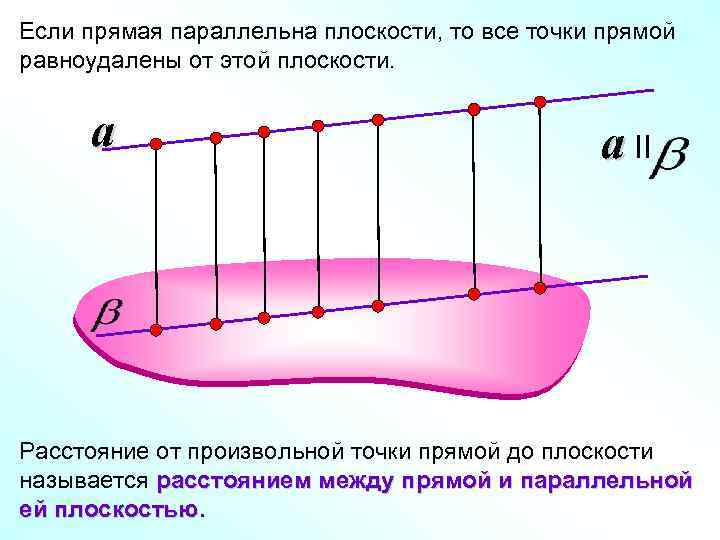Если прямая параллельна плоскости, то все точки прямой равноудалены от этой плоскости. a a II Расстояние от произвольной точки прямой до плоскости называется расстоянием между прямой и параллельной ей плоскостью.

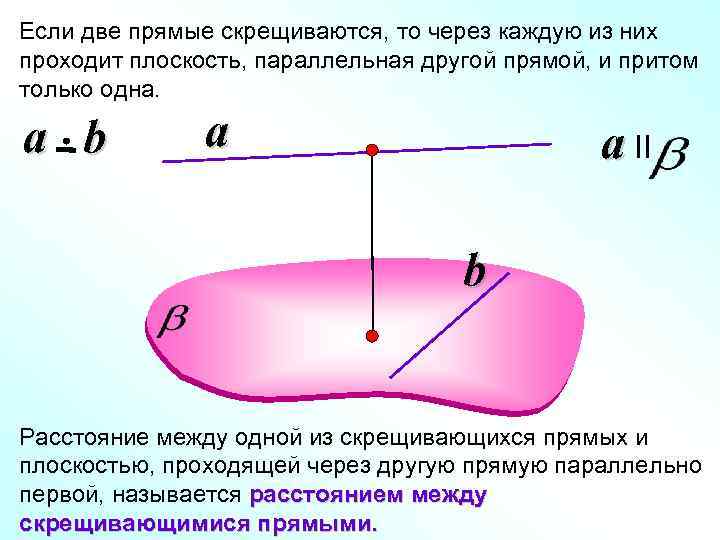Если две прямые скрещиваются, то через каждую из них проходит плоскость, параллельная другой прямой, и притом только одна. a b a a II b Расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой, называется расстоянием между скрещивающимися прямыми.

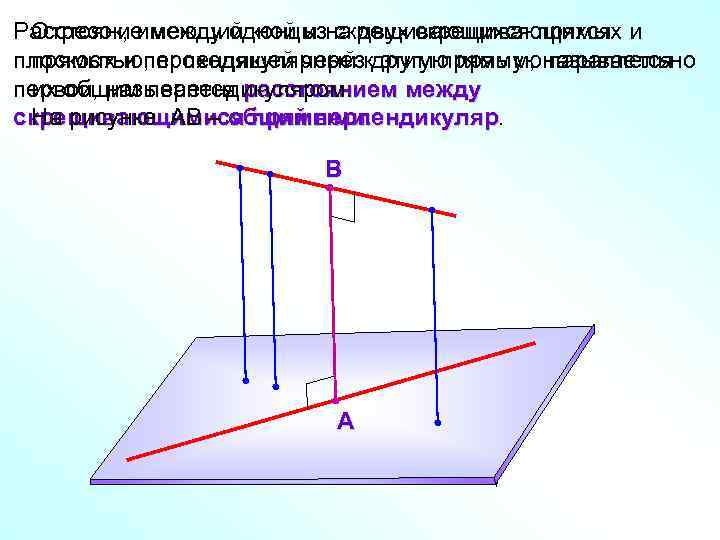Расстояние между одной изна двух скрещивающихся и Отрезок, имеющий концы скрещивающихся прямых плоскостью, проходящей черезкдругую прямуюназывается прямых и перпендикулярный этим прямым, параллельно первой, называется расстоянием между их общим перпендикуляром. скрещивающимися прямыми. На рисунке АВ – общий перпендикуляр В А

В Н-Я П-Я А П-Р С Н-Я П-Я M

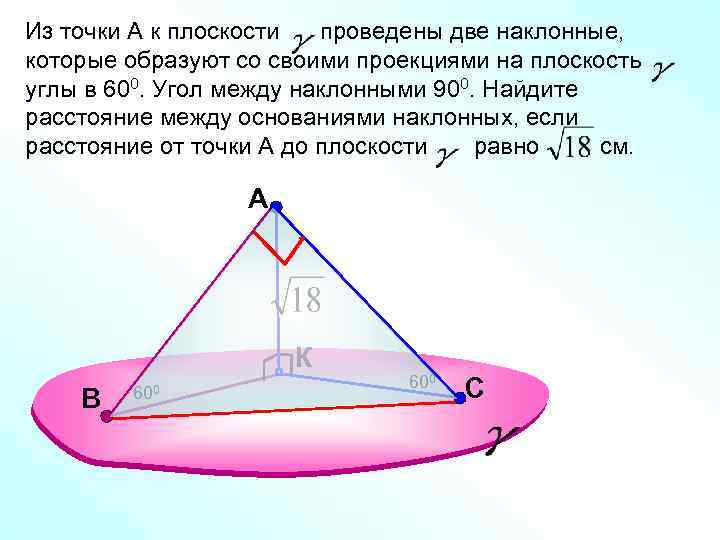Из точки А к плоскости проведены две наклонные, которые образуют со своими проекциями на плоскость углы в 600. Угол между наклонными 900. Найдите расстояние между основаниями наклонных, если расстояние от точки А до плоскости равно см. A К В 600 С

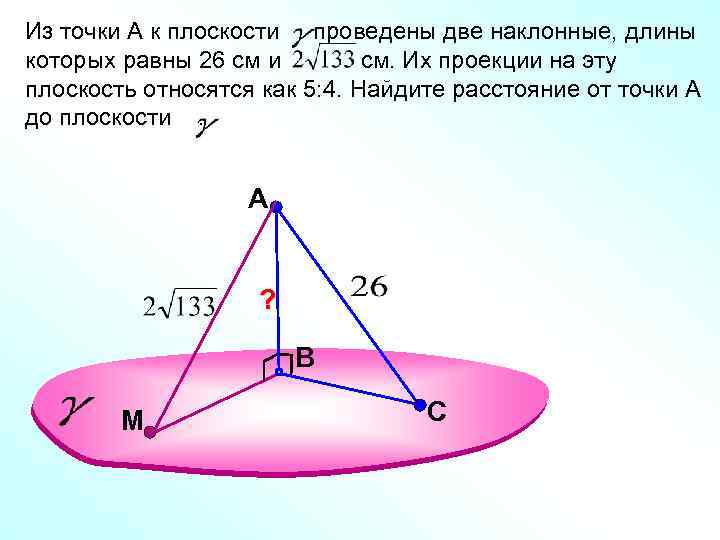Из точки А к плоскости проведены две наклонные, длины которых равны 26 см и см. Их проекции на эту плоскость относятся как 5: 4. Найдите расстояние от точки А до плоскости. A ? В М С

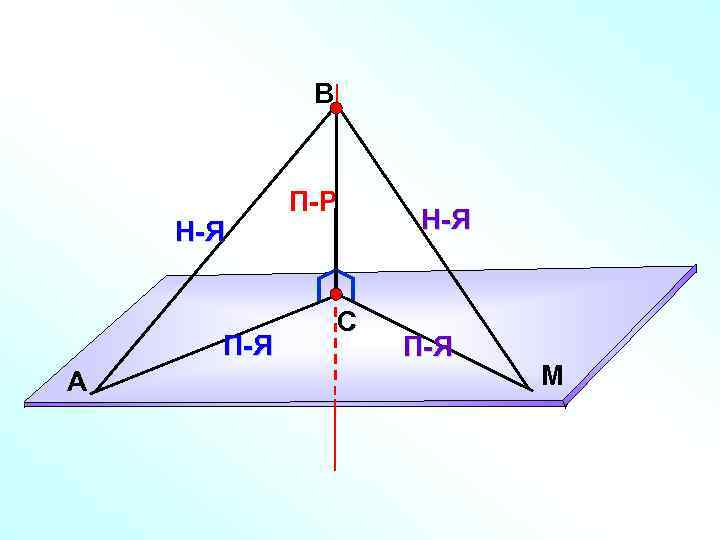
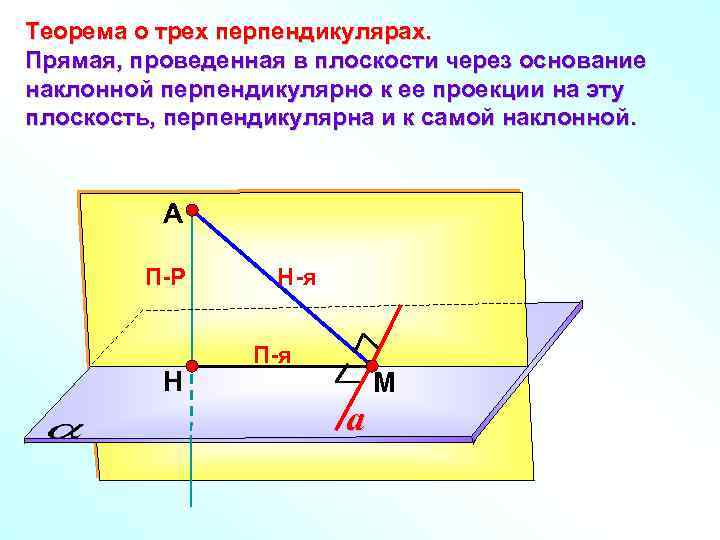Теорема о трех перпендикулярах. Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на эту плоскость, перпендикулярна и к самой наклонной. А П-Р Н Н-я П-я a М

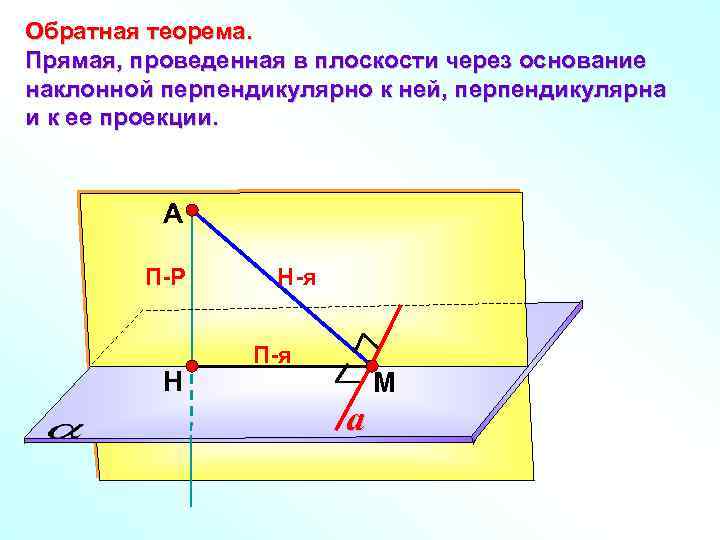Обратная теорема. Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ней, перпендикулярна и к ее проекции. А П-Р Н Н-я П-я a М

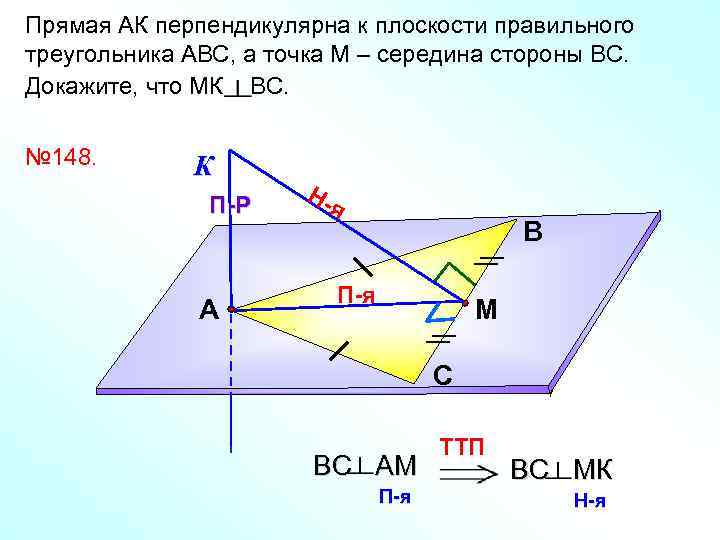Прямая АК перпендикулярна к плоскости правильного треугольника АВС, а точка М – середина стороны ВС. Докажите, что МК ВС. № 148. К П-Р А Ня В П-я М С BC AМ П-я TTП BC MК Н-я

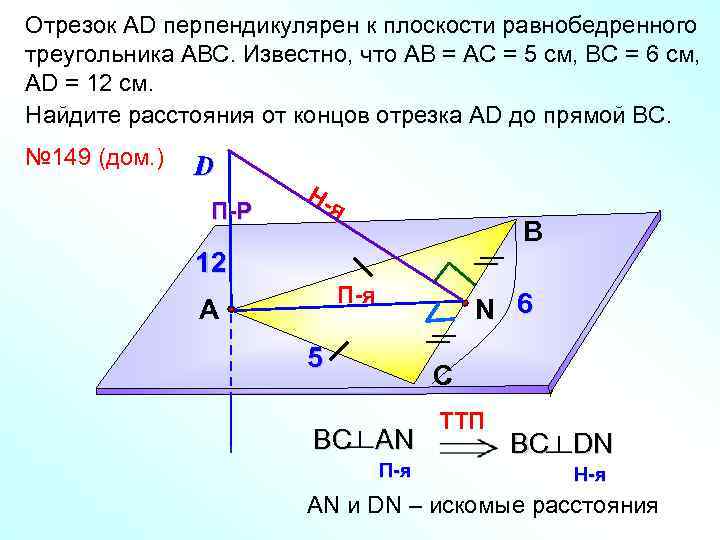Отрезок АD перпендикулярен к плоскости равнобедренного треугольника АВС. Известно, что АВ = АС = 5 см, ВС = 6 см, АD = 12 см. Найдите расстояния от концов отрезка АD до прямой ВС. № 149 (дом. ) D П-Р Ня В 12 П-я А N 6 5 С BC AN П-я TTП BC DN Н-я АN и DN – искомые расстояния

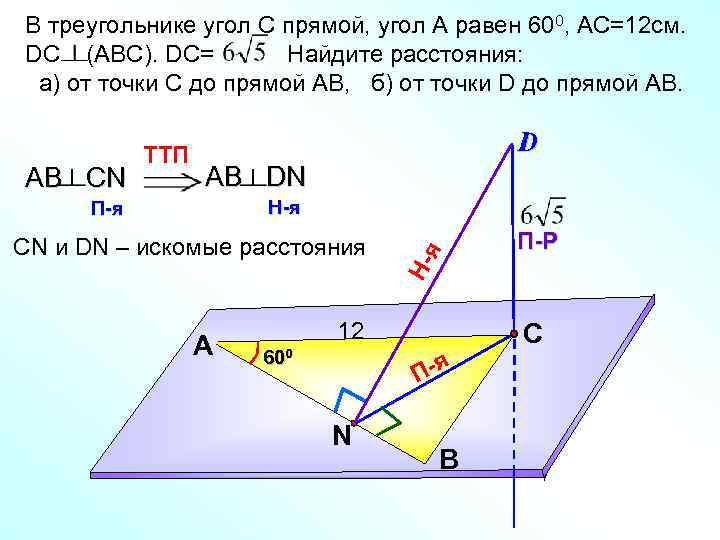В треугольнике угол С прямой, угол А равен 600, AС=12 см. DC (АВС). DC= Найдите расстояния: а) от точки С до прямой АВ, б) от точки D до прямой АВ. D AB DN Н-я П-я CN и DN – искомые расстояния А Ня АВ СN TTП 12 600 С П-я N П-Р В

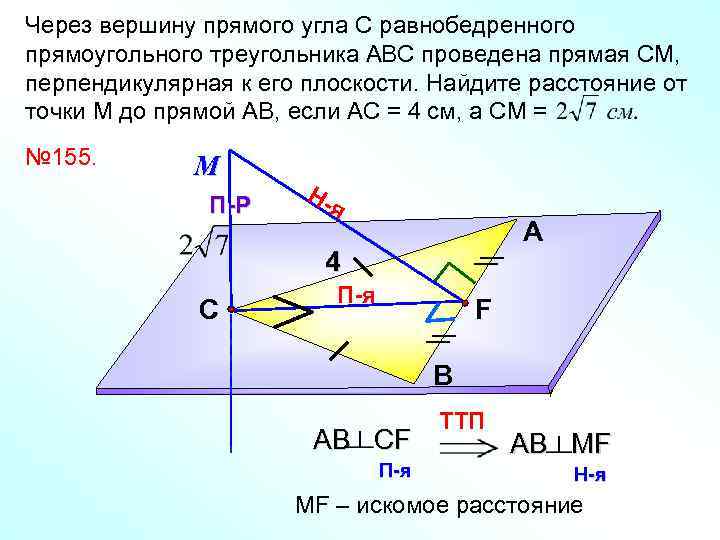Через вершину прямого угла С равнобедренного прямоугольного треугольника АВС проведена прямая СМ, перпендикулярная к его плоскости. Найдите расстояние от точки М до прямой АВ, если АС = 4 см, а СМ = № 155. М П-Р Ня А 4 С П-я F В A В СF П-я TTП AВ MF Н-я МF – искомое расстояние

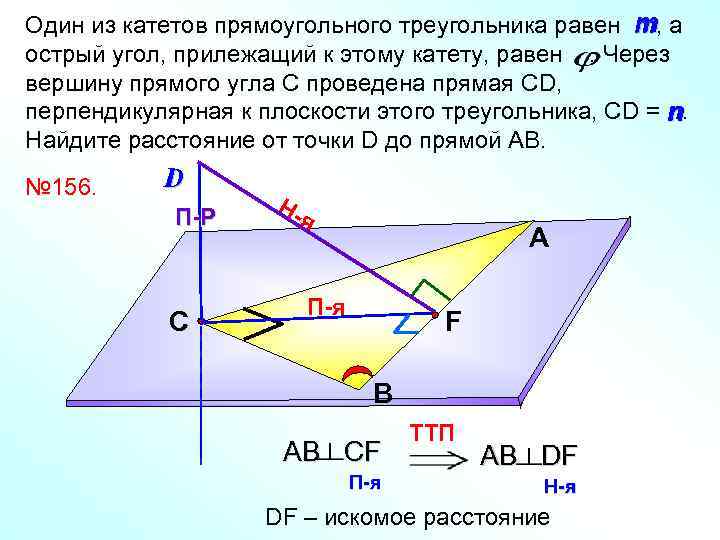Один из катетов прямоугольного треугольника равен т, а т острый угол, прилежащий к этому катету, равен. Через вершину прямого угла С проведена прямая СD, перпендикулярная к плоскости этого треугольника, СD = n. n Найдите расстояние от точки D до прямой АВ. № 156. D П-Р С Ня А П-я F В A В СF П-я TTП AВ DF Н-я DF – искомое расстояние