Повторение Даны точки А 2 -1 0 Назовите

Повторение. Даны точки: А (2; -1; 0) Назовите точки, лежащие в плоскости Оуz. В (0; 0; -7) С (2; 0; 0) D (-4; -1; 0) Назовите точки, лежащие в плоскости Охz. Е (0; -3; 0) F (1; 2; 3) Р (0; 5; -7) К (2; 0; -4) В (0; 0; -7) Назовите точки, лежащие в плоскости Оху. С (2; 0; 0) Е (0; -3; 0)

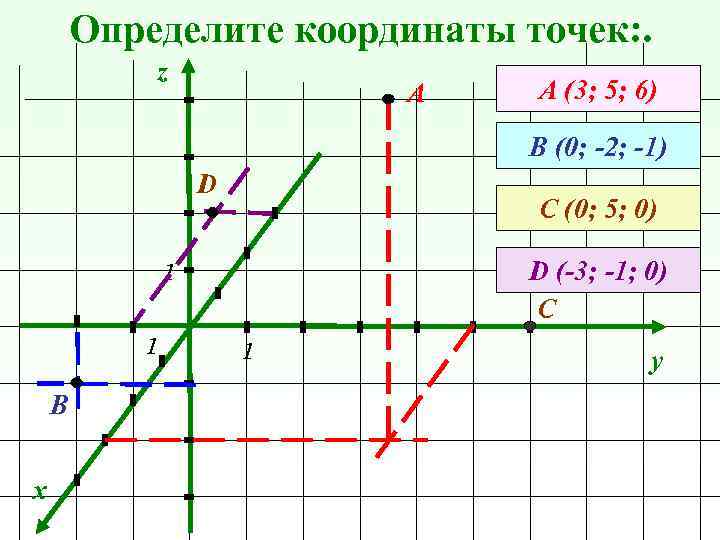Определите координаты точек: . z А А (3; 5; 6) В (0; -2; -1) D С (0; 5; 0) D (-3; -1; 0) С 1 1 В x 1 y

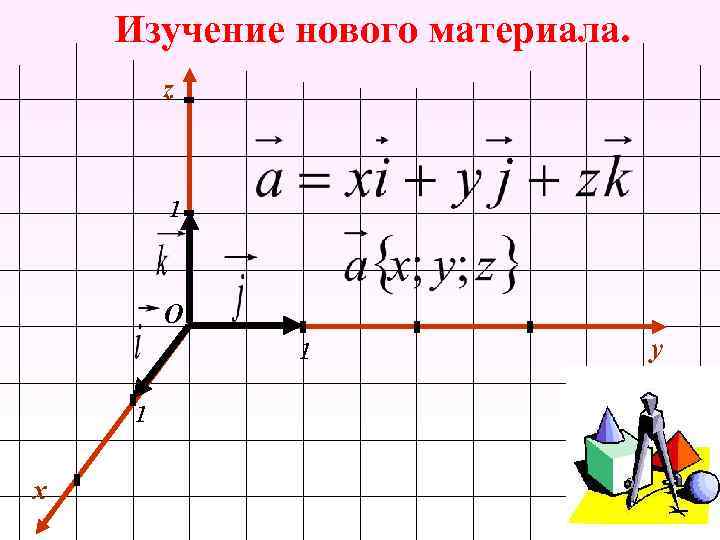Изучение нового материала. z 1 О 1 1 x y

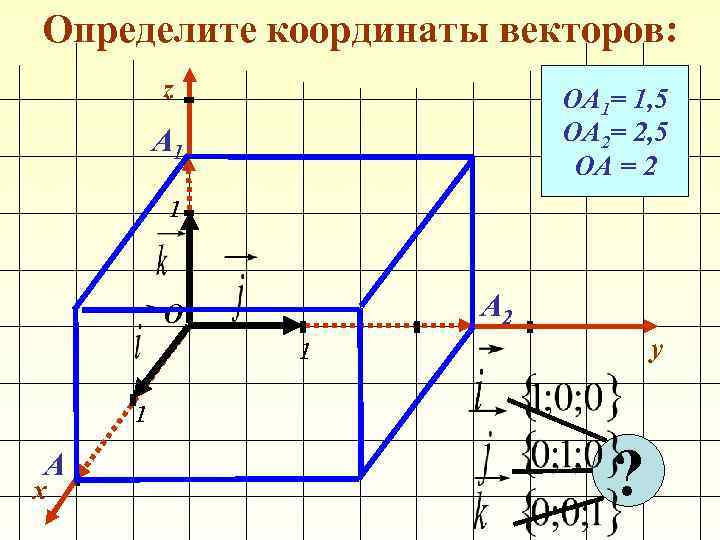Определите координаты векторов: z ОА 1= 1, 5 ОА 2= 2, 5 ОА = 2 А 1 1 А 2 О y 1 1 А x ?

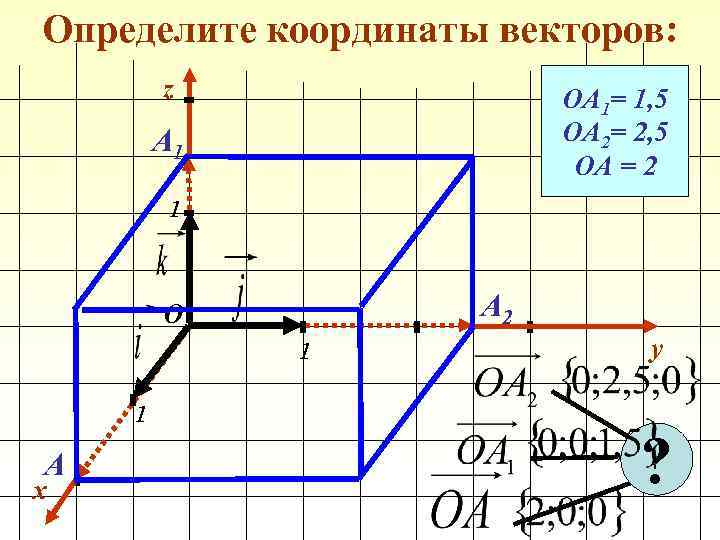Определите координаты векторов: z ОА 1= 1, 5 ОА 2= 2, 5 ОА = 2 А 1 1 А 2 О 1 1 А x y ?

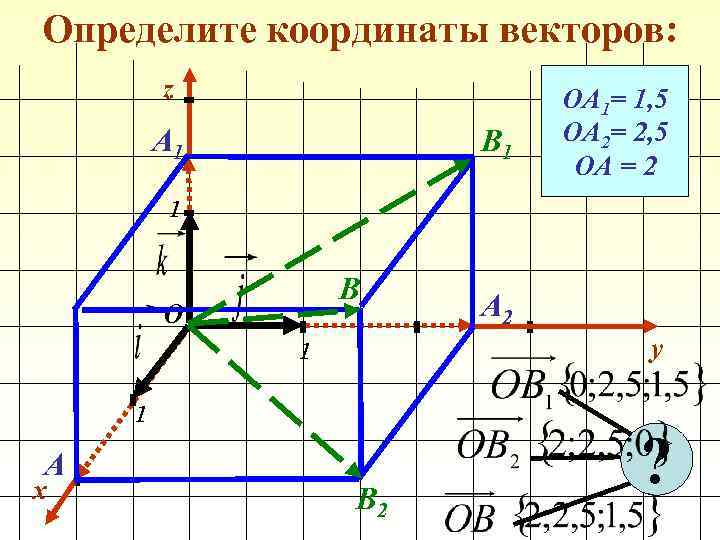Определите координаты векторов: z А 1 В 1 ОА 1= 1, 5 ОА 2= 2, 5 ОА = 2 1 В О y 1 1 А x А 2 В 2 ?

Разложите все векторы по координатным векторам. Проверяем:

Правила действий над векторами с заданными координатами. 1. Равные векторы имеют равные координаты. Пусть , тогда х1 = х2; у1 = у2; z 1 = z 2

Правила действий над векторами с заданными координатами. 2. Каждая координата суммы двух (и более) векторов равна сумме соответствующих координат этих векторов. Дано:

Правила действий над векторами с заданными координатами. 3. Каждая координата произведения вектора на число равна произведению соответствующей координаты на это число. α – произв. число 4. Каждая координата разности двух векторов равна разности соответствующих координат этих векторов.

Домашнее задание: №№ 405, 406. Повторить определение средней линии треугольника и теорему о средней линии треугольника.