ПОВТОРЕНИЕ А Л Г Е Б Р А

ПОВТОРЕНИЕ А Л Г Е Б Р А 9 К Л А С С Использованы КИМ для подготовки к итоговой аттестации. Методическая разработка Савченко Е. М. МОУ гимназия № 1, г. Полярные Зори, Мурманская обл.

На рисунке изображен график квадратичной функции y=f(x) на отрезке [-5; 2]. Найдите f(-8) ПОДУМАЙ ! 1 1 2 Не существует ВЕРНО! 3 5 4 10 7 6 5 4 3 2 1 -7 -6 ПОДУМАЙ -5 -4 -3 -2 -1 -1 1 2 3 4 5 6 7 -2 ! -3 -4 -5 -6 -7 ПОДУМАЙ! Маленький тест

На рисунках показаны графики некоторых функций у=aх2+bx+с. Укажите верную комбинацию. у а<0, D>0 a<0, D>0 у a<0, D<0 х a>0, D>0 0 х a>0, D<0 у у a>0, D>0 a>0, D=0 a>0, D<0 a<0, D>0 a<0, D=0 0 х 0 a<0, D<0 a<0, D=0 х

На рисунке показан график некоторой функции у=aх2+bx+с. Укажите верную комбинацию. ПОМОЩЬ аc>0 D>0, т. к. …. у a>0, т. к. … c. D>0 ab<0 b. D>0 bc>0 х c<0, т. к. … b>0, т. к. …

На рисунке показан график некоторой функции у=aх2+bx+с. Укажите верную комбинацию. ПОМОЩЬ c>0, b<0 D<0, т. к. …. у ab>0, D<0 a<0, т. к. … х ab<0, D<0 c<0, т. к. … b>0, т. к. … аb>0, D>0

Для функции укажите график. у 1 0 у х у 4 2 0 0 Легко найти нули функции х=0, х=1 ПОДУМАЙ! у 3 х Верно! х ПОДУМАЙ ! 0 х

Используя графические представления, подберите из данных уравнений второе уравнение системы так, чтобы она имела одно решение. У у=х+3 1 у = х2 2 у = – х2 3 Два решения 3 2 у=х+3 4 у = – х3 1 Два решения -3 ВЕРНО! -2 -1 1 2 -1 -2 ТРИ решения -3 -4 Маленький тест 3 х

График показывает, как менялась цена акций компании в течение месяца. Определите на сколько процентов снизилась цена акций этой компании? Не верно акций, р Стоимость 1 На 40% 10 Не верно 8 2 3 На 4% На 25% 6 4 ВЕРНО! 2 Не верно 10 4 На 2% 20 30 День месяца

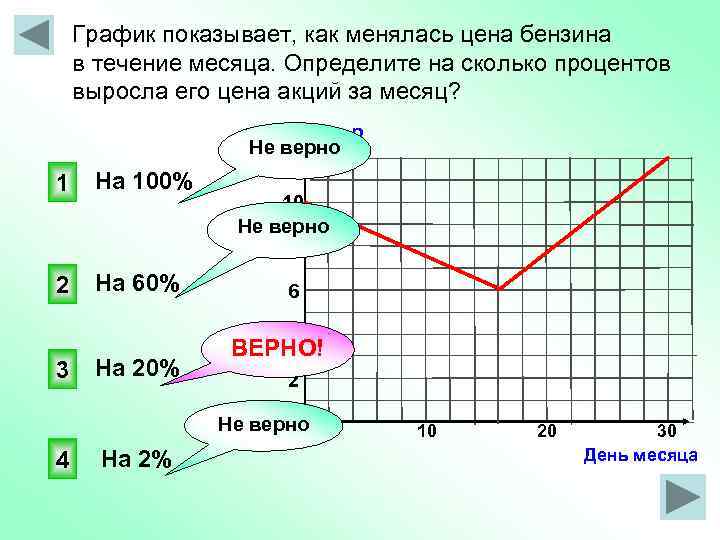
График показывает, как менялась цена бензина в течение месяца. Определите на сколько процентов выросла его цена акций за месяц? Цена, р 1 На 100% 2 На 60% Не верно 12 10 Не верно 8 6 4 3 На 20% ВЕРНО! 2 Не верно 4 На 2% 10 20 30 День месяца

В одной системе координат построены графики функций у=0, 5 х и у=-2 Определите координаты точки их пересечения и найдите сумму этих координат. у у -2, 5 ПОДУМАЙ! 0, 5 -1, 5 х -1 0 -2 -0, 5 ПОДУМАЙ -2 ! у -5 у ПОДУМАЙ! -4+(-2)= - 6 2 -3 Верно! -6 х х 0 -2 х 2 у 0, 5 = -4 х 0 -2 у = -2

Укажите график функции 1 6 6 3 0 ПОДУМАЙ! 2 х 5 у -5 ПОДУМАЙ ! 6 0 6 4 у = 6 х + 5 х 0 Верно! 0 ПОДУМАЙ! х

На рисунке показан график некоторой функции y=ax 2+bx+c. Найдите формулу, задающую эту функцию. у ------ 1 -5 -4 -3 -2 -1 I I I -I ---- -3 ----- у = –х2 – 4 х – 3 I I у = –х2+4 х – 3 х у = х2+4 х – 3. у = –х2 – 4 х+3

На рисунке показан график некоторой функции у=aх2+bx+с. Укажите верную комбинацию. ПОМОЩЬ c>0, b<0 D<0, т. к. …. у ab<0, D<0 a<0, т. к. … х ab>0, D<0 c<0, т. к. … b<0, т. к. … ac<0,

На рисунке показан график некоторой функции у=aх2+bx+с. Укажите верную комбинацию. ПОМОЩЬ c. D>0 у D>0, т. к. …. ac>0 a<0, т. к. … х ac<0, c>0, т. к. … b. D<0, ab>0

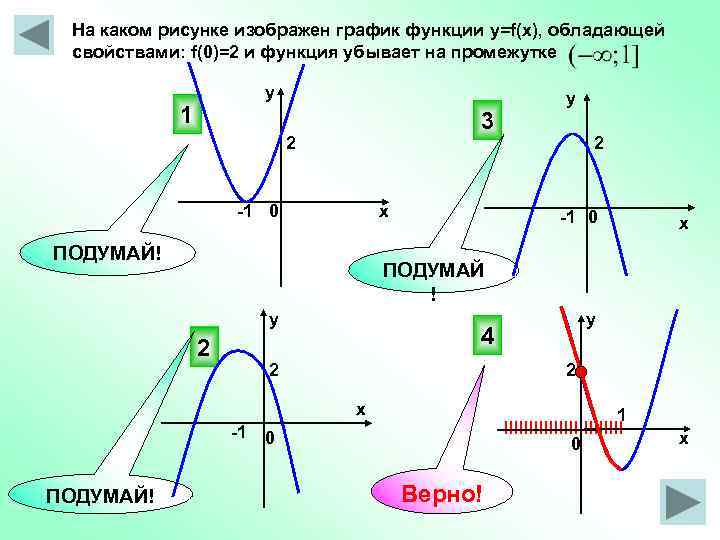
На каком рисунке изображен график функции y=f(x), обладающей свойствами: f(0)=2 и функция убывает на промежутке у 1 3 2 -1 0 х ПОДУМАЙ! 2 -1 0 х ПОДУМАЙ ! у 2 2 -1 у 4 2 х ПОДУМАЙ! у 1 IIIIIIIIIIII 0 0 Верно! х

Для функции укажите график. у 1 0 у х у 4 2 0 0 Легко найти нули функции х=0, х=1 ПОДУМАЙ! у 3 х Верно! х ПОДУМАЙ ! 0 х

Сколько решений имеет система у 4 ВЕРНО! 3 1 Нет решений Не верно 2 Одно решение Не верно-3 2 3 4 -2 -1 -1 -2 Два решения -3 Не верно Три решения 1 1 2 3 х

Сколько решений имеет система у 4 Не верно 1 Нет решений 2 ВЕРНО! Одно решение 3 2 Не верно -3 -2 1 -1 -1 -2 3 Два решения -3 Не верно 4 Три решения 1 2 3 х

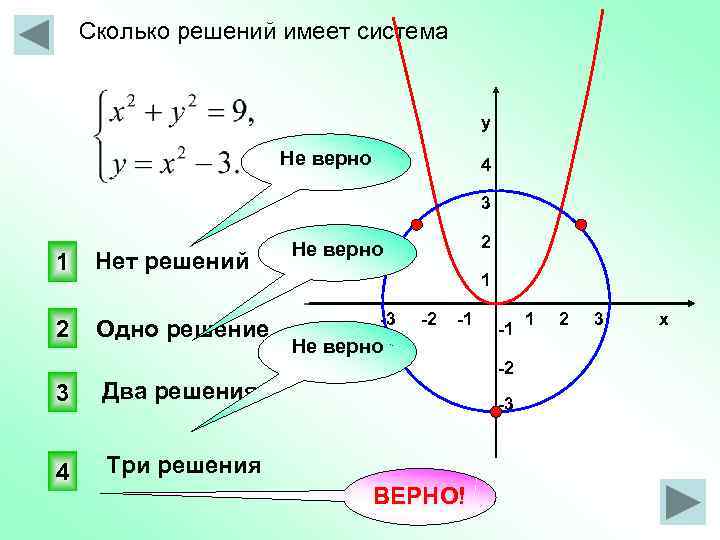
Сколько решений имеет система у Не верно 4 3 1 Нет решений 2 Одно решение 3 1 -3 -2 -1 Не верно -1 -2 Два решения 4 2 Не верно Три решения -3 ВЕРНО! 1 2 3 х

Сколько решений имеет система у 4 ВЕРНО! Не верно 3 2 1 1 Нет решений 2 Одно решение Не верно -1 -3 -2 -1 -2 -3 3 Два решения Не верно 4 Три решения 1 2 3 х

Используя графические представления, подберите из данных уравнений второе уравнение системы так, чтобы она имела одно решение. У у=х+3 1 у = х2 2 у = – х2 3 Два решения 3 2 у=х+3 4 у = – х3 1 Два решения -3 ВЕРНО! -2 -1 1 -1 -2 ТРИ решения -3 -4 2 3 х

Используя графические представления, подберите из данных уравнений второе уравнение системы так, чтобы она не имела одно решения. У Два решения 1 у = х2 2 у = – х2 3 2 -3 ВЕРНО! 3 4 1 Два решения -2 -1 1 -1 -2 ДВА решения -3 -4 2 3 х

Функция задана формулой y= – 2(x+2)2+3, где Выполни построение. Сумма наибольшего и У наименьшего значений 3 функции равна 2 1 – 4 ВЕРНО! 1 Не верно 2 – 2 3 6 4 12 -3 Не верно -2 IIIII -1 1 -1 -2 Не верно -3 -4 -5 2 3 х