Повторение a b a b cos a b

Повторение a b = a b cos(a b ) a b =0 Û a ^b a b > 0 Û a b < 900 a b < 0 Û a b > 900 a 2 = a 2

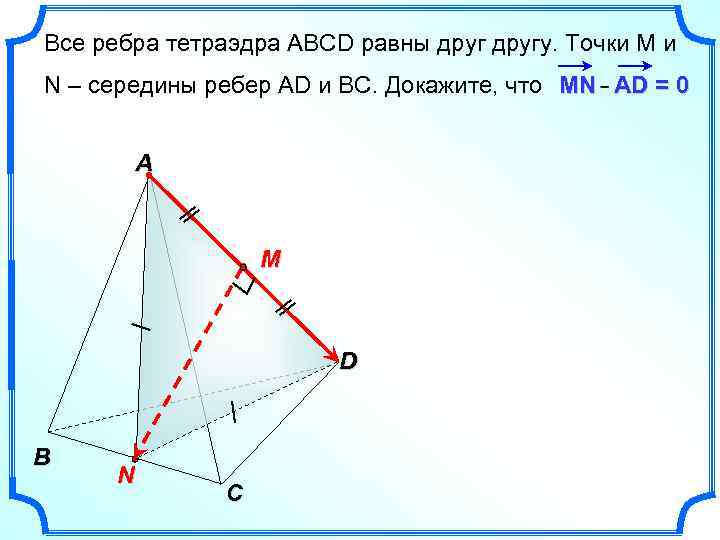
Все ребра тетраэдра АВСD равны другу. Точки М и N – середины ребер АD и ВС. Докажите, что MN AD = 0 A M D B N C

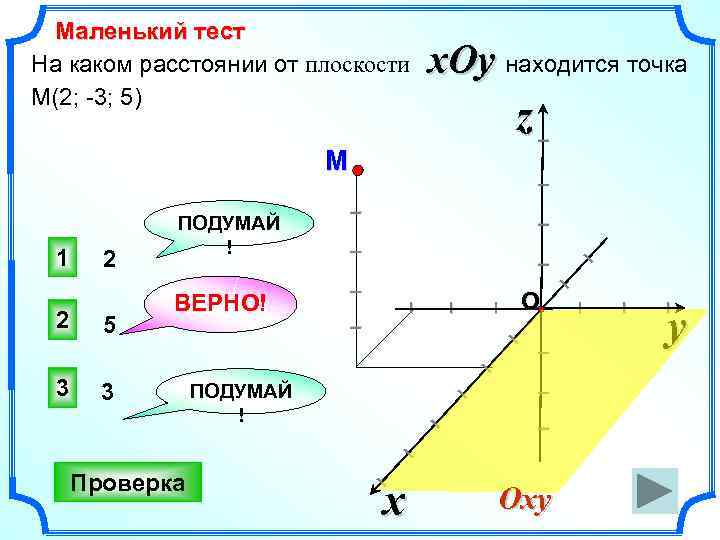
x. Oy находится точка z I Маленький тест На каком расстоянии от плоскости М(2; -3; 5) 5 3 I I O I I I I ПОДУМАЙ ! x I Проверка Oxy I I 3 I I 2 ВЕРНО! I 2 I 1 ПОДУМАЙ ! I I M I I I y

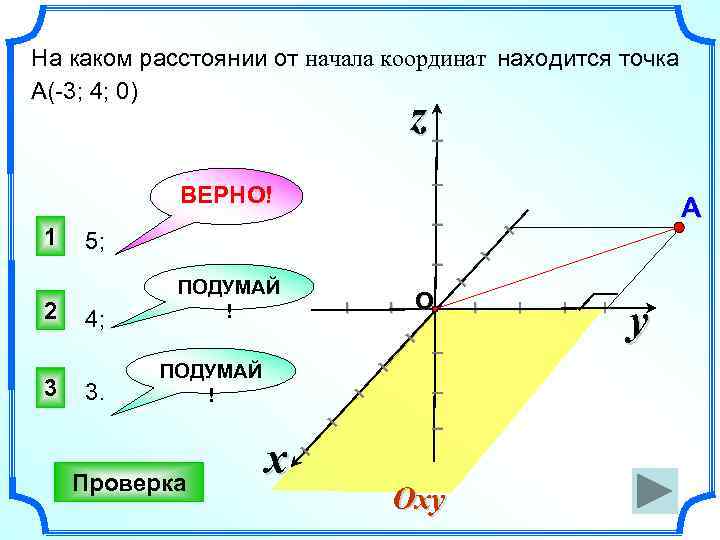
На каком расстоянии от начала координат находится точка А(-3; 4; 0) I z I А I I 5; 4; I I O I I 2 ПОДУМАЙ ! I I Проверка x I I I 3 ПОДУМАЙ ! Oxy I I 1 I ВЕРНО! I I y

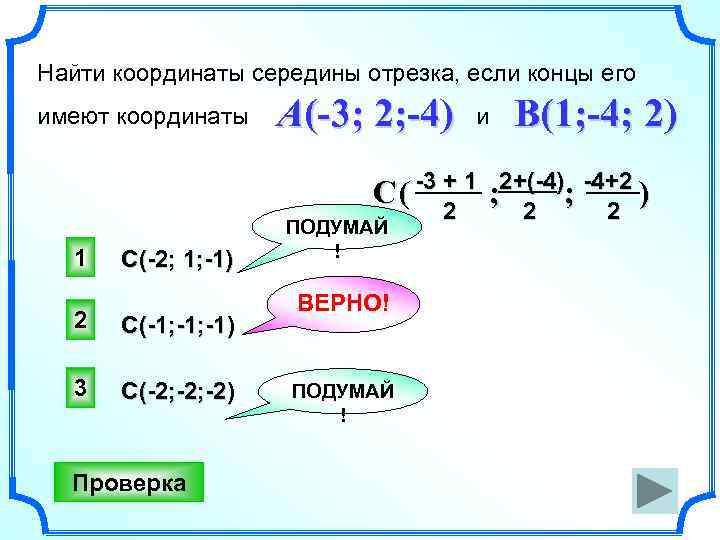
Найти координаты середины отрезка, если концы его имеют координаты A(-3; 2; -4) и B(1; -4; 2) C ( -3 + 1 ; 2+(-4); -4+2 ) 2 2 2 1 C(-2; 1; -1) 2 C(-1; -1) 3 C(-2; -2) Проверка ПОДУМАЙ ! ВЕРНО! ПОДУМАЙ ! 2 2 2

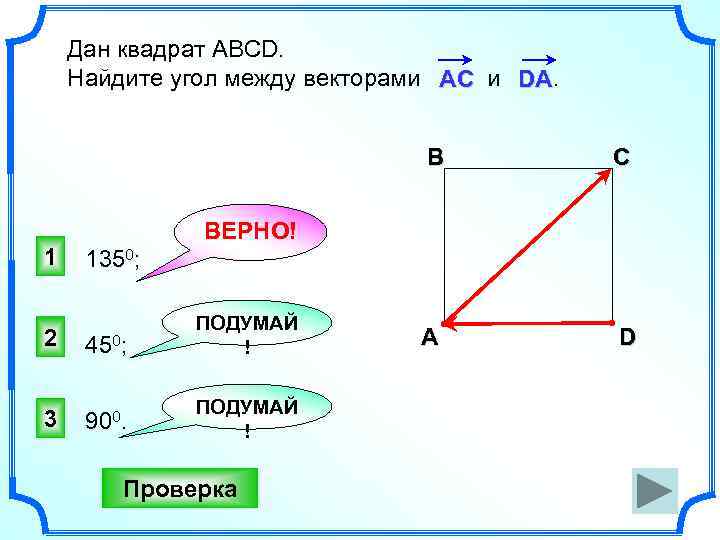
Дан квадрат АВСD. Найдите угол между векторами АС и DA. В 1 С А D ВЕРНО! 1350; 2 450; ПОДУМАЙ ! 3 900. ПОДУМАЙ ! Проверка

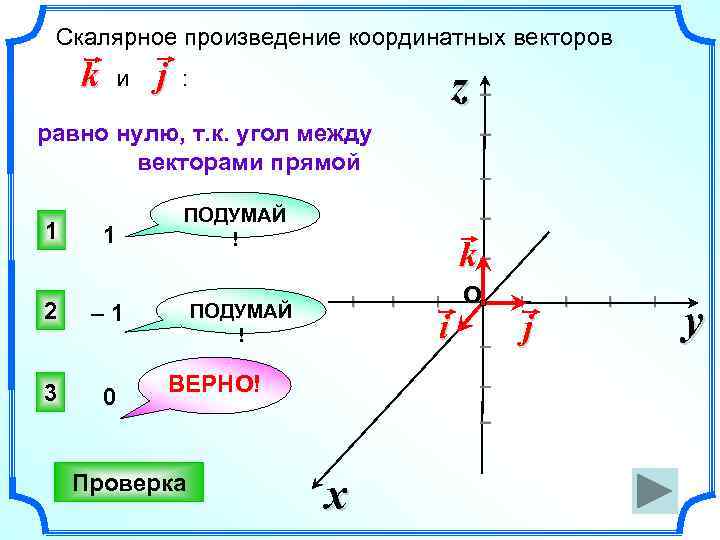
k и j z : I I равно нулю, т. к. угол между векторами прямой I Скалярное произведение координатных векторов 1 I k I 1 ПОДУМАЙ ! 0 ВЕРНО! i O I 3 I I – 1 ПОДУМАЙ ! I I 2 I Проверка x I j I I I y

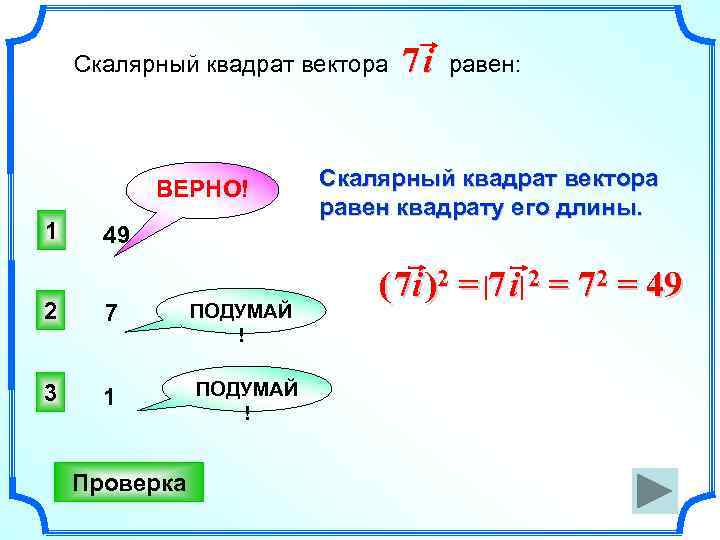
Скалярный квадрат вектора ВЕРНО! 1 49 2 7 ПОДУМАЙ ! 3 1 ПОДУМАЙ ! Проверка 7 i равен: Скалярный квадрат вектора равен квадрату его длины. ( 7 i )2 = 7 i 2 = 72 = 49

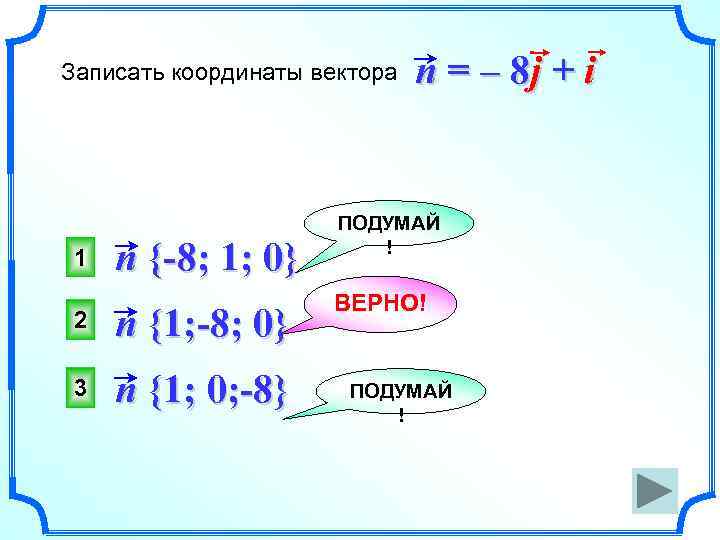
Записать координаты вектора 1 n {-8; 1; 0} 2 n {1; -8; 0} 3 n {1; 0; -8} n = – 8 j + i ПОДУМАЙ ! ВЕРНО! ПОДУМАЙ !

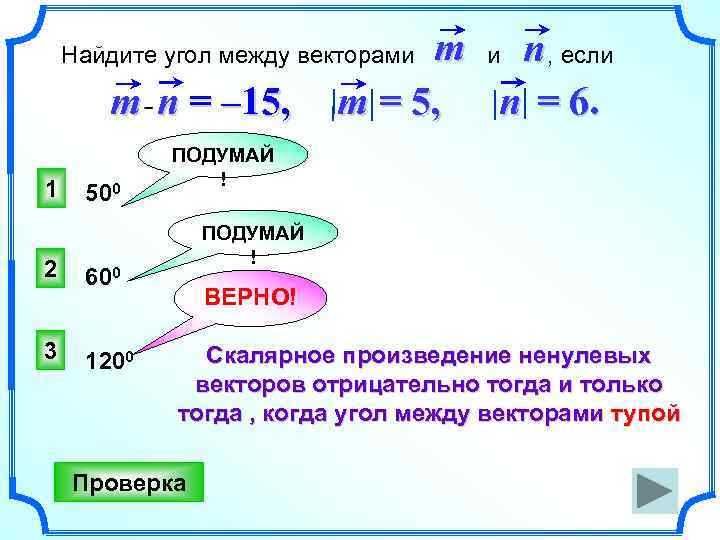
m и n , если m = 5, n = 6. Найдите угол между векторами m n = – 15, 1 2 3 500 ПОДУМАЙ ! 600 1200 ВЕРНО! Скалярное произведение ненулевых векторов отрицательно тогда и только тогда , когда угол между векторами тупой Проверка

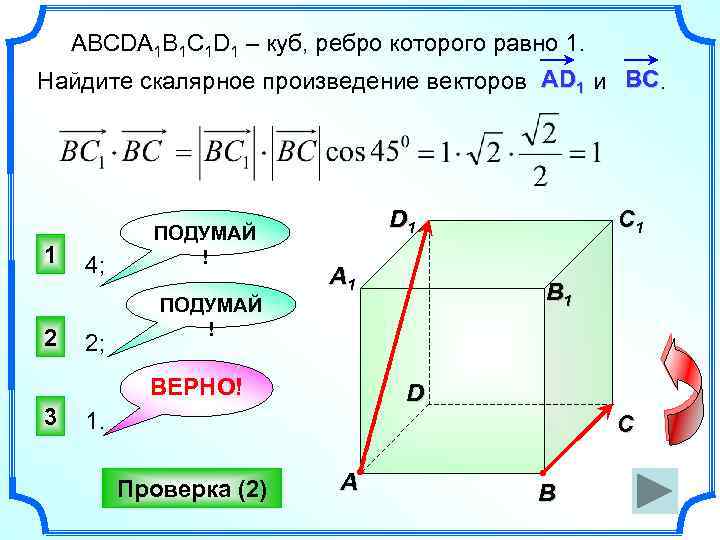
ABCDA 1 B 1 C 1 D 1 – куб, ребро которого равно 1. Найдите скалярное произведение векторов АD 1 и BC. 1 2 4; 2; ПОДУМАЙ ! D 1 A 1 ВЕРНО! 3 C 1 B 1 D 1. C Проверка (2) A B

Скалярное произведение векторов a {x 1; y 1; z 1} выражается формулой Пример и b {x 2; y 2; z 2} a b = x 1 x 2 + y 1 y 2+z 1 z 2 Найдите скалярное произведение векторов b {-2 ; 1 -7} 1; -7 + -3 d { 5 ; 4; -3} + ( ) = 15

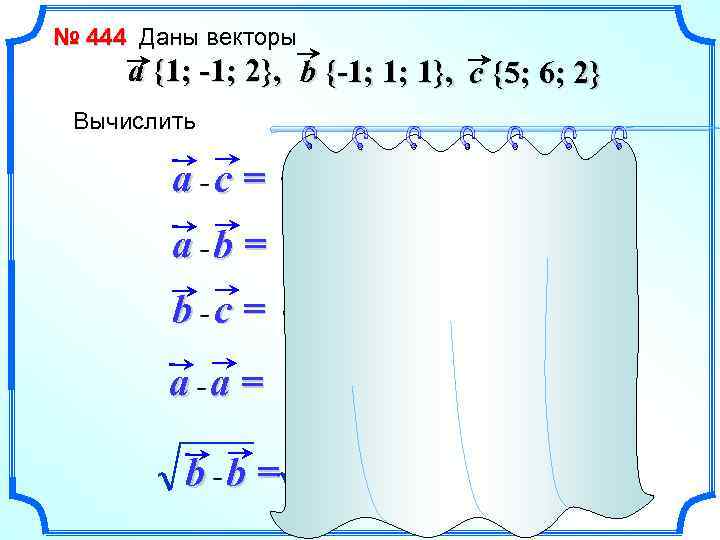
№ 444 Даны векторы a {1; -1; 2}, b {-1; 1; 1}, c {5; 6; 2} Вычислить a c= 1 5 + (-1) 6 + 2 2 = 3 a b= 1 (-1) + (-1) 1 + 2 1 = 0 b c= -1 5 + 1 6 + 1 2 = 3 a a= 1 1 + (-1) + 2 2 = 6 b b= -1 (-1) + 1 1 = 3

Скалярное произведение векторов Через длины векторов и угол между ними в координатах a b = a b cos(a b ) a b = x 1 x 2+y 1 y 2+z 1 z 2 a b =0 Û a ^b a b > 0 Û a b < 900 a b < 0 Û a b > 900 a 2 = a 2

a {3; -4; 2}, b {-2; 1; 3}, c {-2; -1, 5; 0} Найдите a b=3 (-2) + (-4) 1 + 2 3 = - 4 b c = (-2) + 1 c a = 3 (-2) + (-4) тупой (- 1, 5) + 3 0 = 2, 5 (- 1, 5) + 2 0 = 0 Перпендикулярны ли векторы ü острый прямой a и b , b и c, c и a Каким (острым, тупым или прямым) является угол между векторами a и b, b и c, c и a

Косинус угла между ненулевыми векторами aи b выражается формулой cos a = x 1 x 2 + y 1 y 2 + z 1 z 2 x 12 + y 12 + z 12 x 22 + y 22 + z 22

Доказательство: ü a b = x 1 x 2 + y 1 y 2+ z 1 z 2 a = x 12 + y 12 + z 12 ü b = x 22 + y 22 + z 22 ü a b = a b cosa = = a b

Свойства скалярного произведения векторов a b, c Для любых векторов , справедливы равенства: 1 a 2³ 0 2 a b 3 (a + b ) c = и любого числа k причем a 2> 0 b a Переместительный закон = при a ¹ 0 a c+b c Распределительный закон 4 ( k a ) b = k ( a b) Сочетательный закон

(a + b ) c = a c+b c Распределительный закон имеет место для любого числа слагаемых. Например, (a+b+c) d = a d+b d +c d

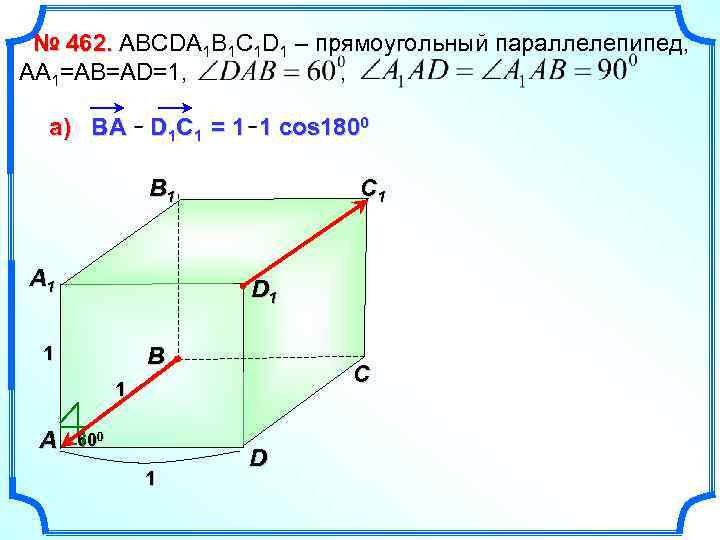
№ 462. ABCDA 1 B 1 C 1 D 1 – прямоугольный параллелепипед, АА 1=АВ=АD=1, , а) ВА D 1 C 1 = 1 1 cos 1800 B 1 A 1 C 1 D 1 1 B C 1 A 600 1 D

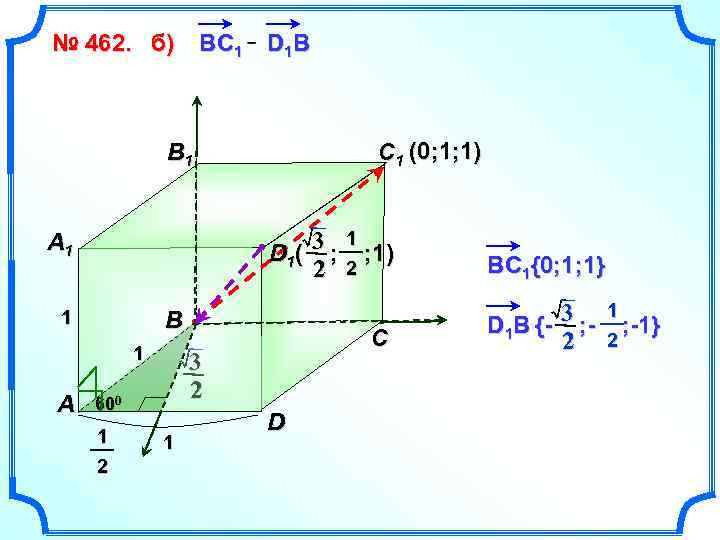
№ 462. б) В C 1 D 1 B C 1 (0; 1; 1) B 1 3 ; 1) D 1 ( 2 2 A 1 1 B 1 A 3 2 600 1 2 C 1 D ВC 1{0; 1; 1} 3 D 1 B {- ; 2 1 ; -1} 2

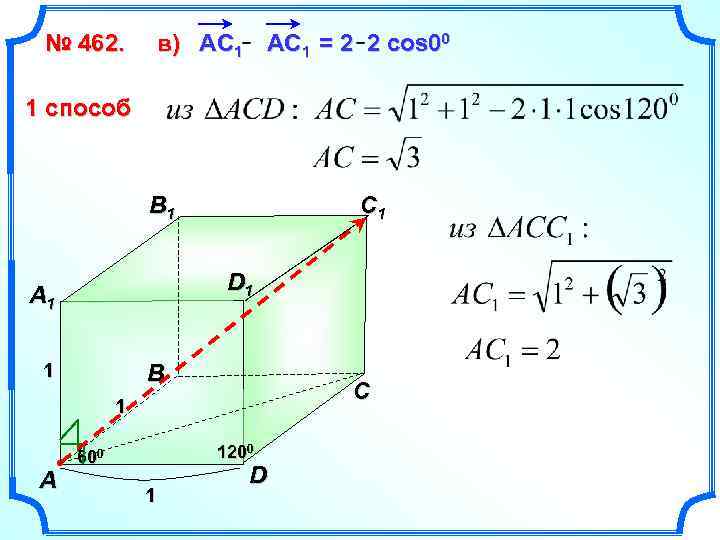
№ 462. в) АС 1 АC 1 = 2 2 cos 00 1 способ B 1 C 1 D 1 A 1 1 B C 1 A 1200 600 1 D

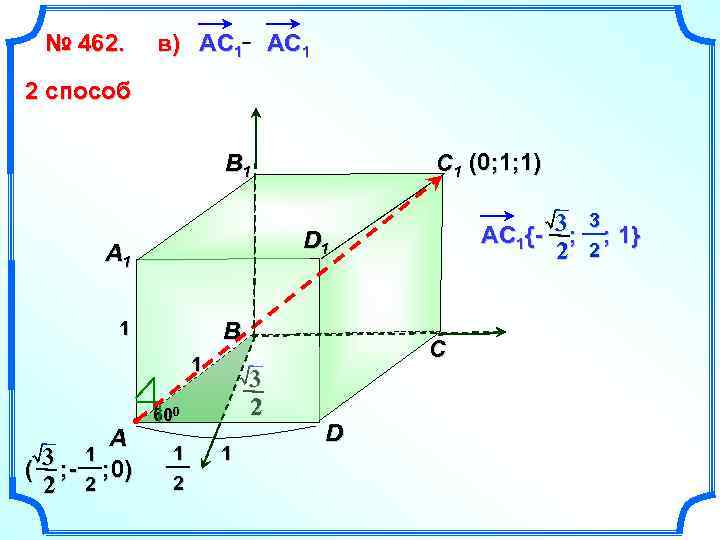
№ 462. в) АС 1 АC 1 2 способ C 1 (0; 1; 1) B 1 D 1 A 1 1 B 1 A 3 ; - 1 ; 0) ( 2 2 3 АС 1{- ; 2 3 2 600 1 2 C 1 D 3 ; 1} 2

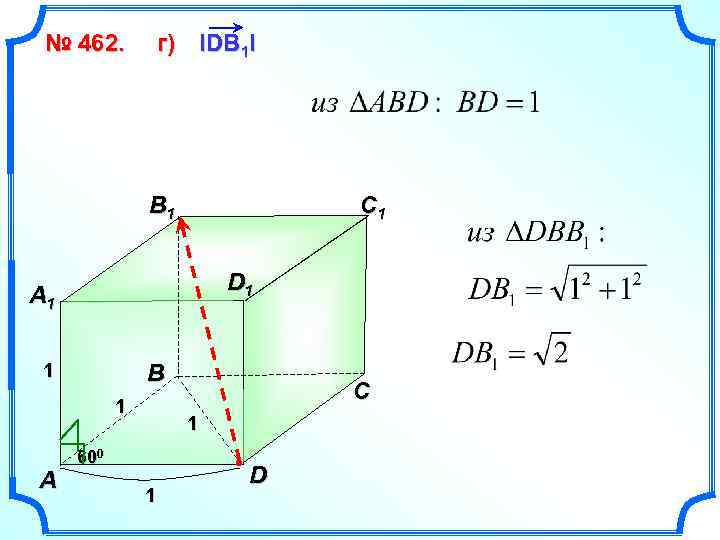
№ 462. г) IDB 1 I B 1 C 1 D 1 A 1 1 B 1 A C 1 600 1 D

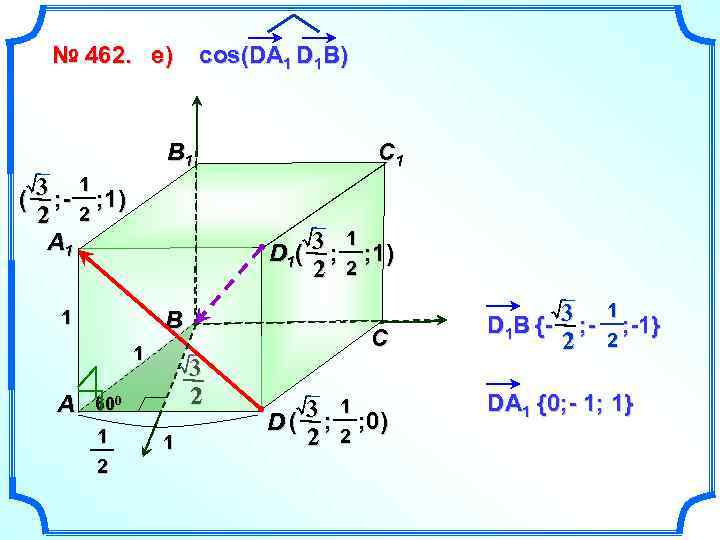
№ 462. е) cos(DA 1 D 1 B) B 1 3 ; - 1 ; 1) ( 2 2 A 1 3 ; 1) D 1 ( 2 2 1 B 1 A C 3 2 600 1 2 C 1 1 3 ; 1 ; 0) D( 2 2 3 D 1 B {- ; 2 1 ; -1} 2 DA 1 {0; - 1; 1}

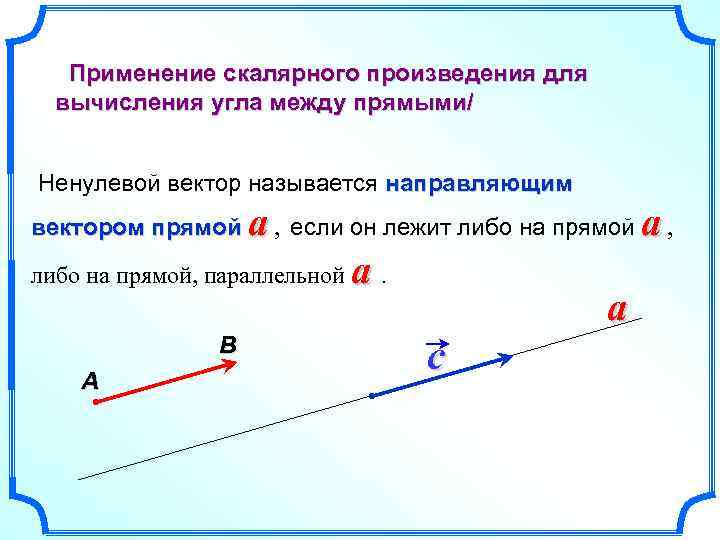
Применение скалярного произведения для вычисления угла между прямыми/ Ненулевой вектор называется направляющим a , если он лежит либо на прямой a , либо на прямой, параллельной a. a B c A вектором прямой A

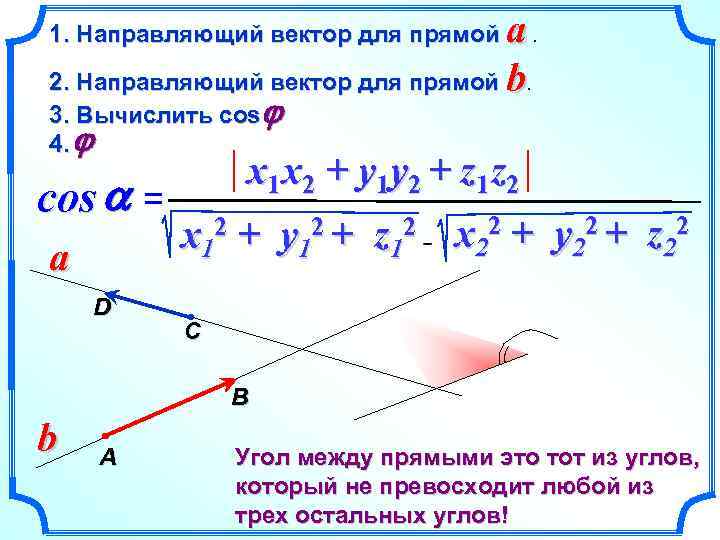
a. 2. Направляющий вектор для прямой b. 1. Направляющий вектор для прямой 3. Вычислить cos j 4. j cos a = a D x 1 x 2 + y 1 y 2 + z 1 z 2 x 12 + y 12 + z 12 x 22 + y 22 + z 22 C B b A Угол между прямыми это тот из углов, который не превосходит любой из трех остальных углов!

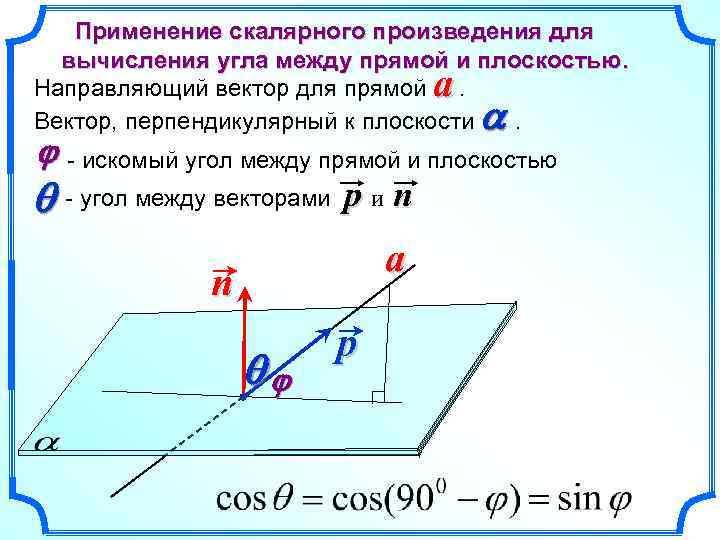
Применение скалярного произведения для вычисления угла между прямой и плоскостью. Направляющий вектор для прямой. Вектор, перпендикулярный к плоскости. a a j - искомый угол между прямой и плоскостью q - угол между векторами p и n a n qj p

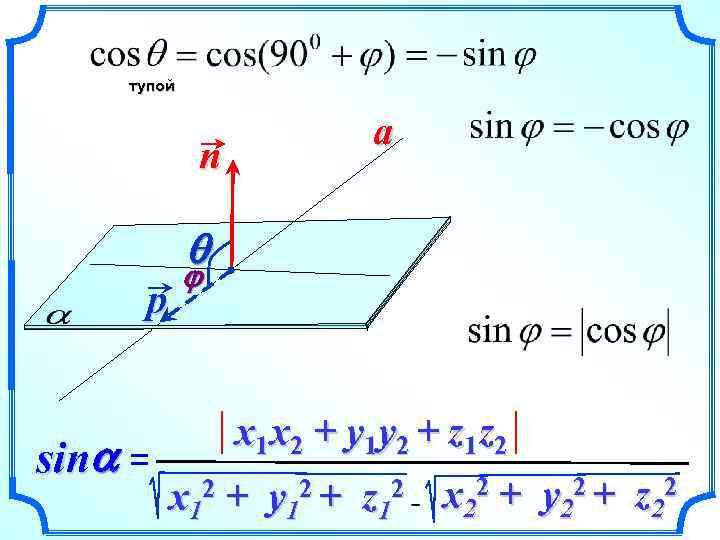
тупой a n q p sina = j x 1 x 2 + y 1 y 2 + z 1 z 2 x 12 + y 12 + z 12 x 22 + y 22 + z 22

Применение скалярного произведения для вычисления угла между прямой и плоскостью. a 1. Направляющий вектор для прямой. 2. Вектор, перпендикулярный к плоскости 3. Вычислить sin j 4. j sina = a. x 1 x 2 + y 1 y 2 + z 1 z 2 x 12 + y 12 + z 12 x 22 + y 22 + z 22