Поволжский государственный технологический университет Анализ временных рядов и

Поволжский государственный технологический университет Анализ временных рядов и прогнозирование Разработчик: профессор каф. ЛТ и Л, д-р. с. -х. наук Черных В. Л.

Анализ временных рядов и прогнозирование Анализ временных рядов основывается на предположении, что последовательные значения данных наблюдаются через равные промежутки времени Основные цели анализа временных рядов: • определение природы ряда • прогнозирование (предсказание будущих значений временного ряда по настоящим и прошлым значениям).

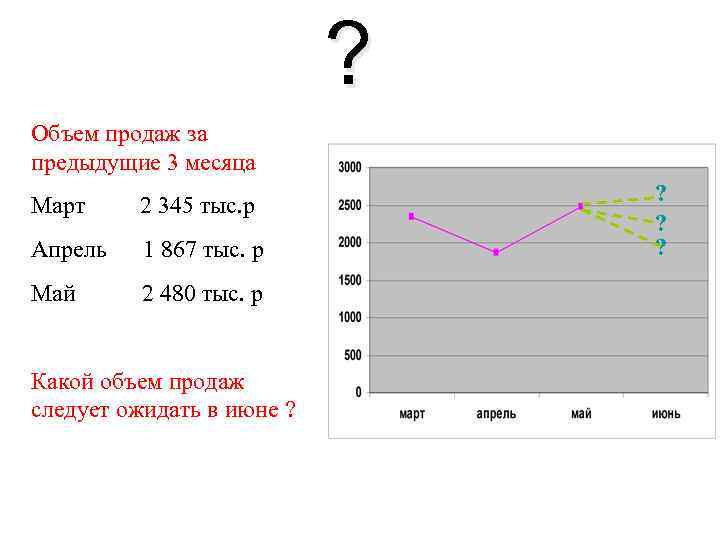? Объем продаж за предыдущие 3 месяца Март 2 345 тыс. р Апрель 1 867 тыс. р Май 2 480 тыс. р Какой объем продаж следует ожидать в июне ? ? ? ?

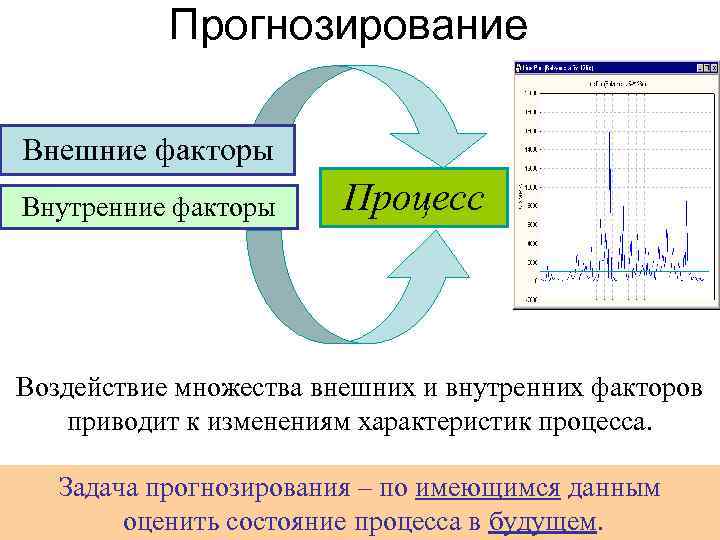Прогнозирование Внешние факторы Внутренние факторы Процесс Воздействие множества внешних и внутренних факторов приводит к изменениям характеристик процесса. Задача прогнозирования – по имеющимся данным оценить состояние процесса в будущем.

Прогнозируемые показатели Таксационные показатели; Параметры управления запасами; Объем выпуска продукции; Объем закупок; Объем продаж; Изменение числа клиентов; Жизненный цикл изделия И т. д.

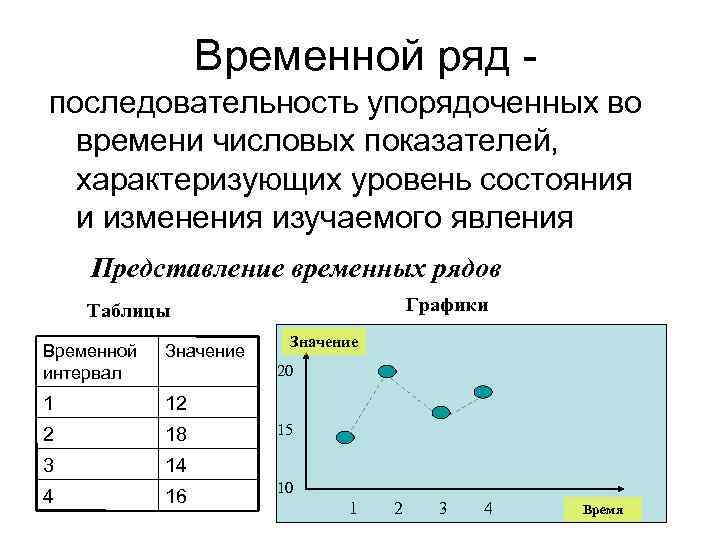Временной ряд последовательность упорядоченных во времени числовых показателей, характеризующих уровень состояния и изменения изучаемого явления Представление временных рядов Графики Таблицы Временной интервал Значение 1 12 2 18 3 14 4 16 Значение 20 15 10 1 2 3 4 Время

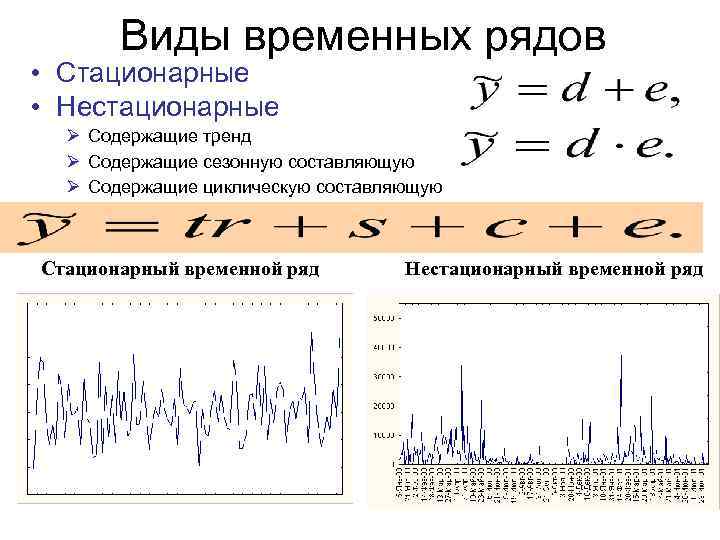Виды временных рядов • Стационарные • Нестационарные Содержащие тренд Содержащие сезонную составляющую Содержащие циклическую составляющую Стационарный временной ряд Нестационарный временной ряд

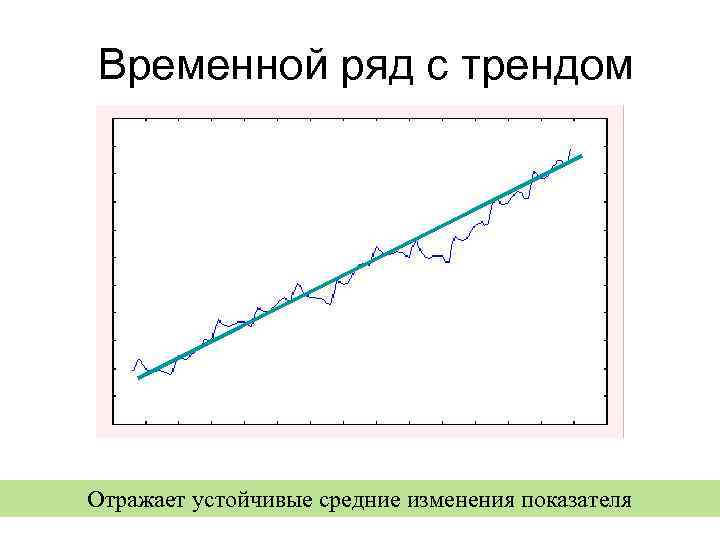Временной ряд с трендом Отражает устойчивые средние изменения показателя

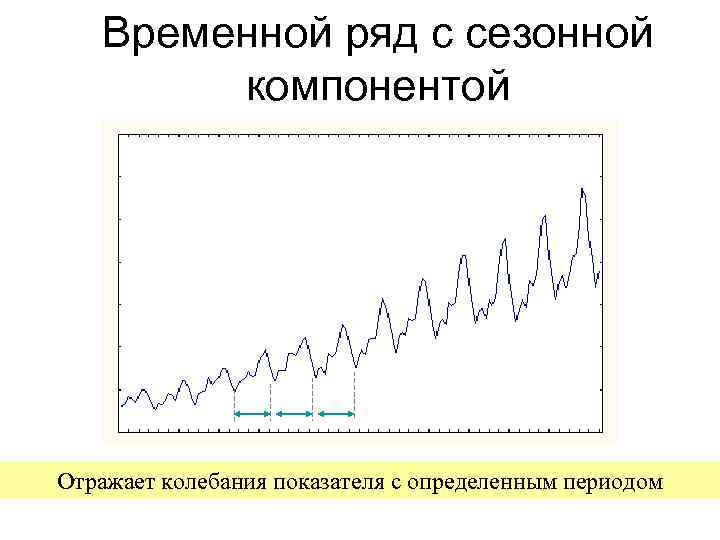Временной ряд с сезонной компонентой Отражает колебания показателя с определенным периодом

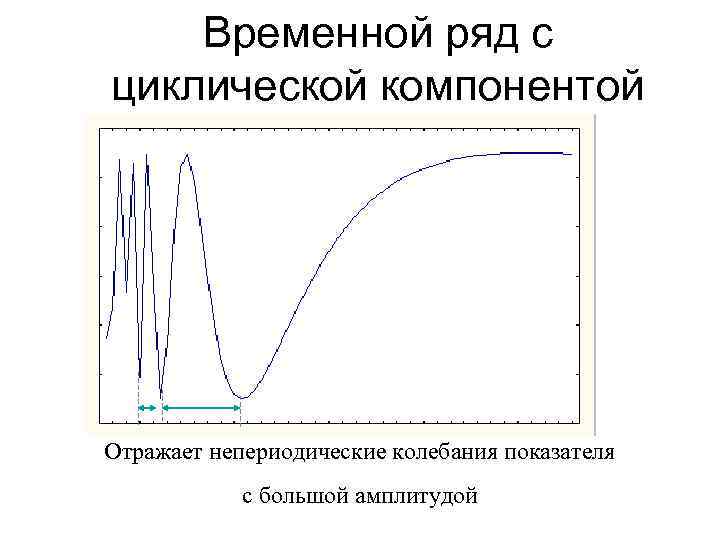Временной ряд с циклической компонентой Отражает непериодические колебания показателя с большой амплитудой

Прогнозирование для стационарных процессов На практике для стационарности ряда достаточно выполнения трех условий: E[yt] не зависит от t, При N>30 прогноз оправдается с D[yt] постоянная, вероятностью 0, 75. (Для нормального распределения - с вероятностью 0, 95) Cov[yt, ys] - функция t-s. E[yt] Прогноз оправдается с вероятностью 0, 89 (0, 997)

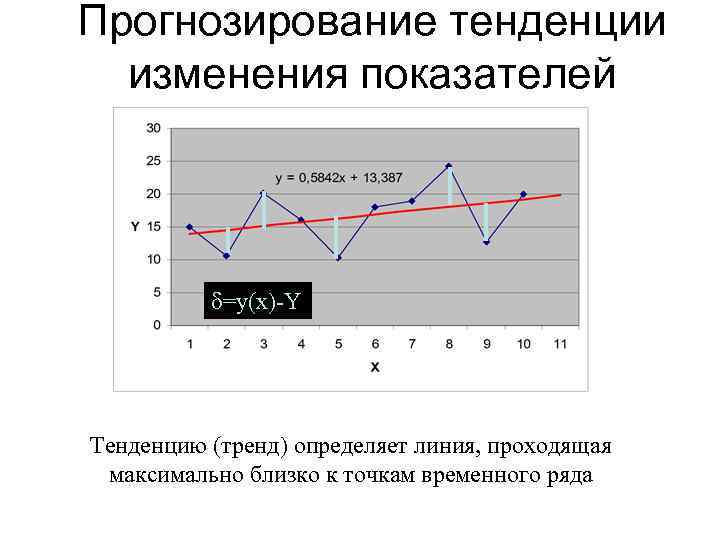Прогнозирование тенденции изменения показателей =y(x)-Y Тенденцию (тренд) определяет линия, проходящая максимально близко к точкам временного ряда

Типовые функции трендов • Линейная • Степенная • Показательная • Экспоненциальная • Гиперболическая • Логарифмическая

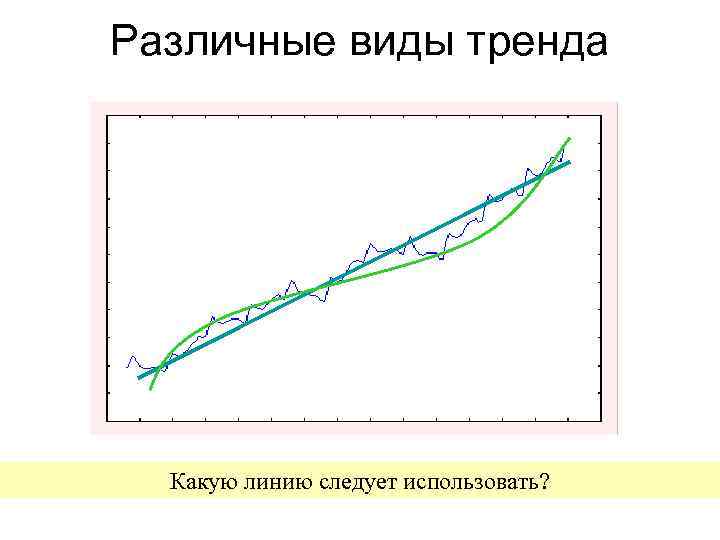Различные виды тренда Какую линию следует использовать?

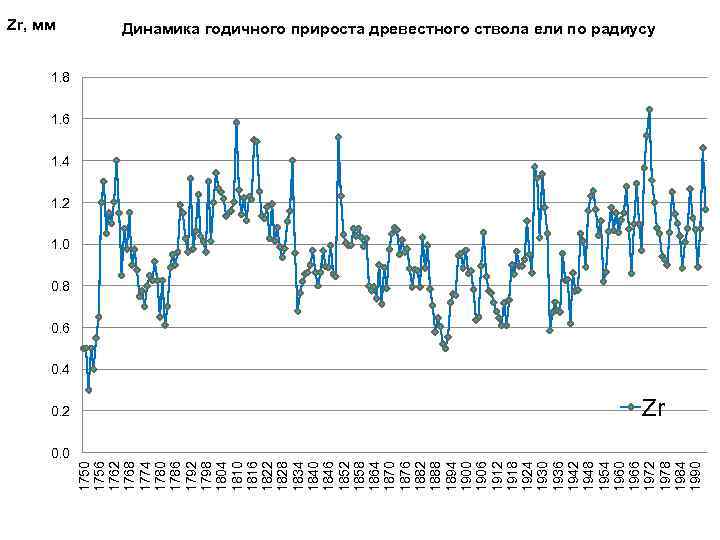0. 2 1750 1756 1762 1768 1774 1780 1786 1792 1798 1804 1810 1816 1822 1828 1834 1840 1846 1852 1858 1864 1870 1876 1882 1888 1894 1900 1906 1912 1918 1924 1930 1936 1942 1948 1954 1960 1966 1972 1978 1984 1990 Zr, мм Динамика годичного прироста древестного ствола ели по радиусу 1. 8 1. 6 1. 4 1. 2 1. 0 0. 8 0. 6 0. 4 Zr 0. 0

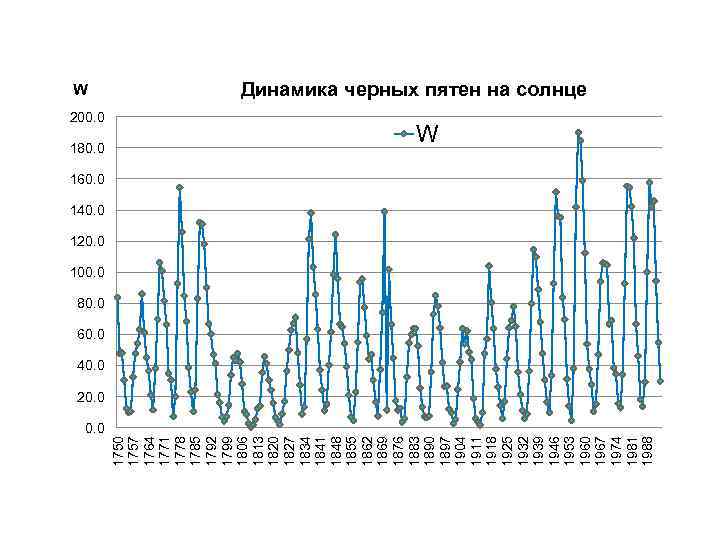200. 0 180. 0 1757 1764 1771 1778 1785 1792 1799 1806 1813 1820 1827 1834 1841 1848 1855 1862 1869 1876 1883 1890 1897 1904 1911 1918 1925 1932 1939 1946 1953 1960 1967 1974 1981 1988 W Динамика черных пятен на солнце W 160. 0 140. 0 120. 0 100. 0 80. 0 60. 0 40. 0 20. 0

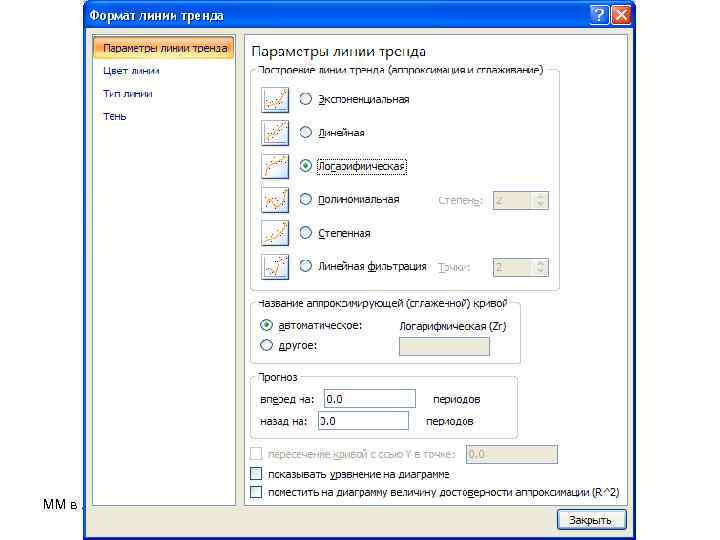ММ в ЛХ

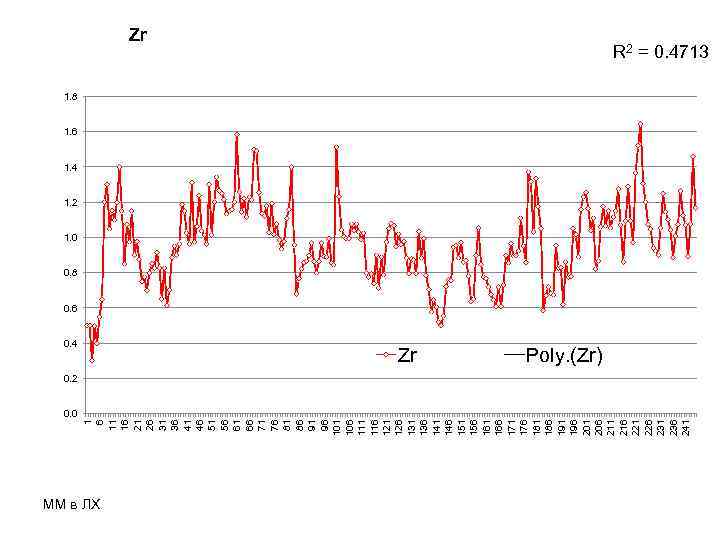0. 0 1 6 11 16 21 26 31 36 41 46 51 56 61 66 71 76 81 86 91 96 101 106 111 116 121 126 131 136 141 146 151 156 161 166 171 176 181 186 191 196 201 206 211 216 221 226 231 236 241 Zr 0. 4 ММ в ЛХ R 2 = 0. 4713 1. 8 1. 6 1. 4 1. 2 1. 0 0. 8 0. 6 Zr Poly. (Zr) 0. 2

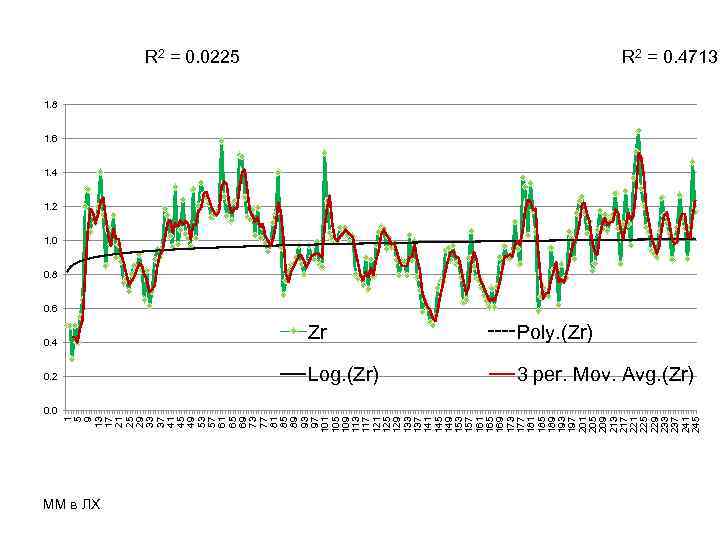0. 0 1 5 9 13 17 21 25 29 33 37 41 45 49 53 57 61 65 69 73 77 81 85 89 93 97 101 105 109 113 117 121 125 129 133 137 141 145 149 153 157 161 165 169 173 177 181 185 189 193 197 201 205 209 213 217 221 225 229 233 237 241 245 R 2 = 0. 0225 0. 4 0. 2 ММ в ЛХ R 2 = 0. 4713 1. 8 1. 6 1. 4 1. 2 1. 0 0. 8 0. 6 Zr Poly. (Zr) Log. (Zr) 3 per. Mov. Avg. (Zr)

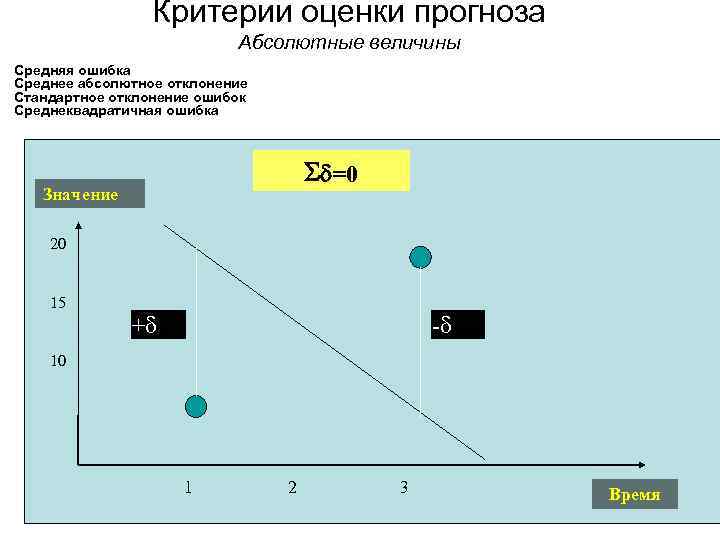Критерии оценки прогноза Абсолютные величины Средняя ошибка Среднее абсолютное отклонение Стандартное отклонение ошибок Среднеквадратичная ошибка =0 Значение 20 15 + - 10 1 2 3 Время

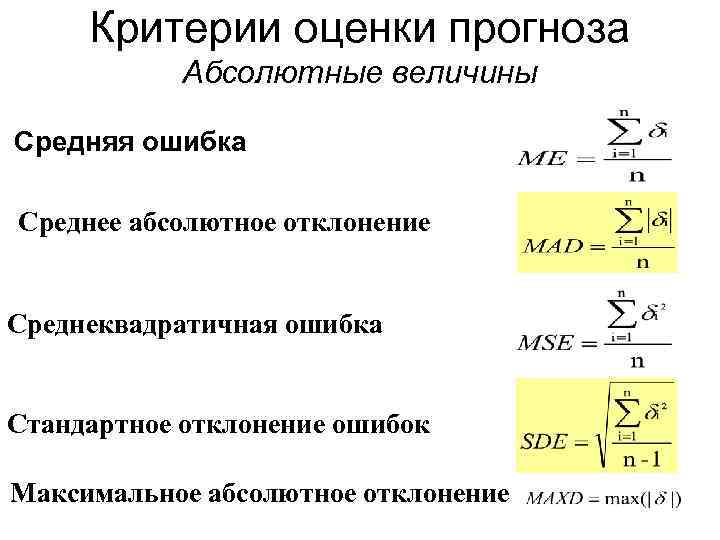Критерии оценки прогноза Абсолютные величины Средняя ошибка Среднее абсолютное отклонение Среднеквадратичная ошибка Стандартное отклонение ошибок Максимальное абсолютное отклонение

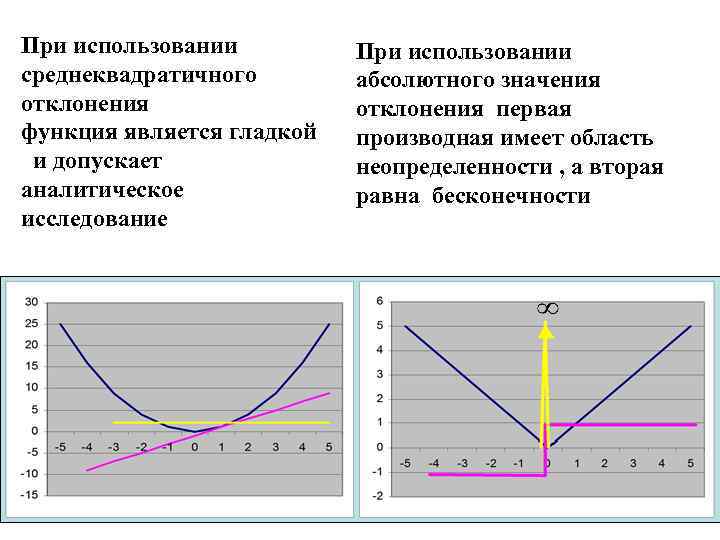При использовании среднеквадратичного отклонения функция является гладкой и допускает аналитическое исследование При использовании абсолютного значения отклонения первая производная имеет область неопределенности , а вторая равна бесконечности Среднеквадратичная ошибка Стандартное отклонение ошибок

Критерии оценки прогноза Относительные величины Процентная ошибка Среднее процентной ошибки Абсолютное среднее процентной ошибки Максимальная процентная ошибка

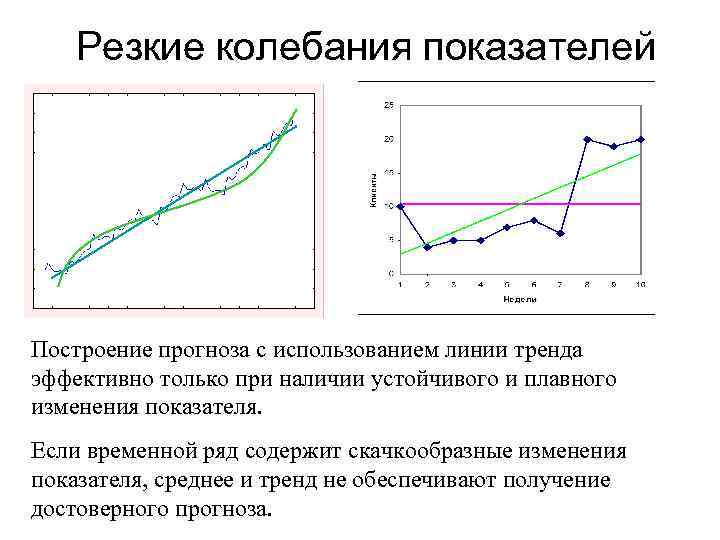Резкие колебания показателей Построение прогноза с использованием линии тренда эффективно только при наличии устойчивого и плавного изменения показателя. Если временной ряд содержит скачкообразные изменения показателя, среднее и тренд не обеспечивают получение достоверного прогноза.

Метод скользящего среднего Используется для построения краткосрочных прогнозов Позволяет: • Учитывать наиболее актуальную (недавнюю) информацию • Оценить погрешность прогноза в процессе его формирования

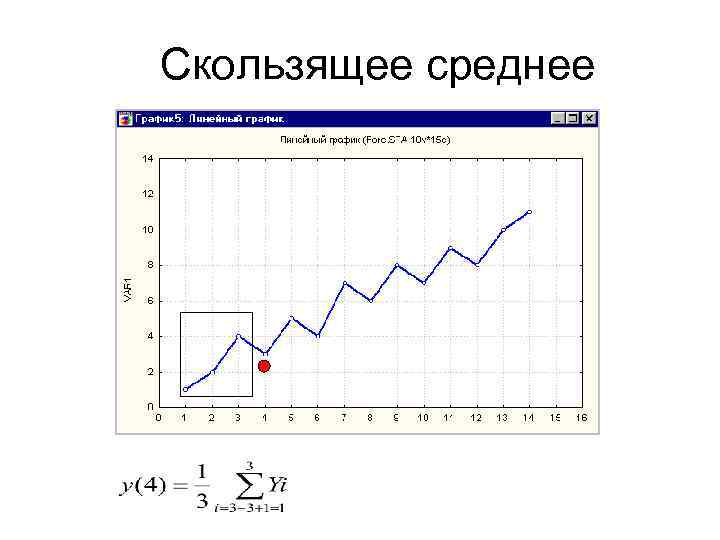Скользящее среднее

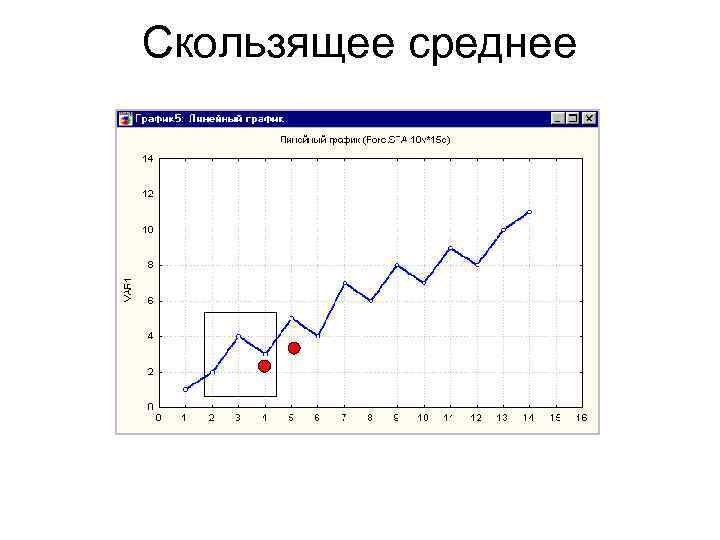Скользящее среднее

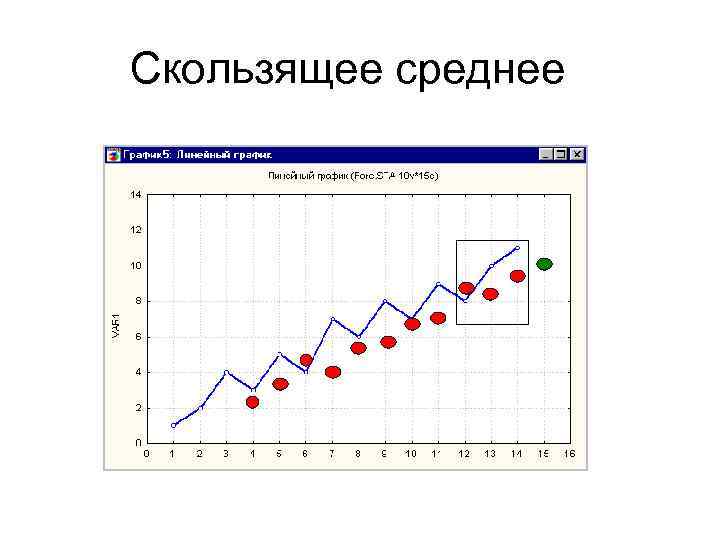Скользящее среднее

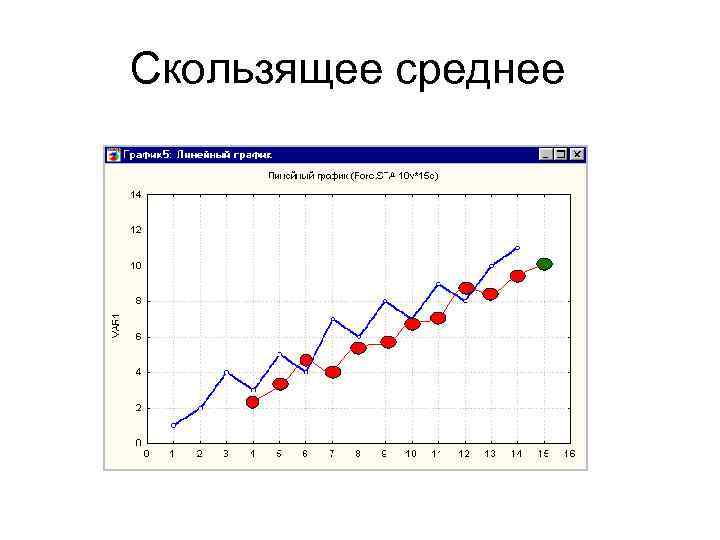Скользящее среднее

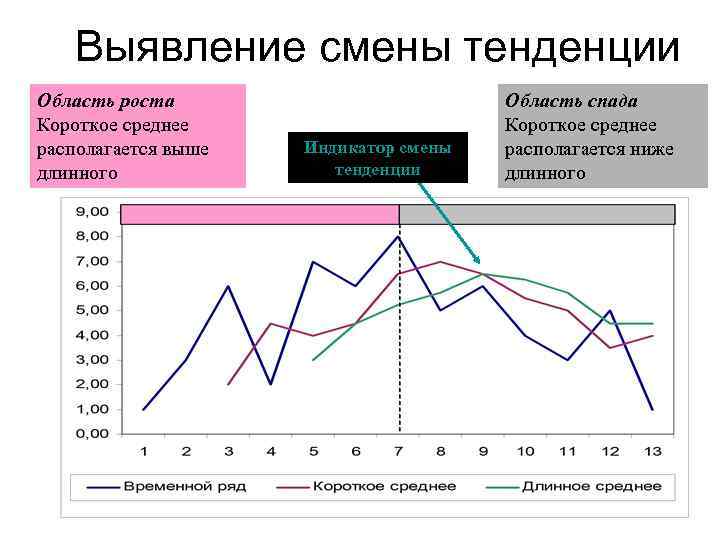Выявление смены тенденции Область роста Короткое среднее располагается выше длинного Индикатор смены тенденции Область спада Короткое среднее располагается ниже длинного

Прогноз для временного ряда с сезонной составляющей К сезонным относят все явления, которые обнаруживают в своем развитии отчетливо выраженную закономерность: устойчиво повторяющиеся колебания уровней (сезонную волну). Последовательность построения прогноза: Определить период сезонной волны Вычислить индексы сезонности Iсез для всех составляющих моментов времени Построить временной ряд, скорректированный с учетом сезонности Yбс = Yфакт : Iсез Построить тренд Yтр Построить прогноз Yпр = Yтр * Iсез

27. 03. 09

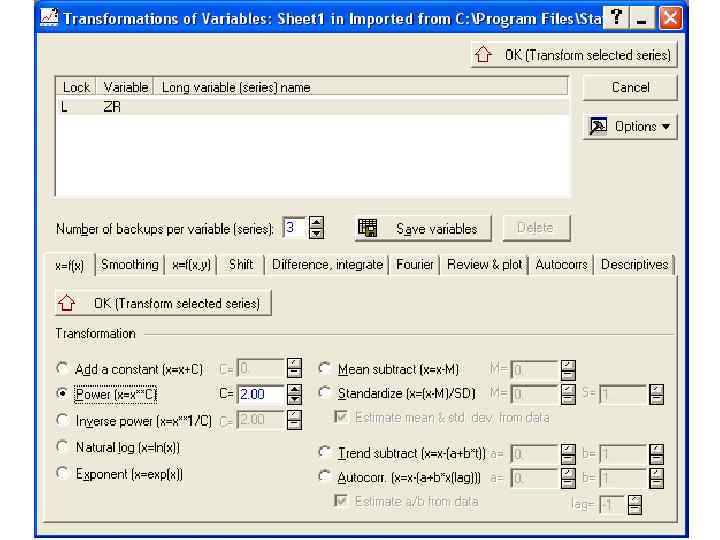
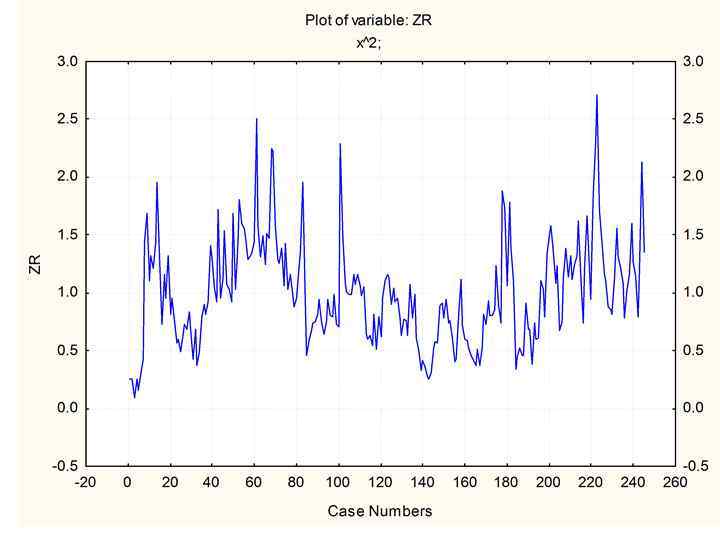
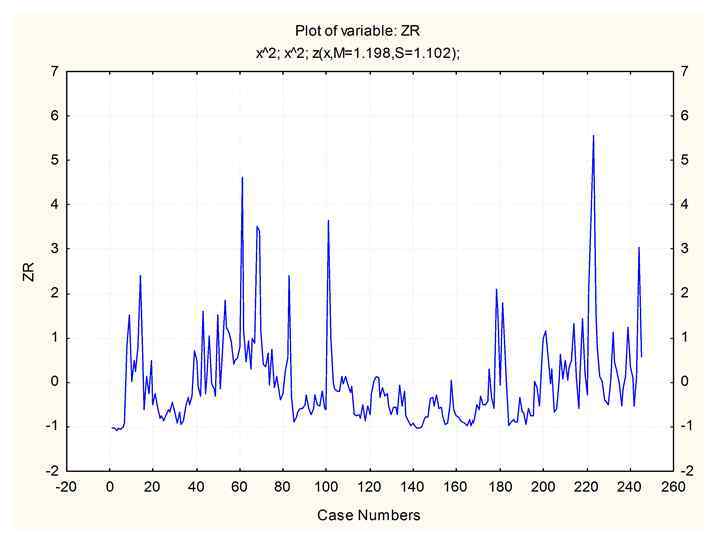
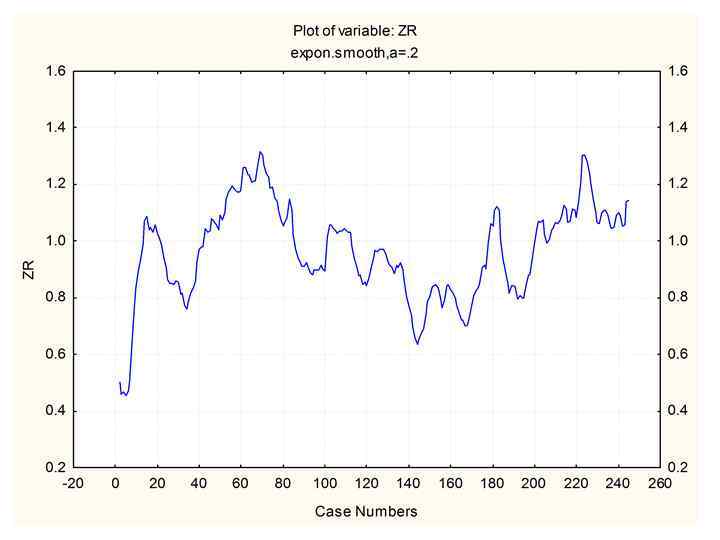
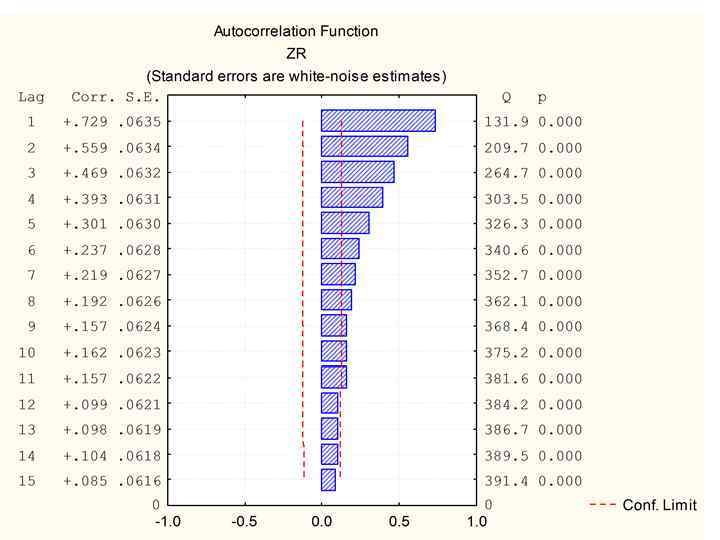
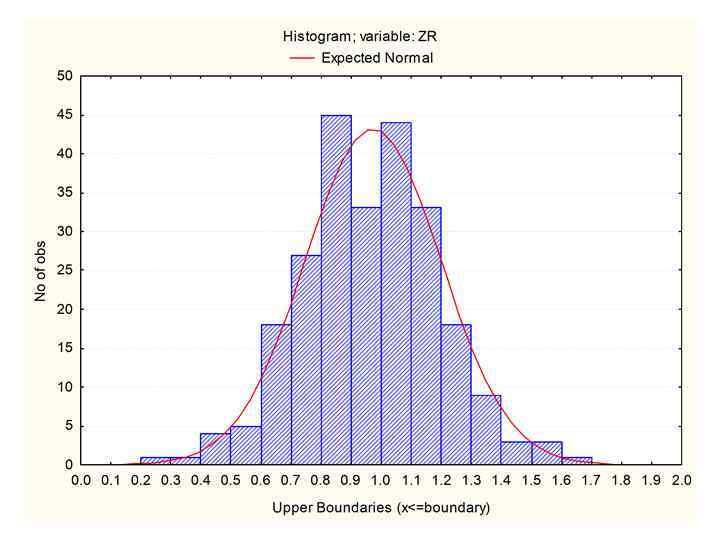
Функции роста • 1) R. Weber (1891): ) G. Mitscherlich : ) F. Korsun (1935): 03. 02. 2018 Таксация 39

Методика автоматизированной разработки таблиц хода роста, моделей актуализации таксационных показателей на естественный рост Модель хода роста древостоя элемента леса принимает вид: где j=1 - индекс высоты, j=2 - индекс диаметра, j=3 - индекс запаса, j=4 - индекс суммы площадей сечения, i=1, 2, 3, . . . , n - индекс возраста с шагом 1, 5 и 10 лет 03. 02. 2018 Таксация Модель изменения параметров роста и формы: 40

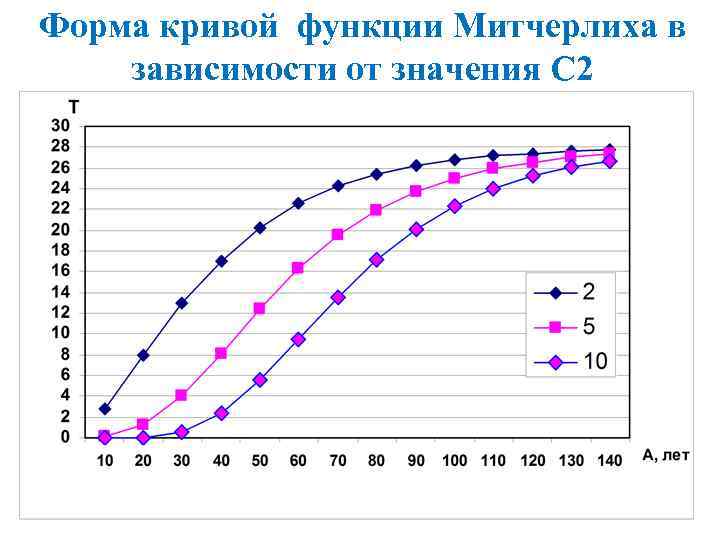Форма кривой функции Митчерлиха в зависимости от значения С 2 03. 02. 2018 Таксация 41

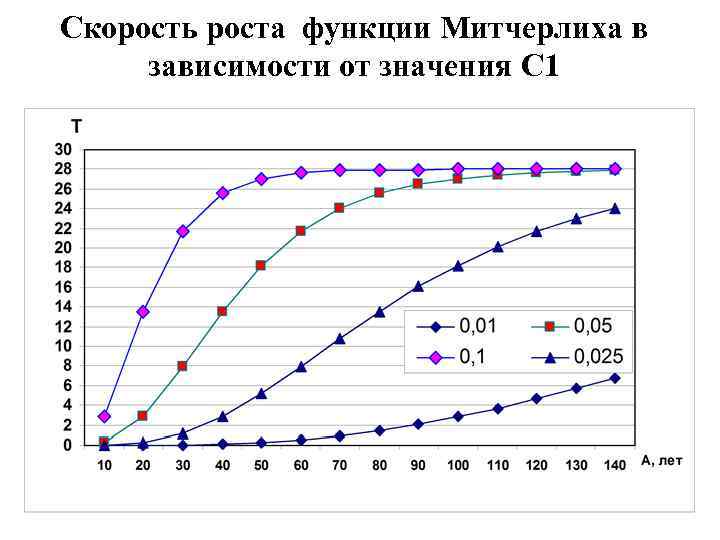Скорость роста функции Митчерлиха в зависимости от значения С 1 03. 02. 2018 Таксация 42

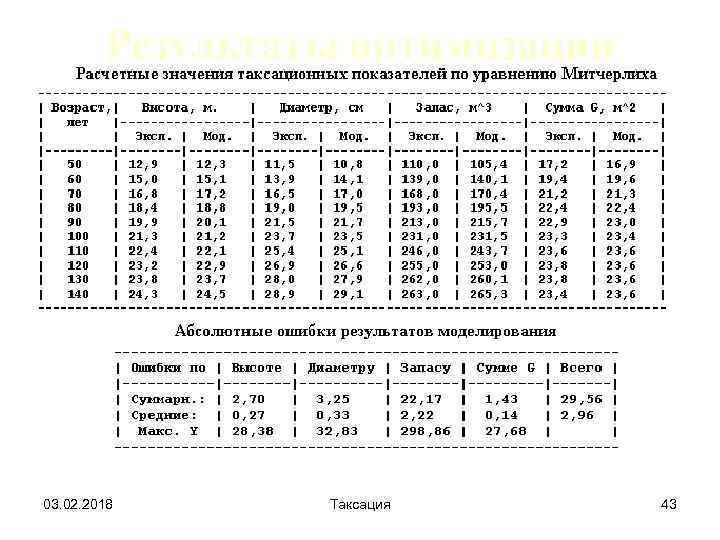Результаты оптимизации таксационных показателей 03. 02. 2018 Таксация 43

Методика автоматизированной разработки таблиц хода роста, моделей актуализации таксационных показателей на естественный рост Модель хода роста древостоя элемента леса принимает вид: где j=1 - индекс высоты, j=2 - индекс диаметра, j=3 - индекс запаса, j=4 - индекс суммы площадей сечения, i=1, 2, 3, . . . , n - индекс возраста с шагом 1, 5 и 10 лет 03. 02. 2018 Таксация Модель изменения параметров роста и формы: 44