Поверхности второго порядка.

Поверхности второго порядка. 1

Определение. Алгебраической поверхностью 2 -го порядка называется поверхность, уравнение которой в Д. П. С. К. можно представить в виде: Ax 2 + By 2 + Cz 2 + Dxy + Exz + Fyz + Gx + Hy + Kz + M = 0, (*) где A 2 + B 2 + C 2 + D 2 + E 2 + F 2 > 0. 2

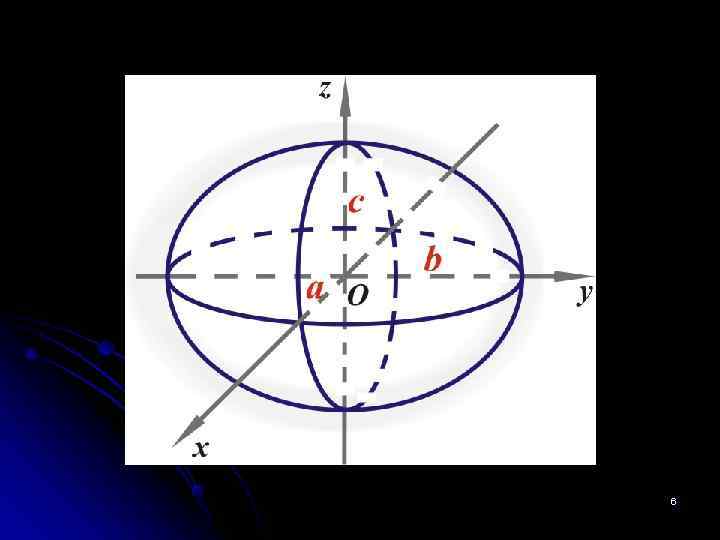
Классификация поверхностей 2 -го порядка. Пусть в Д. П. С. К. задано уравнение второго порядка вида (*). Тогда существует такая Д. П. С. К. ( каноническая), в которой это уравнение примет один из следующих видов (каноническое уравнение): 1. Эллипсоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением Чтобы представить форму эллипсоида и изобразить его на чертеже, применяем метод параллельных сечений. 3

Рассмотрим сечения данного эллипсоида плоскостями, параллельными координатной плоскости XOY. Каждая из таких плоскостей определяется уравнением вида z =h , а линия, которая получается в сечении, определяется двумя уравнениями: Отсюда видно, что 1) при |h| < c плоскость z = h пересекает эллипсоид по эллипсу с полуосями расположенному симметрично относительно осей ОX и ОY. Величины a* и b* имеют наибольшие значения при h=0; иначе говоря, самый крупный эллипс образуется в сечении координатной плоскостью z = 0: 4

При возрастании |h| величины a* и b* убывают, то есть размеры эллипса уменьшаются. 2) при |h| = c плоскость z = h пересекает эллипсоид в точке (0. 0. h), то есть плоскости касаются эллипсоида. 3) при |h| > c плоскость эллипсоид не пересекает. Совершенно аналогичная картина получается при рассмотрении сечений эллипсоида плоскостями, параллельными координатным плоскостям OXZ и OYZ, причем плоскость OXZ пересекает эллипсоид по эллипсу , а плоскость OYZ - по эллипсу Таким образом, эллипсоид является замкнутой овальной поверхностью, обладающей тремя взаимно перпендикулярными осями симметрии. Величины a, b и с 5 называются полуосями эллипсоида.

6

2. Однополостный гиперболоид. Однополостным гиперболоидом называется поверхность, которая в некоторой Д. П. С. К. определяется уравнением 1) Рассмотрим сечения плоскостями, параллельными координатной плоскости XOY: Плоскость z = h пересекает однополостный гиперболоид по эллипсу с полуосями расположенному симметрично относительно плоскостей XOZ и YOZ. 7

Величины a* и b* имеют наименьшие значения при h=0; иначе говоря, самых малых размеров эллипс образуется в сечении координатной плоскостью z = 0: (он называется горловым эллипсом). При возрастании |h| величины a* и b* возрастают , то есть размеры эллипса увеличиваются. 2)Сечение плоскостью OXZ определяется уравнениями: Данное сечение представляет собой гиперболу, расположенную симметрично относительно координатных осей OX и OZ и пересекающую ось OX в точках (a; 0; 0) и (-a; 0; 0). 8

Рассмотрим сечение гиперболоида плоскостями, параллельными координатной плоскости OXZ : При |h| = b – пара пересекающихся прямых При |h| = b гипербола: |h| < b: |h| > b: 9

3)Сечение плоскостью OYZ: Данное сечение представляет собой гиперболу, расположенную симметрично относительно координатных осей OY и OZ и пересекающую ось OY в точках (0; b; 0) и (0; -b; 0). Сечение плоскостями, параллельными координатной плоскости OYZ. При |h| = a – пара пересекающихся прямых при - гипербола, |h| < a: |h| >a: 10

Таким образом, однополостный гиперболоид имеет вид бесконечной трубки, бесконечно расширяющейся в обе стороны от горлового эллипса. 11

3. Двуполостный гиперболоид. Двуполостным гиперболоидом называется поверхность, которая в некоторой Д. П. С. К. определяется уравнением Рассмотрим сечения данного двуполостного гиперболоида плоскостями, параллельными координатной плоскости XOY. Отсюда видно, что 1) При |h| > с плоскость пересекает двуполостный гиперболоид по эллипсу с полуосями расположенному симметрично 12 относительно плоскостей XOZ и YOZ.

При возрастании |h| величины a* и b* и возрастают, то есть размеры эллипса увеличиваются. Если | h| , убывая, приближается к с, то полуоси эллипса также убывают и приближаются к нулю. 2) при |h| = с плоскость z = h пересекает двуполостный гиперболоид в точке (0. 0. h), то есть плоскости касаются гиперболоида. 3) при |h| < c плоскость гиперболоид не пересекает. Сечение плоскостью OXZ определяется уравнениями: Данное сечение представляет собой гиперболу, расположенную симметрично относительно координатных осей OX и OZ и пересекающую ось OZ в 13 точках (0; 0; с) и (0; 0; -с).

В сечении гиперболоида плоскостями, параллельными координатной плоскости OXZ - гипербола. Сечение плоскостью OYZ определяется уравнениями: Данное сечение представляет собой гиперболу, расположенную симметрично относительно координатных осей OY и OZ и пересекающую ось OZ в точках (0; 0; с) и (0; 0; -с). 14

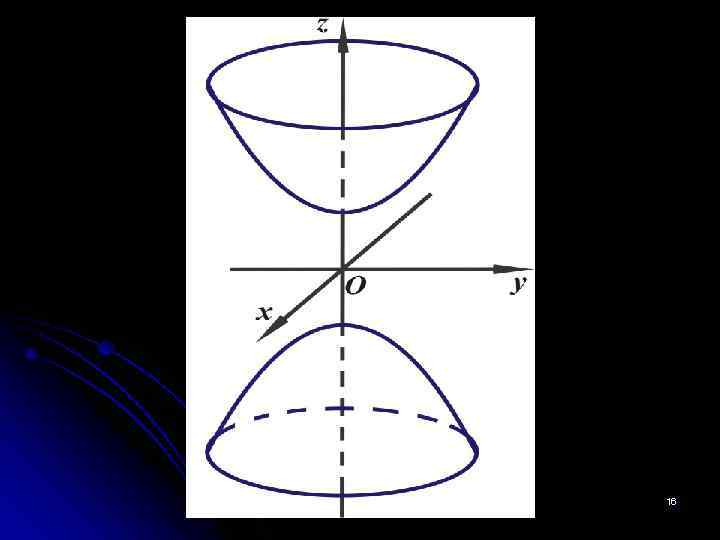
В сечении гиперболоида плоскостями, параллельными координатной плоскости OYZ – гипенрбола: Таким образом, двуполостный гиперболоид есть поверхность, состоящая из двух отдельных «полостей» ; каждая из них имеет вид бесконечной выпуклой чаши. Двуполостный гиперболоид обладает тремя взаимно перпендикулярными плоскостями симметрии. 15

16

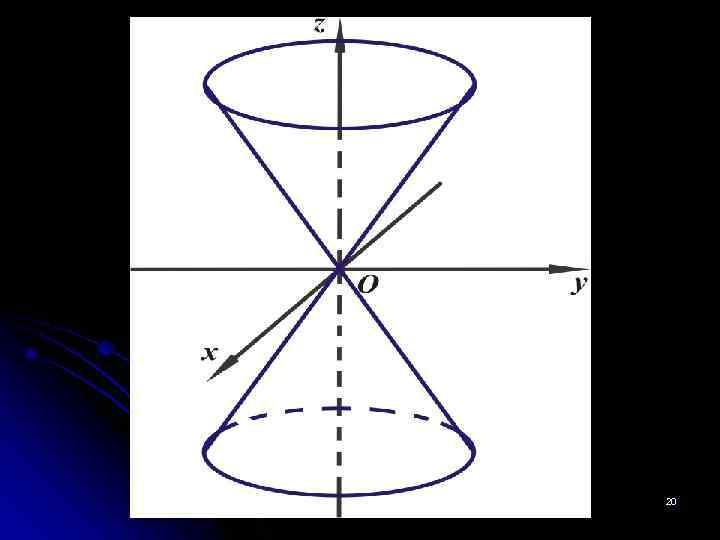
4. Конус второго порядка. Конусом второго порядка называется поверхность, которая в некоторой Д. П. С. К. определяется уравнением Особенность данного уравнения состоит в том, что оно однородно, то есть все его члены имеют одну и ту же степень. Любая поверхность, определяемая однородным уравнением, состоит из прямых, проходящих через начало координат. Если некоторая точка M (отличная от начала координат) лежит на этой поверхности, то все точки прямой, которая проходит через начало координат и точку M, также лежат на этой поверхности. Такая поверхность называется конической. Прямые, из которых составлен конус, называются его образующими, точка, через 17 которую все они проходят, называется вершиной конуса.

Рассмотрим сечения конуса плоскостями, параллельными координатной плоскости XOY: Плоскость z=h пересекает конус по эллипсу с полуосями , расположенному симметрично относительно плоскостей XOZ и YOZ. Если |h| , убывая, приближается к 0, то полуоси эллипса также убывают и приближаются к нулю. При возрастании |h| величины a* и b* возрастают, то есть размеры эллипса увеличиваются. При h=0, в сечении получается точка (0, 0, 0). 18

В сечении конуса плоскостями, параллельными координатной плоскости OXZ (0 YZ) гипербола при и пара пересекающихся прямых при h=0 . 19

20

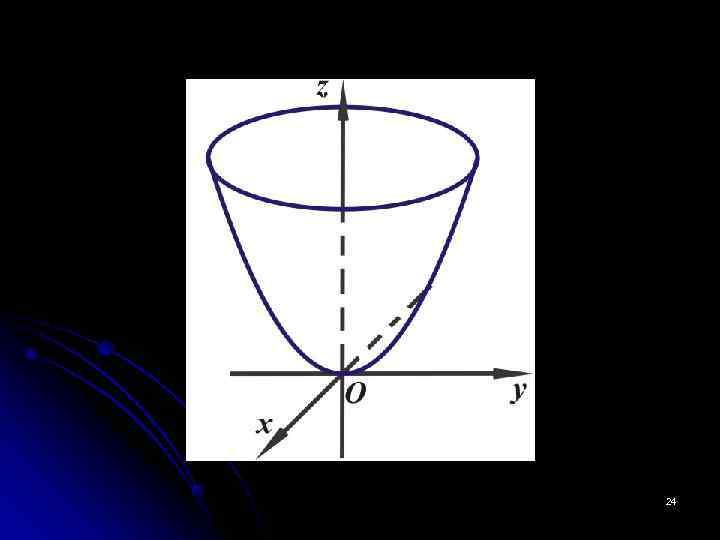
5. Эллиптический параболоид. Эллиптическим параболоидом называется поверхность, которая в некоторой Д. П. С. К. определяется уравнением Сечение плоскостью OXZ : парабола, симметричная относительно оси OZ, с вершиной в начале координат. В сечении параболоида плоскостями, параллельными координатной плоскости OXZ: – парабола с вершиной в точке x=0, 21

Сечение плоскостью OYZ : - парабола, расположенная симметрично относительно оси OZ, с вершиной в начале координат. В сечении параболоида плоскостями, параллельными координатной плоскости OYZ : – парабола с вершиной в точке y=0, Сечения эллиптического параболоида плоскостями, параллельными координатной плоскости XOY: Отсюда видно, что плоскость z=h при h>0 пересекает эллиптический параболоид по эллипсу с полуосями расположенному симметрично относительно плоскостей XOZ и YOZ. 22

Если |h|, убывая, приближается к 0, то полуоси эллипса также убывают и приближаются к нулю При возрастании |h| величины a* и b* возрастают, то есть размеры эллипса увеличиваются. При h=0 эллипс вырождается в точку. При h<0 плоскость и параболоид не пересекаются. Следовательно, эллиптический параболоид имеет вид бесконечной выпуклой чаши. Он обладает двумя взаимно перпендикулярными плоскостями симметрии. 23

24

6. Гиперболический параболоид. Гиперболическим параболоидом называется поверхность, которая в некоторой Д. П. С. К. определяется уравнением: Сечение плоскостью OXZ : представляет собой параболу, расположенную симметрично относительно оси OZ, с вершиной в начале координат. В сечении параболоида плоскостями, параллельными координатной плоскости OXZ: парабола с вершиной в точке x=0, 25

Сечение плоскостью OYZ : представляет собой параболу, расположенную симметрично относительно оси OZ, с вершиной в начале координат. В сечении параболоида плоскостями, параллельными координатной плоскости OYZ : парабола с вершиной в точке y =0, 26

Рассмотрим сечения гиперболического параболоида плоскостями, параллельными координатной плоскости XOY. Плоскости z=h пересекают гиперболический параболоид по гиперболам, расположенным симметрично относительно плоскостей XOZ и YOZ. Если h>0, то гипербола пересекает плоскость OXZ, если h<0 - гипербола пересекает плоскость OYZ. h>0 h<0 27

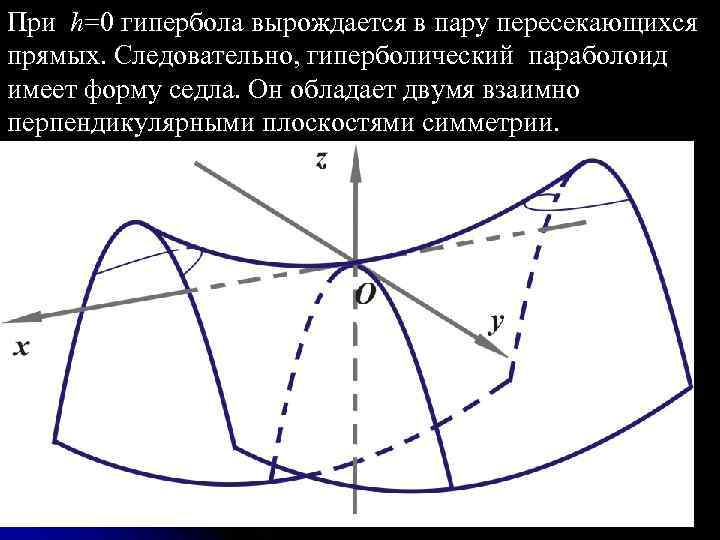
При h=0 гипербола вырождается в пару пересекающихся прямых. Следовательно, гиперболический параболоид имеет форму седла. Он обладает двумя взаимно перпендикулярными плоскостями симметрии. 28

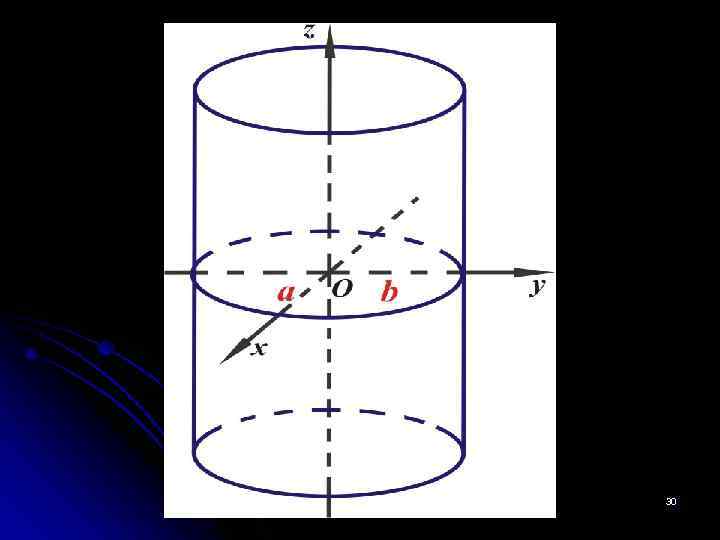
7. Эллиптический цилиндр второго порядка. Эллиптическим цилиндром называется поверхность, которая в некоторой Д. П. С. К. определяется уравнением Сечения плоскостями, параллельными координатной плоскости XOY: Отсюда видно, что при любом h плоскость пересекает эллиптический цилиндр по эллипсу с полуосями a и b, расположенному симметрично относительно осей ОX и ОY. 29

30

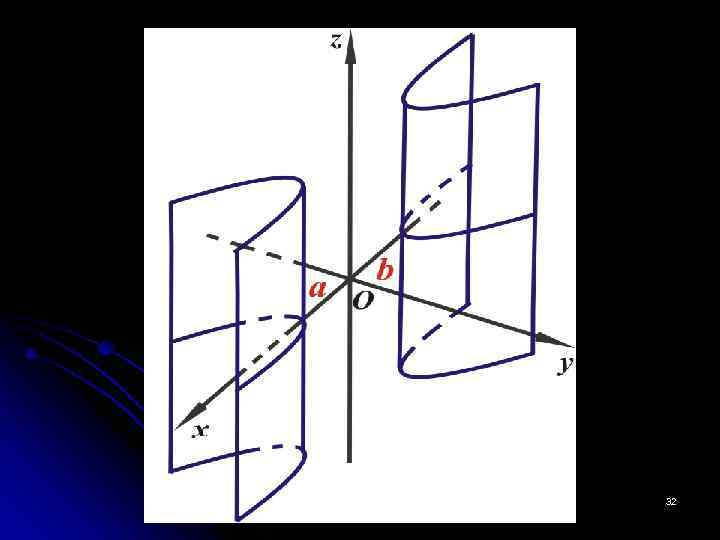
8. Гиперболический цилиндр второго порядка Гиперболическим цилиндром называется поверхность, которая в некоторой Д. П. С. К. определяется уравнением В сечении плоскостями, параллельными координатной плоскости XOY: При любом h плоскость пересекает гиперболический цилиндр по гиперболе, расположенной симметрично относительно осей ОX и ОY. 31

32

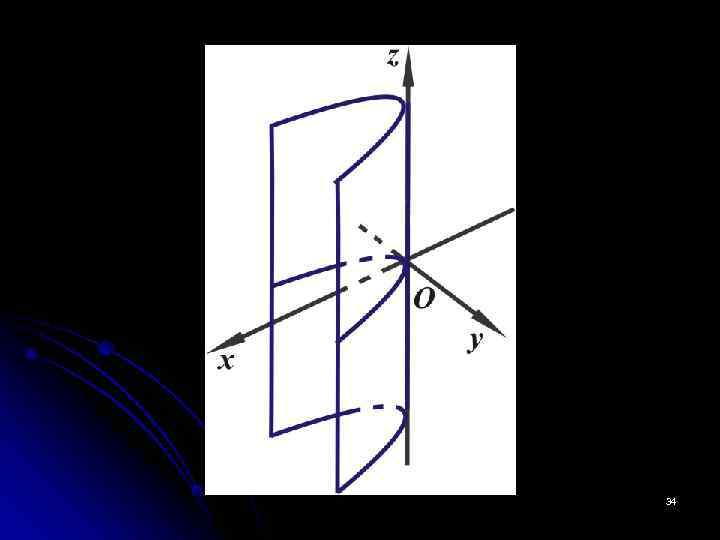
9. Параболический цилиндр второго порядка. Параболическим цилиндром называется поверхность, которая в некоторой Д. П. С. К. определяется уравнением y 2 = 2 px. В сечении плоскостями, параллельными координатной плоскости XOY При любом h плоскость пересекает параболический цилиндр по параболе, расположенной симметрично относительно оси ОX. 33

34

10. Мнимый эллипсоид (не определяет никакого действительного образа) – 11. Пара пересекающихся плоскостей – где bx ay = 0 – уравнения плоскостей. 12. Точка (0, 0, 0). 13. прямая, совпадающая с осью OZ. 35

14. - параллельных плоскостей. 15. - пара совпадающих параллельных плоскостей. 16. - пара мнимых плоскостей. 17. (не определяет никакого действительного образа). 36