Поверхность в проекциях с числовыми отметками задаются своими

Поверхность в проекциях с числовыми отметками задаются своими горизонталями. Горизонтали поверхности можно представить как линии сечения этих поверхностей горизонтальными плоскостями, проведенными с постоянным шагом. Построение таких горизонталей является задачей градуировки поверхности. Линия ската применительно к поверхностям обычно рассматривается для конкретной точки и проводится перпендикулярно горизонталям, проходящим через нее.

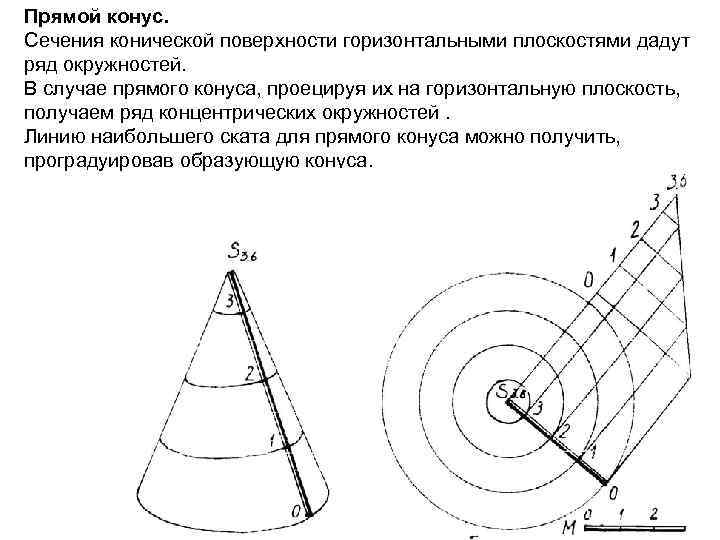Прямой конус. Сечения конической поверхности горизонтальными плоскостями дадут ряд окружностей. В случае прямого конуса, проецируя их на горизонтальную плоскость, получаем ряд концентрических окружностей. Линию наибольшего ската для прямого конуса можно получить, проградуировав образующую конуса.

Конус наклонный. Центры окружностей, получаемых при его рассечении параллельными плоскостями, не лежат на одной вертикальной оси. Для градуирования наклонного конуса градуируют его самую длинную и самую короткую образующую. Находят на образующих точки с одинаковыми отметками, они отмечают диаметр окружности являющейся горизонталью. Для отыскания центра этой окружности можно воспользоваться делением отрезка (диаметра) на две равные части или провести ось вертикальной проекции конуса, которой эти центры окружностей принадлежат.

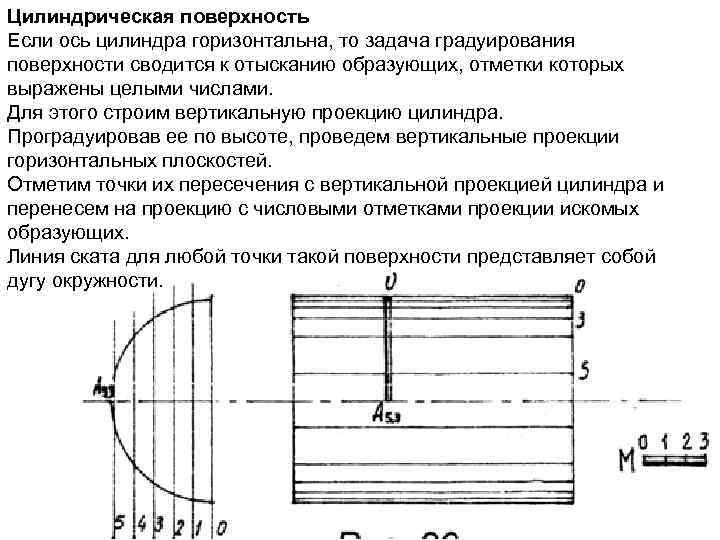Цилиндрическая поверхность Если ось цилиндра горизонтальна, то задача градуирования поверхности сводится к отысканию образующих, отметки которых выражены целыми числами. Для этого строим вертикальную проекцию цилиндра. Проградуировав ее по высоте, проведем вертикальные проекции горизонтальных плоскостей. Отметим точки их пересечения с вертикальной проекцией цилиндра и перенесем на проекцию с числовыми отметками проекции искомых образующих. Линия ската для любой точки такой поверхности представляет собой дугу окружности.

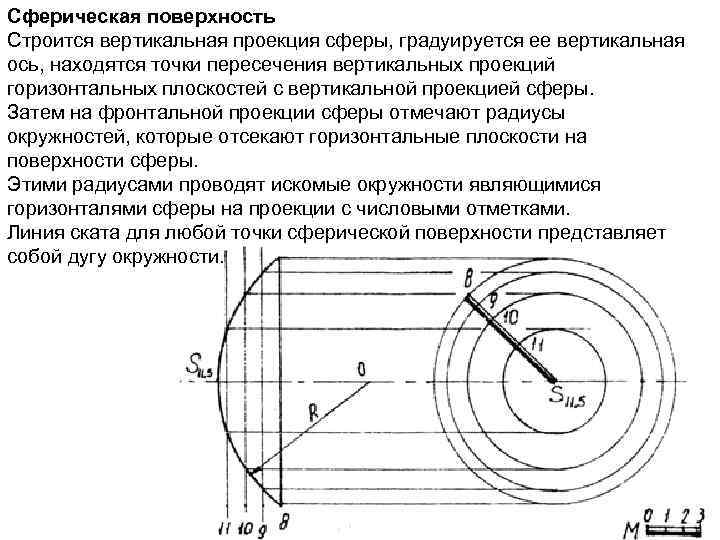Сферическая поверхность Строится вертикальная проекция сферы, градуируется ее вертикальная ось, находятся точки пересечения вертикальных проекций горизонтальных плоскостей с вертикальной проекцией сферы. Затем на фронтальной проекции сферы отмечают радиусы окружностей, которые отсекают горизонтальные плоскости на поверхности сферы. Этими радиусами проводят искомые окружности являющимися горизонталями сферы на проекции с числовыми отметками. Линия ската для любой точки сферической поверхности представляет собой дугу окружности.

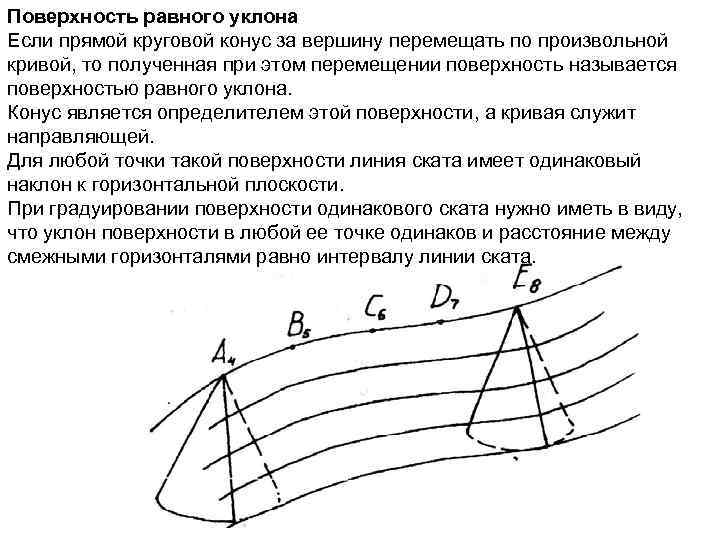Поверхность равного уклона Если прямой круговой конус за вершину перемещать по произвольной кривой, то полученная при этом перемещении поверхность называется поверхностью равного уклона. Конус является определителем этой поверхности, а кривая служит направляющей. Для любой точки такой поверхности линия ската имеет одинаковый наклон к горизонтальной плоскости. При градуировании поверхности одинакового ската нужно иметь в виду, что уклон поверхности в любой ее точке одинаков и расстояние между смежными горизонталями равно интервалу линии ската.

Для градуирования размещаем конусы в точках заданной направляющей кривой и градуируем их поверхности. На практике это выглядит как проведение из точек кривой концентрических окружностей, радиусы которых отличаются на величину интервала, а высотные отметки на единицу. Проведя кривые линии, соприкасающиеся с этими горизонталями конических поверхностей, имеющих одну и ту же отметку, получим горизонтали поверхности равного уклона.

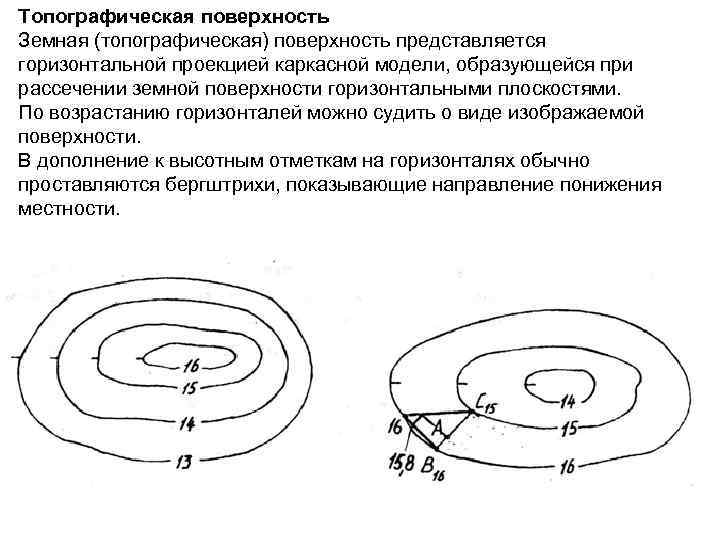Топографическая поверхность Земная (топографическая) поверхность представляется горизонтальной проекцией каркасной модели, образующейся при рассечении земной поверхности горизонтальными плоскостями. По возрастанию горизонталей можно судить о виде изображаемой поверхности. В дополнение к высотным отметкам на горизонталях обычно проставляются бергштрихи, показывающие направление понижения местности.

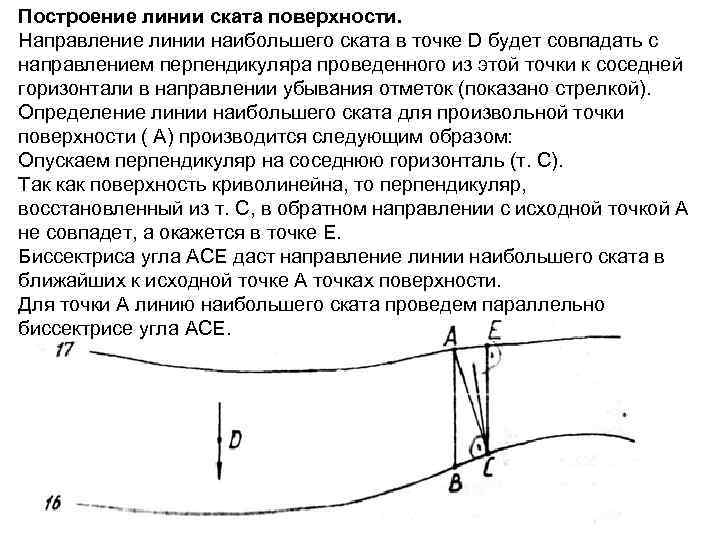Построение линии ската поверхности. Направление линии наибольшего ската в точке D будет совпадать с направлением перпендикуляра проведенного из этой точки к соседней горизонтали в направлении убывания отметок (показано стрелкой). Определение линии наибольшего ската для произвольной точки поверхности ( A) производится следующим образом: Опускаем перпендикуляр на соседнюю горизонталь (т. C). Так как поверхность криволинейна, то перпендикуляр, восстановленный из т. C, в обратном направлении с исходной точкой A не совпадет, а окажется в точке E. Биссектриса угла ACE даст направление линии наибольшего ската в ближайших к исходной точке A точках поверхности. Для точки A линию наибольшего ската проведем параллельно биссектрисе угла ACE.

Определить линию сечения топографической поверхности проецирующей плоскостью. Такое сечение называется профилем поверхности. Секущая плоскость задана своей горизонтальной проекцией γ. Отметив точки пересечения плоскости с горизонталями поверхности, построим профиль поверхности. Для этого выберем базовую горизонталь соответствующую, или несколько ниже, минимальной отметке горизонтали местности, пересекаемой плоскостью γ.

Проводим перпендикулярно следу плоскости линии связи, отложим на них отметки соответствующих горизонталей и соединим их плавной кривой. На профиль наносится сетка горизонталей. Первая горизонталь профиля называется базовой. Профиль может быть наложенным или вынесенным.

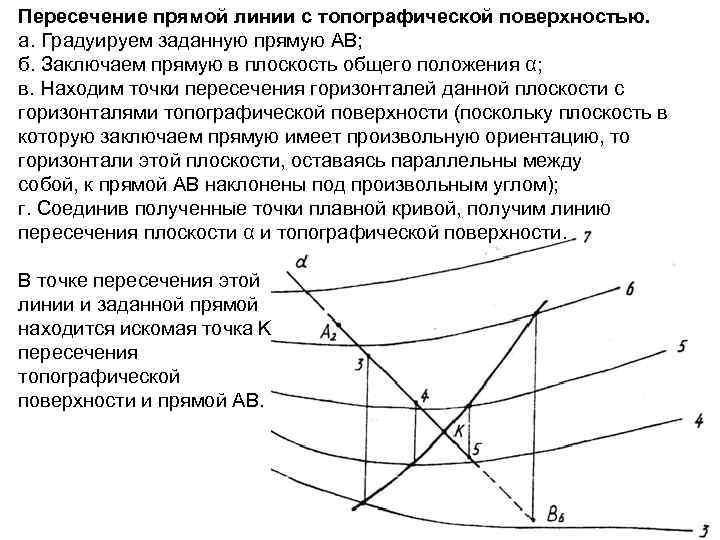Пересечение прямой линии с топографической поверхностью. а. Градуируем заданную прямую AB; б. Заключаем прямую в плоскость общего положения α; в. Находим точки пересечения горизонталей данной плоскости с горизонталями топографической поверхности (поскольку плоскость в которую заключаем прямую имеет произвольную ориентацию, то горизонтали этой плоскости, оставаясь параллельны между собой, к прямой AB наклонены под произвольным углом); г. Соединив полученные точки плавной кривой, получим линию пересечения плоскости α и топографической поверхности. В точке пересечения этой линии и заданной прямой находится искомая точка K пересечения топографической поверхности и прямой AB.

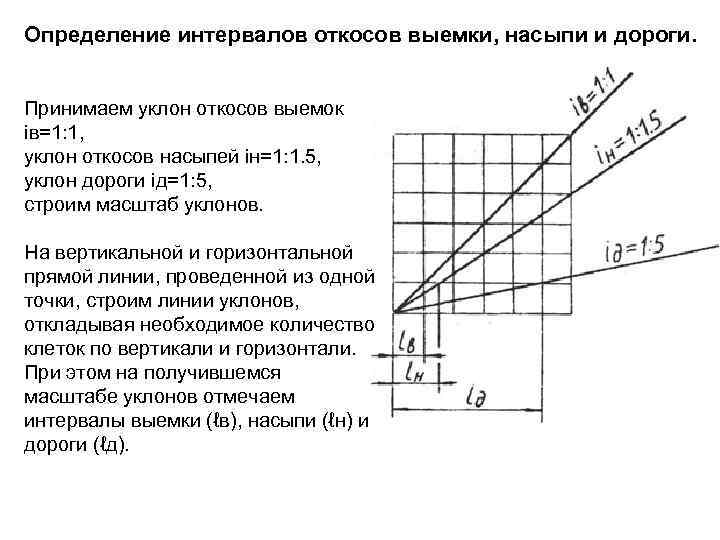Определение интервалов откосов выемки, насыпи и дороги. Принимаем уклон откосов выемок iв=1: 1, уклон откосов насыпей iн=1: 1. 5, уклон дороги iд=1: 5, строим масштаб уклонов. На вертикальной и горизонтальной прямой линии, проведенной из одной точки, строим линии уклонов, откладывая необходимое количество клеток по вертикали и горизонтали. При этом на получившемся масштабе уклонов отмечаем интервалы выемки (ℓв), насыпи (ℓн) и дороги (ℓд).

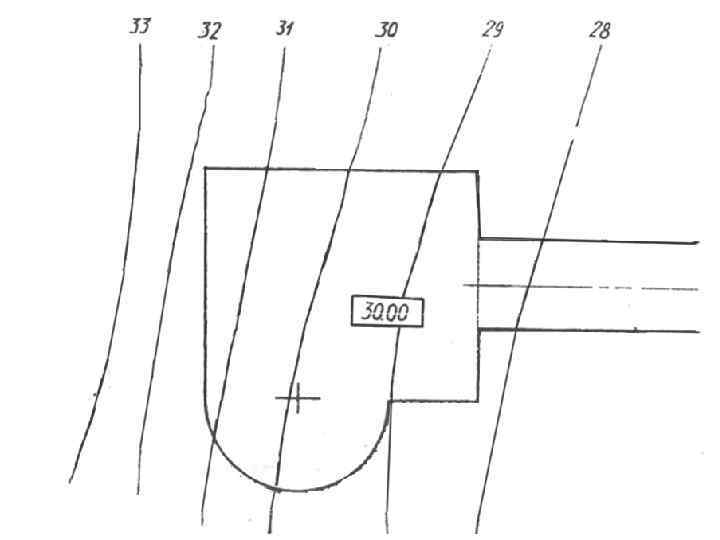
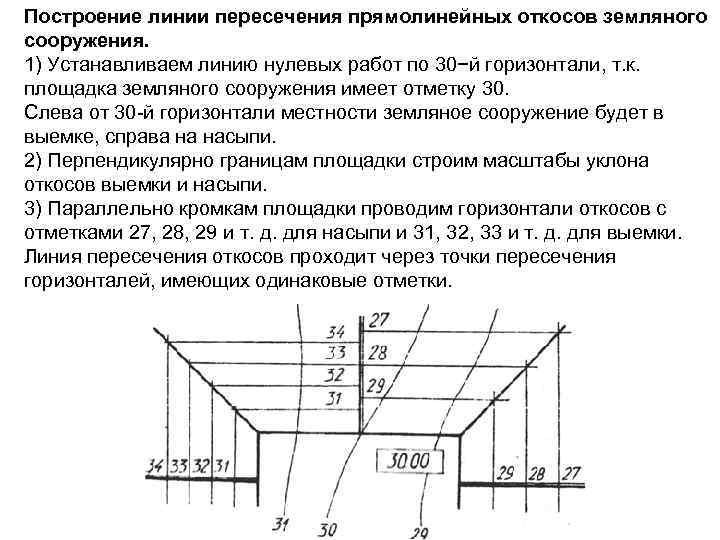Построение линии пересечения прямолинейных откосов земляного сооружения. 1) Устанавливаем линию нулевых работ по 30−й горизонтали, т. к. площадка земляного сооружения имеет отметку 30. Слева от 30 -й горизонтали местности земляное сооружение будет в выемке, справа на насыпи. 2) Перпендикулярно границам площадки строим масштабы уклона откосов выемки и насыпи. 3) Параллельно кромкам площадки проводим горизонтали откосов с отметками 27, 28, 29 и т. д. для насыпи и 31, 32, 33 и т. д. для выемки. Линия пересечения откосов проходит через точки пересечения горизонталей, имеющих одинаковые отметки.

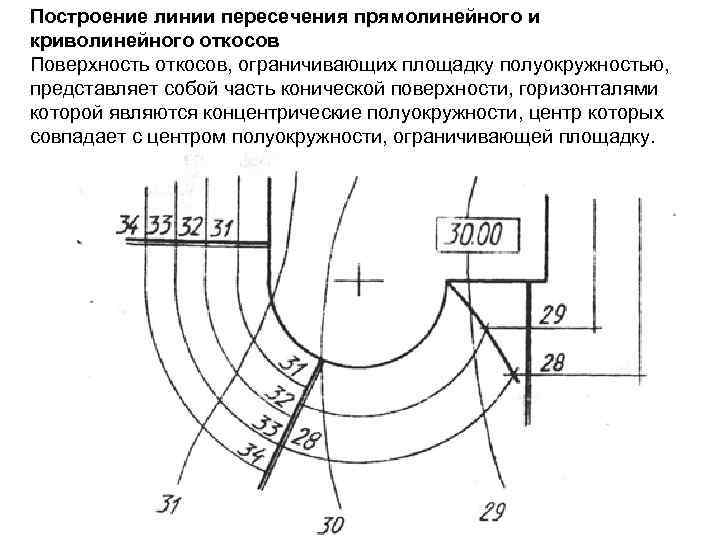Построение линии пересечения прямолинейного и криволинейного откосов Поверхность откосов, ограничивающих площадку полуокружностью, представляет собой часть конической поверхности, горизонталями которой являются концентрические полуокружности, центр которых совпадает с центром полуокружности, ограничивающей площадку.

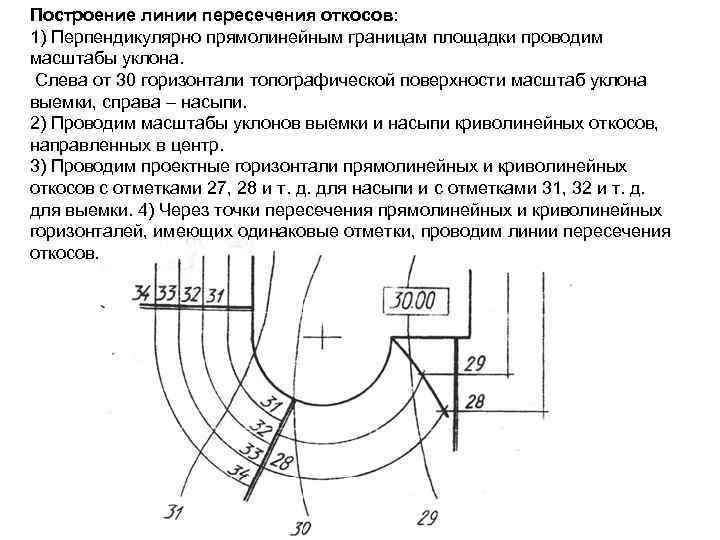Построение линии пересечения откосов: 1) Перпендикулярно прямолинейным границам площадки проводим масштабы уклона. Слева от 30 горизонтали топографической поверхности масштаб уклона выемки, справа – насыпи. 2) Проводим масштабы уклонов выемки и насыпи криволинейных откосов, направленных в центр. 3) Проводим проектные горизонтали прямолинейных и криволинейных откосов с отметками 27, 28 и т. д. для насыпи и с отметками 31, 32 и т. д. для выемки. 4) Через точки пересечения прямолинейных и криволинейных горизонталей, имеющих одинаковые отметки, проводим линии пересечения откосов.

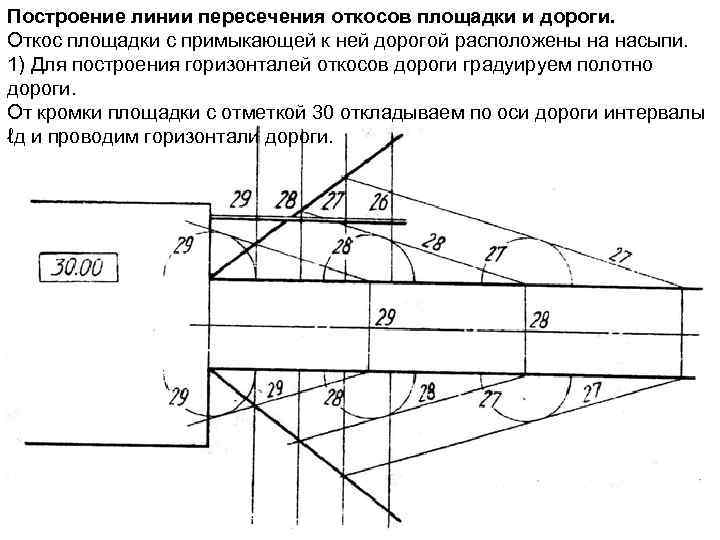Построение линии пересечения откосов площадки и дороги. Откос площадки с примыкающей к ней дорогой расположены на насыпи. 1) Для построения горизонталей откосов дороги градуируем полотно дороги. От кромки площадки с отметкой 30 откладываем по оси дороги интервалы ℓд и проводим горизонтали дороги.

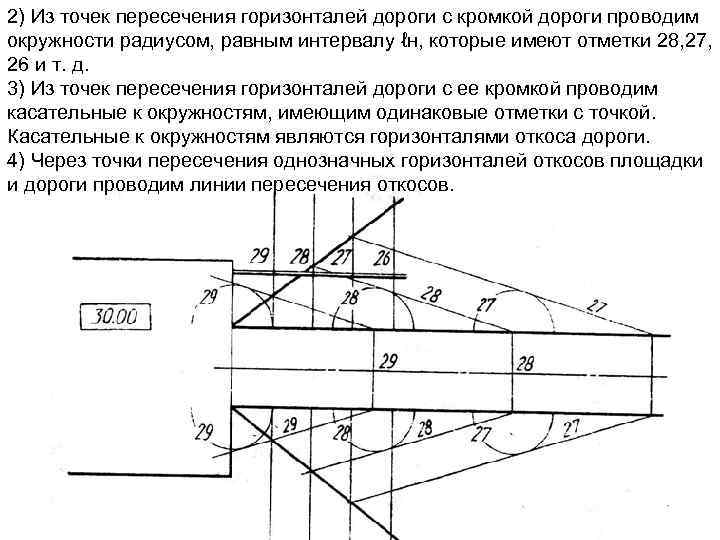2) Из точек пересечения горизонталей дороги с кромкой дороги проводим окружности радиусом, равным интервалу ℓн, которые имеют отметки 28, 27, 26 и т. д. 3) Из точек пересечения горизонталей дороги с ее кромкой проводим касательные к окружностям, имеющим одинаковые отметки с точкой. Касательные к окружностям являются горизонталями откоса дороги. 4) Через точки пересечения однозначных горизонталей откосов площадки и дороги проводим линии пересечения откосов.

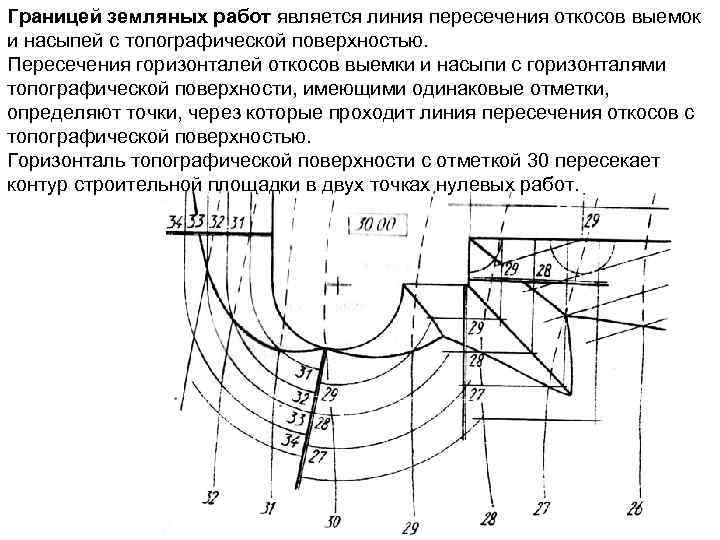Границей земляных работ является линия пересечения откосов выемок и насыпей с топографической поверхностью. Пересечения горизонталей откосов выемки и насыпи с горизонталями топографической поверхности, имеющими одинаковые отметки, определяют точки, через которые проходит линия пересечения откосов с топографической поверхностью. Горизонталь топографической поверхности с отметкой 30 пересекает контур строительной площадки в двух точках нулевых работ.

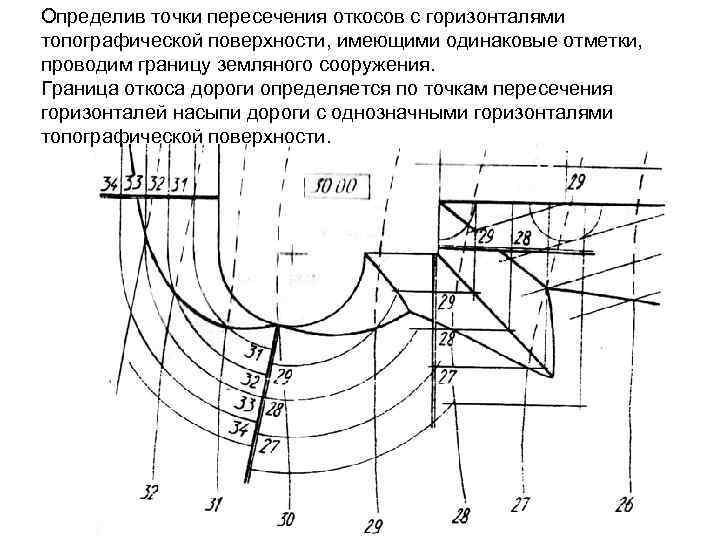Определив точки пересечения откосов с горизонталями топографической поверхности, имеющими одинаковые отметки, проводим границу земляного сооружения. Граница откоса дороги определяется по точкам пересечения горизонталей насыпи дороги с однозначными горизонталями топографической поверхности.

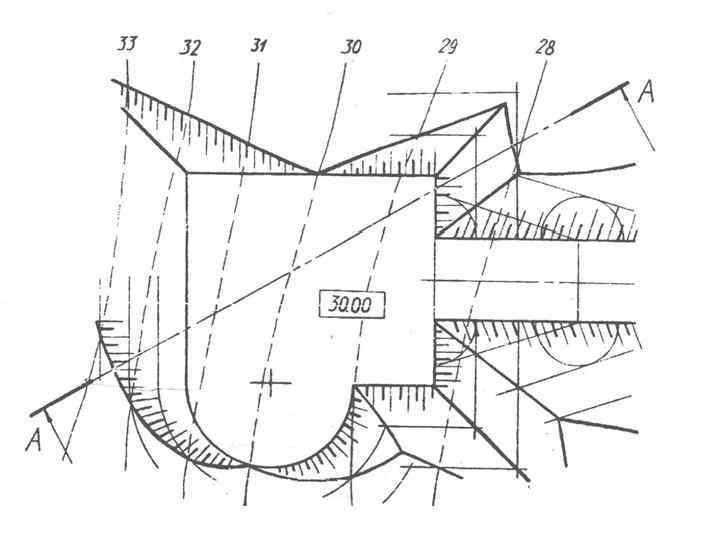
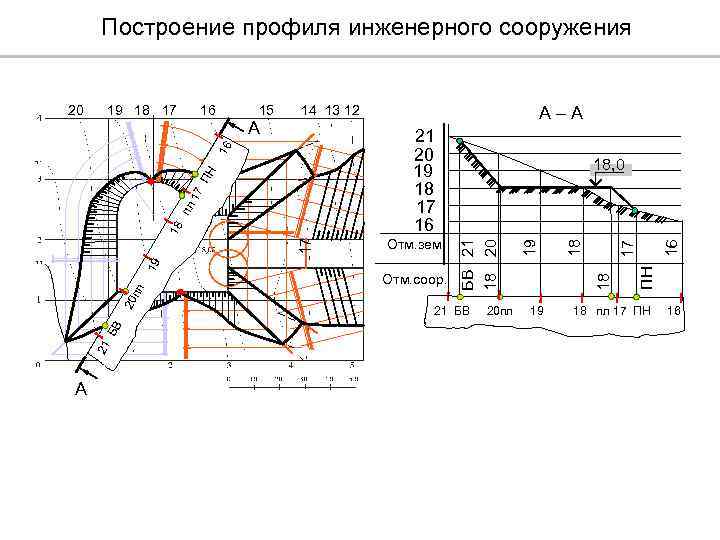
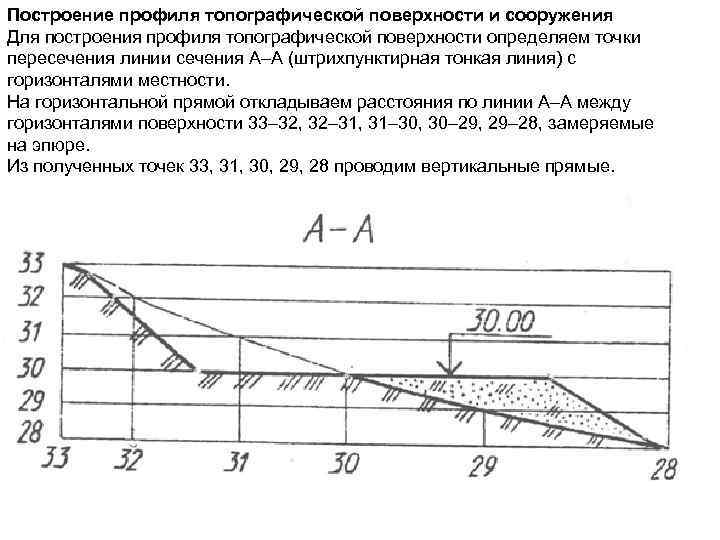Построение профиля топографической поверхности и сооружения Для построения профиля топографической поверхности определяем точки пересечения линии сечения A–A (штрихпунктирная тонкая линия) с горизонталями местности. На горизонтальной прямой откладываем расстояния по линии A–A между горизонталями поверхности 33– 32, 32– 31, 31– 30, 30– 29, 29– 28, замеряемые на эпюре. Из полученных точек 33, 31, 30, 29, 28 проводим вертикальные прямые.

Параллельно горизонтальной прямой проводим прямые 29, 30, 31, 32, 33 с интервалом, равным единице превышения горизонталей местности (одному метру). Через точки пересечения горизонтальных и вертикальных прямых с одинаковыми отметками, проводим кривую профиля топографической поверхности. Для построения профиля земляного сооружения замеряем по линии A–A расстояние от 30–й горизонтали местности до границ земляного сооружения. Данные расстояния откладываем на горизонтальной прямой вправо и влево от 30–й точки. Для построения линии откосов, необходимо замерить расстояние между горизонталями откосов по линии сечения. Эти расстояния откладываются на соответствующих горизонтальных прямых профиля от конечных точек площадки. Через полученные точки проводим линию сечения откосов.

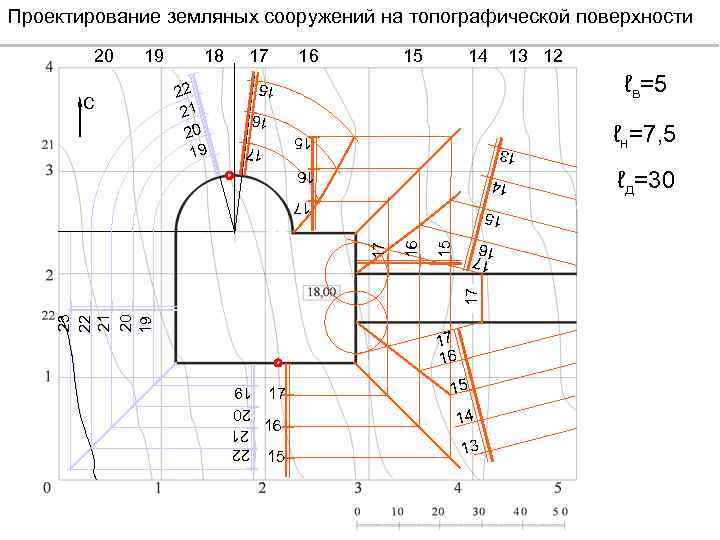Проектирование земляных сооружений на топографической поверхности 16 15 14 13 12 ℓв=5 13 17 22 21 20 19 17 15 С 18 16 19 15 20 16 14 17 15 23 22 21 20 19 17 16 17 15 17 16 15 15 14 13 ℓн=7, 5 ℓд=30 22 21 20 19

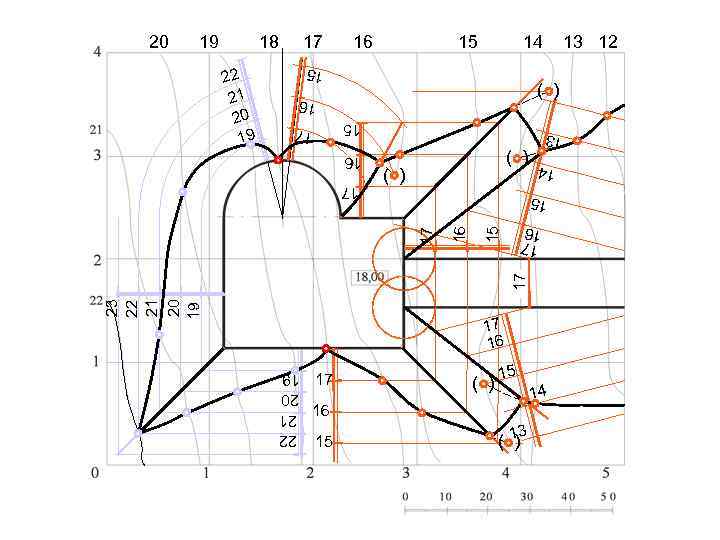16 15 14 13 12 ( ) 15 ( ) 14 17 22 21 20 19 17 13 18 16 19 15 20 16 17 15 23 22 21 20 19 17 16 17 15 17 16 17 ( ) 15 14 16 15 3 (1 ) 22 21 20 19

18 16 15 14 13 12 15 13 17 22 21 20 19 17 16 19 15 20 16 14 17 15 21 20 19 22 17 16 17 15 14 16 15 13

Построение профиля инженерного сооружения 21 20 19 18 17 16 Отм. соор. 21 БВ 20 пл 19 16 ПН 17 Отм. зем. 18, 0 17 ПН пл 17 18 19 пл 20 БВ 21 А А–А 18 А 14 13 12 18 15 19 16 БВ 21 18 20 19 18 17 16 20 18 пл 17 ПН 16

ПОСТРОЕНИЕ ТЕНЕЙ В ОРТОГОНАЛЬНЫХ ПРОЕКЦИЯХ

Форма предмета воспринимается точнее, когда предмет освещен и на его поверхности образуется светотень. Изображение светотени на проекционных чертежах состоит из двух графических операций: - «геометрия теней» ; - «изображение светотени» ( «отмывка» ) Характер светотени зависит от положения предмета относительно источника света и направления лучей к поверхности.

Светотень выявляет объемную форму пространственных объектов. Изображение светотени на чертеже, а также в аксонометрии и перспективе состоит из двух этапов: первый — это построение контуров (границ) теней точными приемами геометрических построений и второй — выявление и передача на чертеже градаций освещенности с учетом физических закономерностей и "воздушной" перспективы.

ВОЗДУШНАЯ ПЕРСПЕКТИВА Чем освещенное место ближе к зрителю, тем оно кажется светлее и ярче, а чем дальше – тем бледнее и мягче. Светотеневой контраст (различие между освещенной и теневой частью предмета) по мере удаления от зрителя погашается, делается менее резким.

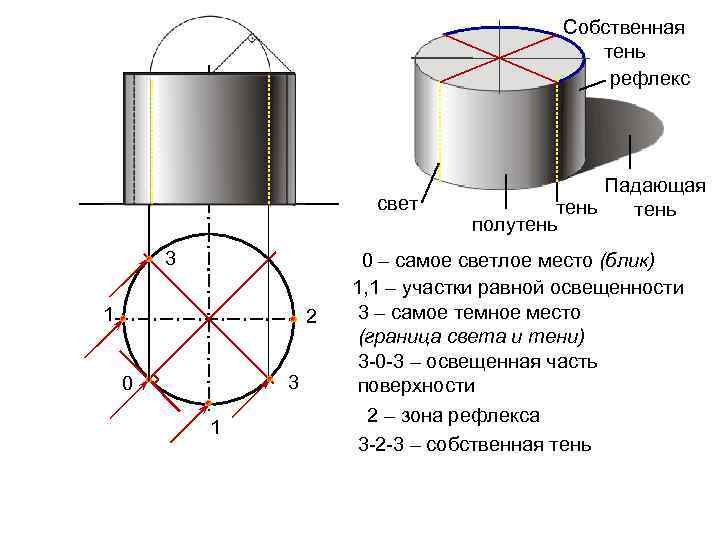Собственная тень рефлекс свет 3 1 2 3 0 1 Падающая тень полутень 0 – самое светлое место (блик) 1, 1 – участки равной освещенности 3 – самое темное место (граница света и тени) 3 -0 -3 – освещенная часть поверхности 2 – зона рефлекса 3 -2 -3 – собственная тень

Построение теней в ортогональных проекциях

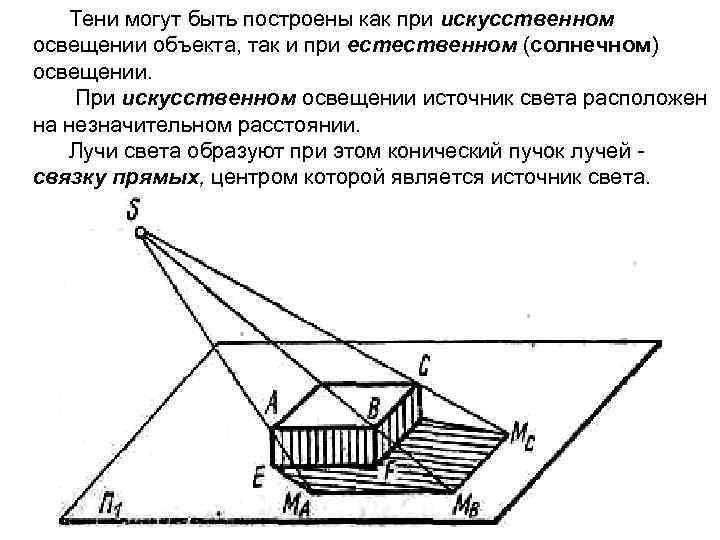Тени могут быть построены как при искусственном освещении объекта, так и при естественном (солнечном) освещении. При искусственном освещении источник света расположен на незначительном расстоянии. Лучи света образуют при этом конический пучок лучей связку прямых, центром которой является источник света.

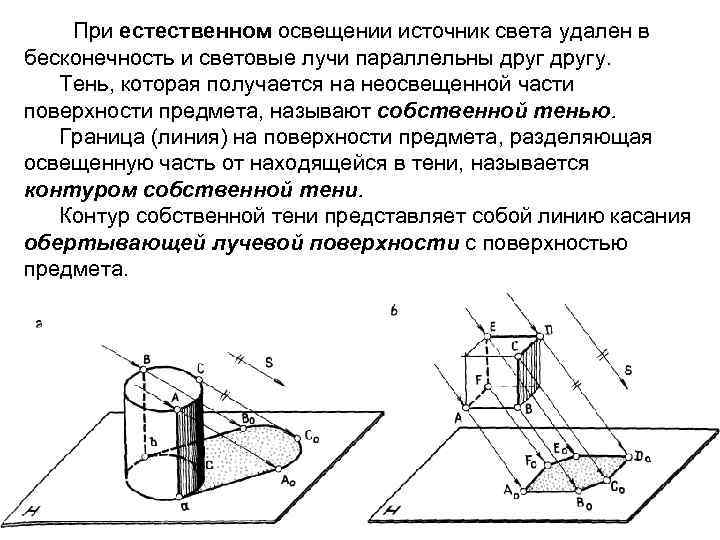При естественном освещении источник света удален в бесконечность и световые лучи параллельны другу. Тень, которая получается на неосвещенной части поверхности предмета, называют собственной тенью. Граница (линия) на поверхности предмета, разделяющая освещенную часть от находящейся в тени, называется контуром собственной тени. Контур собственной тени представляет собой линию касания обертывающей лучевой поверхности с поверхностью предмета. Рис. 2 а, б

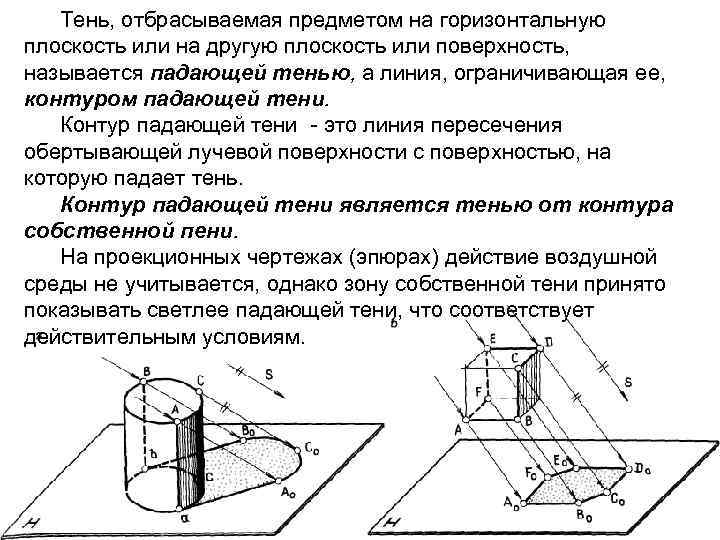Тень, отбрасываемая предметом на горизонтальную плоскость или на другую плоскость или поверхность, называется падающей тенью, а линия, ограничивающая ее, контуром падающей тени. Контур падающей тени - это линия пересечения обертывающей лучевой поверхности с поверхностью, на которую падает тень. Контур падающей тени является тенью от контура собственной пени. На проекционных чертежах (эпюрах) действие воздушной среды не учитывается, однако зону собственной тени принято показывать светлее падающей тени, что соответствует действительным условиям.

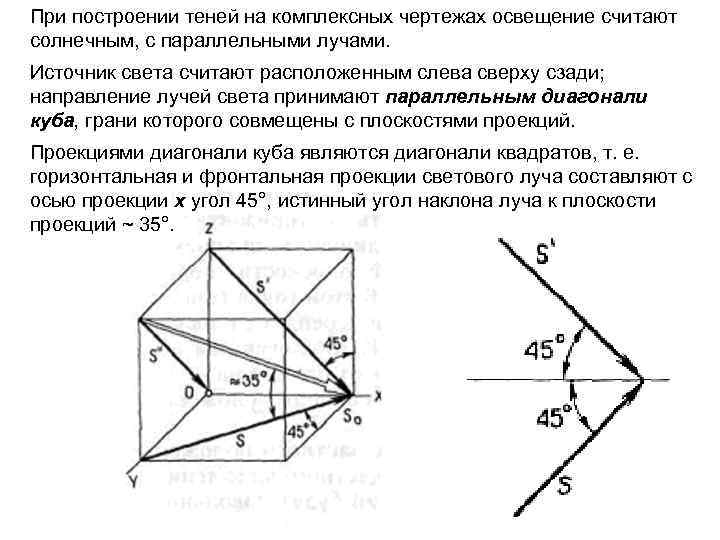При построении теней на комплексных чертежах освещение считают солнечным, с параллельными лучами. Источник света считают расположенным слева сверху сзади; направление лучей света принимают параллельным диагонали куба, грани которого совмещены с плоскостями проекций. Проекциями диагонали куба являются диагонали квадратов, т. е. горизонтальная и фронтальная проекции светового луча составляют с осью проекции х угол 45°, истинный угол наклона луча к плоскости проекций ~ 35°. Рис. 3

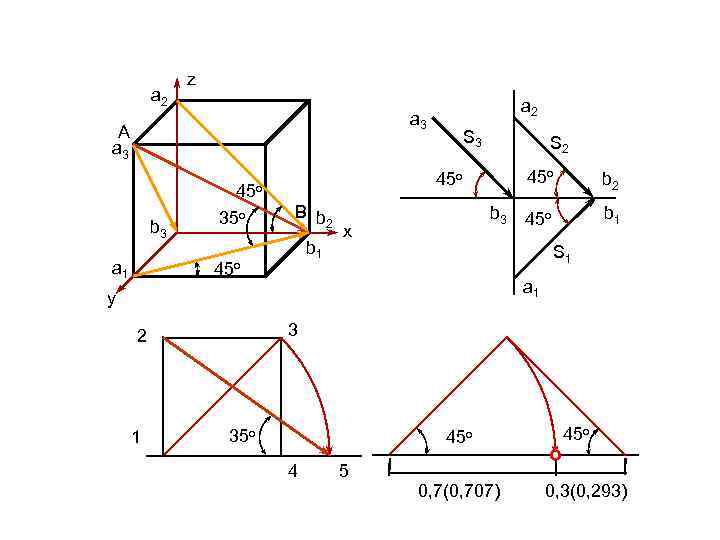a 2 z a 2 a 3 A a 3 b 3 a 1 S 2 45 о 45 о 35 о S 3 B b 2 b 1 45 о b 3 x 45 о b 1 S 1 a 1 y 3 2 1 b 2 35 о 4 45 о 5 0, 7(0, 707) 0, 3(0, 293)

Такое «стандартное» направление световых лучей создает определенные преимущества при построении теней и выполнении чертежа: 1) достигаются постоянство и простота построения проекции лучей и теней на чертежах фасада и плана объекта; 2) облегчаются чтение чертежа и понимание форм, пропорций и размеров элементов изображенного объекта, так как размер тени, отбрасываемой отдельными частями объекта, определяет в масштабе чертежа величину выступов и отступов от фронтальной плоскости предмета.

Построение падающей тени от точки. Позиционная задача на пересечение прямой с плоскостью. Тенью, падающей от точки на плоскость проекций, является соответствующий след луча света, проходящего через данную точку.

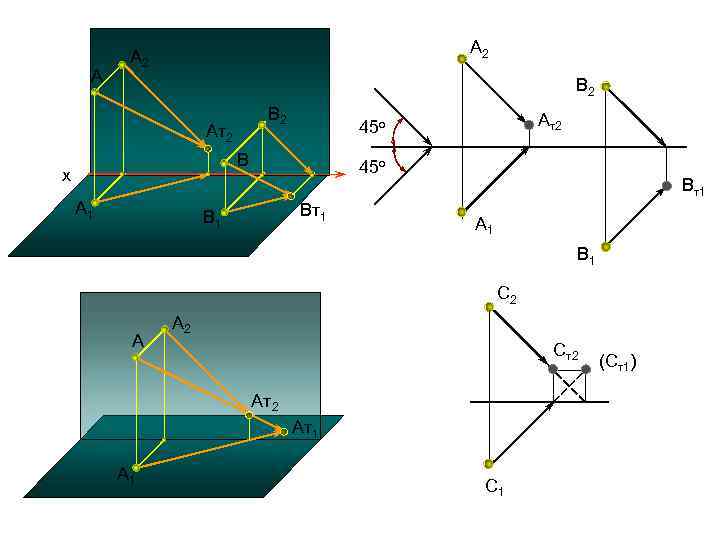A А 2 A 2 В 2 B 2 Aт2 B x A 1 Ат2 45 о Bт1 B 1 Вт1 А 1 В 1 С 2 A A 2 Ст2 Aт1 A 1 С 1 (Ст1)

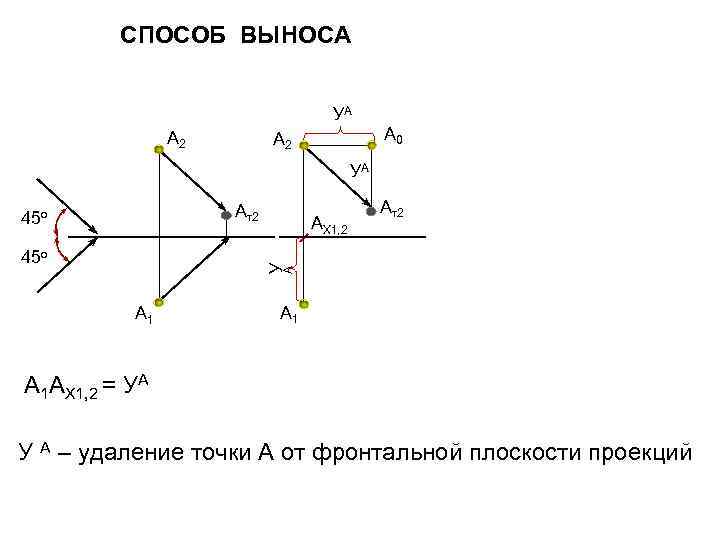СПОСОБ ВЫНОСА УА А 2 А 0 УА Ат2 45 о А У 45 о АХ 1, 2 Ат2 А 1 А 1 АХ 1, 2 = УА У А – удаление точки А от фронтальной плоскости проекций

Тени от прямых частного положения

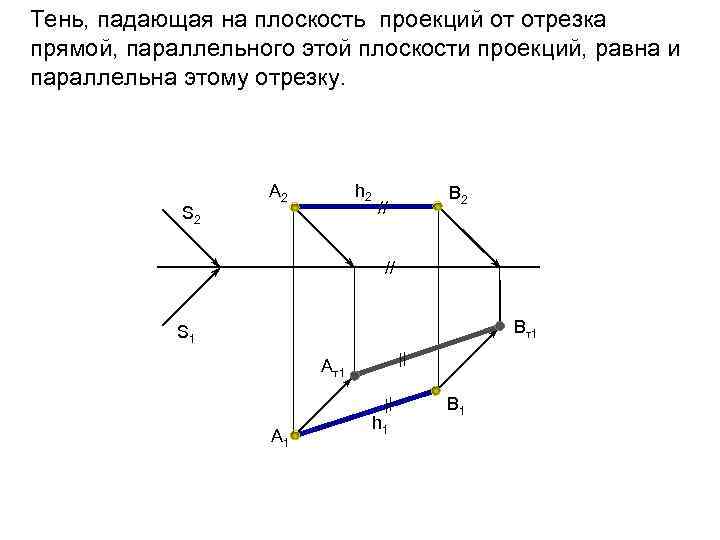Тень, падающая на плоскость проекций от отрезка прямой, параллельного этой плоскости проекций, равна и параллельна этому отрезку. S 2 h 2 А 2 В 2 // // Вт1 S 1 // Ат1 // А 1 h 1 В 1

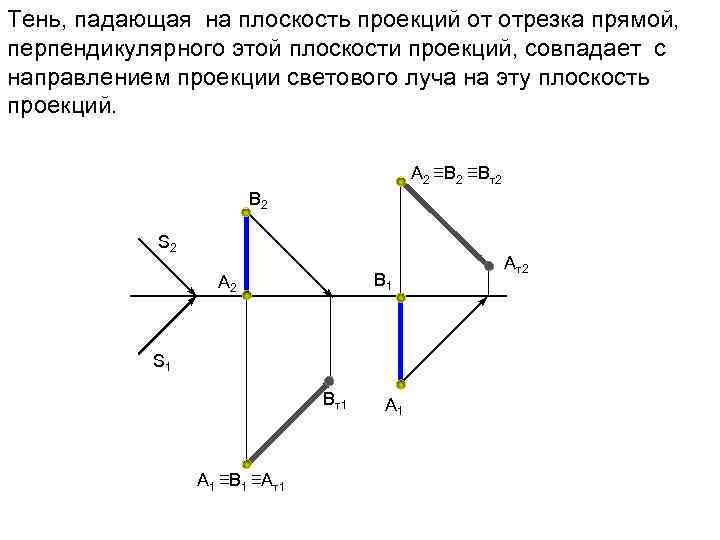Тень, падающая на плоскость проекций от отрезка прямой, перпендикулярного этой плоскости проекций, совпадает с направлением проекции светового луча на эту плоскость проекций. А 2 ≡Вт2 В 2 S 2 В 1 А 2 S 1 Вт1 А 1 ≡В 1 ≡Ат1 А 1 Ат2

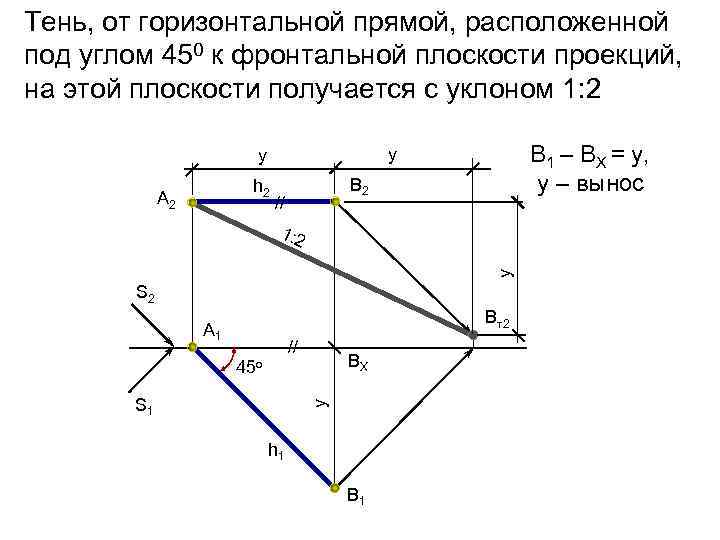Тень, от горизонтальной прямой, расположенной под углом 450 к фронтальной плоскости проекций, на этой плоскости получается с уклоном 1: 2 h 2 А 2 В 1 – ВХ = у, у – вынос y y В 2 // y 1: 2 S 2 Вт2 А 1 // 45 о y S 1 ВХ h 1 В 1

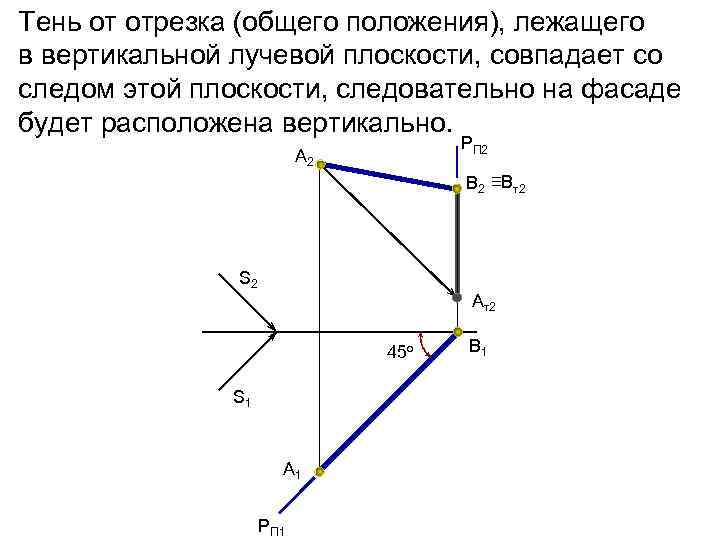Тень от отрезка (общего положения), лежащего в вертикальной лучевой плоскости, совпадает со следом этой плоскости, следовательно на фасаде будет расположена вертикально. РП 2 А 2 В 2 ≡Вт2 S 2 Ат2 45 о S 1 А 1 РП 1 В 1

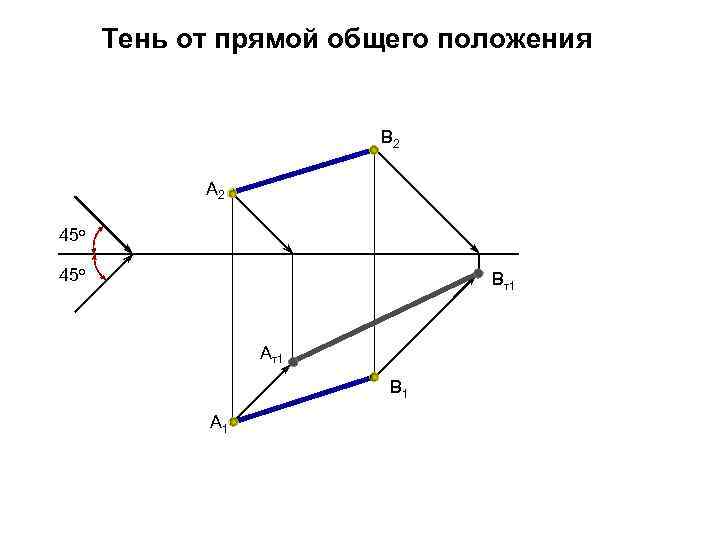Тень от прямой общего положения В 2 А 2 45 о Вт1 Ат1 В 1 А 1

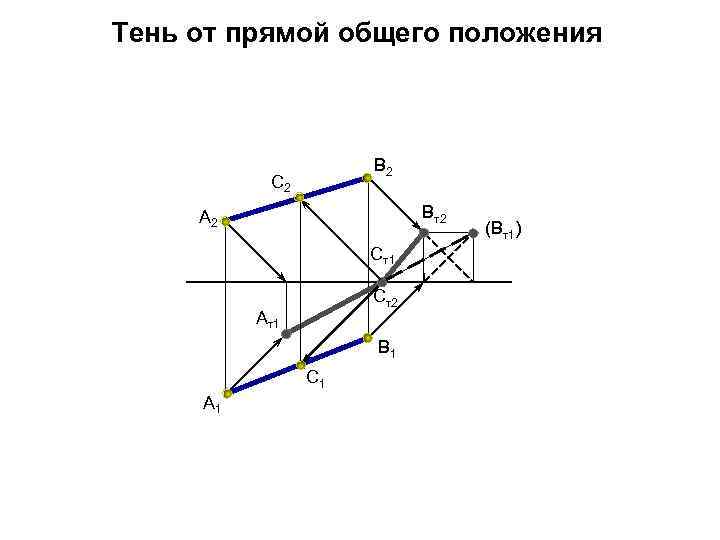Тень от прямой общего положения В 2 С 2 Вт2 А 2 Ст1 Ст2 Ат1 В 1 С 1 А 1 (Вт1)

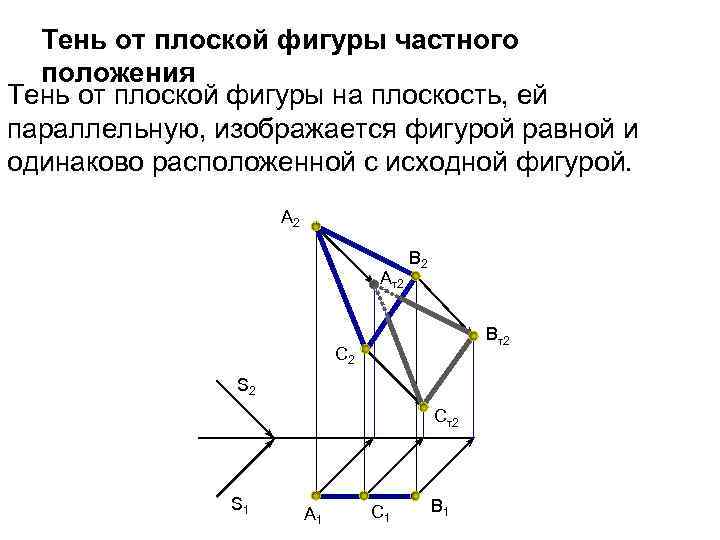Тень от плоской фигуры частного положения Тень от плоской фигуры на плоскость, ей параллельную, изображается фигурой равной и одинаково расположенной с исходной фигурой. А 2 Ат2 В 2 Вт2 С 2 S 2 Ст2 S 1 А 1 С 1 В 1