Поверхность свойства поверхности НТ-10 Рис 1 Пример

Поверхность, свойства поверхности НТ-10

Рис. 1. Пример простой поверхности Поверхность – граница раздела двух сред.

Свойства поверхности n 1. Поверхность определяется как множество точек, координаты которых удовлетворяют определённому виду уравнений:

Свойства поверхности n n Если функция непрерывна в некоторой точке и имеет в ней непрерывные частные производные, по крайней мере одна из которых не обращается в нуль, то в окрестности этой точки поверхность, заданная уравнением (1), будет правильной поверхностью. Помимо указанного выше неявного способа задания поверхность может быть определена явно, если одну из переменных, например z, можно выразить через остальные:

Свойства поверхности n Также существует параметрический способ задания. В этом случае поверхность определяется системой уравнений:

Свойства поверхности n n Интуитивно простую поверхность можно представить как кусок плоскости, подвергнутый непрерывным деформациям (растяжениям, сжатиям и изгибаниям). Примером простой поверхности является полусфера. Вся же сфера не является простой поверхностью

Рис. 2. Касательная плоскость в точке поверхности Касательная плоскость в точке гладкой поверхности — это плоскость, имеющая максимальный порядок соприкосновения с поверхностью в этой точке. Эквивалентный вариант определения: касательная плоскость есть плоскость, содержащая касательные ко всем гладким кривым, проходящим через эту точку.

Метрический тензор n n Свойства, сохраняющиеся при изометрических преобразованиях, называются внутренней геометрией поверхности. Внутренняя геометрия не зависит от положения поверхности в пространстве и не меняется при её изгибании без растяжения и сжатия (например, при изгибании цилиндра в конус).

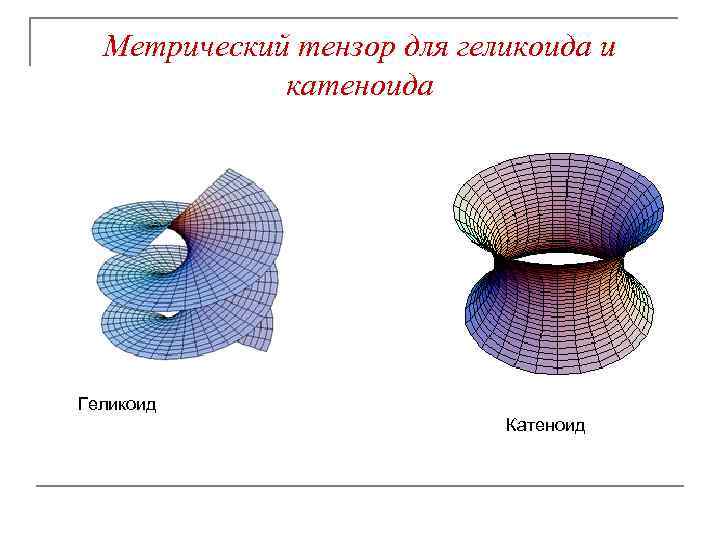Метрический тензор для геликоида и катеноида Геликоид Катеноид

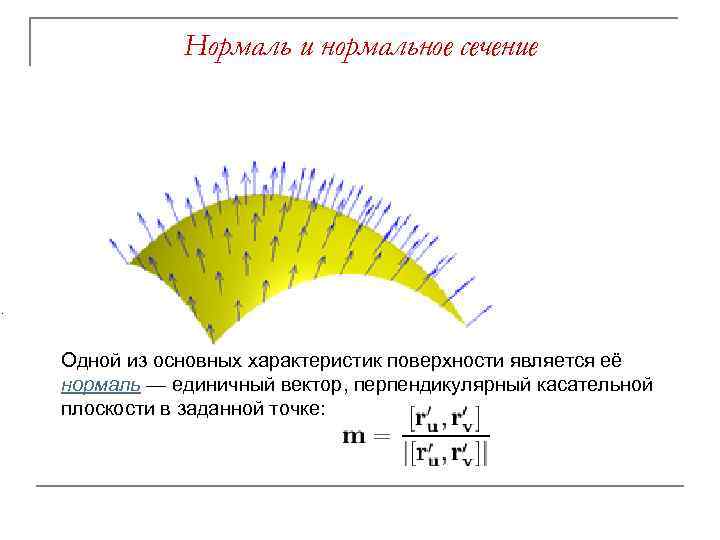Нормаль и нормальное сечение . Одной из основных характеристик поверхности является её нормаль — единичный вектор, перпендикулярный касательной плоскости в заданной точке:

Кривизна поверхности n n Для разных направлений в заданной точке поверхности получается разная кривизна нормального сечения, которая называется нормальной кривизной; ей приписывается знак плюс, если главная нормаль кривой идёт в том же направлении, что и нормаль к поверхности, или минус, если направления нормалей противоположны.

Поверхности с отрицательной (слева), нулевой (в центре) и положительной (справа) кривизной.

Свойства поверхности n n n Важной характеристикой поверхности является её ориентация. Поверхность называется двусторонней, если на всей её протяжённости она обладает непрерывным вектором нормали. В противном случае поверхность называют односторонней. Ориентированной называется двусторонняя поверхность с выбранным направлением нормали.

Свойства поверхности n Примерами односторонних, а следовательно и неориентируемых поверхностей являются бутылка Клейна или лента Мёбиуса. Лента Мёбиуса

Свойства поверхности n n n Бутылка Клейна — это определённая неориентируемая поверхность (то есть двумерное многообразие). Бутылка Клейна впервые была описана в 1882 г. немецким математиком Ф. Клейном. Она тесно связана с лентой Мёбиуса и проективной плоскостью. Название, по-видимому, происходит от неправильного перевода немецкого слова Fläche (поверхность), которое в немецком языке близко по написанию к слову Flasche (бутылка).

Свойства поверхности n Чтобы построить модель бутылки Клейна, необходимо взять бутылку с двумя отверстиями: в донышке и в стенке, вытянуть горлышко, изогнуть его вниз, и продев его через отверстие в стенке бутылки (для настоящей бутылки Клейна в четырёхмерном пространстве это отверстие не нужно, но без него нельзя обойтись в трёхмерном евклидовом пространстве), присоединить к отверстию на дне бутылки.

Бутылка Клейна, погружённая в трёхмерное простран n Если разрезать бутылку Клейна пополам вдоль её оси симметрии, то результатом будет лента Мёбиуса, изображенная справа (необходимо помнить, что изображенного пересечения на самом деле нет).

При рассечении бутылки Клейна получается лента Мёбиуса

Свойства поверхности n n ПОВЕРХНОСТЬ РАЗДЕЛА ФАЗ - граничная поверхность между различными фазами вещества. В понятие поверхности, или границы раздела фаз, прежде всего вкладывается геометрический смысл, т. е. нечто нематериальное, что разграничивает две соприкасающиеся материальные фазы. В математическом смысле это — двухмерный объект, не имеющий третьего измерения, т. е. толщины, массы и т. п. При таком понимании поверхность характеризуется величиной площади и кривизной (если отбросить несущественные в данном случае характеристики ее положения в пространстве).

Свойства поверхности n n К размерным характеристикам наноматериалов можно отнести следующие характеристики: - величину удельной поверхности (для нанопорошков), определяющую средний размер агрегатов; - средний размер частиц или зерен, средний размер ОКР; - распределение по размерам (гранулометрический состав) частиц, зерен, ОКР.

Свойства поверхности n n Величина удельной поверхности – одна из важнейших характеристик наноматериала, определяющая активность протекания физикохимических процессов, многие технологические свойства, взаимодействие с окружающей средой и т. д. Удельной поверхностью называют площадь, которую имеет 1 грамм (или килограмм) того или иного вещества. Обозначают эту величину как Sуд , ее размерность м 2/г, м 2/кг.

Свойства поверхности n n n Уменьшение диаметра частиц при прочих равных условиях увеличивает Sуд. Сфероидизация уменьшает удельную поверхность, поскольку шар имеет минимальную поверхность при данной дисперсности материала. Соответственно, изменение формы частиц при сохранении их размеров приводит к увеличению Sуд.

Свойства поверхности n n Шероховатость поверхности — совокупность неровностей поверхности с относительно малыми шагами выделенная, например, с помощью базовой линии или части плоскости. Измеряется в микрометрах (мкм). Шероховатость относится к микрогеометрии твёрдого тела и определяет его важнейшие эксплуатационные качества. Прежде всего, износостойкость от истирания, прочность, плотность (герметичность) соединений, химическая стойкость, внешний вид. В зависимости от условий работы поверхности назначается параметр шероховатости проектировании деталей машин, также существует связь между предельным отклонением размера и шероховатостью.

Поверхностные явления проявляются в гетерогенных системах, т. е. системах, между компонентами которых имеется поверхность раздела. Поверхностными явлениями называют процессы, происходящие на границе раздела фаз и их причиной служит особое энергетическое состояние частиц (атомов, молекул, ионов) поверхностного слоя.

Все поверхности раздела в зависимости от агрегатного состояния граничащих фаз делят на 2 типа: 1. Подвижные поверхности раздела: между жидкостью и газом (Ж-Г) и двумя несмешивающимися жидкостями (Ж-Ж). 2. Неподвижные поверхности раздела: между твердым телом и газом (Т-Г), твердым телом и жидкостью (Т-Ж).

Формирование наноразмерных структур на поверхности раздела фаз n n Предложен новый метод синтеза полупроводниковых наностержней гидроксида кадмия из Cd(C 6 H 5 N 2 O 2)2 посредством реакции на поверхности раздела толуола и водного раствора гидроксида натрия Полученные наноструктуры можно использовать в качестве прекурсора для формирования наностержней Cd. O и Cd. S.

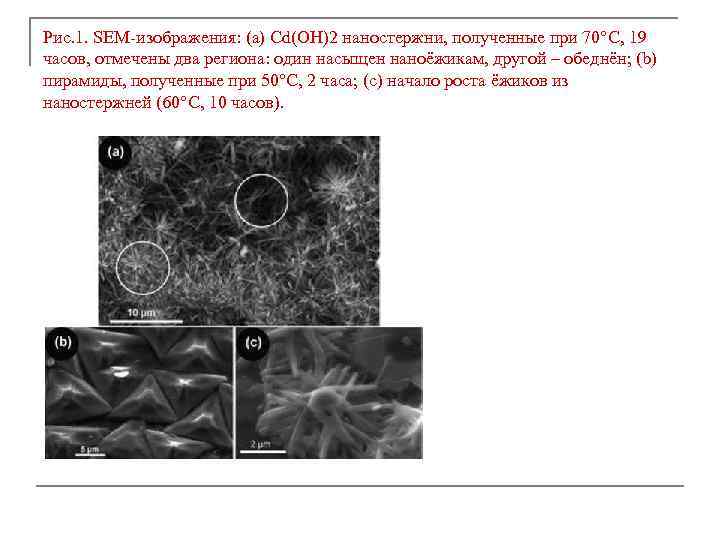Рис. 1. SEM-изображения: (a) Cd(OH)2 наностержни, полученные при 70°С, 19 часов, отмечены два региона: один насыщен наноёжикам, другой – обеднён; (b) пирамиды, полученные при 50°С, 2 часа; (c) начало роста ёжиков из наностержней (60°С, 10 часов).

Формирование наноразмерных структур на поверхности раздела фаз n n Диаметр стержней меньше 200 нм, а длина их составляет единицы микрон. Учёные также предложили механизм образования "ёжиков" из наностержней гидроксида кадмия (рис. 2). Важную роль в этом процессе играет смешиваемость водного слоя с толуолом. Смешивание существует практически всегда в той или иной степени. Образовавшиеся на поверхности раздела слоёв изначально сферические "капли" стремятся снизить свою поверхностную энергию и образуют на границе эмульсию Пикеринга.

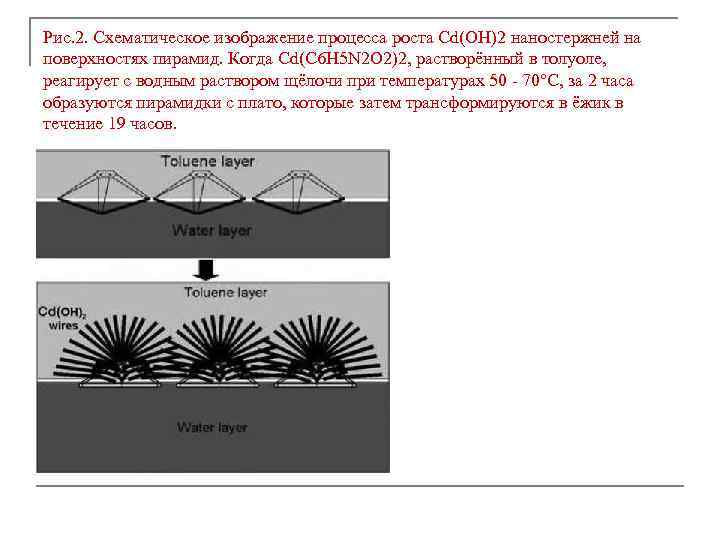Рис. 2. Схематическое изображение процесса роста Cd(OH)2 наностержней на поверхностях пирамид. Когда Cd(C 6 H 5 N 2 O 2)2, растворённый в толуоле, реагирует с водным раствором щёлочи при температурах 50 - 70°С, за 2 часа образуются пирамидки с плато, которые затем трансформируются в ёжик в течение 19 часов.

Формирование наноразмерных структур на поверхности раздела фаз Рис. 3. Рентгенограммы (a) наностержней, Рис. 4. TEM-изображения Cd(OH)2 полученных при температуре 70°С, 19 часов и (b) наностержней и HRTEM-изображение пирамидок, полученных при температуре 50°С, 2 (вставка). часа. Оба образца состоят из фазы Cd(OH)2 со структурой брукита

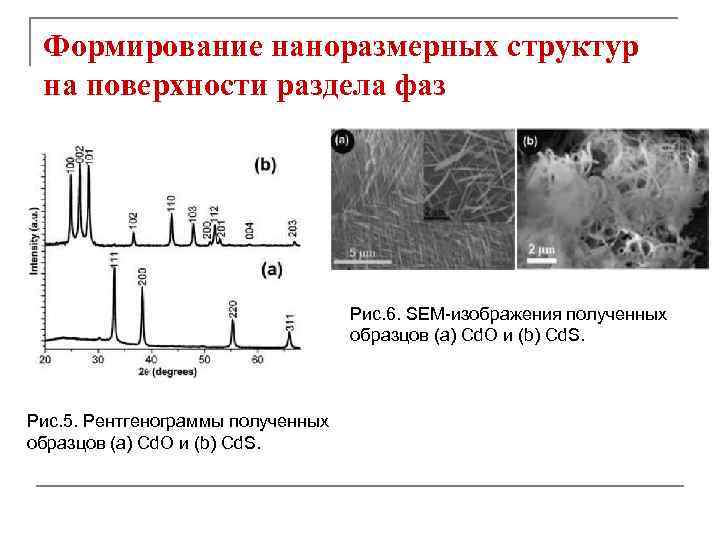Формирование наноразмерных структур на поверхности раздела фаз Рис. 6. SEM-изображения полученных образцов (a) Cd. O и (b) Cd. S. Рис. 5. Рентгенограммы полученных образцов (a) Cd. O и (b) Cd. S.

Рекомендуемая литература n ОСНОВНАЯ ЛИТЕРАТУРА n Ролдугин В. И. Физикохимия поверхности. - Долгопрудный: Изд. Дом «Интеллект» , 2008. – 568 с. 2. Адамсон А. Физическая химия поверхностей. - М: Мир, 1979. – 567 с. 3. Джейкок М. , Парфит Д. Химия поверхностей раздела фаз. - М. : Мир. 1984. Суздалев И. П. Физико-химия нанокластеров, наноструктур и наноматериалов. - М. : Ком. Книга, 2006. – 592 с. Сумм Б. Д. Основы коллоидной химии. 2 -е издание. М. : Академия, 2007. -239 с. Зимон А. Д. , Лещенко Н. Ф. Коллоидная химия. М. : АГАР, 2003. 318 с. Фенелонов В. Б. , Введение в физическую химию формирования супрамолекулярной структуры адсорбентов и катализаторов. - изд. СО РАН, Новосибирск, 2002. Боресков Г. К. , Гетерогенный катализ. - Новосибирск, Наука, 1986. Щукин Е. Д. , Перцов А. В. , Амелина Е. А. , Коллоидная химия. - М. Высшая школа, 1992. n n n

Рекомендуемая литература n n n ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА 1. Грин М. Поверхностные свойства твердых тел. М. : Мир. 1996. 2. Вудраф Д. , Делчар Т. Современные методы исследования поверхности. М. : Мир, 1989. 3. Ребиндер П. А. Поверхностные явления в дисперсных системах. – М. : Наука, 1979. – 381 4. Фролов Ю. Г. Курс коллоидной химии. Поверхностные явления и дисперсные системы. М. Химия. 1989. – 462 с. 5. Лен Ж. -М. Супрамолекулярная химия. - Новосибирск, Наука, 1998 г; 6. Карнаухов А. П. , Адсорбция. Текстура дисперсных и пористых материалов. - Наука, Новосибирск, 1999. 7. Грег Г. , Синг К. , Адсорбция, удельная поверхность, пористость. - М. , Мир, 1984. 8. Э. Зенгуил "Физика поверхности". М. , Мир, 1990. 536 стр. 9. Ф. Бехштедт, Р. Эндерлайн "Поверхности и границы раздела полупроводников". М. , Мир, 1990.