11-Потоки в сетя,л.11.ppt
- Количество слайдов: 25
 Потоки в сетях.
Потоки в сетях.
 Варианты задач:
Варианты задач:
 Задачи о MAX потоке Рассмотрим граф G=(X, A) с пропускными способностями дуг g, i, j, источником S и стоком t. S, t X. Множество чисел , определенных на дугах ( , называется потоками в дугах, если выполняется условие максимальной.
Задачи о MAX потоке Рассмотрим граф G=(X, A) с пропускными способностями дуг g, i, j, источником S и стоком t. S, t X. Множество чисел , определенных на дугах ( , называется потоками в дугах, если выполняется условие максимальной.
 ), Теорема Форда-Фалкерсона: (о максимальном потоке и максимальном разрезе). Доказательство.
), Теорема Форда-Фалкерсона: (о максимальном потоке и максимальном разрезе). Доказательство.


 Алгоритм начинает работу с произвольного допустимого потока (можно взять и 0 -й поток), затем стремится увеличить величину потока с помощью систематического поиска всех возможных аугментальных целей потока от s к t. Поиск аугментальной цели осуществляется с помощью расставленных пометок в вершинах графа. Поэтому указывают, вдоль каких дуг может быть увеличен поток и на сколько. Как только найдена одна из таких цепей, поток вдоль нее увеличивают до max значения, а пометки в вершинах стираются и вновь полученный поток используется в качестве исходного при новой расстановке пометок. Алгоритм работу заканчивает и дает max поток, если нельзя найти ни 1 аугментальную цель.
Алгоритм начинает работу с произвольного допустимого потока (можно взять и 0 -й поток), затем стремится увеличить величину потока с помощью систематического поиска всех возможных аугментальных целей потока от s к t. Поиск аугментальной цели осуществляется с помощью расставленных пометок в вершинах графа. Поэтому указывают, вдоль каких дуг может быть увеличен поток и на сколько. Как только найдена одна из таких цепей, поток вдоль нее увеличивают до max значения, а пометки в вершинах стираются и вновь полученный поток используется в качестве исходного при новой расстановке пометок. Алгоритм работу заканчивает и дает max поток, если нельзя найти ни 1 аугментальную цель.
 Алгоритм расстановки пометок для задачи о max (от s и t) потоке. А. Расстановка пометок.
Алгоритм расстановки пометок для задачи о max (от s и t) потоке. А. Расстановка пометок.

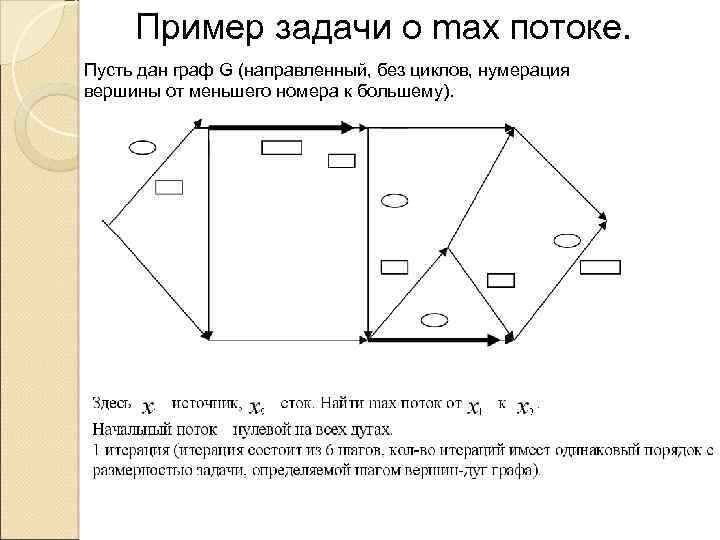 Пример задачи о max потоке. Пусть дан граф G (направленный, без циклов, нумерация вершины от меньшего номера к большему).
Пример задачи о max потоке. Пусть дан граф G (направленный, без циклов, нумерация вершины от меньшего номера к большему).


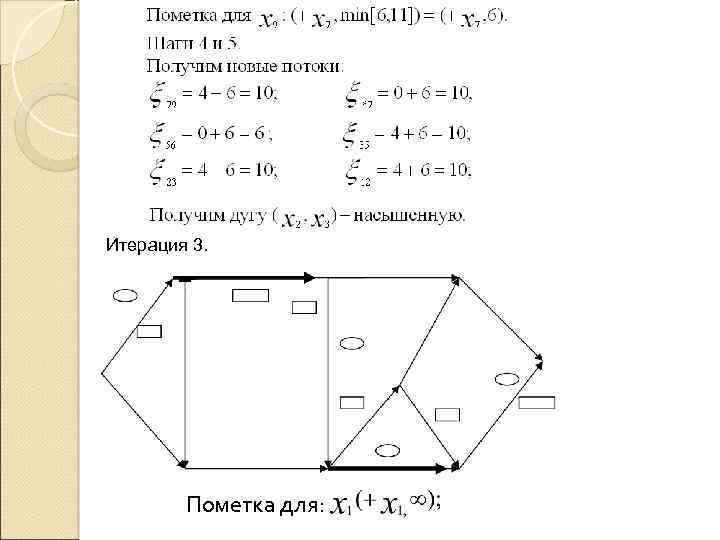 Итерация 3. Пометка для:
Итерация 3. Пометка для:
 Пометка для
Пометка для
 Пометка для не получена и не может быть получена. Новые потоки;
Пометка для не получена и не может быть получена. Новые потоки;
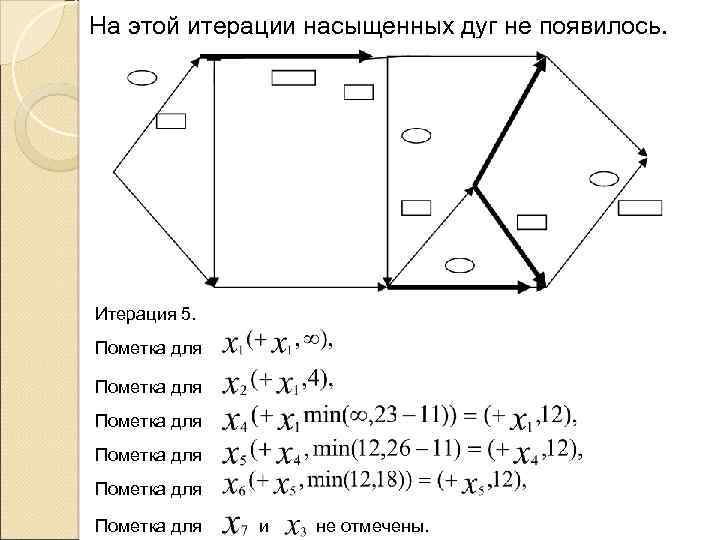 На этой итерации насыщенных дуг не появилось. Итерация 5. Пометка для Пометка для и не отмечены.
На этой итерации насыщенных дуг не появилось. Итерация 5. Пометка для Пометка для и не отмечены.
 Пометка для Новые потоки; Появилась насыщенная дуга Итерация 6. Пометка для не может быть помечена.
Пометка для Новые потоки; Появилась насыщенная дуга Итерация 6. Пометка для не может быть помечена.
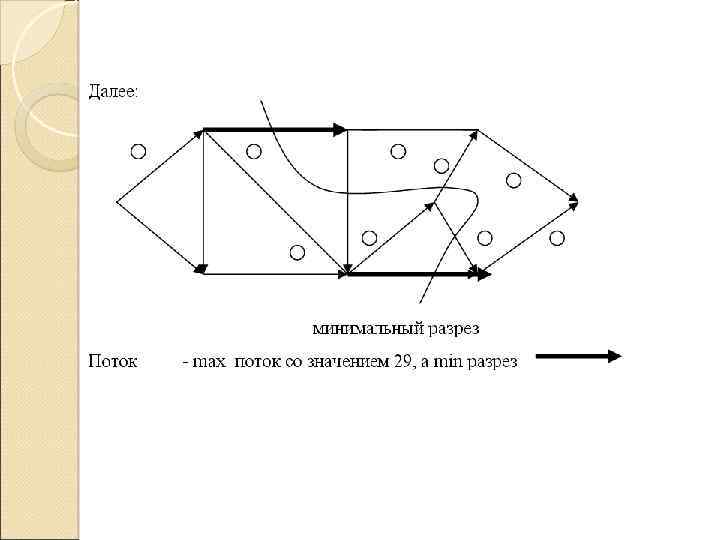
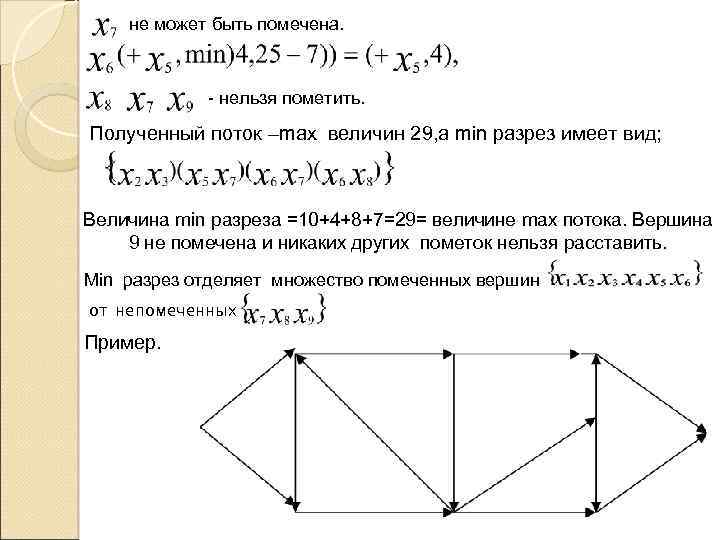 не может быть помечена. - нельзя пометить. Полученный поток –max величин 29, а min разрез имеет вид; Величина min разреза =10+4+8+7=29= величине max потока. Вершина 9 не помечена и никаких других пометок нельзя расставить. Min разрез отделяет множество помеченных вершин от непомеченных Пример.
не может быть помечена. - нельзя пометить. Полученный поток –max величин 29, а min разрез имеет вид; Величина min разреза =10+4+8+7=29= величине max потока. Вершина 9 не помечена и никаких других пометок нельзя расставить. Min разрез отделяет множество помеченных вершин от непомеченных Пример.
 - источник; - сток; Пропускные способности дуг указаны на рисунке. Найти max поток от к Начальный поток – с нулевыми значениями на всех дугах. Шаг 1. Припишем пометку Шаг 2. (1) множество вершин есть не помечена. 2. Множество вершин Итак, помечена и просмотрена, а все остальные вершины и не помечены и не просмотрены,
- источник; - сток; Пропускные способности дуг указаны на рисунке. Найти max поток от к Начальный поток – с нулевыми значениями на всех дугах. Шаг 1. Припишем пометку Шаг 2. (1) множество вершин есть не помечена. 2. Множество вершин Итак, помечена и просмотрена, а все остальные вершины и не помечены и не просмотрены,
 Повторим шаг 2 и первой просмотрим вершину Теперь вершины и помечены и просмотрены, а и помечены, но не просмотрены. Взяв для просмотра и повторяя шаг 2, прейдем к следующим пометкам; пометкой будет Беря для просмотра Продолжим просмотр с для пометкой будет найдем, что никаких пометок расставить нельзя получим следующие потоки:
Повторим шаг 2 и первой просмотрим вершину Теперь вершины и помечены и просмотрены, а и помечены, но не просмотрены. Взяв для просмотра и повторяя шаг 2, прейдем к следующим пометкам; пометкой будет Беря для просмотра Продолжим просмотр с для пометкой будет найдем, что никаких пометок расставить нельзя получим следующие потоки:
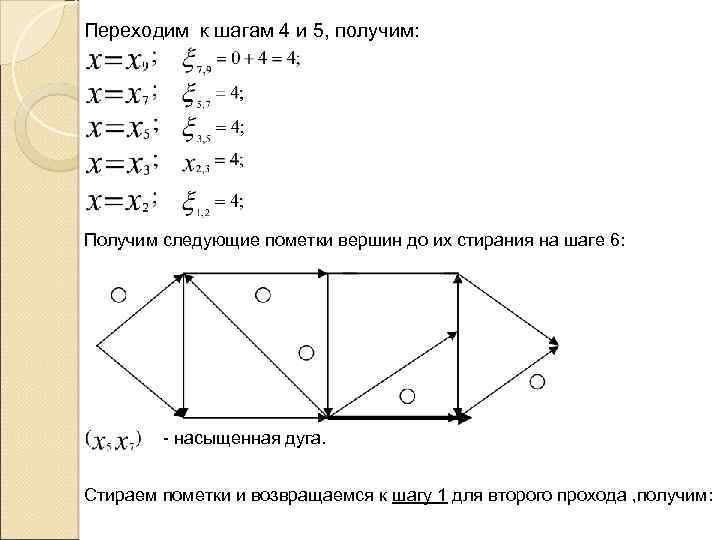 Переходим к шагам 4 и 5, получим: Получим следующие пометки вершин до их стирания на шаге 6: - насыщенная дуга. Стираем пометки и возвращаемся к шагу 1 для второго прохода , получим:
Переходим к шагам 4 и 5, получим: Получим следующие пометки вершин до их стирания на шаге 6: - насыщенная дуга. Стираем пометки и возвращаемся к шагу 1 для второго прохода , получим:
 помечена и просмотрена. решена и просмотрена. также помечена и просмотрена.
помечена и просмотрена. решена и просмотрена. также помечена и просмотрена.
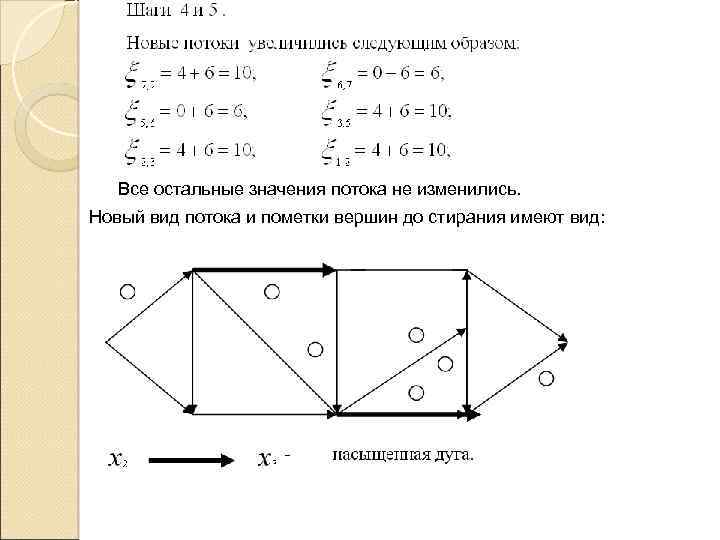 Все остальные значения потока не изменились. Новый вид потока и пометки вершин до стирания имеют вид:
Все остальные значения потока не изменились. Новый вид потока и пометки вершин до стирания имеют вид: