Потоки в сетях Сеть это ориентированный нагруженный

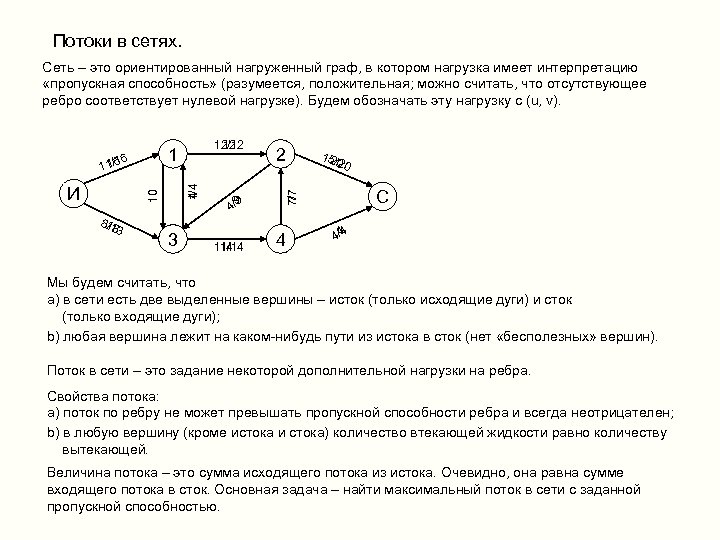Потоки в сетях. Сеть – это ориентированный нагруженный граф, в котором нагрузка имеет интерпретацию «пропускная способность» (разумеется, положительная; можно считать, что отсутствующее ребро соответствует нулевой нагрузке). Будем обозначать эту нагрузку c (u, v). 811 / 33 3 9 4/9 11/14 14 2 15/ 20 20 С 7 7/7 1/4 4 10 И 12/12 12 1 1 16 11/6 4 / 444 Мы будем считать, что a) в сети есть две выделенные вершины – исток (только исходящие дуги) и сток (только входящие дуги); b) любая вершина лежит на каком-нибудь пути из истока в сток (нет «бесполезных» вершин). Поток в сети – это задание некоторой дополнительной нагрузки на ребра. Свойства потока: a) поток по ребру не может превышать пропускной способности ребра и всегда неотрицателен; b) в любую вершину (кроме истока и стока) количество втекающей жидкости равно количеству вытекающей. Величина потока – это сумма исходящего потока из истока. Очевидно, она равна сумме входящего потока в сток. Основная задача – найти максимальный поток в сети с заданной пропускной способностью.

Потоки в сетях. Пусть задана сеть и поток в ней. Свяжем с потоком функцию f (u, v), обладающую следующими свойствами: 8/1 3 3 9 4/ 11/14 2 15/ 20 С 7/7 1/4 10 И 12/12 1 6 11/1 4 4/4 a) если по ребру (u, v) идет поток величиной c, то положим f (u, v) = c, f (v, u) = -c; b) если есть два «встречных» потока c 1 и c 2 по ребрам (u, v) и (v, u) соответственно, то полагаем f (u, v) = c 1 -c 2. На самом деле всегда можно считать, что на самом деле есть только один поток величиной |c 1 -c 2|. На приведенной выше картинке: f (И, 3) = 8; f (3, 2) = -4; f (1, 3) = -1. Для каждого ребра (при заданном потоке f) определим также его «остаточную пропускную способность» : cf(u, v) = c (u, v) – f(u, v) Например, для заданного потока cf(3, 4) = 3, cf(1, 3) = 11.

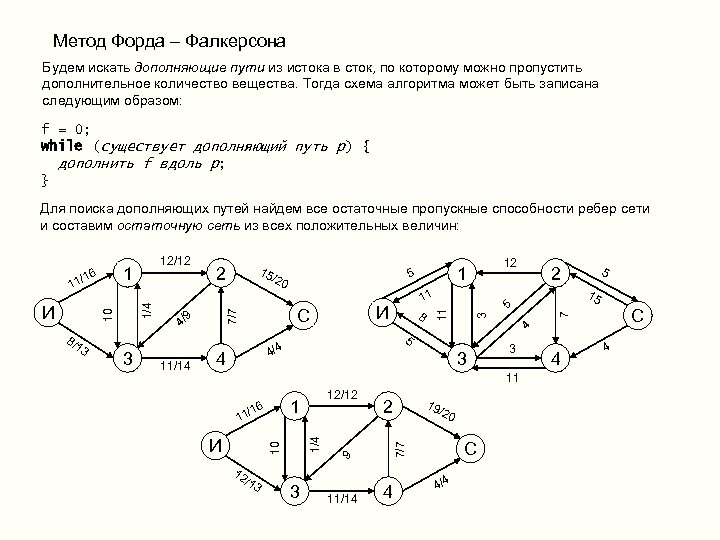Метод Форда – Фалкерсона Будем искать дополняющие пути из истока в сток, по которому можно пропустить дополнительное количество вещества. Тогда схема алгоритма может быть записана следующим образом: f = 0; while (существует дополняющий путь p) { дополнить f вдоль p; } Для поиска дополняющих путей найдем все остаточные пропускные способности ребер сети и составим остаточную сеть из всех положительных величин: 5 4/4 4 3 12 /13 3 9 11/14 2 19 /20 С 7/7 1 11 И 12/12 4 4/4 15 С 4 3 11 /16 5 7 И С 2 5 3 11 8 11 9 4/ 11/14 /20 12 1 5 1/4 3 15 10 8/1 3 2 7/7 10 1/4 11 И 12/12 1 /16 4 4

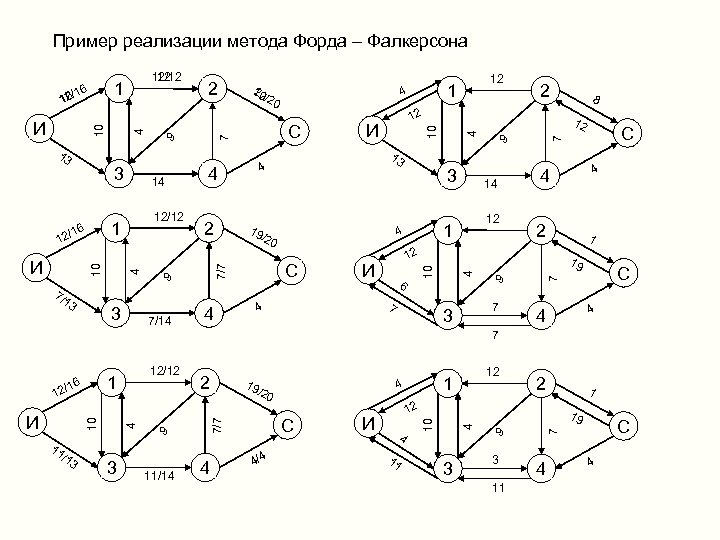Пример реализации метода Форда – Фалкерсона 3 3 4 С 7 2 12 И 6 7 4 12 1 19 9 7 3 С 4 4 14 1 4 /20 4 10 7 9 7/14 19 3 9 С 7 4 10 7/1 2 13 8 12 4 1 И 12/12 2 12 И 4 12 1 4 С 4 14 1 6 2/1 9 12 20 /20 10 3 2 7/7 13 4 10 И 12/12 12 1 6 6/1 12 4 4 7 /13 3 11/14 4 2 12 И 4 11 3 1 19 9 3 11 С 7 С 4/4 1 4 /20 12 4 19 10 4 10 11 9 2 7/7 12 И 12/12 1 /16 4 4

Выбор дополняющего пути в методе Форда – Фалкерсона Если выбор дополняющего пути производится не очень удачно, то процедура поиска максимального потока может затянуться. 1 00 0 00 И 0 С 0 00 2 1 1/1 0 0 000 И 1/1 0 00 0 2 999 1 И 1 00 0 1 2 1 00 0 00 1 0 С 999 00 0 00 С 1 1/1 0 00 00 0 10 1/1 00 999 1 1 1/1 1 0 000 0 00 / 111 00 /1 0 и так далее, всего 2 000 шагов… 000 1 Можно попробовать искать кратчайший (по числу ребер) дополняющий путь между истоком и стоком. Например, с помощью поиска в ширину. Получающийся при этом алгоритм (реализация метода Форда – Фалкерсона) называется алгоритмом Эдмондса – Карпа). Можно показать, что в алгоритме Эдмондса – Карпа число шагов ограничено сверху числом 2 nm, где m – число ребер в сети, а n – число вершин. Поскольку поиск в ширину, изменение потоков вдоль ребер и построение остаточной сети требуют времени O(m), то общее время работы алгоритма можно оценить как O(m 2 n).

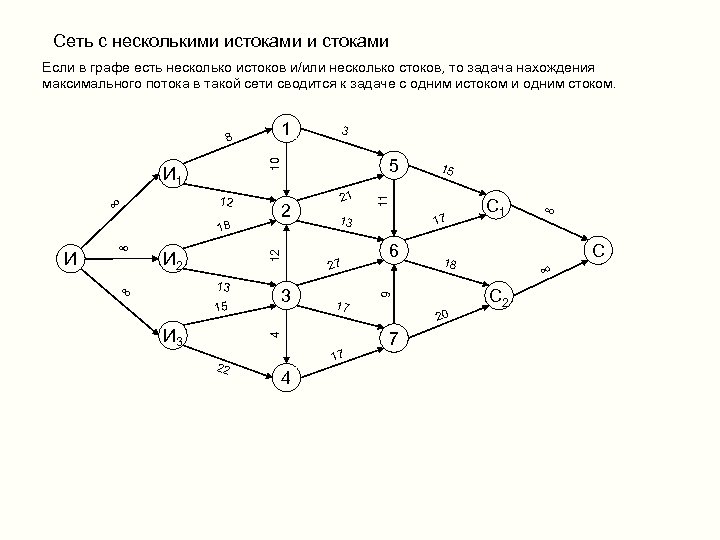Сеть с несколькими истоками и стоками Если в графе есть несколько истоков и/или несколько стоков, то задача нахождения максимального потока в такой сети сводится к задаче с одним истоком и одним стоком. 2 12 И 2 ∞ 13 15 И 3 27 3 22 17 17 4 17 13 4 ∞ 21 15 11 12 18 И 5 10 И 1 ∞ 3 6 20 7 С 1 ∞ С 18 9 1 8 ∞ С 2

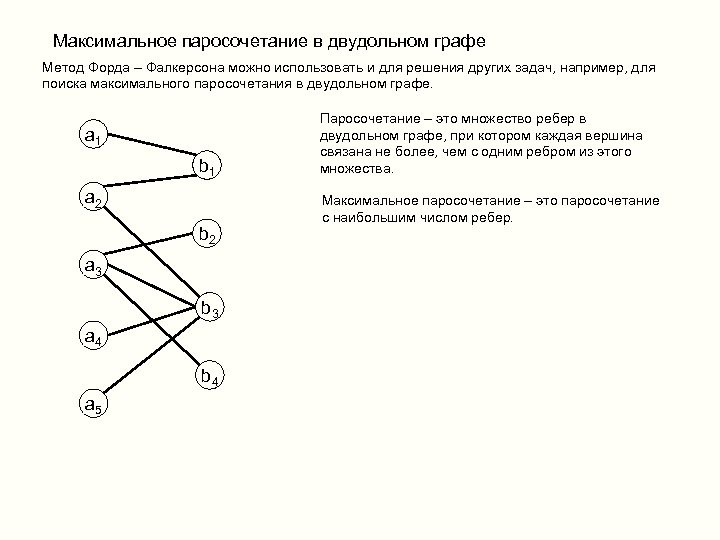Максимальное паросочетание в двудольном графе Метод Форда – Фалкерсона можно использовать и для решения других задач, например, для поиска максимального паросочетания в двудольном графе. a 1 b 1 a 2 b 2 a 3 b 3 a 4 b 4 a 5 Паросочетание – это множество ребер в двудольном графе, при котором каждая вершина связана не более, чем с одним ребром из этого множества. Максимальное паросочетание – это паросочетание с наибольшим числом ребер.

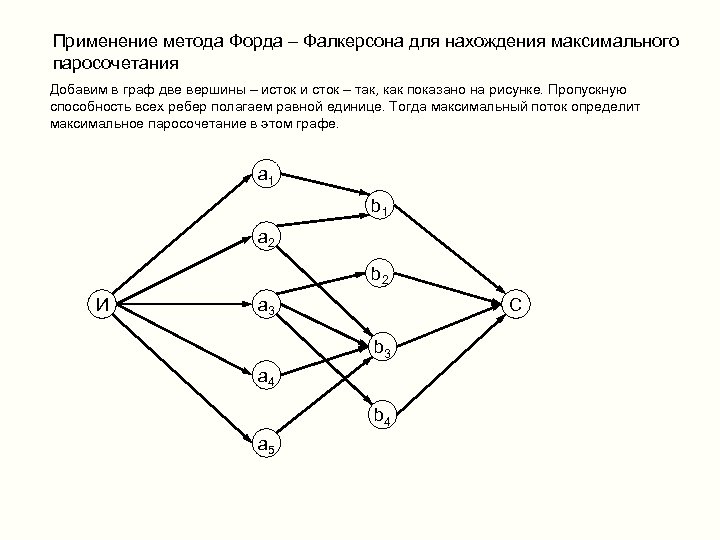Применение метода Форда – Фалкерсона для нахождения максимального паросочетания Добавим в граф две вершины – исток и сток – так, как показано на рисунке. Пропускную способность всех ребер полагаем равной единице. Тогда максимальный поток определит максимальное паросочетание в этом графе. a 1 b 1 a 2 b 2 И a 3 С b 3 a 4 b 4 a 5

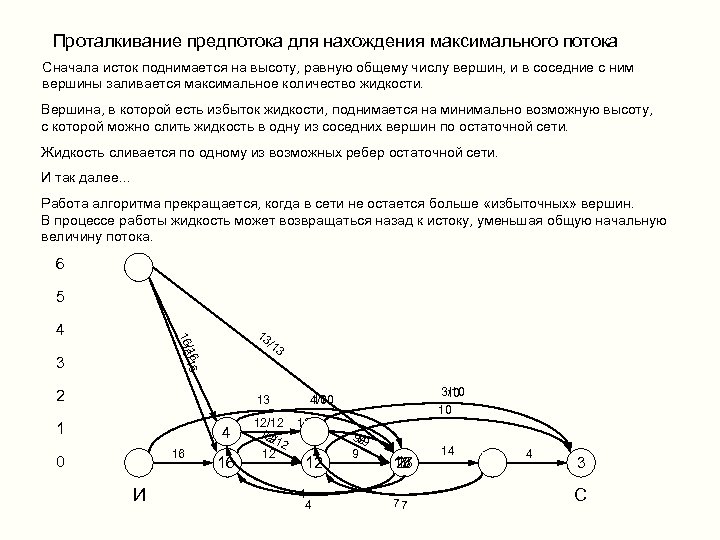Проталкивание предпотока для нахождения максимального потока Сначала исток поднимается на высоту, равную общему числу вершин, и в соседние с ним вершины заливается максимальное количество жидкости. Вершина, в которой есть избыток жидкости, поднимается на минимально возможную высоту, с которой можно слить жидкость в одну из соседних вершин по остаточной сети. Жидкость сливается по одному из возможных ребер остаточной сети. И так далее. . . Работа алгоритма прекращается, когда в сети не остается больше «избыточных» вершин. В процессе работы жидкость может возвращаться назад к истоку, уменьшая общую начальную величину потока. 6 5 13 /1 /1616 / 1616 4 3 3 2 13 1 4 16 0 И 16 3/10 10 10 4/10 10 12/12 10 12 12 /12 12 12 4 4 999 / 9 13 26 17 77 14 4 3 С

Реализация алгоритма проталкивания предпотока for (int i = 0; i < n; ++i) { h[i] = 0; e[i] = 0; } h[s] = n; for (Arc arc : arcs) { int u = arc. start; v = arc. end; f[u, v] = f[v, u] = 0; } for (int u : adj(s)) { f[s, u] = c[s, u]; f[u, s] = -c[s, u]; e[u] = c[s, u]; } while (есть избыточные вершины) { for (int u : excs) { if (возможно проталкивание избытка) протолкнуть избыток; else поднять вершину; } } Никакая вершина не может быть поднята на высоту, большую или равную 2 n. Поэтому общее число операций подъема не может быть больше 2 n 2. Можно показать, что общее число операций оценивается как O(n 2 m), что лучше, чем в алгоритме Эдмондса – Карпа (O(nm 2)).