Постройте график функции Х 1 f x

Постройте график функции Х – 1, § f(x)= если -5 ≤ x ≤ 0, (x – 1)2 – 2, если 0 < x ≤ 3, 2, если 3 < x ≤ 5.

Свойства функции y=f(x). § 1. D(f) = [-5; 5]; § 2. убывает на отрезке [0; 1], возрастает на отрезках [-5; 0] и [1; 3]; § 3. ограниченная; § 4. унаим = -6; унаиб = 2; § 5. непрерывная; § 6. Е(f) = [-6; 2]; § 7. выпукла вниз на отрезке [0; 3].

Исследуйте § на монотонность функцию У = х3 + 3 х ; на ограниченность функцию У = √(25 – х2 ).

Тема урока «Свойства функций» . § Цели урока: § - изучить свойства монотонности и ограниченности функций; § - научить исследовать функцию на монотонность, ограниченность снизу, сверху;

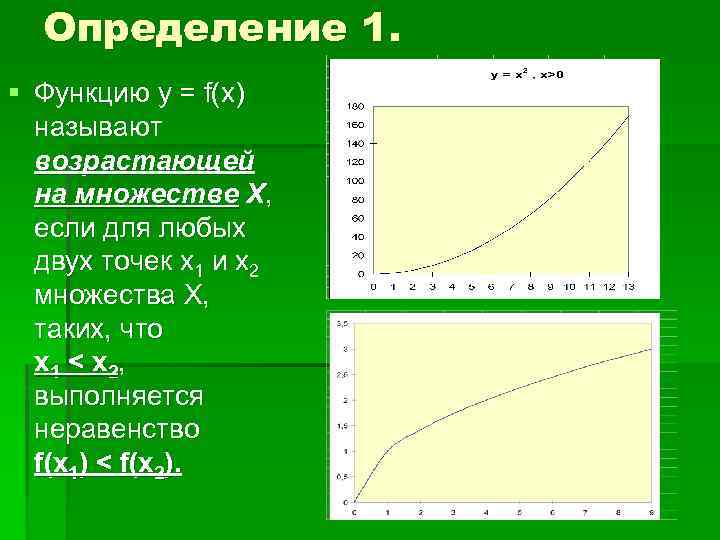Определение 1. § Функцию у = f(x) называют возрастающей на множестве Х, если для любых двух точек х1 и х2 множества Х, таких, что х 1 < х 2, выполняется неравенство f(x 1) < f(x 2).

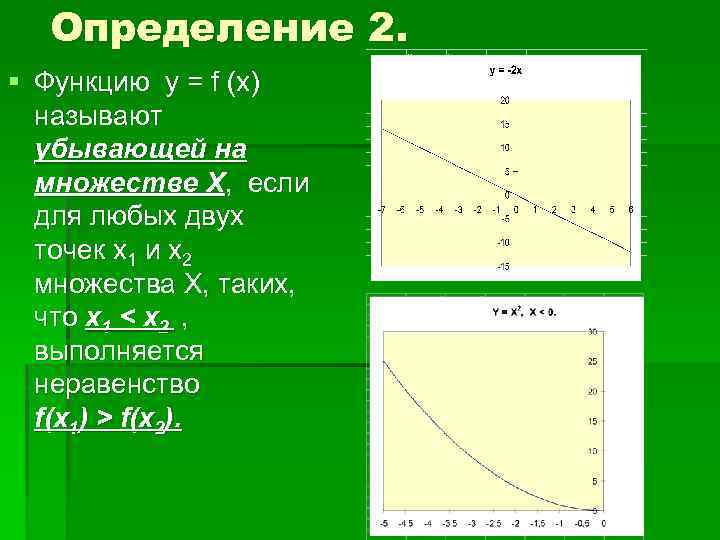Определение 2. § Функцию у = f (x) называют убывающей на множестве Х, если для любых двух точек х1 и х2 множества Х, таких, что х1 < х2 , выполняется неравенство f(x 1) > f(x 2).

Определите характер монотонности функции у = х3 + 3 х. § Пусть х1 < х2, тогда Х 13 < х 23, 3 х1 < 3 х2, Х 13 +3 х1 < х23 +3 х2. 3 Т. е. f(x 1) < f(x 2). Следовательно функция у = x +3 x возрастает на всей числовой прямой.

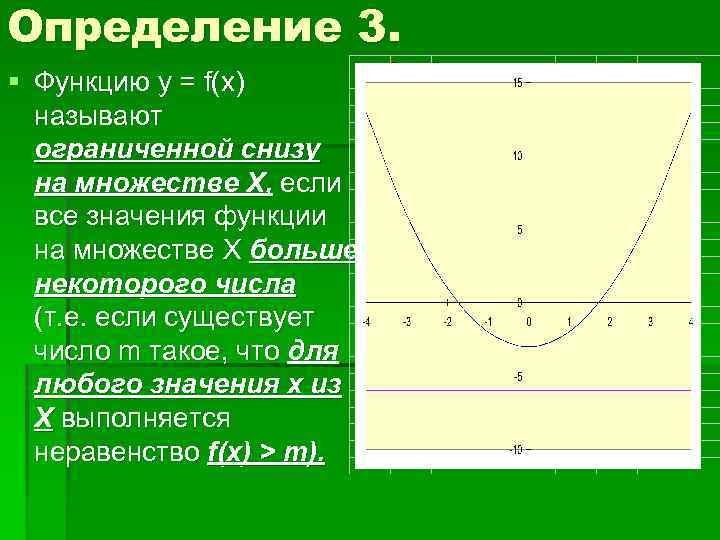Определение 3. § Функцию у = f(x) называют ограниченной снизу на множестве Х, если все значения функции на множестве Х больше некоторого числа (т. е. если существует число m такое, что для любого значения х из Х выполняется неравенство f(x) > m).

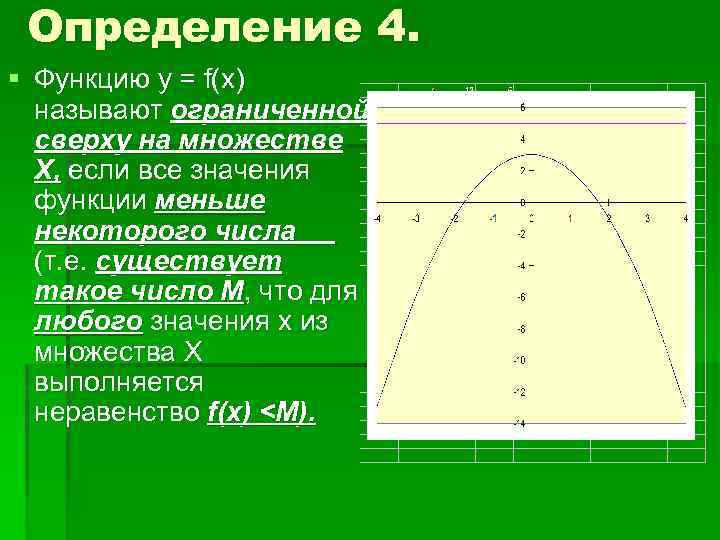Определение 4. § Функцию у = f(x) называют ограниченной сверху на множестве Х, если все значения функции меньше некоторого числа (т. е. существует такое число М, что для любого значения х из множества Х выполняется неравенство f(x) <М).

Исследуйте функцию у = √(25 – х2) на ограниченность. 1. √(25 – х2) ≥ 0, т. е. ф - ия ограничена снизу. 2. х2 ≥ 0, -х 2 ≤ 0, 25 – х2 ≤ 25, √(25 – х2) ≤ 5, т. е. ф – ия ограничена сверху. Следовательно 0 ≤ √(25 – х2) ≤ 5, т. е. функция ограниченная.

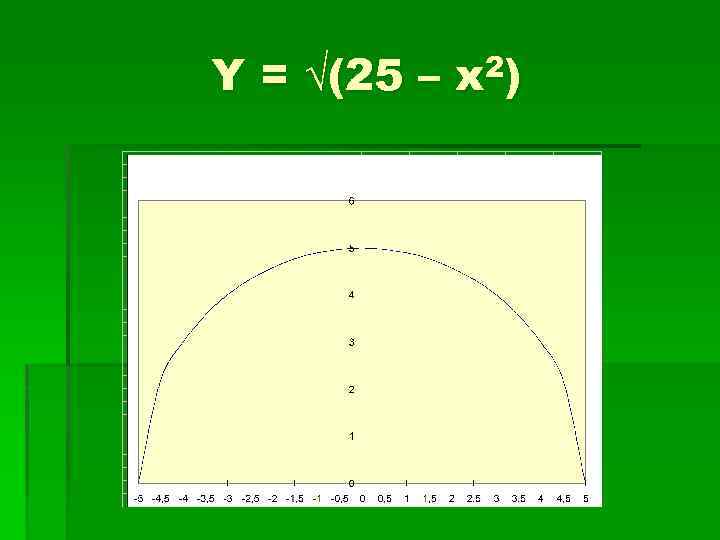Y = √(25 – x 2)

Домашнее задание § § 9 (стр. 76 -78); § № 253(г) и 257(г), 259(а) и 261(а); Изобразить график функции: Е(f)=[-3; 10], D(f)=[-4; 6], возрастает на промежутке [-4; 0], убывает на промежутке [0; 6].