Построение сечений многогранников Урок геометрии в 10 классе

Построение сечений многогранников Урок геометрии в 10 классе Учитель математики СОШ № 115 г Перми Арапова Т. А.

Основные методы построения сечений Метод, основанный на использовании аксиом и теорем стереометрии Метод внутреннего проектирования Метод следов Х Учитель математики Арапова Т. А.

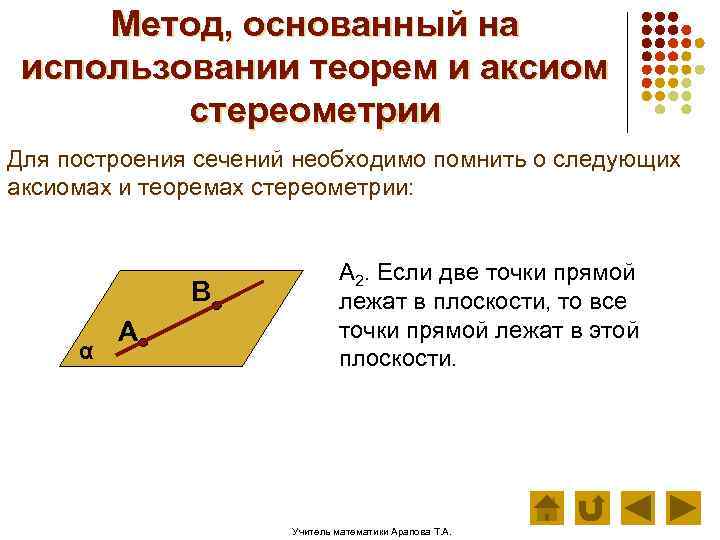Метод, основанный на использовании теорем и аксиом стереометрии Для построения сечений необходимо помнить о следующих аксиомах и теоремах стереометрии: В α А А 2. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости. Учитель математики Арапова Т. А.

Метод, основанный на использовании теорем и аксиом стереометрии Для построения сечений необходимо помнить о следующих аксиомах и теоремах стереометрии: а А А 3. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей. α β Учитель математики Арапова Т. А.

Метод, основанный на использовании теорем и аксиом стереометрии Для построения сечений необходимо помнить о следующих аксиомах и теоремах стереометрии: Т 3. Если две параллельные плоскости пересечены третьей, линии их пересечения параллельны. α β γ Учитель математики Арапова Т. А.

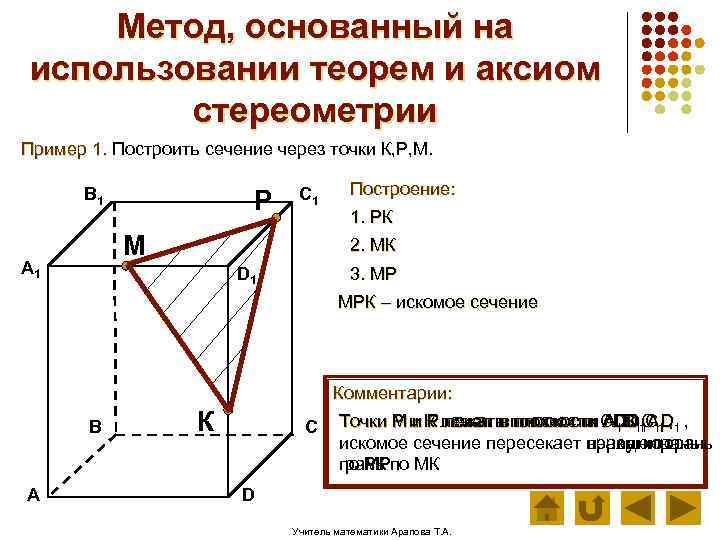Метод, основанный на использовании теорем и аксиом стереометрии Пример 1. Построить сечение через точки К, Р, М. В 1 Р C 1 М А 1 Построение: 1. РК 2. МК D 1 3. МР МРК – искомое сечение Комментарии: В А К С Точки Р и К лежат в плоскости CDD 1 C 1 , М и К лежат в плоскости АDD 1 А 1 Р лежат в плоскости А 1 В 1 С 1 D искомое сечение пересекает правую грань верхнюю грань переднюю грань по РК по МК МР D Учитель математики Арапова Т. А.

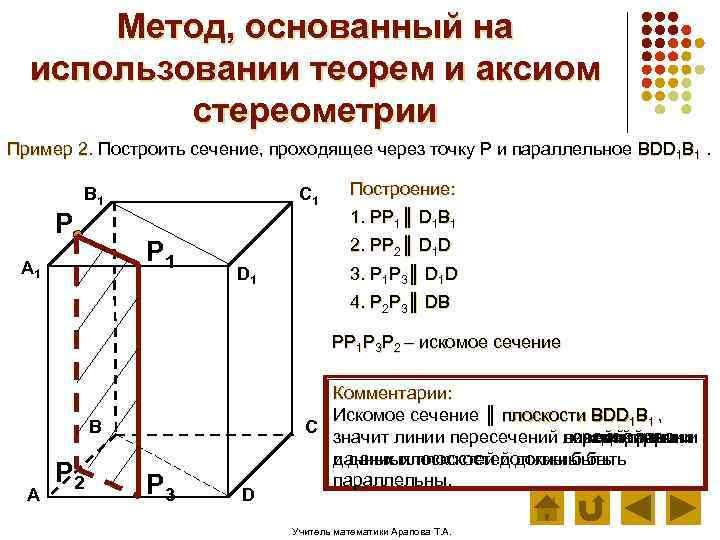Метод, основанный на использовании теорем и аксиом стереометрии Пример 2. Построить сечение, проходящее через точку Р и параллельное ВDD 1 В 1. В 1 Р C 1 Р 1 А 1 Построение: 1. РР 1║ D 1 В 1 2. РР 2║ D 1 D D 1 3. Р 1 Р 3║ D 1 D 4. Р 2 Р 3║ DВ РР 1 Р 3 Р 2 – искомое сечение В А Р 2 Р 3 D Комментарии: Искомое сечение ║ плоскости ВDD 1 В 1 , С значит линии пересечений верхнейграни ии нижней грани передней грани левой грани и и данных плоскостей должны быть параллельны. Учитель математики Арапова Т. А.

Метод, основанный на использовании теорем и аксиом стереометрии Пример 3. Построить сечение, проходящее через точки МРК. Построение: В C 1 1 А 1 D 1 М Р О 1 А В К О 3 О 4 С О 2 D 1. МР 2. РК 3. МР∩АD=О 1 4. О 1 К∩СВ=О 2 5. РК∩ВВ 1=О 3 6. О 2 О 3∩СС 1=О 4 7. МО 4 РКО 2 О 4 М – искомое сечение Комментарии: Прямые ии. Р 1 лежат в в плоскости В 1 ВА Точки М 2 РКОлежатввплоскости А 11 D 1 DА О О лежат плоскости А CD К и. Р и 4 ВВ 1 лежат на левой грани лежат плоскости АВ С 1 В 1 ВС искомое сечение искомое, сечение пересекает переднюю нижнюю левую пересекает 2 грань по МРзаднюю грань по О 2 О 4 КО КР Учитель математики Арапова Т. А.

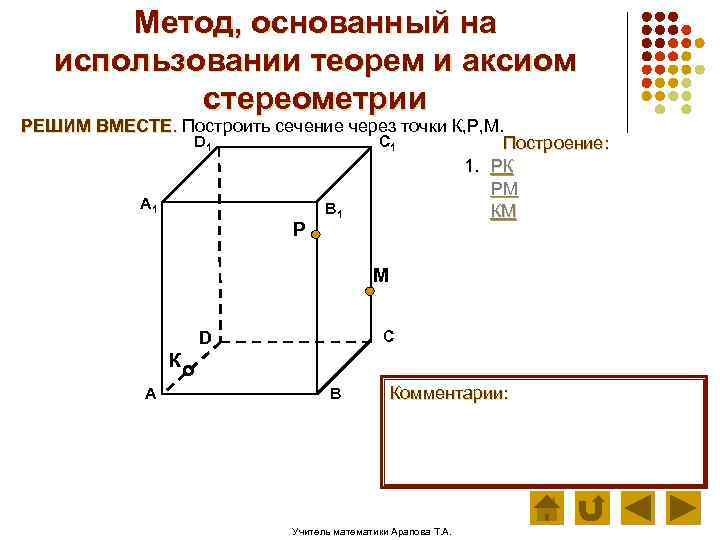Метод, основанный на использовании теорем и аксиом стереометрии РЕШИМ ВМЕСТЕ. Построить сечение через точки К, Р, М. D 1 C 1 Построение: 1. РК РМ А 1 В 1 КМ Р М С D К А В Комментарии: Учитель математики Арапова Т. А.

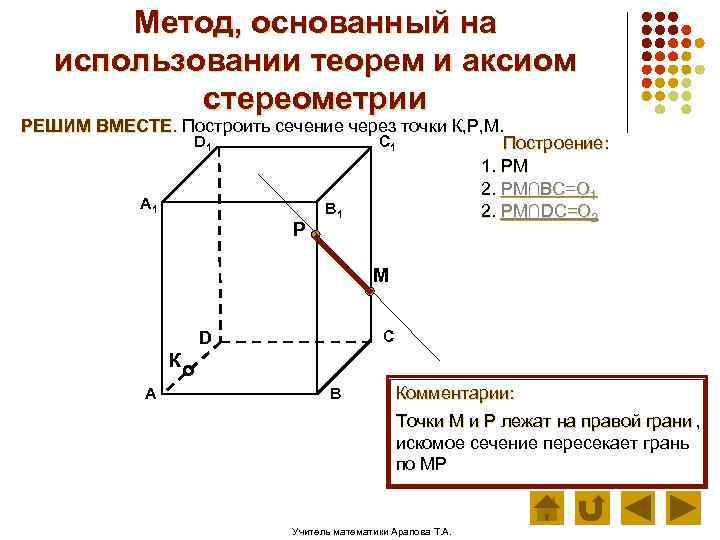Метод, основанный на использовании теорем и аксиом стереометрии РЕШИМ ВМЕСТЕ. Построить сечение через точки К, Р, М. D 1 C 1 Построение: 1. РМ 2. РМ∩ВС=О 1 А 1 В 1 2. РМ∩DС=О 2 Р М С D К А В Комментарии: Точки М и Р лежат на правой грани , искомое сечение пересекает грань по МР Учитель математики Арапова Т. А.

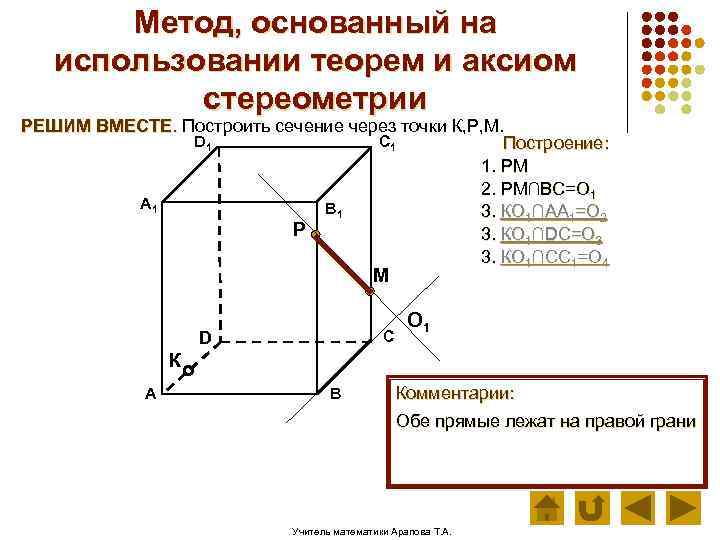Метод, основанный на использовании теорем и аксиом стереометрии РЕШИМ ВМЕСТЕ. Построить сечение через точки К, Р, М. D 1 C 1 Построение: 1. РМ 2. РМ∩ВС=О 1 А 1 В 1 3. КО 1∩АА 1=О 2 Р 3. КО 1∩DC=О 3 3. КО 1∩CC 1=О 4 М С D О 1 К А В Комментарии: Обе прямые лежат на правой грани Учитель математики Арапова Т. А.

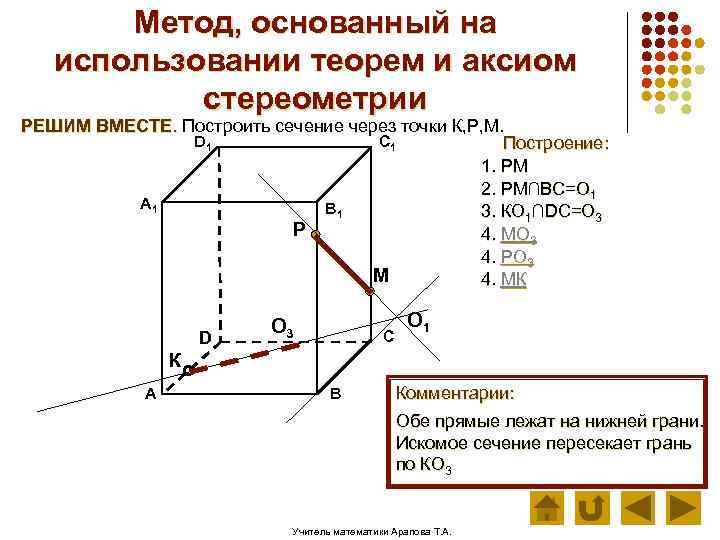Метод, основанный на использовании теорем и аксиом стереометрии РЕШИМ ВМЕСТЕ. Построить сечение через точки К, Р, М. D 1 C 1 Построение: 1. РМ 2. РМ∩ВС=О 1 А 1 В 1 3. КО 1∩DC=О 3 Р 4. МО 3 4. РО 3 М 4. МК D О 3 С О 1 К А В Комментарии: Обе прямые лежат на нижней грани. Искомое сечение пересекает грань по КО 3 Учитель математики Арапова Т. А.

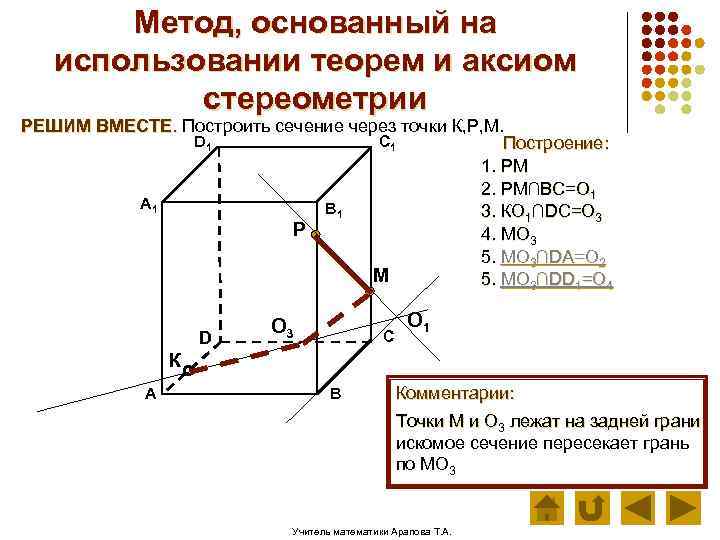Метод, основанный на использовании теорем и аксиом стереометрии РЕШИМ ВМЕСТЕ. Построить сечение через точки К, Р, М. D 1 C 1 Построение: 1. РМ 2. РМ∩ВС=О 1 А 1 В 1 3. КО 1∩DC=О 3 Р 4. МО 3 5. МО 3∩DА=О 2 М 5. МО 3∩DD 1=О 4 D О 3 С О 1 К А В Комментарии: Точки М и О 3 лежат на задней грани искомое сечение пересекает грань по МО 3 Учитель математики Арапова Т. А.

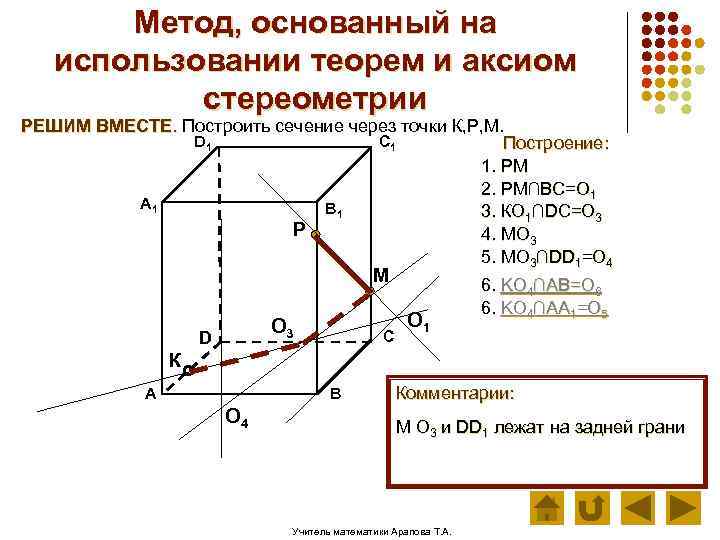Метод, основанный на использовании теорем и аксиом стереометрии РЕШИМ ВМЕСТЕ. Построить сечение через точки К, Р, М. D 1 C 1 Построение: 1. РМ 2. РМ∩ВС=О 1 А 1 В 1 3. КО 1∩DC=О 3 Р 4. МО 3 5. МО 3∩DD 1=О 4 М О 3 D С О 1 6. KО 4∩AB=О 6 6. KО 4∩AA 1=О 5 К А В О 4 Комментарии: М О 3 и DD 1 лежат на задней грани Учитель математики Арапова Т. А.

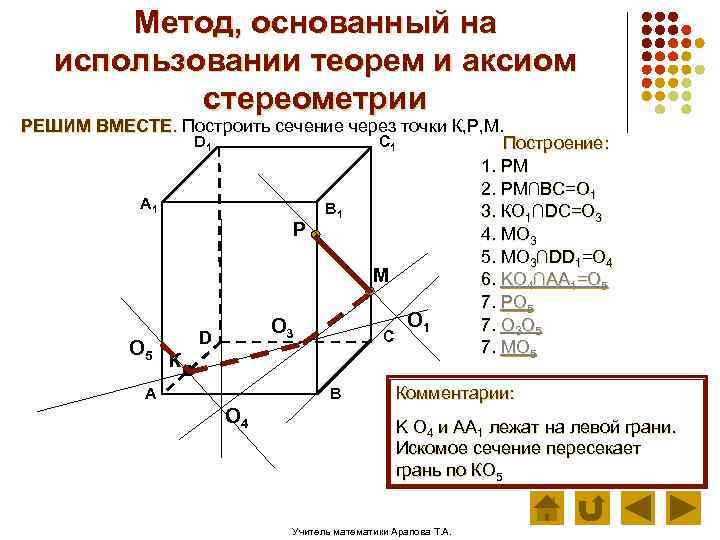Метод, основанный на использовании теорем и аксиом стереометрии РЕШИМ ВМЕСТЕ. Построить сечение через точки К, Р, М. D 1 C 1 Построение: 1. РМ 2. РМ∩ВС=О 1 А 1 В 1 3. КО 1∩DC=О 3 Р 4. МО 3 5. МО 3∩DD 1=О 4 М 6. KО 4∩AA 1=О 5 7. РО 5 О 1 7. О 3 О 5 О 3 С D 7. МО 5 К А В О 4 Комментарии: K О 4 и AA 1 лежат на левой грани. Искомое сечение пересекает грань по КО 5 Учитель математики Арапова Т. А.

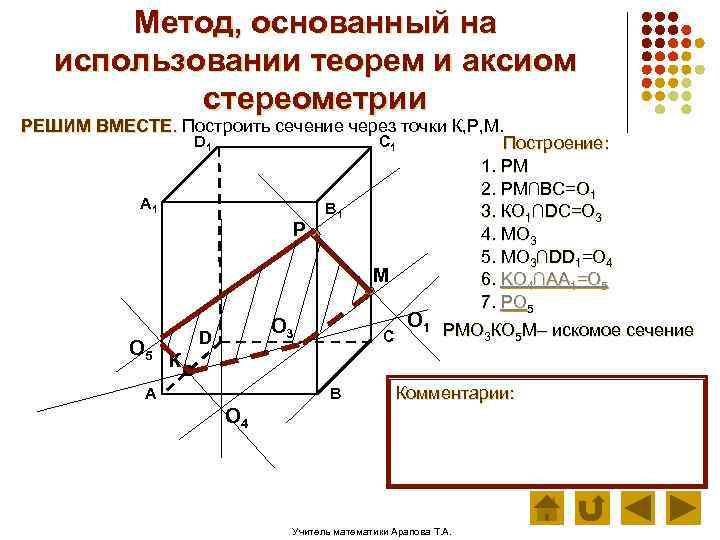Метод, основанный на использовании теорем и аксиом стереометрии РЕШИМ ВМЕСТЕ. Построить сечение через точки К, Р, М. D 1 C 1 Построение: 1. РМ 2. РМ∩ВС=О 1 А 1 В 1 3. КО 1∩DC=О 3 Р 4. МО 3 5. МО 3∩DD 1=О 4 М 6. KО 4∩AA 1=О 5 7. РО 5 О 3 D С О 1 РМО КО М– искомое сечение 3 5 К А В Комментарии: О 4 Учитель математики Арапова Т. А.

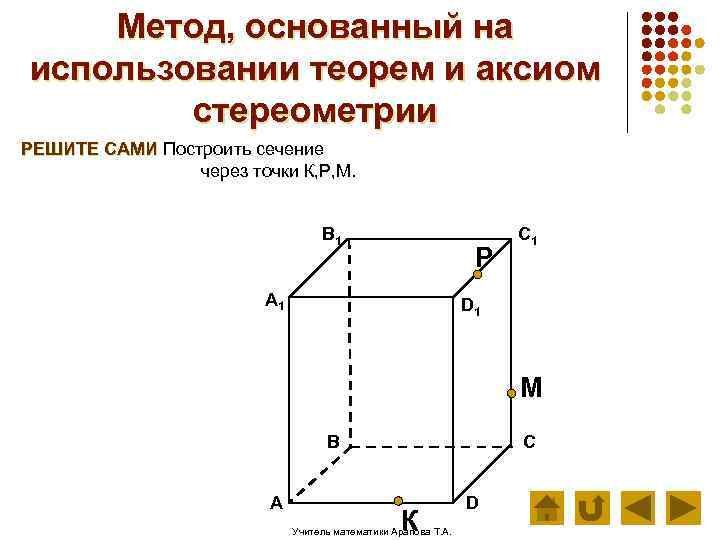Метод, основанный на использовании теорем и аксиом стереометрии РЕШИТЕ САМИ Построить сечение через точки К, Р, М. В 1 Р А 1 C 1 D 1 М В А С К Учитель математики Арапова Т. А. D

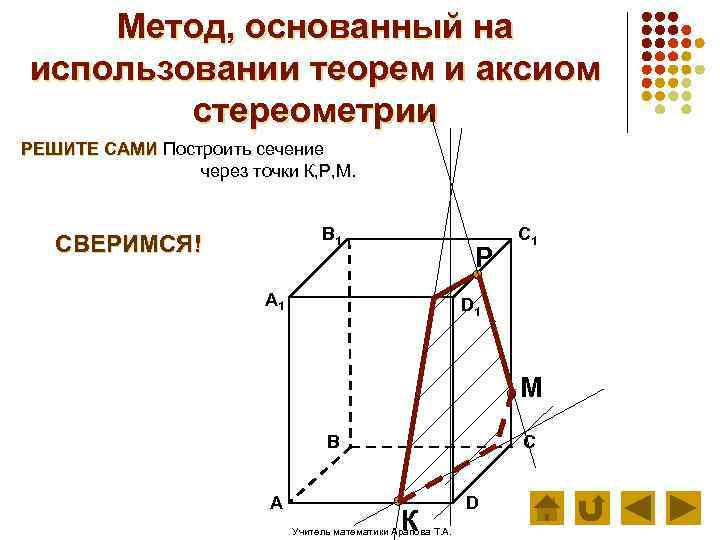Метод, основанный на использовании теорем и аксиом стереометрии РЕШИТЕ САМИ Построить сечение через точки К, Р, М. В 1 СВЕРИМСЯ! Р А 1 C 1 D 1 М В А С К Учитель математики Арапова Т. А. D

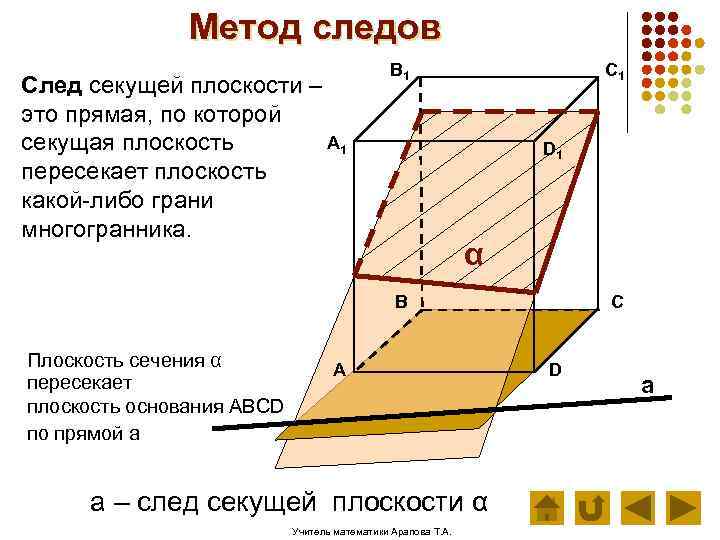Метод следов След секущей плоскости – это прямая, по которой А 1 секущая плоскость пересекает плоскость какой-либо грани многогранника. В 1 C 1 D 1 α В Плоскость сечения α пересекает плоскость основания АВСD по прямой а А а – след секущей плоскости α Учитель математики Арапова Т. А. С D а

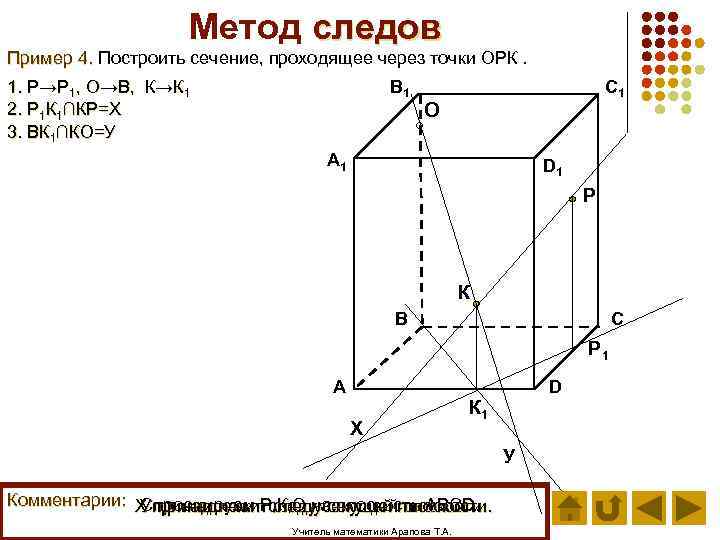Метод следов Пример 4. Построить сечение, проходящее через точки ОРК. В 1 1. Р→Р 1, О→В, К→К 1 2. Р 1 К 1∩КР=Х 3. ВК 1∩КО=У C 1 О А 1 D 1 Р К В С Р 1 А Х D К 1 У Комментарии: Х принадлежит. Р, К, О на плоскость АВСD. Спроецируем следу секущей плоскости. У принадлежит следу секущей плоскости. Учитель математики Арапова Т. А.

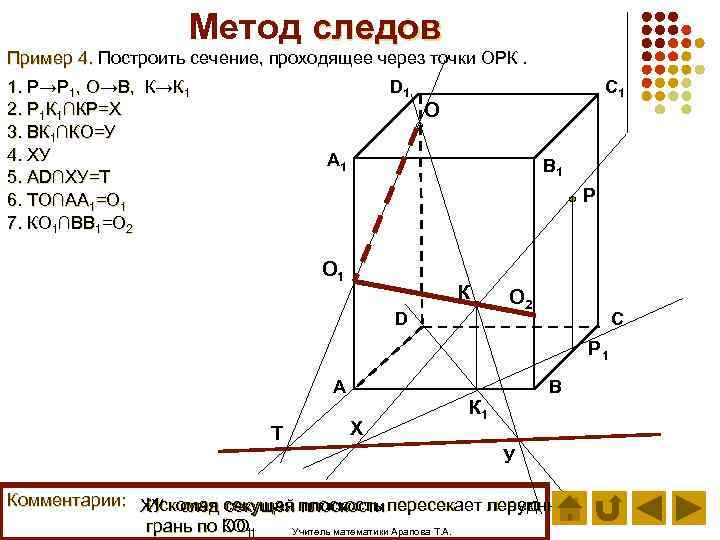Метод следов Пример 4. Построить сечение, проходящее через точки ОРК. D 1 1. Р→Р 1, О→В, К→К 1 2. Р 1 К 1∩КР=Х 3. ВК 1∩КО=У 4. ХУ 5. АD∩ХУ=Т 6. ТО∩АА 1=О 1 7. КО 1∩ВВ 1=О 2 C 1 О А 1 B 1 Р О 1 К D О 2 С Р 1 А Т Х В К 1 У Комментарии: ХУ - след секущая плоскость пересекает левую Искомая секущей плоскости переднюю грань по ОО 11 КО Учитель математики Арапова Т. А.

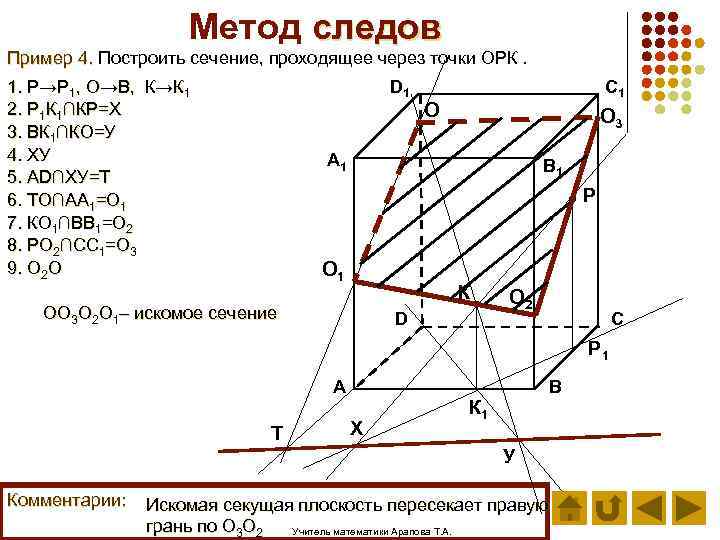Метод следов Пример 4. Построить сечение, проходящее через точки ОРК. D 1 1. Р→Р 1, О→В, К→К 1 2. Р 1 К 1∩КР=Х 3. ВК 1∩КО=У 4. ХУ 5. АD∩ХУ=Т 6. ТО∩АА 1=О 1 7. КО 1∩ВВ 1=О 2 8. РО 2∩СС 1=О 3 9. О 2 О C 1 О О 3 А 1 B 1 Р О 1 К ОО 3 О 2 О 1– искомое сечение D О 2 С Р 1 А Т Х В К 1 У Комментарии: Искомая секущая плоскость пересекает правую грань по О 3 О 2 Учитель математики Арапова Т. А.

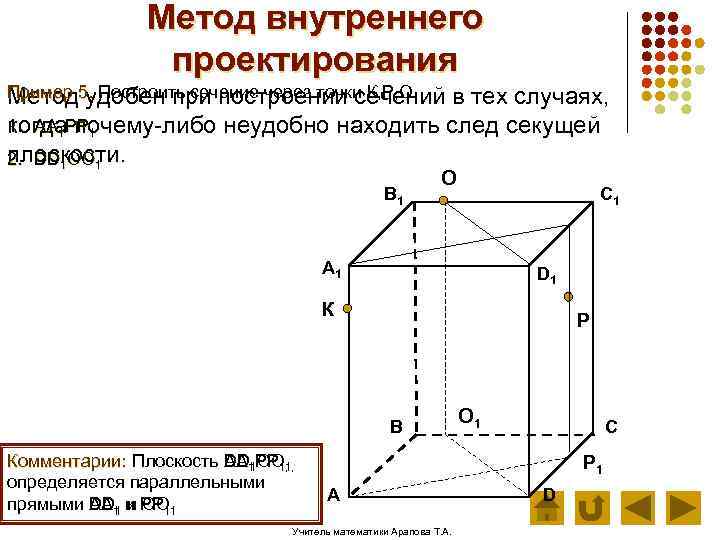Метод внутреннего проектирования Пример 5. Построить сечение через точки К, Р, О. Метод удобен при построении сечений в тех случаях, 1. АА 1 РР 1 когда почему-либо неудобно находить след секущей плоскости. 2. DD 1 ОО 1 В 1 О C 1 А 1 D 1 К Р В Комментарии: Плоскость АА 1 РР 1, DD 1 ОО 1, определяется параллельными прямыми АА 1 и РР 11 DD 1 и OO О 1 С Р 1 А Учитель математики Арапова Т. А. D

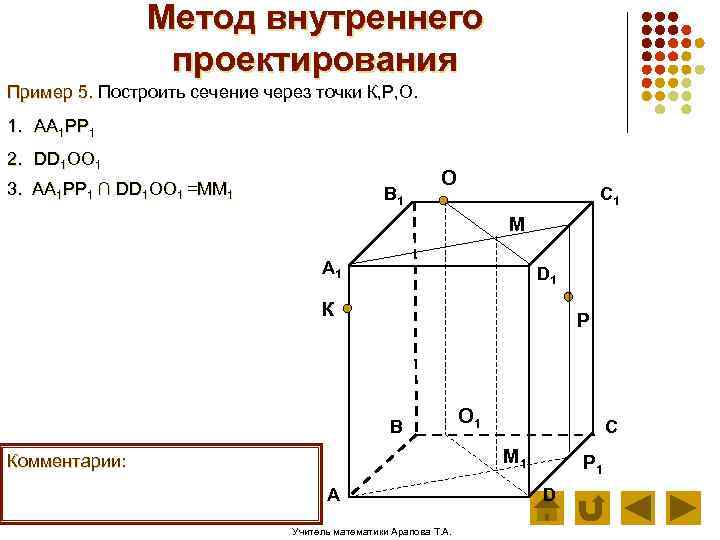Метод внутреннего проектирования Пример 5. Построить сечение через точки К, Р, О. 1. АА 1 РР 1 2. DD 1 ОО 1 3. АА 1 РР 1 ∩ DD 1 ОО 1 =ММ 1 В 1 О C 1 М А 1 D 1 К Р В О 1 С М 1 Комментарии: А Учитель математики Арапова Т. А. Р 1 D

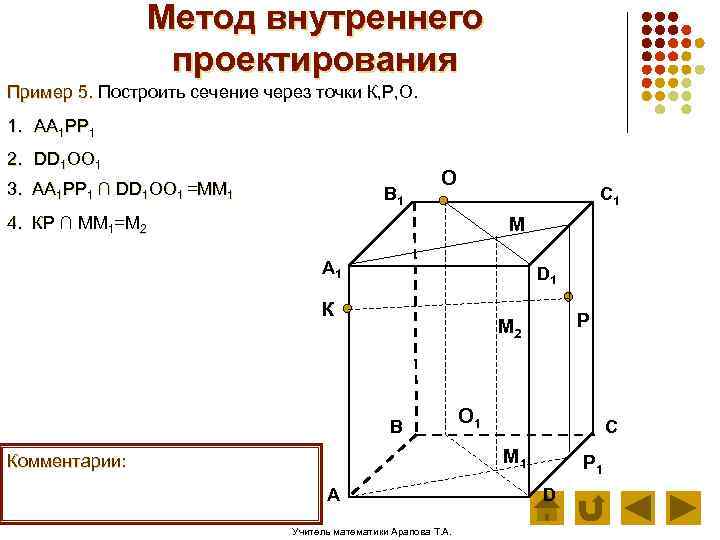Метод внутреннего проектирования Пример 5. Построить сечение через точки К, Р, О. 1. АА 1 РР 1 2. DD 1 ОО 1 3. АА 1 РР 1 ∩ DD 1 ОО 1 =ММ 1 В 1 О C 1 4. КР ∩ ММ 1=М 2 М А 1 D 1 К Р М 2 В О 1 С М 1 Комментарии: А Учитель математики Арапова Т. А. Р 1 D

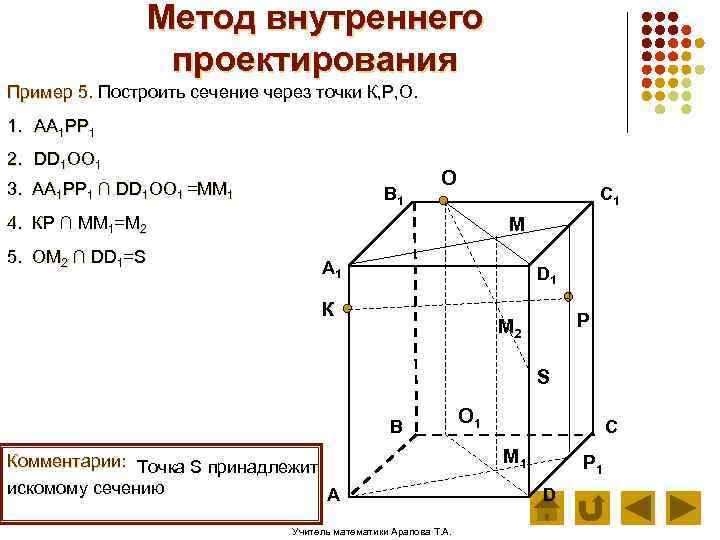Метод внутреннего проектирования Пример 5. Построить сечение через точки К, Р, О. 1. АА 1 РР 1 2. DD 1 ОО 1 3. АА 1 РР 1 ∩ DD 1 ОО 1 =ММ 1 В 1 О C 1 4. КР ∩ ММ 1=М 2 5. ОМ 2 ∩ DD 1=S М А 1 D 1 К Р М 2 S В Комментарии: Точка S принадлежит искомому сечению А Учитель математики Арапова Т. А. О 1 С М 1 Р 1 D

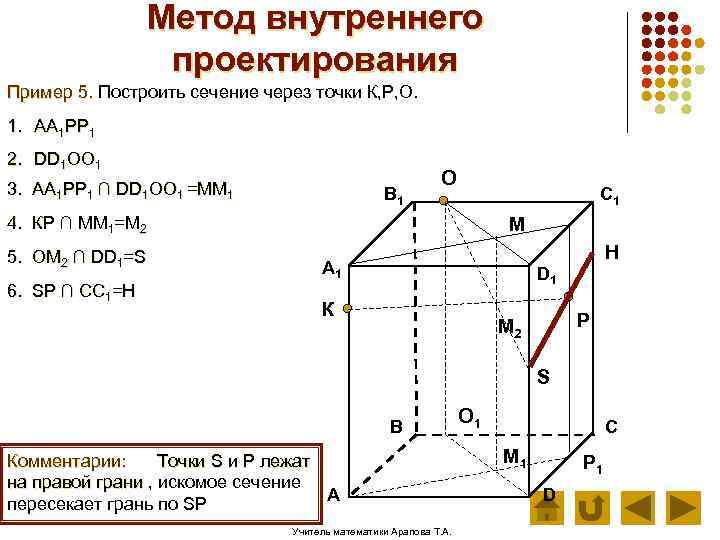Метод внутреннего проектирования Пример 5. Построить сечение через точки К, Р, О. 1. АА 1 РР 1 2. DD 1 ОО 1 3. АА 1 РР 1 ∩ DD 1 ОО 1 =ММ 1 В 1 О C 1 4. КР ∩ ММ 1=М 2 5. ОМ 2 ∩ DD 1=S 6. SP ∩ CC 1=H М H А 1 D 1 К Р М 2 S В Комментарии: Точки S и Р лежат на правой грани , искомое сечение А пересекает грань по SР Учитель математики Арапова Т. А. О 1 С М 1 Р 1 D

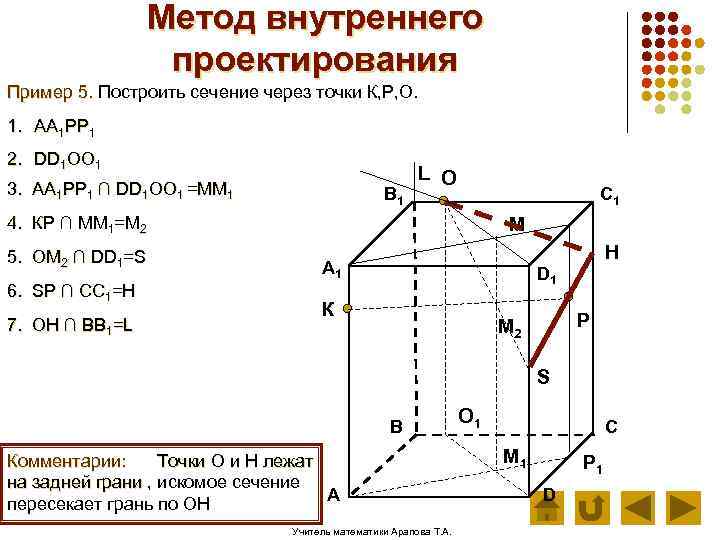Метод внутреннего проектирования Пример 5. Построить сечение через точки К, Р, О. 1. АА 1 РР 1 2. DD 1 ОО 1 3. АА 1 РР 1 ∩ DD 1 ОО 1 =ММ 1 В 1 L О C 1 4. КР ∩ ММ 1=М 2 5. ОМ 2 ∩ DD 1=S 6. SP ∩ CC 1=H 7. OH ∩ BB 1=L М H А 1 D 1 К Р М 2 S В Комментарии: Точки O и H лежат на задней грани , искомое сечение А пересекает грань по OH Учитель математики Арапова Т. А. О 1 С М 1 Р 1 D

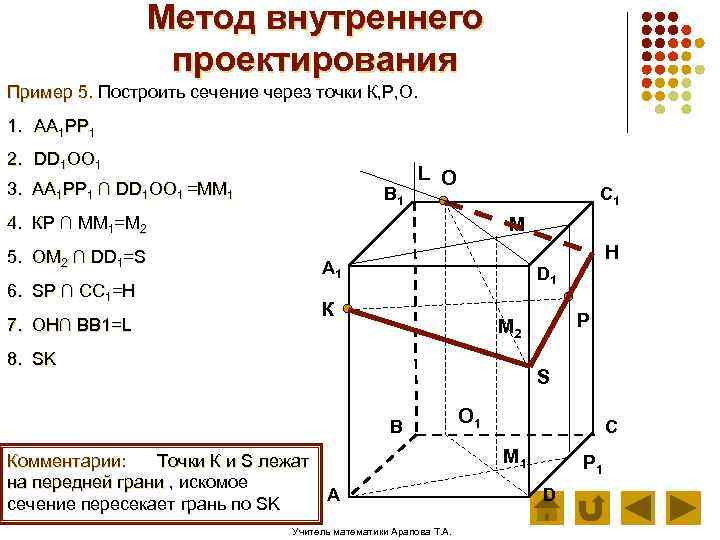Метод внутреннего проектирования Пример 5. Построить сечение через точки К, Р, О. 1. АА 1 РР 1 2. DD 1 ОО 1 3. АА 1 РР 1 ∩ DD 1 ОО 1 =ММ 1 В 1 L О C 1 4. КР ∩ ММ 1=М 2 5. ОМ 2 ∩ DD 1=S 6. SP ∩ CC 1=H 7. OH∩ BB 1=L М H А 1 D 1 К Р М 2 8. SK S В Комментарии: Точки К и S лежат на передней грани , искомое А сечение пересекает грань по SK Учитель математики Арапова Т. А. О 1 С М 1 Р 1 D

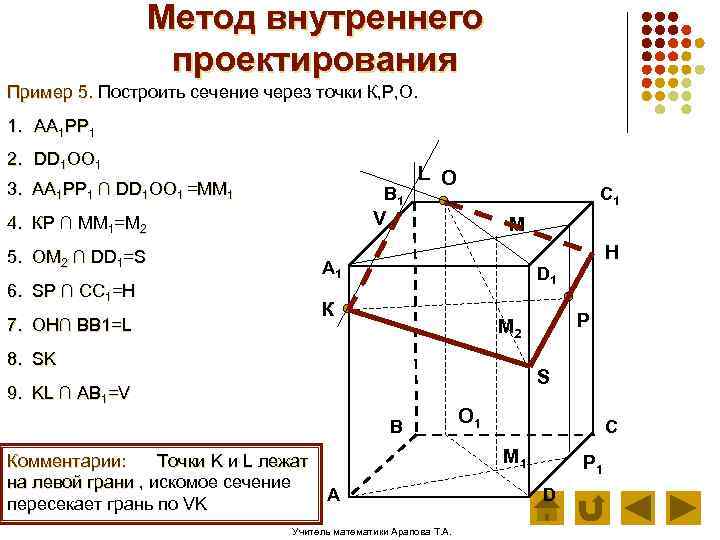Метод внутреннего проектирования Пример 5. Построить сечение через точки К, Р, О. 1. АА 1 РР 1 2. DD 1 ОО 1 3. АА 1 РР 1 ∩ DD 1 ОО 1 =ММ 1 В 1 L О C 1 V 4. КР ∩ ММ 1=М 2 5. ОМ 2 ∩ DD 1=S М H А 1 6. SP ∩ CC 1=H D 1 К 7. OH∩ BB 1=L Р М 2 8. SK S 9. KL ∩ AB 1=V В Комментарии: Точки K и L лежат на левой грани , искомое сечение пересекает грань по VK О 1 С М 1 А Учитель математики Арапова Т. А. Р 1 D

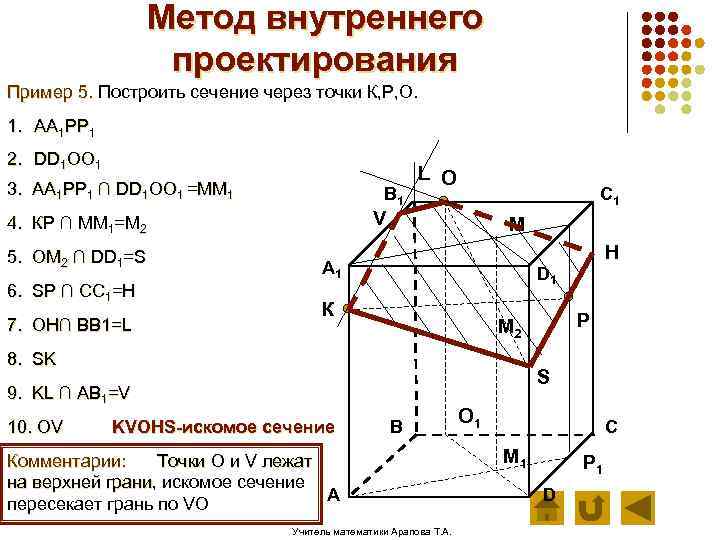Метод внутреннего проектирования Пример 5. Построить сечение через точки К, Р, О. 1. АА 1 РР 1 2. DD 1 ОО 1 3. АА 1 РР 1 ∩ DD 1 ОО 1 =ММ 1 В 1 6. SP ∩ CC 1=H 7. OH∩ BB 1=L C 1 V 4. КР ∩ ММ 1=М 2 5. ОМ 2 ∩ DD 1=S L О М H А 1 D 1 К 8. SK S 9. KL ∩ AB 1=V 10. OV Р М 2 KVOHS-искомое сечение В Комментарии: Точки O и V лежат на верхней грани, искомое сечение грани А пересекает грань по VO Учитель математики Арапова Т. А. О 1 С М 1 Р 1 D

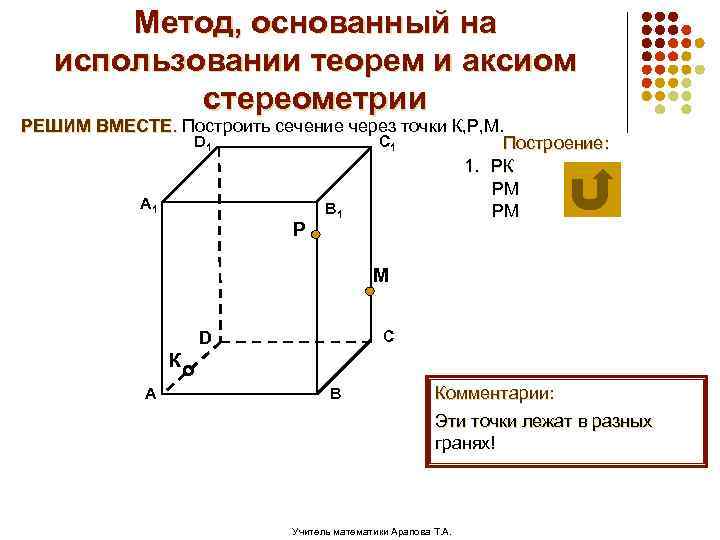Метод, основанный на использовании теорем и аксиом стереометрии РЕШИМ ВМЕСТЕ. Построить сечение через точки К, Р, М. D 1 C 1 Построение: 1. РК РМ А 1 В 1 РМ Р М С D К А В Комментарии: Эти точки лежат в разных гранях! Учитель математики Арапова Т. А.

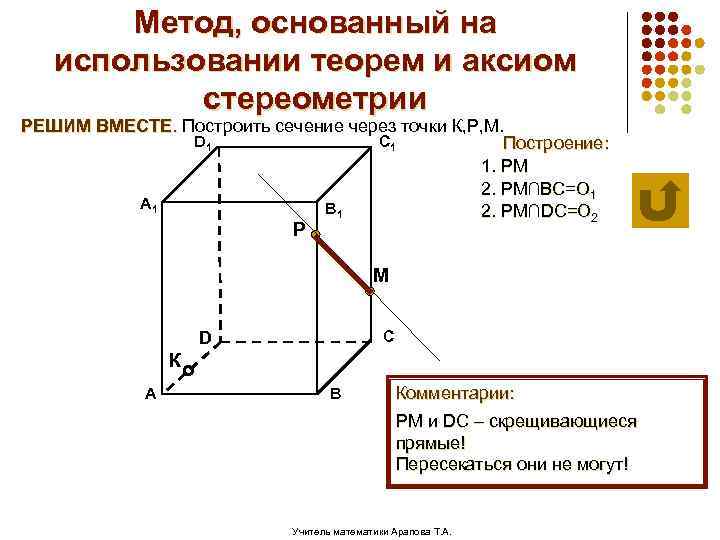Метод, основанный на использовании теорем и аксиом стереометрии РЕШИМ ВМЕСТЕ. Построить сечение через точки К, Р, М. D 1 C 1 Построение: 1. РМ 2. РМ∩ВС=О 1 А 1 В 1 2. РМ∩DС=О 2 Р М С D К А В Комментарии: РМ и DС – скрещивающиеся прямые! Пересекаться они не могут! Учитель математики Арапова Т. А.

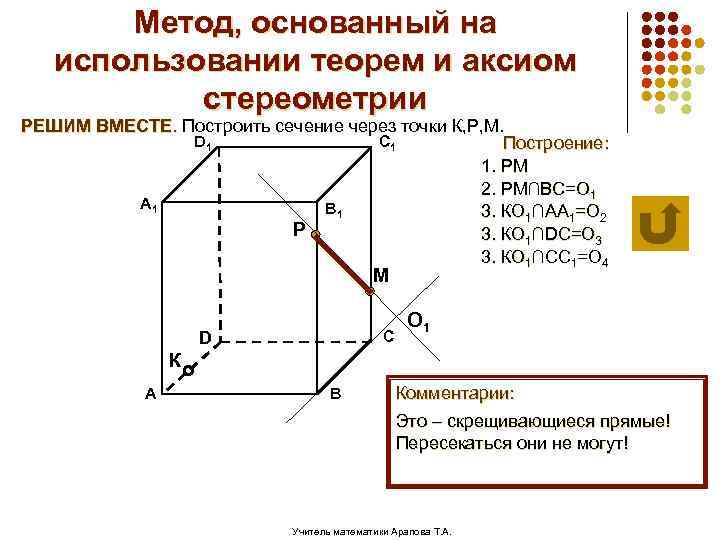Метод, основанный на использовании теорем и аксиом стереометрии РЕШИМ ВМЕСТЕ. Построить сечение через точки К, Р, М. D 1 C 1 Построение: 1. РМ 2. РМ∩ВС=О 1 А 1 В 1 3. КО 1∩АА 1=О 2 Р 3. КО 1∩DC=О 3 3. КО 1∩CC 1=О 4 М С D О 1 К А В Комментарии: Это – скрещивающиеся прямые! Пересекаться они не могут! Учитель математики Арапова Т. А.

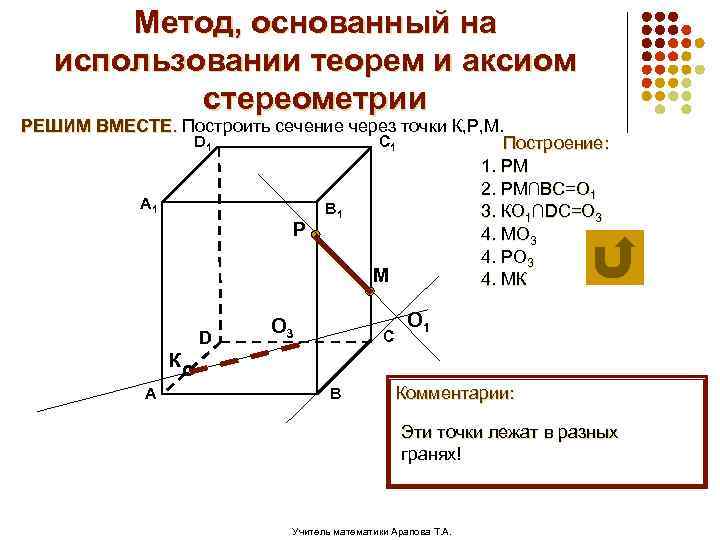Метод, основанный на использовании теорем и аксиом стереометрии РЕШИМ ВМЕСТЕ. Построить сечение через точки К, Р, М. D 1 C 1 Построение: 1. РМ 2. РМ∩ВС=О 1 А 1 В 1 3. КО 1∩DC=О 3 Р 4. МО 3 4. РО 3 М 4. МК D О 3 С О 1 К А В Комментарии: Эти точки лежат в разных гранях! Учитель математики Арапова Т. А.

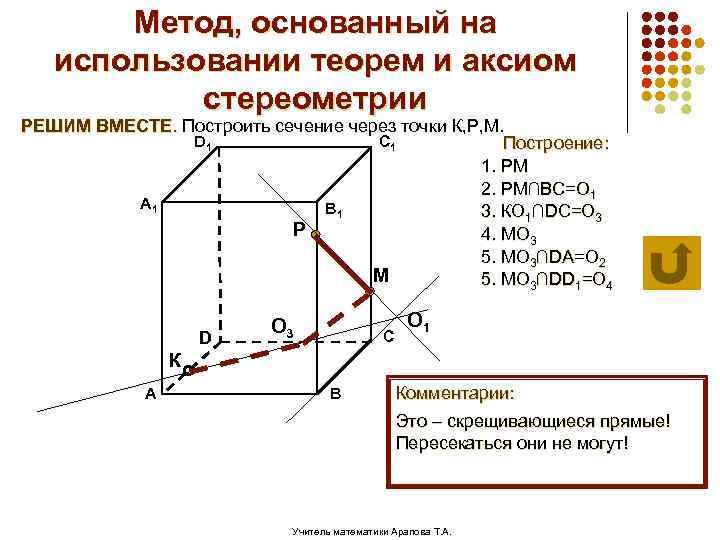Метод, основанный на использовании теорем и аксиом стереометрии РЕШИМ ВМЕСТЕ. Построить сечение через точки К, Р, М. D 1 C 1 Построение: 1. РМ 2. РМ∩ВС=О 1 А 1 В 1 3. КО 1∩DC=О 3 Р 4. МО 3 5. МО 3∩DА=О 2 М 5. МО 3∩DD 1=О 4 D О 3 С О 1 К А В Комментарии: Это – скрещивающиеся прямые! Пересекаться они не могут! Учитель математики Арапова Т. А.

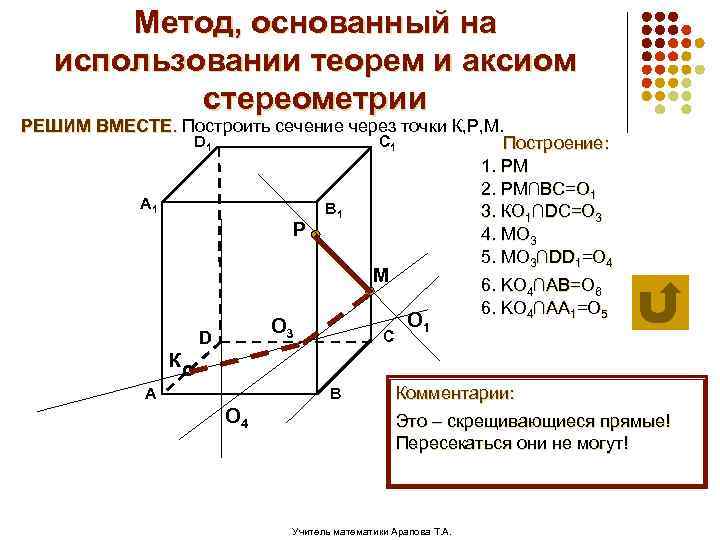Метод, основанный на использовании теорем и аксиом стереометрии РЕШИМ ВМЕСТЕ. Построить сечение через точки К, Р, М. D 1 C 1 Построение: 1. РМ 2. РМ∩ВС=О 1 А 1 В 1 3. КО 1∩DC=О 3 Р 4. МО 3 5. МО 3∩DD 1=О 4 М О 3 D С О 1 6. KО 4∩AB=О 6 6. KО 4∩AA 1=О 5 К А В О 4 Комментарии: Это – скрещивающиеся прямые! Пересекаться они не могут! Учитель математики Арапова Т. А.

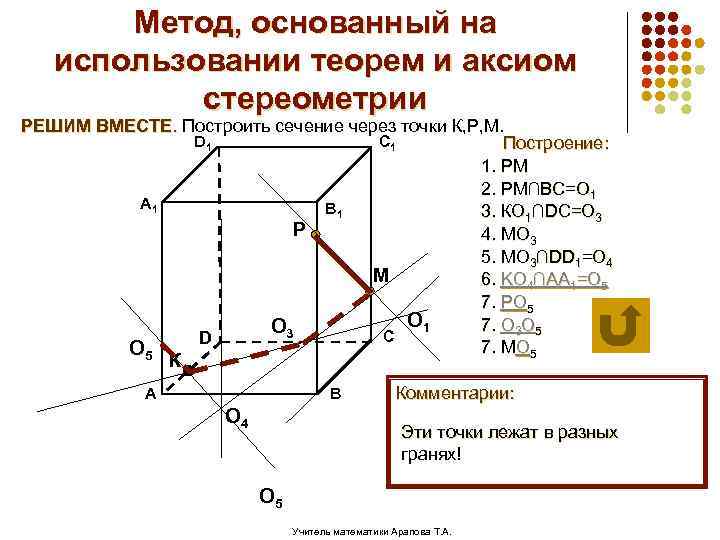Метод, основанный на использовании теорем и аксиом стереометрии РЕШИМ ВМЕСТЕ. Построить сечение через точки К, Р, М. D 1 C 1 Построение: 1. РМ 2. РМ∩ВС=О 1 А 1 В 1 3. КО 1∩DC=О 3 Р 4. МО 3 5. МО 3∩DD 1=О 4 М 6. KО 4∩AA 1=О 5 7. РО 5 О 1 7. О 3 О 5 О 3 С D 7. МО 5 К А В О 4 Комментарии: Эти точки лежат в разных гранях! О 5 Учитель математики Арапова Т. А.