1ab79cec5ada9f3b250b7fab1487237d.ppt
- Количество слайдов: 11

Построение плоских сечений в призмах і пирамидах Разработал учитель математики и информатики Дружбинского УВК: ОШ І-ІІІ ст. - ДУЗ А. В. Якушев А. В.

Если две пространственные фигуры имеют общие точки, то можно говорить, что эта общая часть является сечением одной из этих фигур другой. Задачи нахождения сечения одной фигуры другой является предметом изучения геометрии и черчения, и используется в практической сфере, в частности, в архитектуре и строительстве. В школьному курсе стереометрии изучаются свойства относительно простых фигур: многогранников (призмы, пирамиды), фигур вращения (цилиндр, конус, шар, сфера), но умение строить относительно несложные сечения этих фигур - является основой для построения более сложных сечений в будущем. Важным аспектом изучения стереометрии - формирование у ученика пространственного воображения. Построение сечений одной фигуры другой содержит в себе не только развивающую, практическую функции, но, і позволяет формовать это пространственное воображение, В этой презентации рассмотрены алгоритмы построения сечений призмы и пирамиды плоскостью (плоские сечения). Якушев А. В.

Виды проекций, которые используются в школьном курсе стереометрии для изображения фигур и построение плоских сечений Якушев А. В.
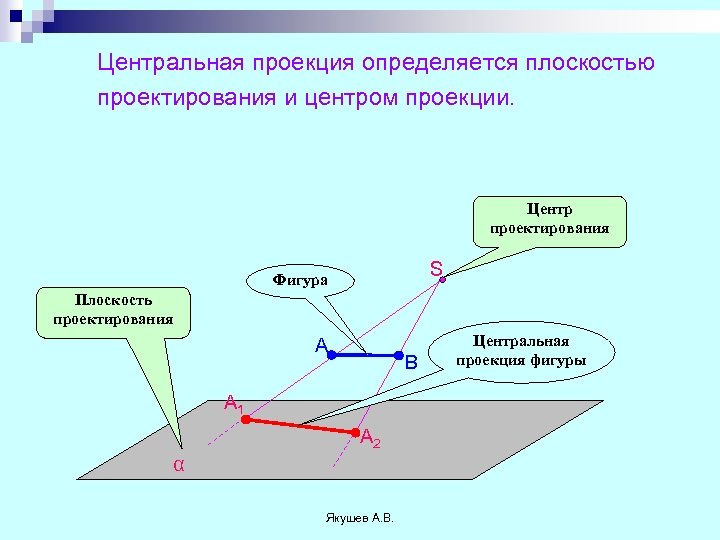
Центральная проекция определяется плоскостью проектирования и центром проекции. Центр проектирования S Фигура Плоскость проектирования A B A 1 A 2 α Якушев А. В. Центральная проекция фигуры

Параллельная проекция определяется: 1. 2. плоскостью проектирования; направлением проектирования – лучом, который пересекает плоскость проекций. Фигура Параллельная проекция фигуры Направление проектирования Плоскость проекций α Якушев А. В.
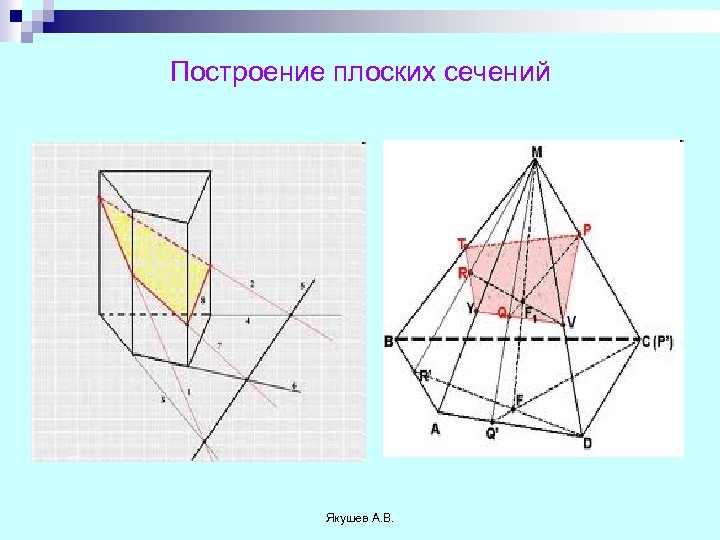
Построение плоских сечений Якушев А. В.
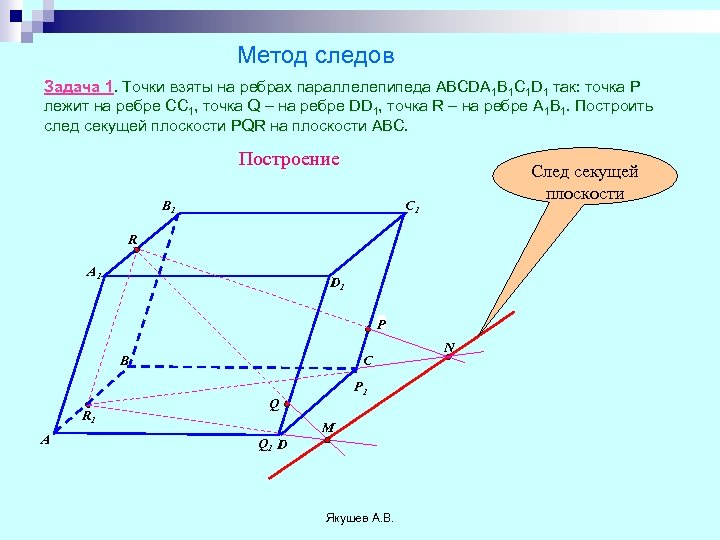
Метод следов Задача 1. Точки взяты на ребрах параллелепипеда ABCDA 1 B 1 C 1 D 1 так: точка P лежит на ребре CC 1, точка Q – на ребре DD 1, точка R – на ребре А 1 В 1. Построить след секущей плоскости PQR на плоскости АВС. Построение B 1 След секущей плоскости C 1 R A 1 D 1 P B R 1 A C P 1 Q M Q 1 D Якушев А. В. N
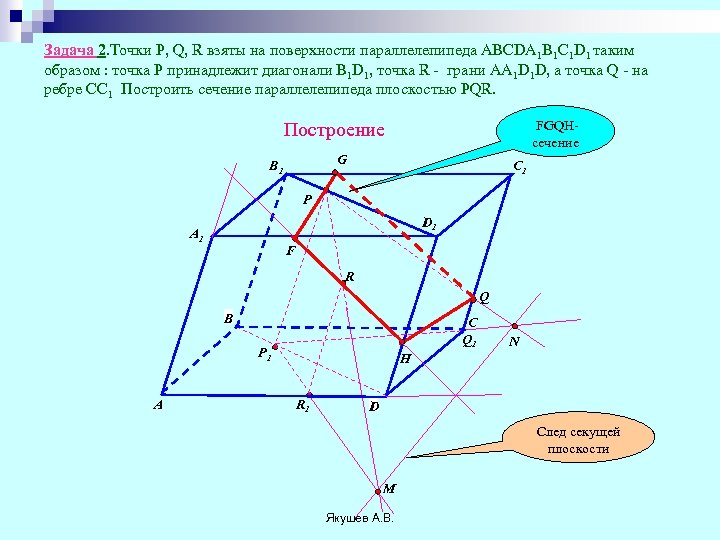
Задача 2. Точки Р, Q, R взяты на поверхности параллелепипеда ABCDA 1 B 1 C 1 D 1 таким образом : точка Р принадлежит диагонали B 1 D 1, точка R - грани AA 1 D 1 D, а точка Q - на ребре CC 1 Построить сечение параллелепипеда плоскостью PQR. FGQHсечение Построение G B 1 C 1 P D 1 A 1 F R Q B C Q 1 P 1 A N H R 1 D След секущей плоскости M Якушев А. В.
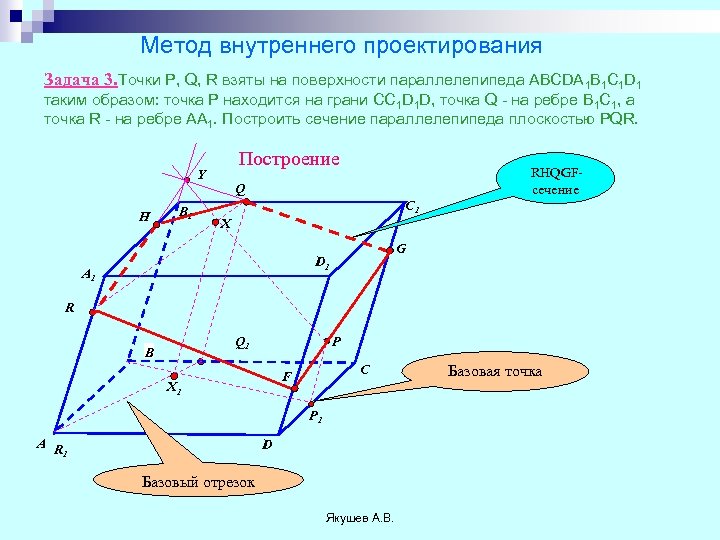
Метод внутреннего проектирования Задача 3. Точки P, Q, R взяты на поверхности параллелепипеда ABCDA 1 B 1 C 1 D 1 таким образом: точка Р находится на грани CC 1 D 1 D, точка Q - на ребре В 1 С 1, а точка R - на ребре АА 1. Построить сечение параллелепипеда плоскостью PQR. Построение Y H B 1 RHQGFсечение Q C 1 X G D 1 A 1 R Q 1 B P C F X 1 P 1 A R 1 D Базовый отрезок Якушев А. В. Базовая точка
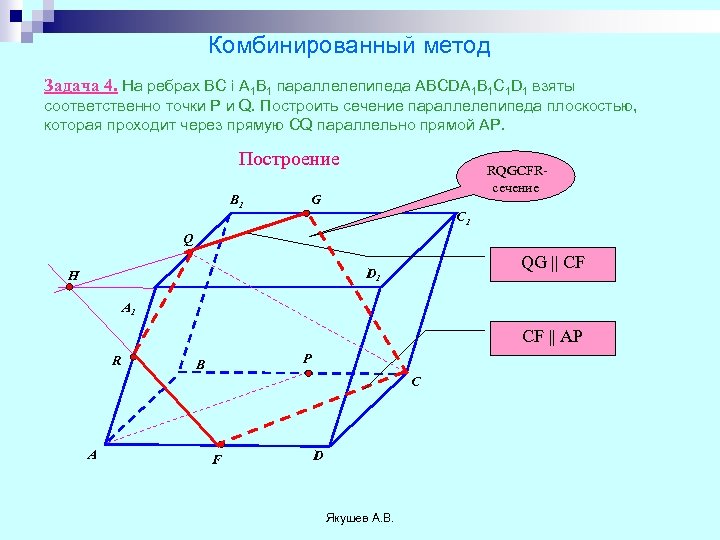
Комбинированный метод Задача 4. На ребрах ВС і А 1 В 1 параллелепипеда ABCDA 1 B 1 C 1 D 1 взяты соответственно точки Р и Q. Построить сечение параллелепипеда плоскостью, которая проходит через прямую CQ параллельно прямой АP. Построение B 1 RQGCFRсечение G C 1 Q QG || CF D 1 H A 1 CF || AP R P B C A F D Якушев А. В.
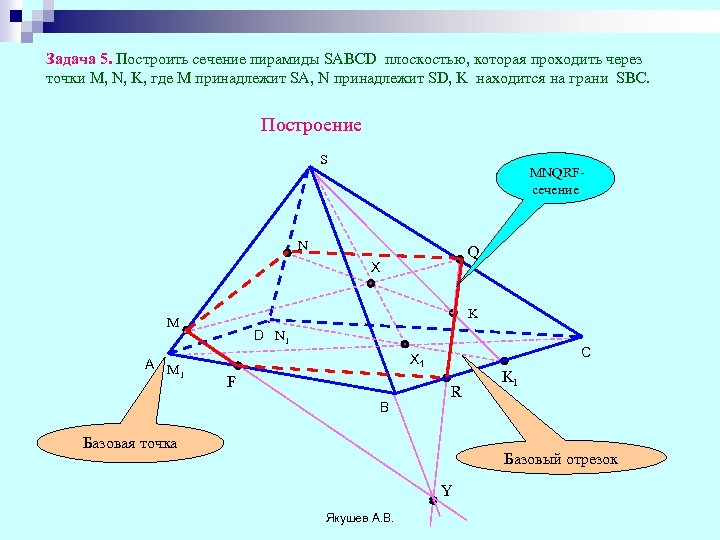
Задача 5. Построить сечение пирамиды SABCD плоскостью, которая проходить через точки M, N, K, где M принадлежит SA, N принадлежит SD, K находится на грани SBC. Построение S MNQRFсечение N Q X K M A M 1 D N 1 C X 1 F B R Базовая точка K 1 Базовый отрезок Y Якушев А. В.
1ab79cec5ada9f3b250b7fab1487237d.ppt