— построение линейного угла данного двугранного угла

- построение линейного угла данного двугранного угла.

• Построение линейного угла данного двугранного угла.

научиться построению линейного угла данного двугранного угла. üполучить необходимую информацию; üпроанализировать полученную информацию; üприменить теорию на практике; оценить свою деятельность.

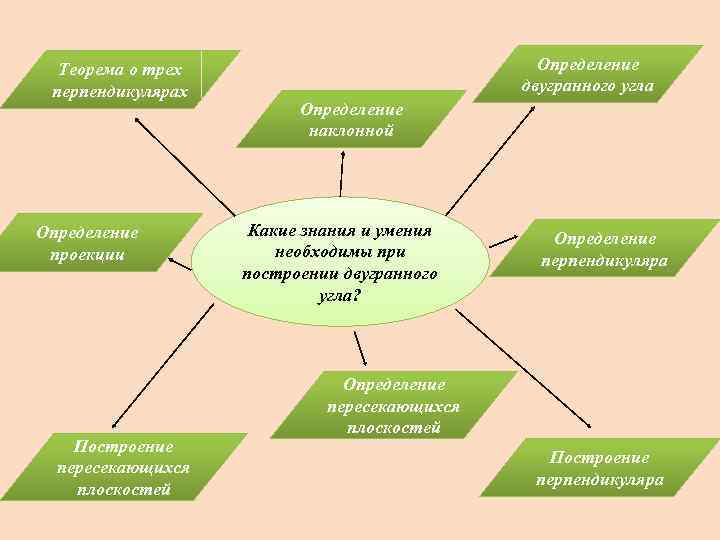Теорема о трех перпендикулярах Определение проекции Построение пересекающихся плоскостей Определение двугранного угла Определение наклонной Какие знания и умения необходимы при построении двугранного угла? Определение перпендикуляра Определение пересекающихся плоскостей Построение перпендикуляра

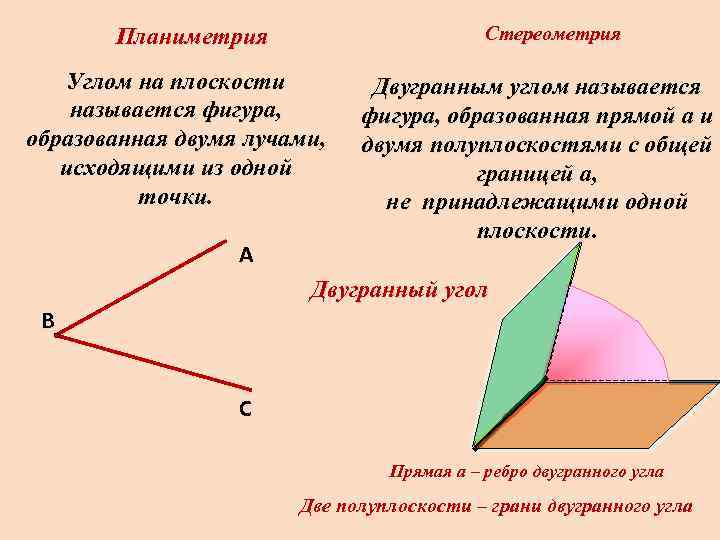Стереометрия Планиметрия Углом на плоскости называется фигура, образованная двумя лучами, исходящими из одной точки. А Двугранным углом называется фигура, образованная прямой a и двумя полуплоскостями с общей границей a, не принадлежащими одной плоскости. Двугранный угол В С а Прямая a – ребро двугранного угла Две полуплоскости – грани двугранного угла

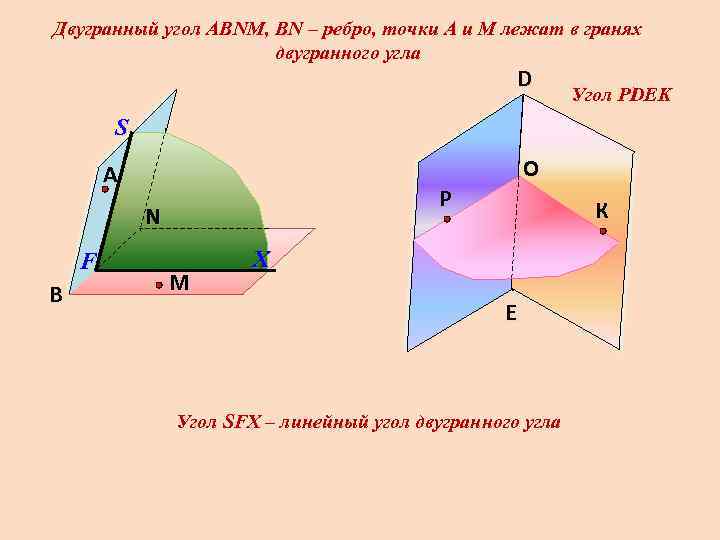Двугранный угол АВNМ, ВN – ребро, точки А и М лежат в гранях двугранного угла D Угол РDEK S А Р N F В O M К X E Угол SFX – линейный угол двугранного угла

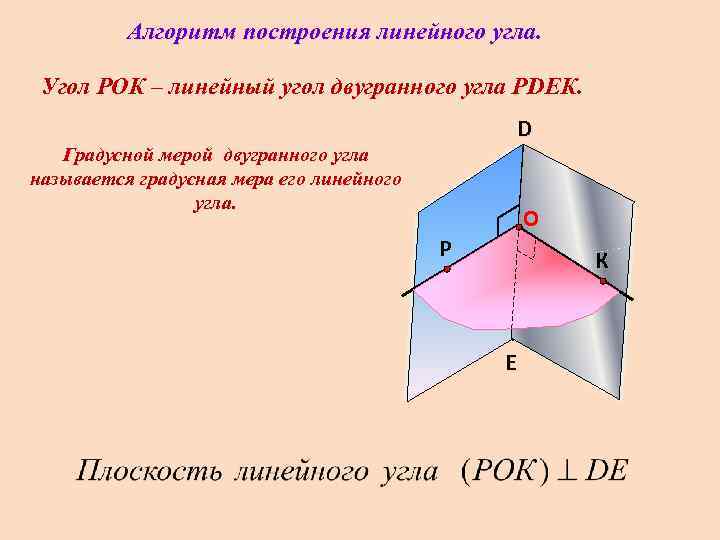Алгоритм построения линейного угла. Угол РОК – линейный угол двугранного угла РDEК. D Градусной мерой двугранного угла называется градусная мера его линейного угла. O Р К E

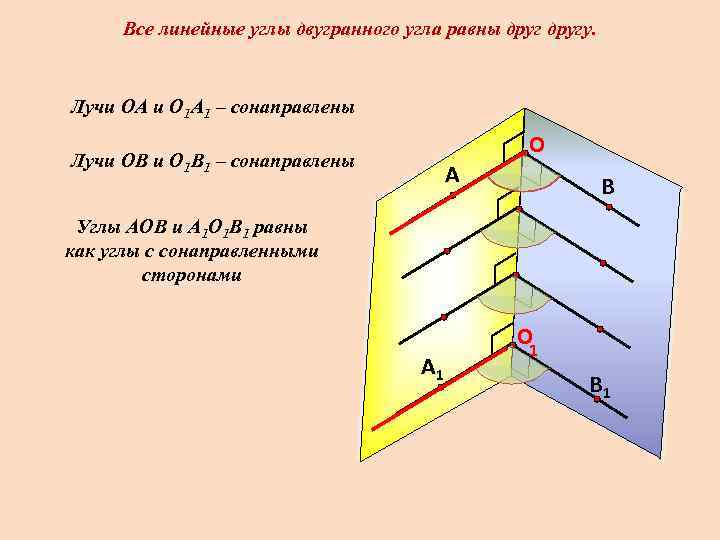Все линейные углы двугранного угла равны другу. Лучи ОА и О 1 А 1 – сонаправлены Лучи ОВ и О 1 В 1 – сонаправлены А O В Углы АОВ и А 1 О 1 В 1 равны как углы с сонаправленными сторонами А 1 O 1 В 1

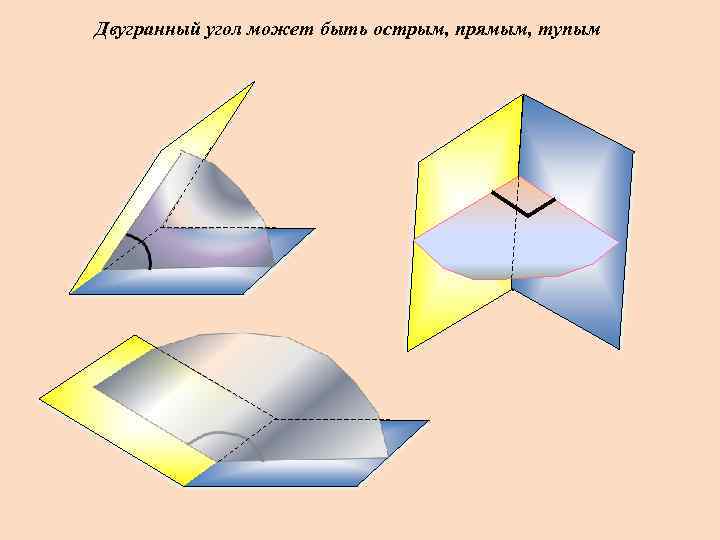Двугранный угол может быть острым, прямым, тупым

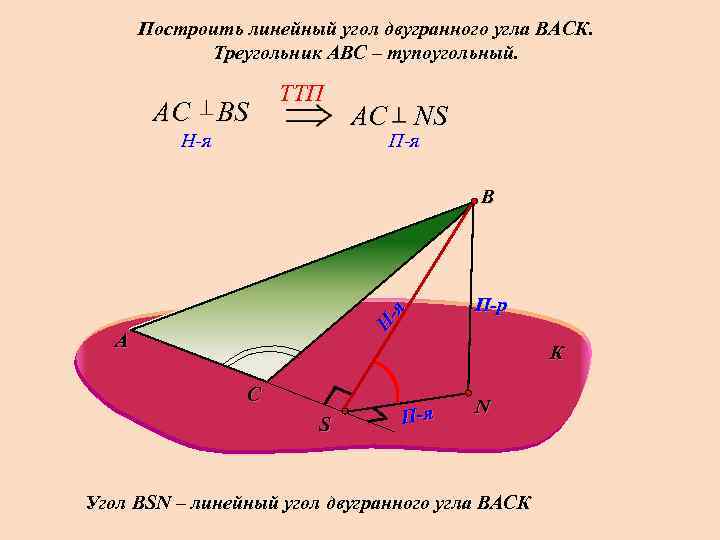Построить линейный угол двугранного угла ВАСК. Треугольник АВС – тупоугольный. АС ВS TTП H-я АС NS П-я Ня В А П-р К С S П-я N Угол ВSN – линейный угол двугранного угла ВАСК

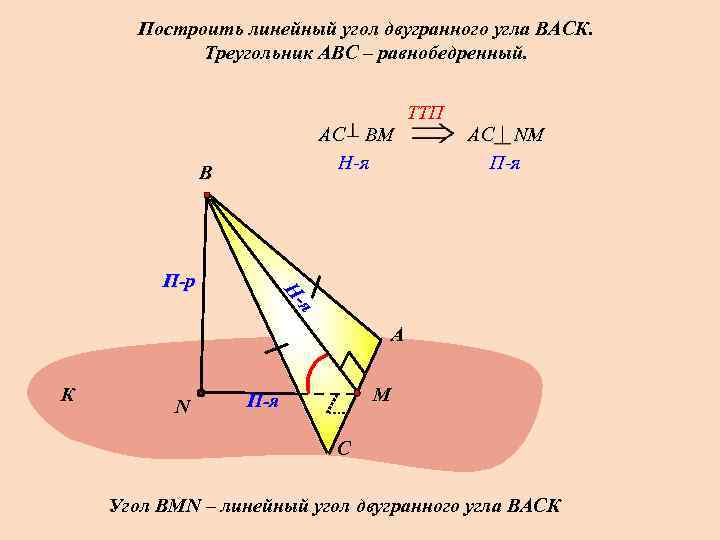Построить линейный угол двугранного угла ВАСК. Треугольник АВС – равнобедренный. TTП АС ВМ H-я В я --я Н Н П-р АС NМ П-я А К N M П-я С Угол ВMN – линейный угол двугранного угла ВАСК

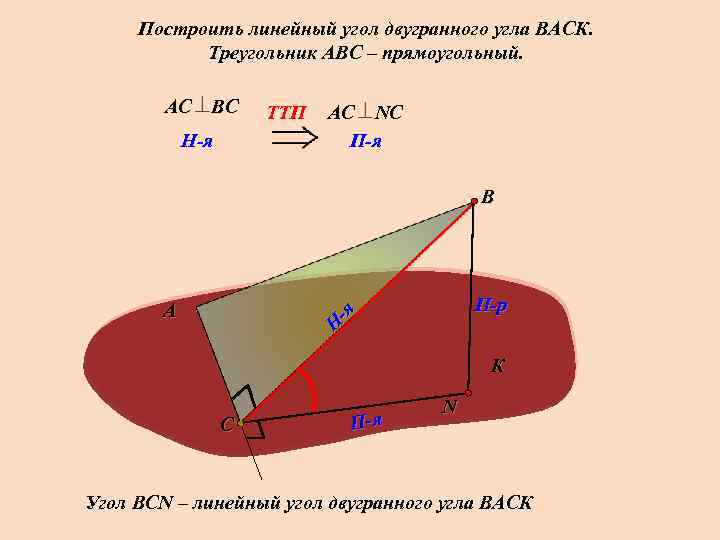Построить линейный угол двугранного угла ВАСК. Треугольник АВС – прямоугольный. АС ВС H-я TTП АС NС П-я В П-р Н -я А К С П-я N Угол ВСN – линейный угол двугранного угла ВАСК

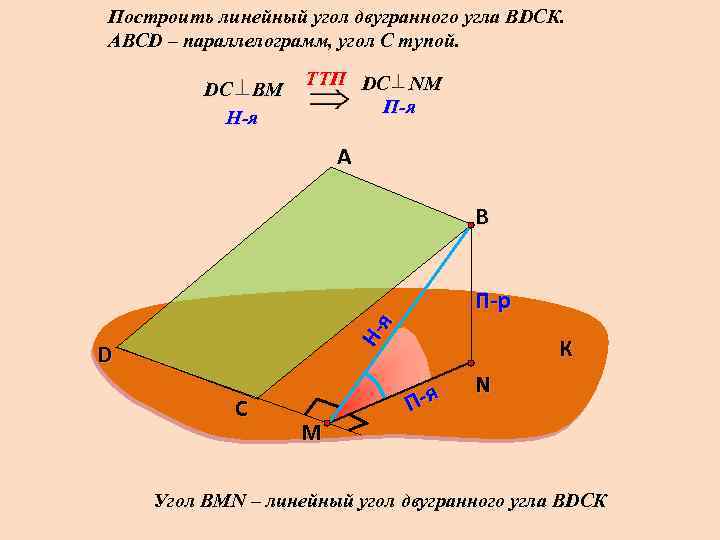Построить линейный угол двугранного угла ВDСК. АВСD – параллелограмм, угол С тупой. DС В M H-я TTП DС NM П-я А В Ня П-р D С M К П-я N Угол ВMN – линейный угол двугранного угла ВDСК

Построить линейный угол двугранного угла ВDСК. АВСD – прямоугольник. А DС N С П-я В D П-р Ня DС B С H-я TTП К С П-я N Угол ВСN – линейный угол двугранного угла ВАСК

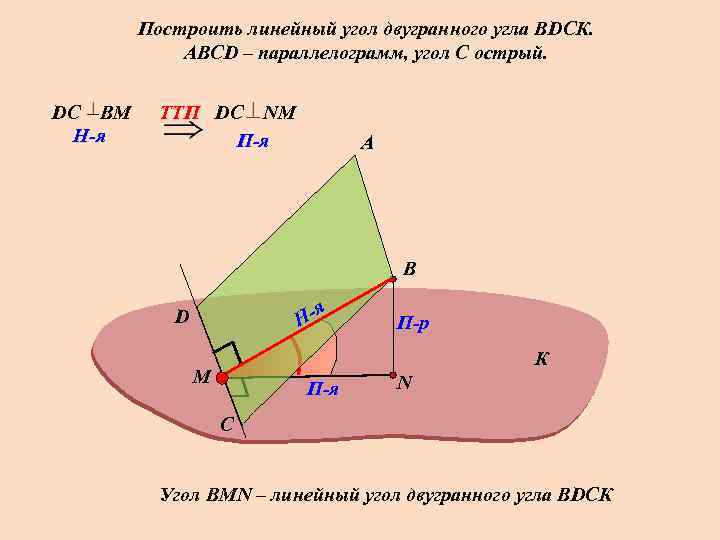Построить линейный угол двугранного угла ВDСК. АВСD – параллелограмм, угол С острый. DС В M H-я TTП DС NM П-я А В я Н- D П-р К M П-я N С Угол ВMN – линейный угол двугранного угла ВDСК

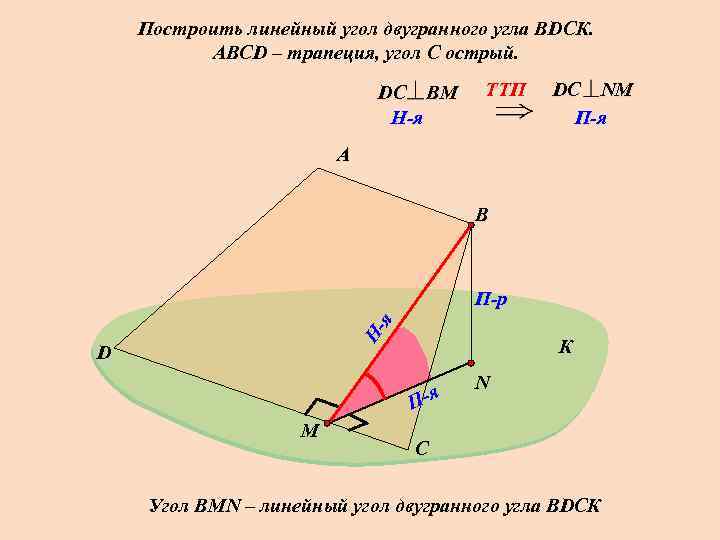Построить линейный угол двугранного угла ВDСК. АВСD – трапеция, угол С острый. DС В M H-я TTП DС NM П-я А В Ня П-р D К П-я M N С Угол ВMN – линейный угол двугранного угла ВDСК

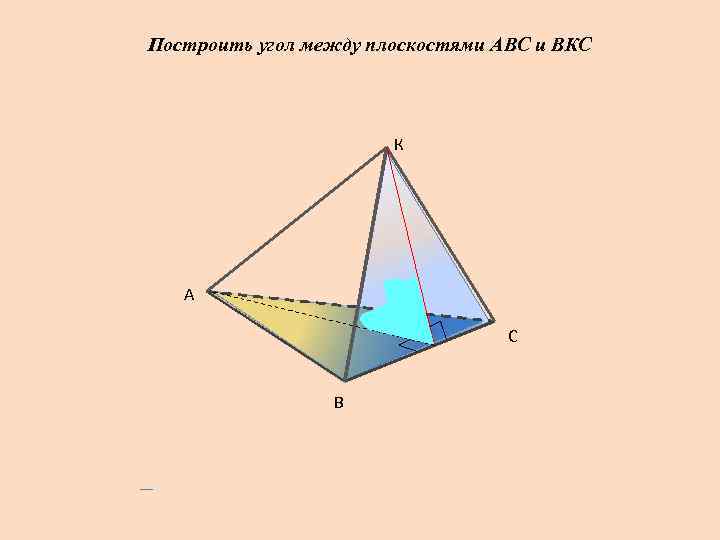Построить угол между плоскостями АВС и ВКС К А С В

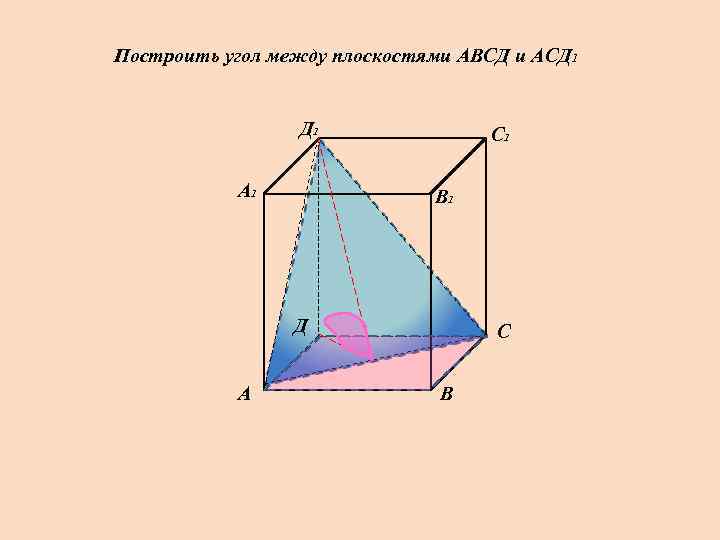Построить угол между плоскостями АВСД и АСД 1 А 1 С 1 В 1 Д А С В

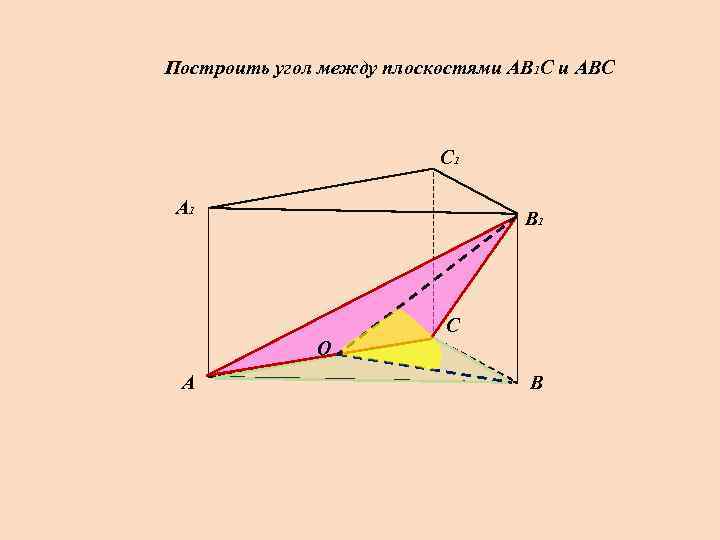Построить угол между плоскостями АВ 1 С и АВС С 1 А 1 В 1 С О А В

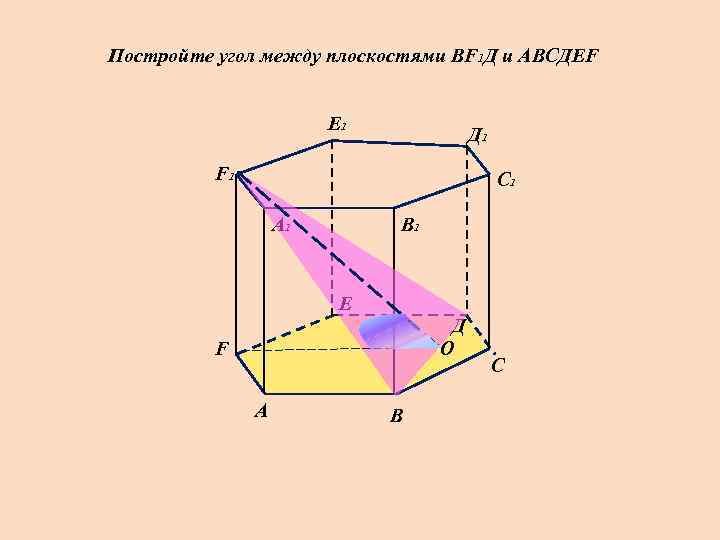Постройте угол между плоскостями ВF 1 Д и АВСДЕF Е 1 Д 1 F 1 С 1 А 1 В 1 Е Д О F А В С

Задача 1: В кубе A…D 1 найдите угол между плоскостями ABC и CDD 1. Задача 2: В кубе A…D 1 найдите угол между плоскостями ABC и CDA 1. Задача 3: Задача 4: Задача 5: Задача 6: В кубе A…D 1 найдите угол между плоскостями ABC и BDD 1. • В кубе A…D 1 найдите угол между плоскостями ACC 1 и BDD 1. В кубе A…D 1 найдите угол между плоскостями BC 1 D и BA 1 D. Неперпендикулярные плоскости и пересекаются по прямой МN. В плоскости из точки А проведен перпендикуляр АВ к прямой МN и из точки А проведен перпендикуляр АС к плоскости. Докажите, что угол АВС – линейный угол двугранного угла АМNC.

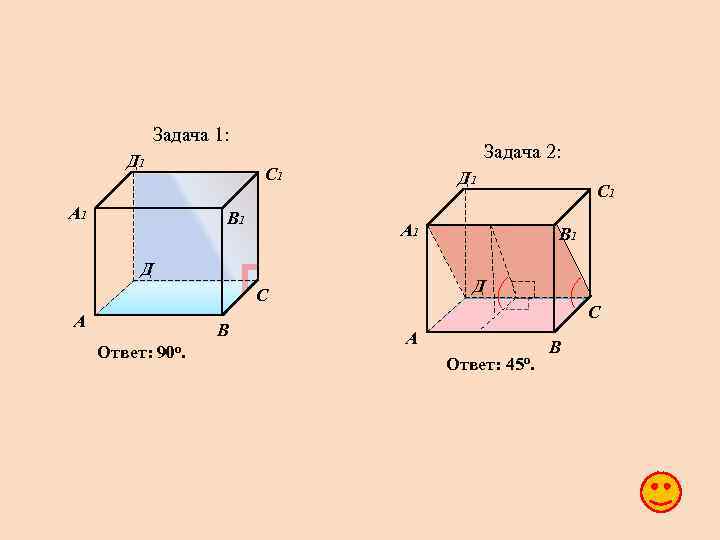Задача 1: Д 1 А 1 Задача 2: С 1 В 1 Д 1 А 1 Д В Ответ: 90 o. В 1 Д С А С 1 С А Ответ: 45 o. В

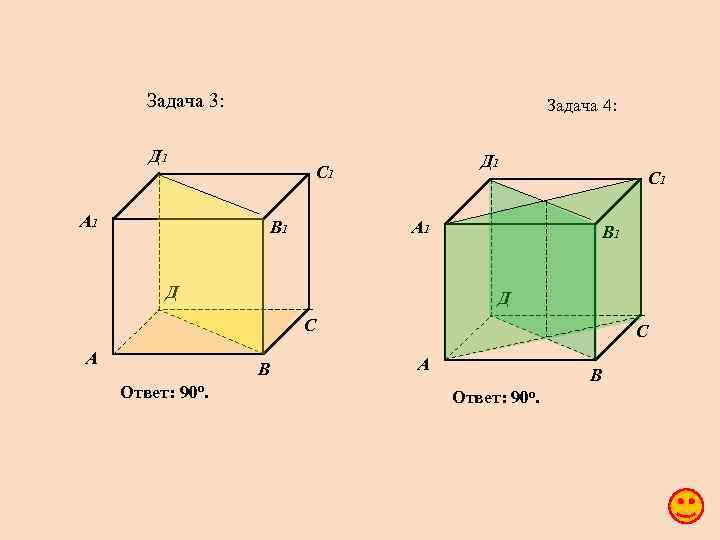Задача 3: Задача 4: Д 1 С 1 А 1 В 1 А 1 Д С 1 В 1 Д С А В Ответ: 90 o. С А В Ответ: 90 o.

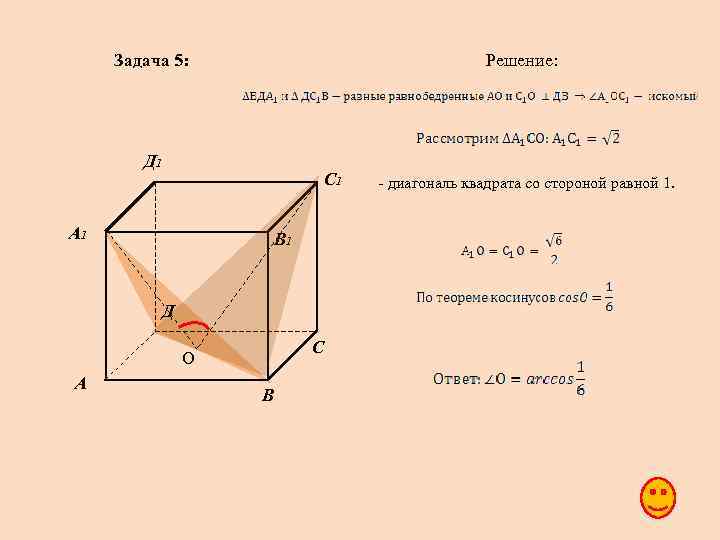Задача 5: Решение: Д 1 С 1 А 1 В 1 Д С О А В - диагональ квадрата со стороной равной 1.

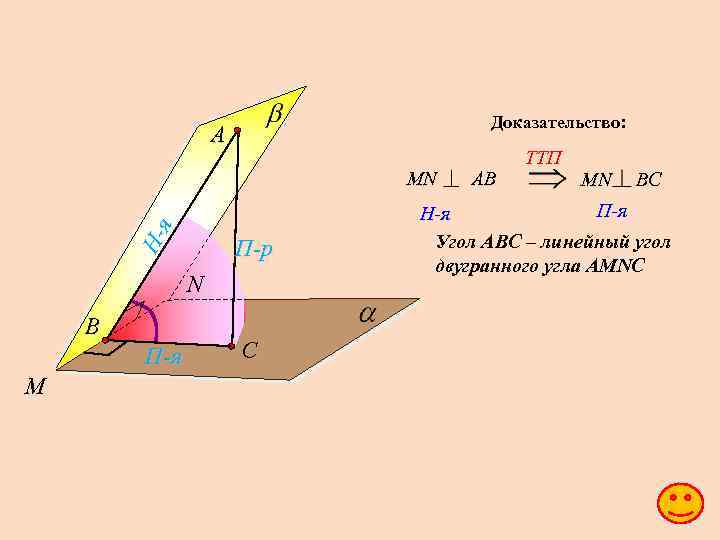Доказательство: А Ня МN П-р N В П-я M С АB TTП MN ВС П-я H-я Угол АВС – линейный угол двугранного угла АМNC

Урок окончен, удачи …