ПОСТРОЕНИЕ ГРАФИКОВ В ПРОГРАММЕ EXCEL АВТОР ЦОГОЕВ К

ПОСТРОЕНИЕ ГРАФИКОВ В ПРОГРАММЕ EXCEL АВТОР: ЦОГОЕВ К. Т. 2008 ГОД

Microsoft Excel ― это программа, которая позволяет не только работать с табличными данными, но и строить разнообразные графики.

УРОК 1. ГРАФИКИ ВИДА Y=F(X)

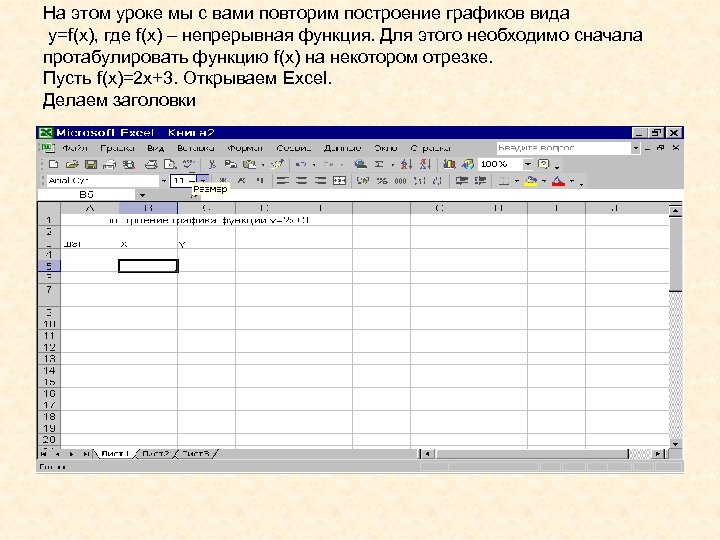На этом уроке мы с вами повторим построение графиков вида y=f(x), где f(x) – непрерывная функция. Для этого необходимо сначала протабулировать функцию f(x) на некотором отрезке. Пусть f(x)=2 x+3. Открываем Excel. Делаем заголовки

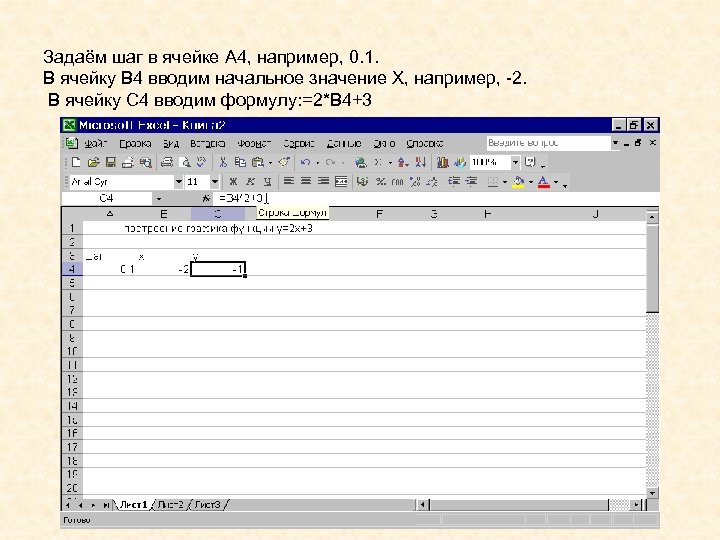Задаём шаг в ячейке A 4, например, 0. 1. В ячейку B 4 вводим начальное значение X, например, -2. В ячейку C 4 вводим формулу: =2*B 4+3

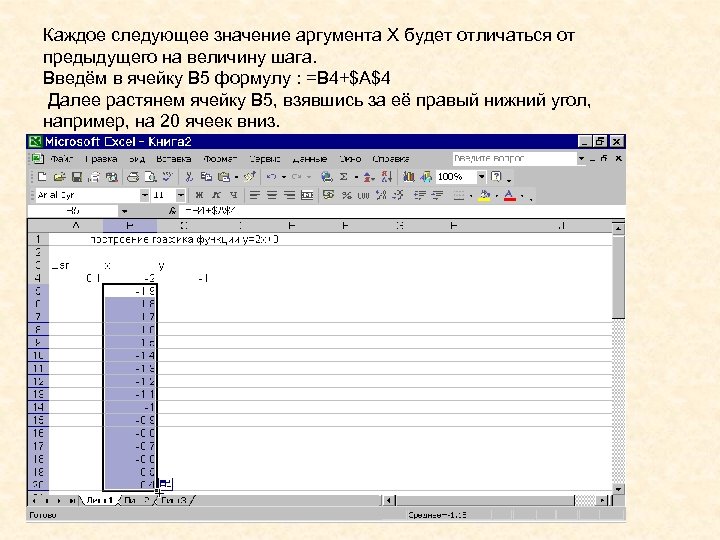Каждое следующее значение аргумента X будет отличаться от предыдущего на величину шага. Введём в ячейку B 5 формулу : =B 4+$A$4 Далее растянем ячейку B 5, взявшись за её правый нижний угол, например, на 20 ячеек вниз.

Обратите особое внимание на формулу =B 4+$A$4. Здесь к ячейке A 4 (величина шага) применяется абсолютная адресация. Это означает, что при копировании содержимого ячеек в формулах ссылка на данную ячейку сохранится. Вопрос: какая формула будет в ячейке B 7? =B 6+$A$4 То есть, меняется только адрес ячейки из столбца B.

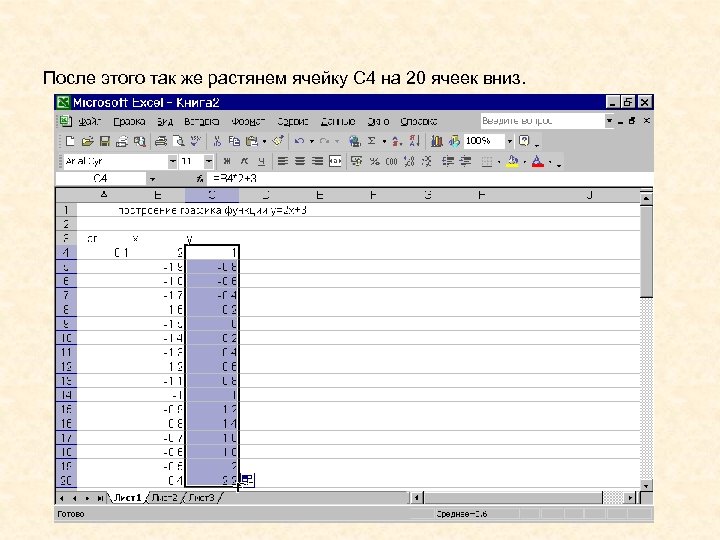После этого так же растянем ячейку С 4 на 20 ячеек вниз.

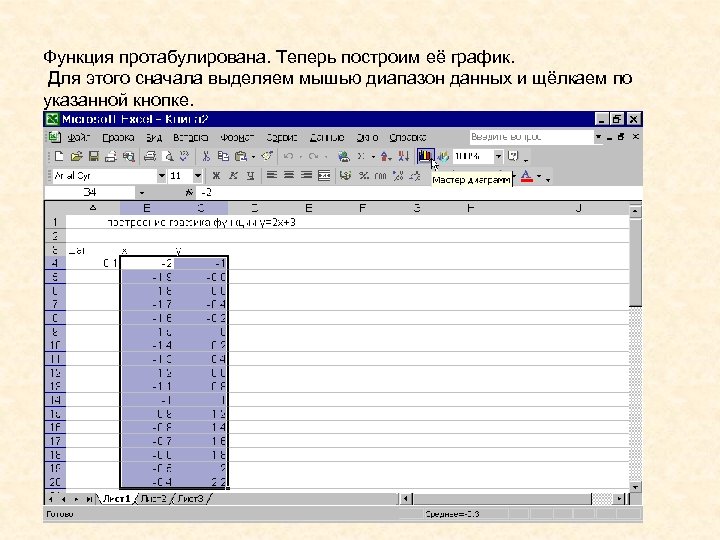Функция протабулирована. Теперь построим её график. Для этого сначала выделяем мышью диапазон данных и щёлкаем по указанной кнопке.

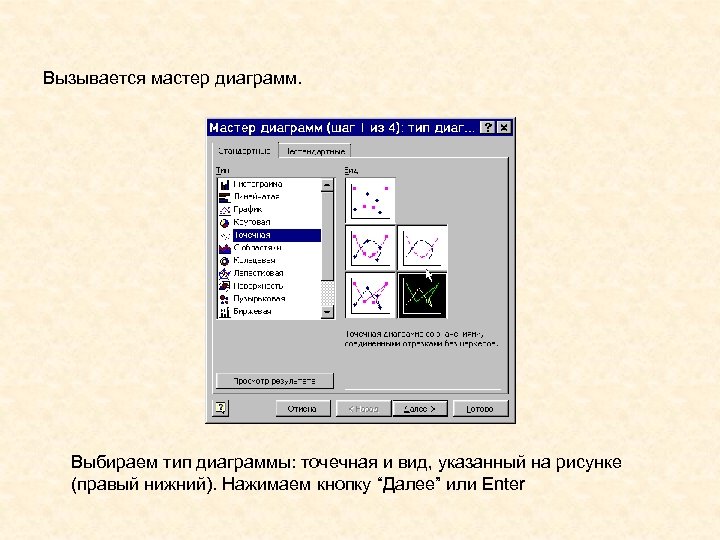Вызывается мастер диаграмм. Выбираем тип диаграммы: точечная и вид, указанный на рисунке (правый нижний). Нажимаем кнопку “Далее” или Enter

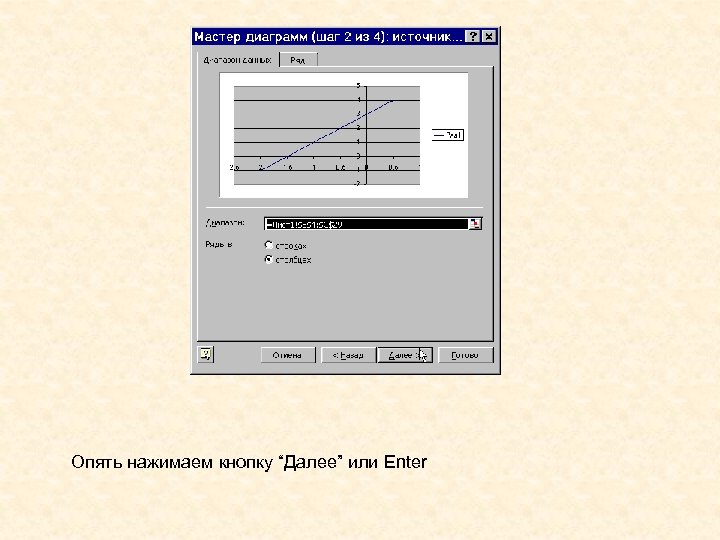Опять нажимаем кнопку “Далее” или Enter

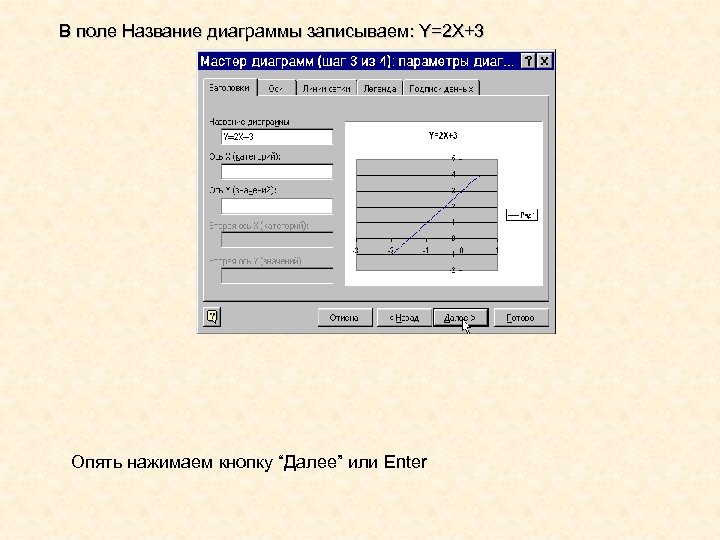В поле Название диаграммы записываем: Y=2 X+3 Опять нажимаем кнопку “Далее” или Enter

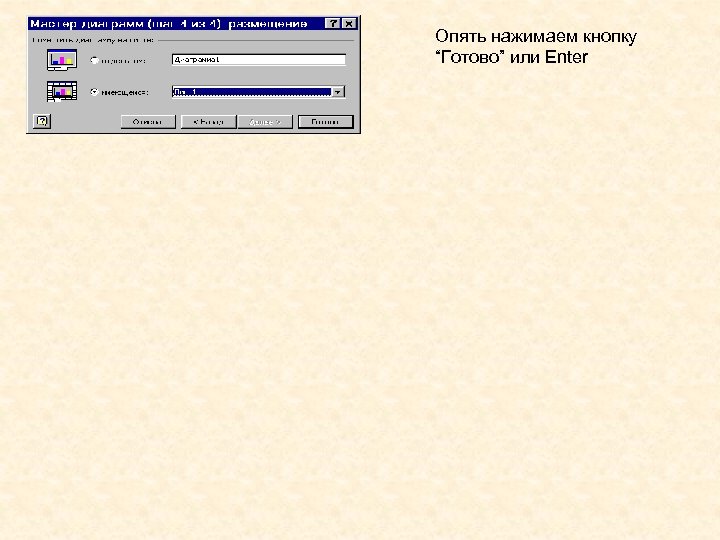Опять нажимаем кнопку “Готово” или Enter

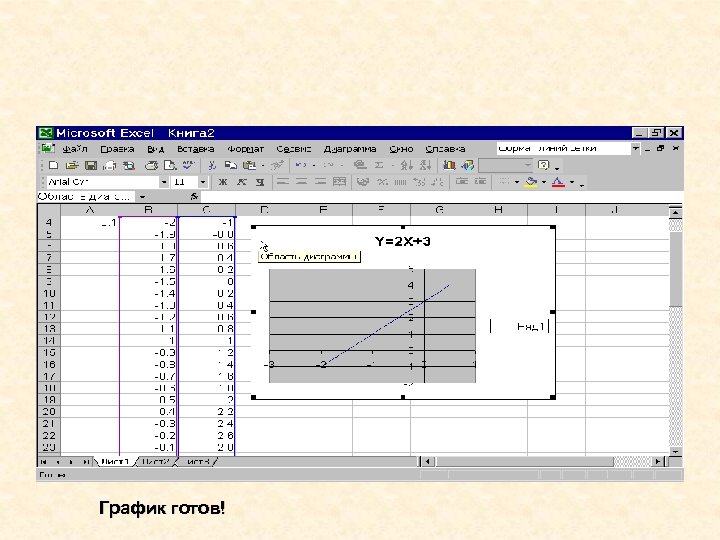График готов!

На этом уроке мы узнали: Что такое абсолютная адресация ячейки. Вспомнили, что формула в ячейке начинается со знака = как табулировать, то есть получить ряд значений функции. Как использовать Мастер диаграмм Домашнее задание

УРОК 2. ПОСТРОЕНИЕ КРИВЫХ, ЗАДАННЫХ ПАРАМЕТРИЧЕСКИ

Кривая, заданная параметрически, - это множество точек плоскости вида (X(T); Y(T)), где T – это независимая переменная, называемая в данном случае параметром. Таких кривых очень много. Мы познакомимся с некоторыми из них. 1. Архимедова спираль – это кривая, задаваемая так: 2. X(T)=T*COS(T), Y(T)=T*SIN(T) 3. T – задается в радианах и изменяется от 0 до бесконечности Давайте построим эту кривую. Запустим Excel. В данном случае нам нужно табулировать не одну, а две функции – X(T) и Y(T)

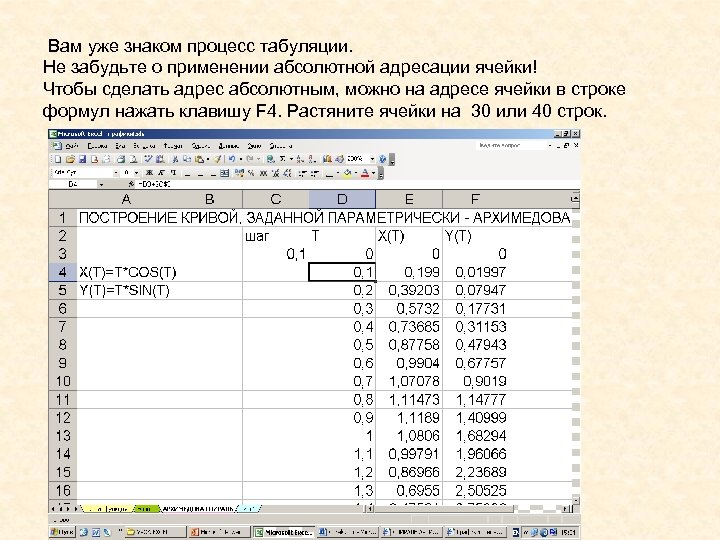Вам уже знаком процесс табуляции. Не забудьте о применении абсолютной адресации ячейки! Чтобы сделать адрес абсолютным, можно на адресе ячейки в строке формул нажать клавишу F 4. Растяните ячейки на 30 или 40 строк.

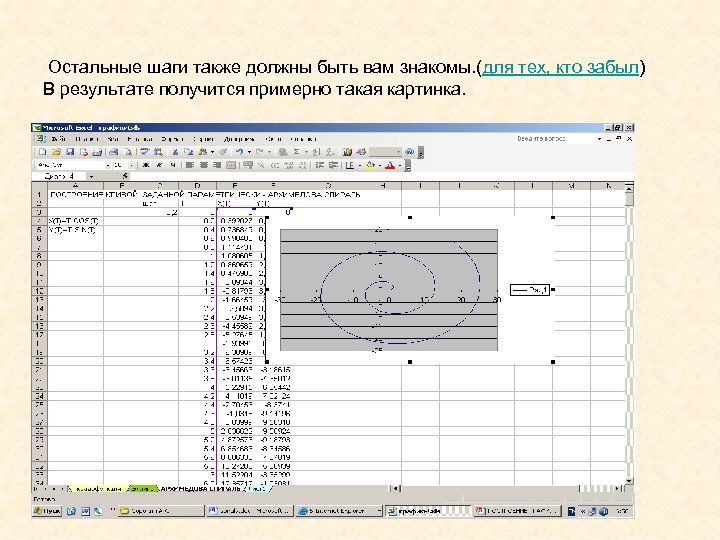Остальные шаги также должны быть вам знакомы. (для тех, кто забыл) В результате получится примерно такая картинка.

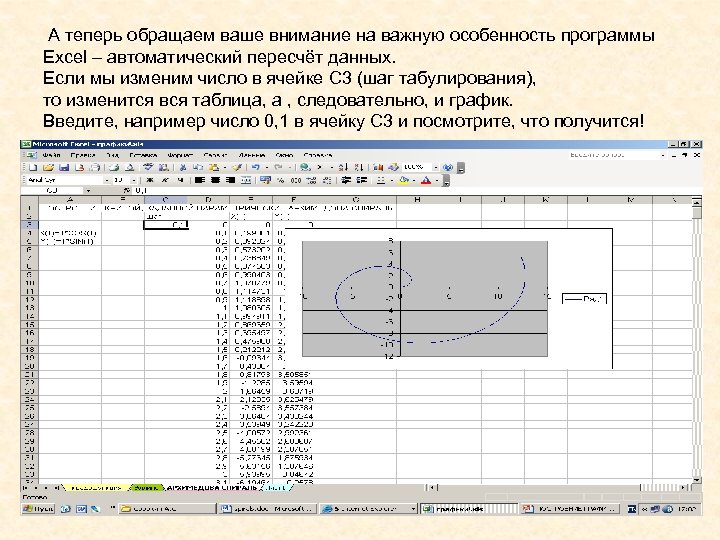А теперь обращаем ваше внимание на важную особенность программы Excel – автоматический пересчёт данных. Если мы изменим число в ячейке C 3 (шаг табулирования), то изменится вся таблица, а , следовательно, и график. Введите, например число 0, 1 в ячейку C 3 и посмотрите, что получится!

Построение окружности, заданной параметрически. . Давайте вспомним уравнение окружности в прямоугольных декартовых координатах. 2+Y 2=R 2 X Известно, что окружность задаётся параметрически так: X(T)=R*COS(T); Y(T)=R*SIN(T) Здесь T задаётся в радианах. R—радиус окружности. R – постоянная величина! Можете ли вы это доказать? Если нет, смотрите здесь

X(T)=R*COS(T) ; X 2(T)=R 2*COS 2(T) Y(T)=R*SIN(T) ; Y 2(T)=R 2*SIN 2(T) X 2(T)+ Y 2(T)= R 2*COS 2(T) + R 2*SIN 2(T)= R 2 ИЛИ X 2 + Y 2 = R 2

. Вопрос к классу. Прежде, чем табулировать функции X(T) и Y(T), нужно выяснить, в каких пределах изменяется параметр T? 0<=T<=2π или 0<=T<=6. 29 Учитывая это, постройте окружность самостоятельно

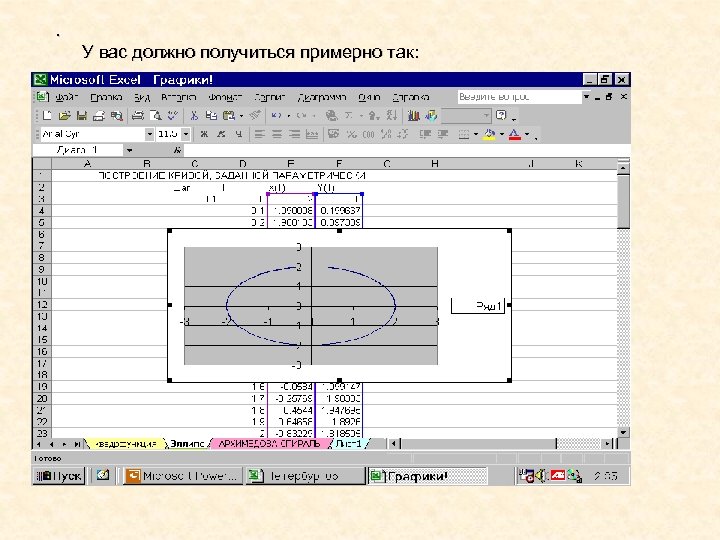. У вас должно получиться примерно так:

. Домашнее задание 1. Постройте окружность x 2+y 2=16 2. Постройте окружность x 2+y 2=R 2, где R выбирается пользователем