Построение графика квадратичной функции У У

Построение графика квадратичной функции»

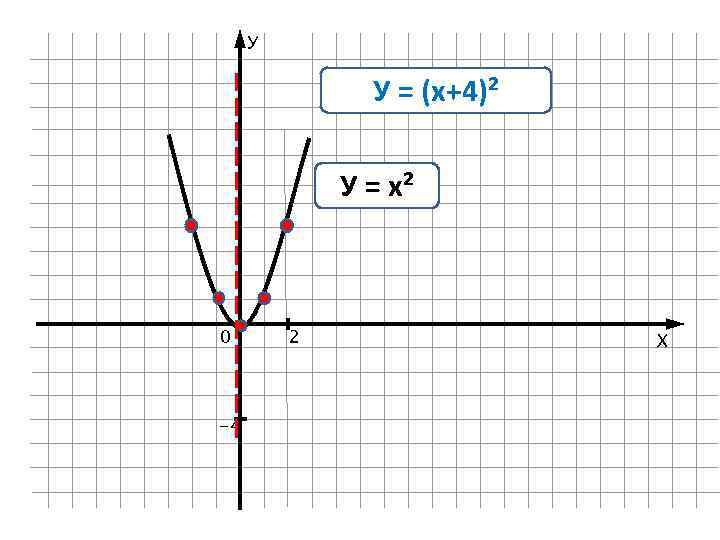У У = (х+4)² У = х² 0 -4 2 Х

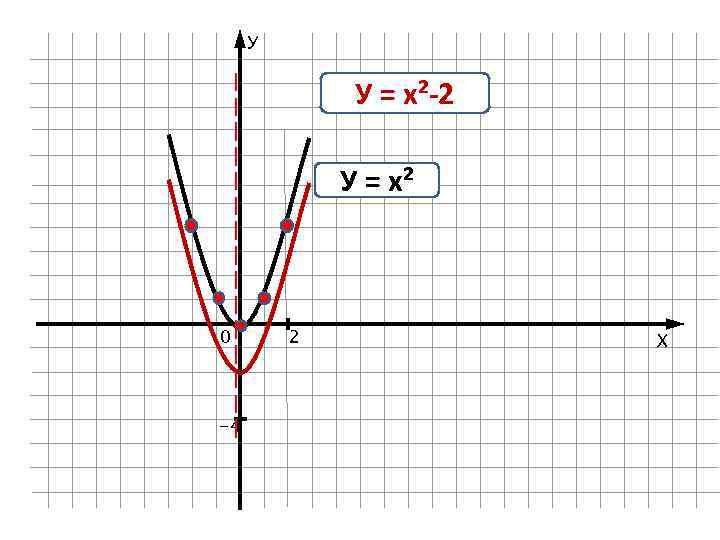У У = х²-2 У = х² 0 -4 2 Х

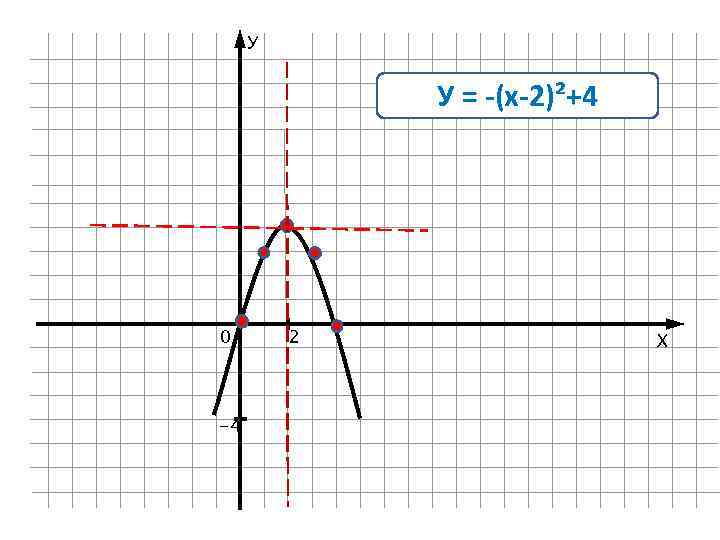У У = -(х-2)²+4 0 -4 2 Х

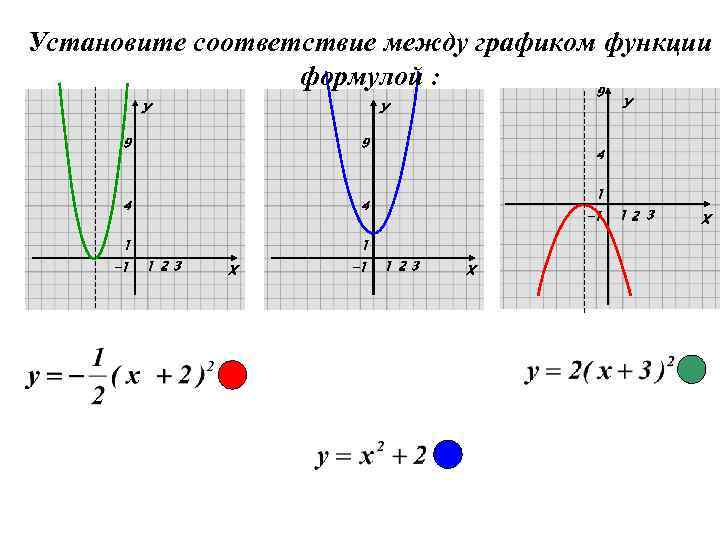Установите соответствие между графиком функции формулой : 9 У У У 9 9 4 4 1 1 -1 1 23 Х -1 4 1 -1 1 23 Х 12 3 Х

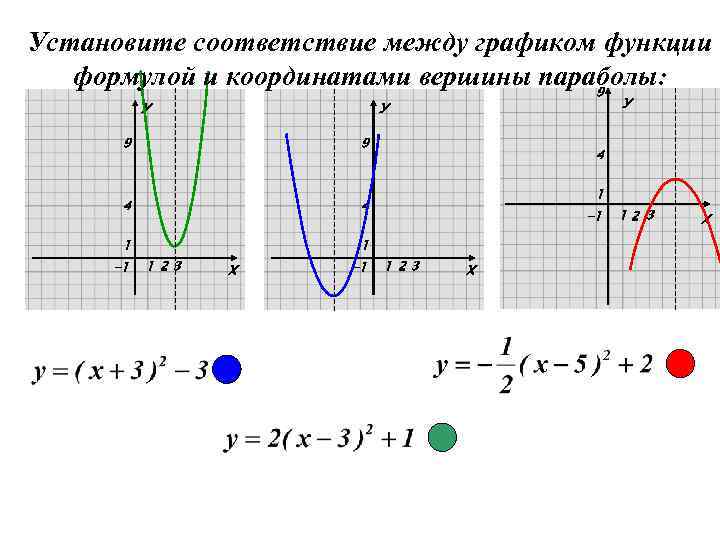Установите соответствие между графиком функции формулой и координатами вершины параболы: 9 У У У 9 9 4 4 1 1 -1 1 23 Х -1 4 1 -1 1 23 Х 12 3 Х

Квадратичной функцией называется функция, которую y=ax²+bx+c, можно задать формулой вида где х - независимая переменная, a, b и с -некоторые числа (причём а≠ 0). Например: у = 5 х²+6 х+3, у = -7 х²+8 х-2, у = 0, 8 х²+5, - квадратичные функции

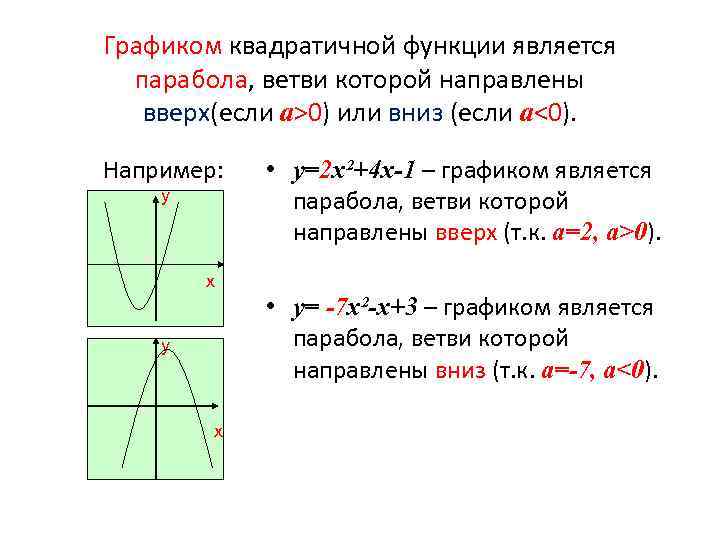Графиком квадратичной функции является парабола, ветви которой направлены вверх(если а>0) или вниз (если а<0). Например: у • у=2 х²+4 х-1 – графиком является парабола, ветви которой направлены вверх (т. к. а=2, а>0). 0 х у 0 х • у= -7 х²-х+3 – графиком является парабола, ветви которой направлены вниз (т. к. а=-7, а<0).

Чтобы построить график функции надо: 1. Описать функцию: название функции, что является графиком функции, куда направлены ветви параболы. Пример: у = х²-2 х-3 – квадратичная функция, графиком является парабола, ветви которой направлены вверх (т. к. а=1, а>0)

2. Найти координаты вершины Пример: у = х²-2 х-3 параболы А(х0; y 0) по (а = 1; b = -2; с = -3) формулам: Найдём координаты вершины параболы Прямая x=x 0 является осью симметрии параболы. А(1; -4) – вершина параболы. х=1 – ось симметрии параболы.

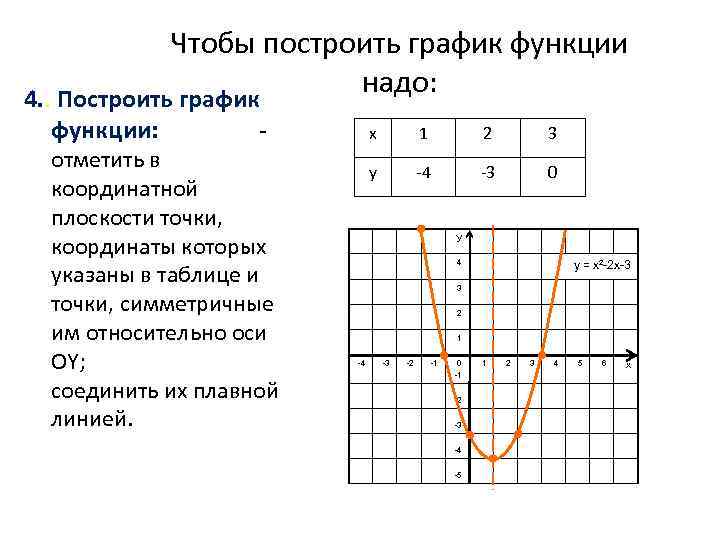Чтобы построить график функции надо: 4. . Построить график функции: - отметить в координатной плоскости точки, координаты которых указаны в таблице и точки, симметричные им относительно оси OY; соединить их плавной линией. х 1 2 3 у -4 -3 0 У 4 у = х²-2 х-3 3 2 1 -4 -3 -2 -1 0 -1 -2 -3 -4 -5 1 2 3 4 5 6 х

Построить в тетради график функции у = -2 х²+8 х-3

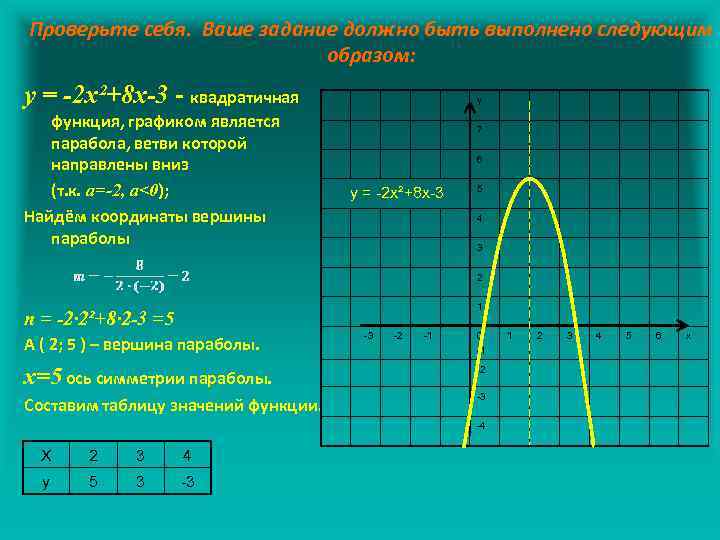Проверьте себя. Ваше задание должно быть выполнено следующим образом: у = -2 х²+8 х-3 - квадратичная функция, графиком является парабола, ветви которой направлены вниз (т. к. а=-2, а<0); Найдём координаты вершины параболы у 7 6 у = -2 х²+8 х-3 5 4 3 2 1 n = -2· 2²+8· 2 -3 =5 А ( 2; 5 ) – вершина параболы. -3 -2 -1 0 -1 х=5 ось симметрии параболы. -2 Составим таблицу значений функции. -3 -4 Х 2 3 4 у 5 3 -3 1 2 3 4 5 6 х

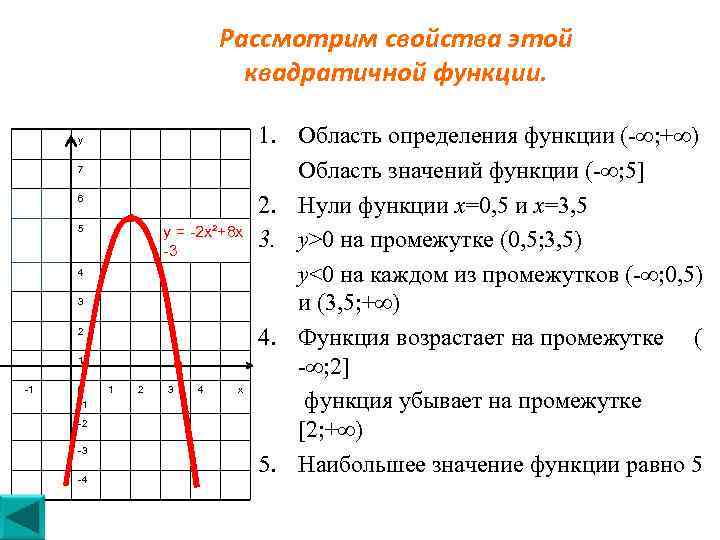Рассмотрим свойства этой квадратичной функции. у 7 6 у = -2 х²+8 х -3 5 4 3 2 1 -1 0 -1 -2 -3 -4 1 2 3 4 х 1. Область определения функции (-∞; +∞) Область значений функции (-∞; 5] 2. Нули функции х=0, 5 и х=3, 5 3. у>0 на промежутке (0, 5; 3, 5) y<0 на каждом из промежутков (-∞; 0, 5) и (3, 5; +∞) 4. Функция возрастает на промежутке ( -∞; 2] функция убывает на промежутке [2; +∞) 5. Наибольшее значение функции равно 5