ПОСТРОЕНИЕ ГРАФИКА КВАДРАТИЧНОЙ ФУНКЦИИ Повторим

ПОСТРОЕНИЕ ГРАФИКА КВАДРАТИЧНОЙ ФУНКЦИИ

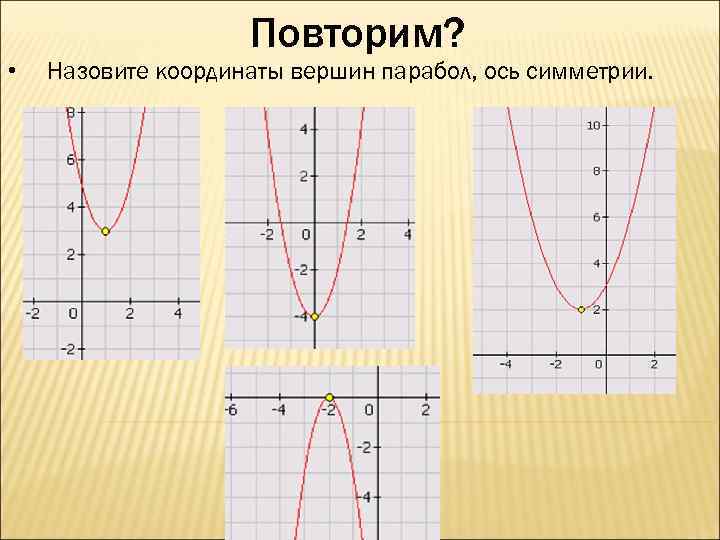• Повторим? Назовите координаты вершин парабол, ось симметрии.

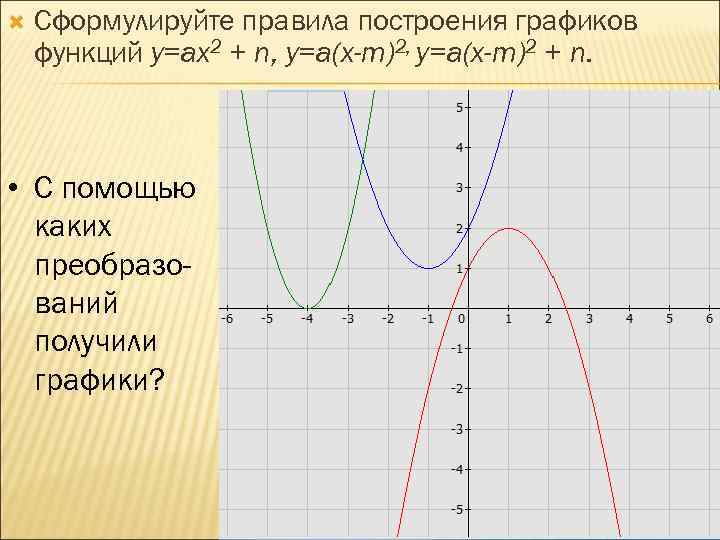Сформулируйте правила построения графиков функций у=ах2 + n, у=а(х-m)2 + n. • С помощью каких преобразований получили графики?

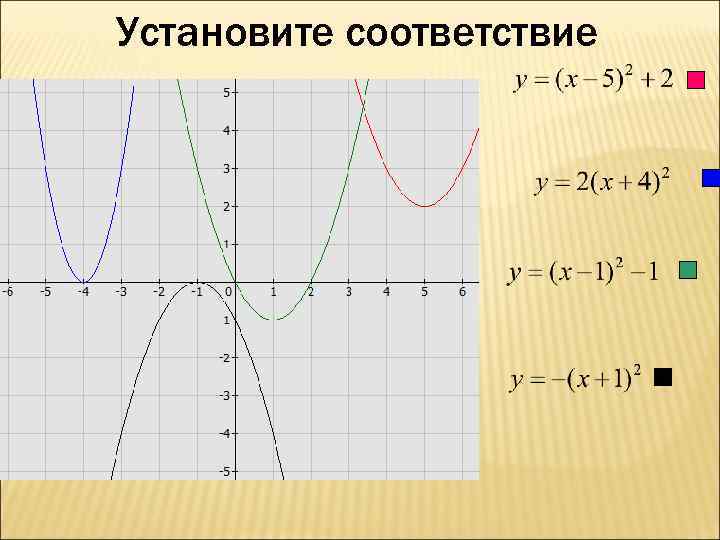Установите соответствие

ПАДЕНИЕ БАСКЕТБОЛЬНОГО МЯЧА

ПАРАБОЛИЧЕСКИЙ ФОНТАН

БИБЛИОТЕКА С КРЫШЕЙ В ФОРМЕ ПАРАБОЛЫ В НОРВЕГИИ

ЛУЧИ ПРОЖЕКТОРА

ВРАЩАЮЩИЙСЯ СОСУД С ЖИДКОСТЬЮ

ТЕМА УРОКА: Построение графика квадратичной функции ЦЕЛИ УРОКА: Сформулировать алгоритм построения графика квадратичной функции, т. е. функции вида y = ax 2+bx+c. Научиться строить график квадратичной функции по алгоритму.

АЛГОРИТМ ПОСТРОЕНИЯ ГРАФИКА КВАДРАТИЧНОЙ ФУНКЦИИ y = ax 2+bx+c Определить направление ветвей параболы Определить координаты вершины параболы (хо; у о) и отметить ее в координатной плоскости: хо = -b/2 a; у о= y(хо) Построить несколько точек, принадлежащих параболе Соединить отмеченные точки

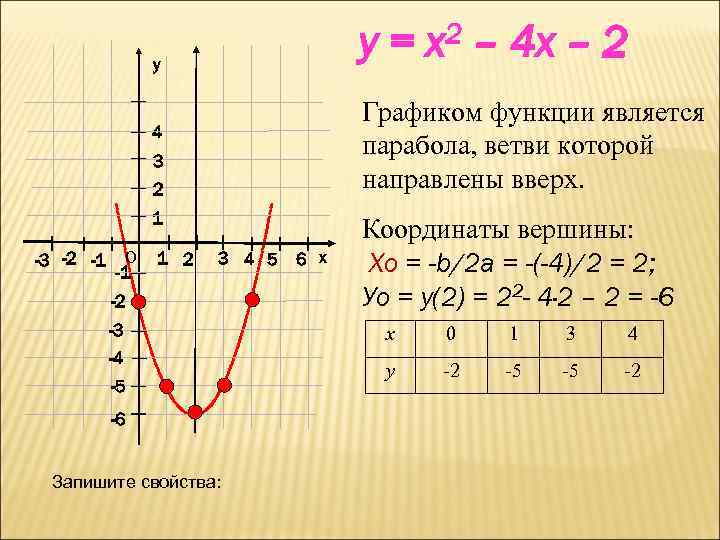y= y 3 2 1 0 -1 1 2 – 4 x – 2 Графиком функции является парабола, ветви которой направлены вверх. 4 -3 -2 -1 2 x 3 4 5 6 x -2 -3 -4 -5 -6 Запишите свойства: Координаты вершины: Хо = -b/2 a = -(-4)/2 = 2; Уо = y(2) = 22 - 4∙ 2 – 2 = -6 х 0 1 3 4 у -2 -5 -5 -2

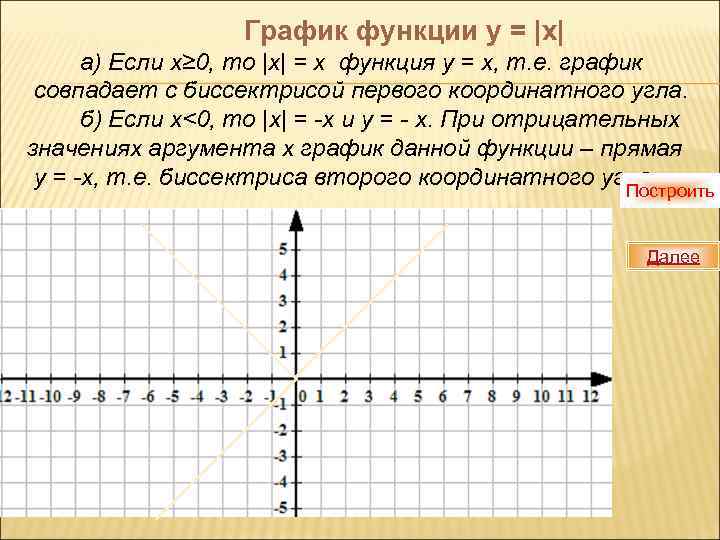График функции у = |х| а) Если х≥ 0, то |х| = х функция у = х, т. е. график совпадает с биссектрисой первого координатного угла. б) Если х<0, то |х| = -х и у = - х. При отрицательных значениях аргумента х график данной функции – прямая у = -х, т. е. биссектриса второго координатного угла. Построить Далее

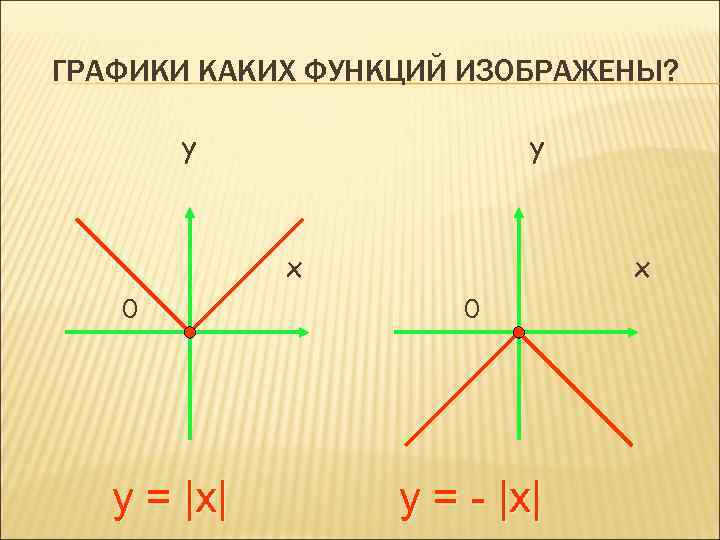ГРАФИКИ КАКИХ ФУНКЦИЙ ИЗОБРАЖЕНЫ? y y x 0 y = |x| x 0 y = - |x|

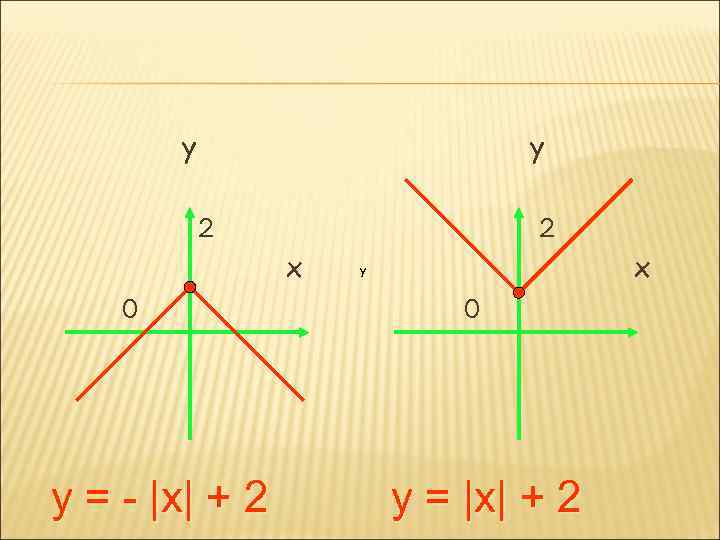y y 2 2 x 0 y = - |x| + 2 x y 0 y = |x| + 2

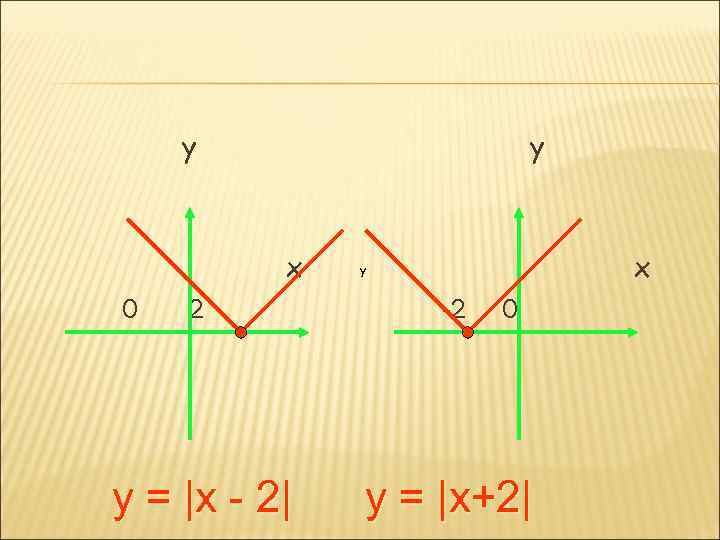y y x 0 x y 2 -2 0 y = |x - 2| y = |x+2|

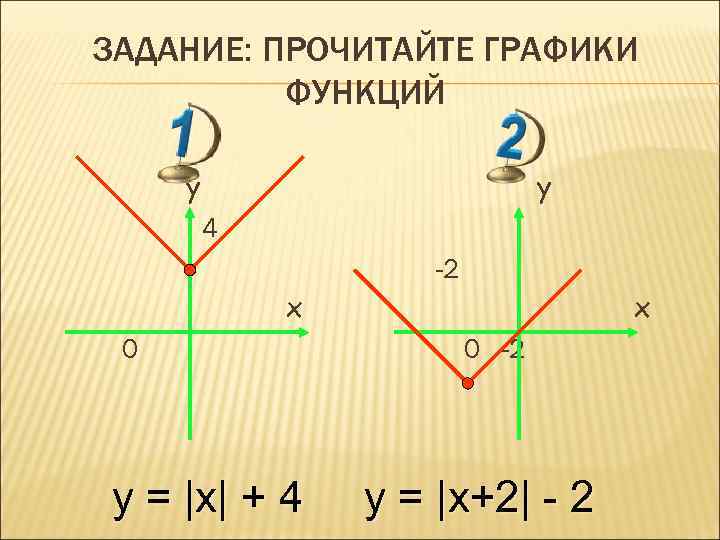ЗАДАНИЕ: ПРОЧИТАЙТЕ ГРАФИКИ ФУНКЦИЙ y y 4 -2 x 0 y = |x| + 4 x 0 -2 y = |x+2| - 2

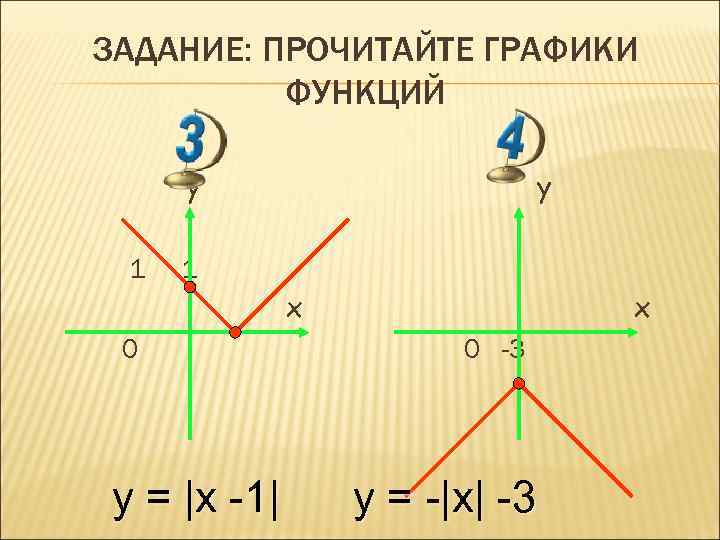ЗАДАНИЕ: ПРОЧИТАЙТЕ ГРАФИКИ ФУНКЦИЙ y 1 x 0 y = |x -1| x 0 -3 y = -|x| -3

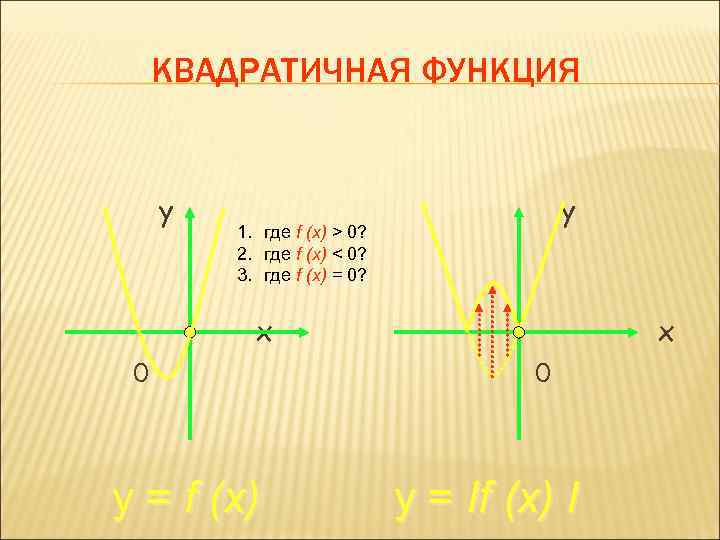КВАДРАТИЧНАЯ ФУНКЦИЯ y y 1. где f (x) > 0? 2. где f (x) < 0? 3. где f (x) = 0? x 0 y = f (x) x 0 y = If (x) I

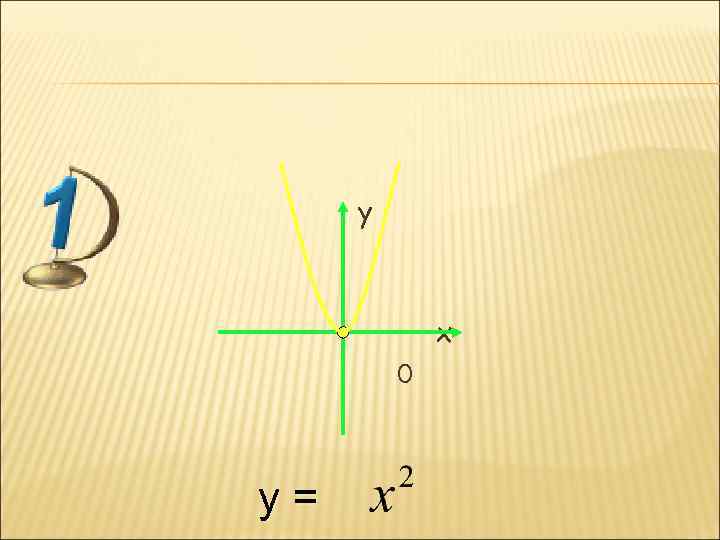y x 0 y=

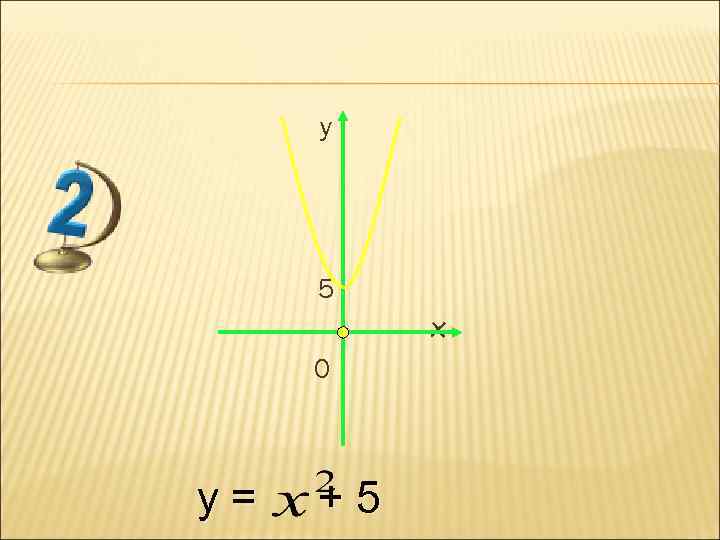y 5 x 0 y= +5

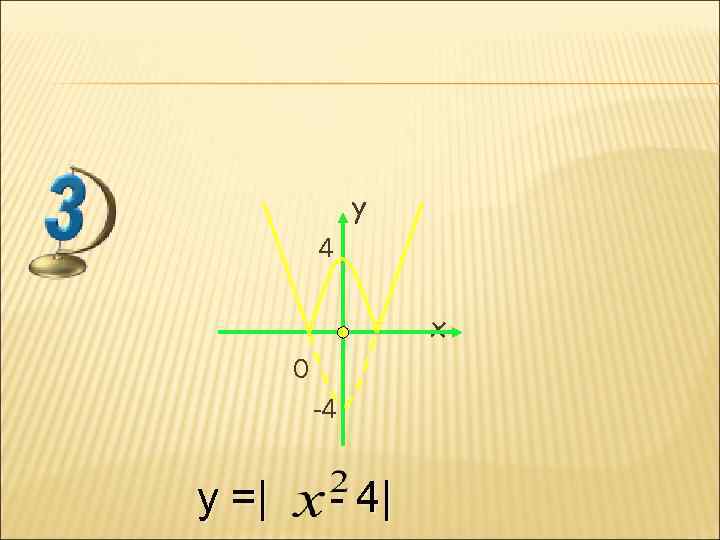y 4 x 0 -4 y =| - 4|

САМОСТОЯТЕЛЬНАЯ РАБОТА: 1 вариант Построить графики функций, записать свойства: 2 -2 у=х 1) 2) у=Iх-1 I+3 2 вариант Построить графики функций, записать свойства: 2+2 у=-х 1) 2) у=Iх+2 I-3

ДРЕВНЯЯ КИТАЙСКАЯ МУДРОСТЬ СКАЖИ МНЕ - И Я ЗАБУДУ, ПОКАЖИ МНЕ - И Я ЗАПОМНЮ, ВОВЛЕКИ МЕНЯ – И Я ПОЙМУ