Поразрядная сортировка Radix sort Рассматриваемый ниже алгоритм существенно отличается

Поразрядная сортировка(Radix sort) Рассматриваемый ниже алгоритм существенно отличается от описанных ранее. Во-первых, он совсем не использует сравнений сортируемых элементов. Во-вторых, ключ, по которому происходит сортировка, необходимо разделить на части, разряды ключа. Например, слово можно разделить по буквам, число - по цифрам. . . До сортировки необходимо знать два параметра: k и m, где • k - количество разрядов в самом длинном ключе • m - разрядность данных: количество возможных значений разряда ключа При сортировке русских слов m = 33, так как буква может принимать не более 33 значений. Если в самом длинном слове 10 букв, k = 10. Аналогично, для шестнадцатиричных чисел m=16, если в качестве разряда брать цифру, и m=256, если использовать побайтовое деление. Эти параметры нельзя изменять в процессе работы алгоритма. В этом - еще одно отличие метода от вышеописанных.

Поразрядная сортировка для списков Предположим, что элементы линейного списка L есть k-разрядные десятичные числа, разрядность максимального числа известна заранее. Обозначим d(j, n) - j-ю справа цифра числа n, которую можно выразить как d(j, n) = [ n / 10 j-1 ] % 10 Пусть L 0, L 1, . . . , L 9 - вспомогательные списки (карманы), вначале пустые. Поразрядная сортировка состоит из двух процессов, называемых распределение и сборка и выполняемых для j=1, 2, . . . , k. Фаза распределения разносит элементы L по карманам: элементы li списка L последовательно добавляются в списки Lm, где m = d(j, li). Таким образом получаем десять списков, в каждом из которых j-тые разряды чисел одинаковы и равны m. Фаза сборки состоит в объединении списков L 0, L 1, . . . , L 9 в общий список L = L 0 => L 1 => L 2 =>. . . => L 9

Поразрядная сортировка для списков (2) Рассмотрим пример работы алгоритма на входном списке 0 => 8 => 12 => 56 => 7 => 26 => 44 => 97 => 2 => 37 => 4 => 3 => 45 => 10. Максимальное число содержит две цифры, значит, разрядность данных k=2. Первый проход, j=1. Распределение по первой справа цифре: L 0: 0 => 10 // все числа с первой справа цифрой 0 L 1: пусто L 2: 12 => 2 L 3: 3 => 3 L 4: 44 => 4 L 5: 45 L 6: 56 => 26 L 7: 7 => 97 => 37 L 8: 8 L 9: пусто // все числа с первой справа цифрой 9 Cборка: соединяем списки Li один за другим L: 0 => 12 => 3 => 44 => 45 => 56 => 26 => 7 => 97 => 37 => 8

Поразрядная сортировка для списков (3) Второй проход, j=2. Распределение по второй справа цифре: L 0: 0 => 2 => 3 => 4 => 7 => 8 L 1: 10 => 12 L 2: 26 L 3: 37 L 4: 44 => 45 L 5: 56 L 6: пусто L 7: пусто L 8: пусто L 9: 97 Cборка: соединяем списки Li один за другим L: 0 => 2 => 3 => 4 => 7 => 8 => 10 => 12 => 26 => 37 => 44 => 45 => 56 => 97

Поразрядная сортировка для списков (4) Число используемых карманов - количество возможных значений элемента списка. Сортировку можно организовать так, чтобы не использовать дополнительной памяти для карманов, т. е элементы списка не перемещать, а с помощью перестановки указателей присоединять их к тому или иному карману. В представленной ниже программе функция radix_list реализует поразрядную сортировку связанного линейного списка (указатель l), в котором содержатся t-разрядные десятичные положительные числа, без использования дополнительной памяти. Параметры head[i], tail[i] указывают соответственно на первый и на последний элементы кармана Li. При этом сами карманы являются "виртуальными", память под них не выделяется.

Поразрядная сортировка для списков (5) typedef struct slist_ { long val; struct slist_ *next; } slist; // функция сортировки возвращает указатель на начало отсортированного списка slist *radix_list(slist *l, int t) { // t - разрядность (максимальная длина числа) int i, j, d, m=1; slist *temp, *out, *head[10], *tail[10]; out=l; for (j=1; j<=t; j++) { for (i=0; i<=9; i++) head[i] = (tail[i]=NULL); while ( l != NULL ) { d = ((int)(l->val/m))%(int)10; temp = tail[d]; if ( head[d]==NULL ) head[d] = l; else temp->next = l; temp = tail[d] = l; l = l->next; temp->next = NULL; } for (i=0; i<=9; i++) if ( head[i] != NULL ) break; l = head[i]; temp = tail[i]; for (d=i+1; d<=9; d++) { if ( head[d] != NULL) { temp->next = head[d]; temp = tail[d]; } } m*=10; } return (out); }

Поразрядная сортировка для массивов Списки довольно удобны тем, что их легко реорганизовывать, объединять и т. п. Как применить ту же идею для массивов ? СОРТИРОВКА ПОДСЧЕТОМ Пусть у нас есть массив source из n десятичных цифр ( m = 10 ). Например, source[7] = { 7, 9, 8, 5, 4, 7, 7 }, n=7. Здесь положим const k=1. 1. Создать массив count из m элементов(счетчиков). 2. Присвоить count[i] количество элементов source, равных i. Для этого: a) проинициализовать count[] нулями, b) пройти по source от начала до конца, для каждого числа увеличивая элемент count с соответствующим номером. for( i=0; i

Поразрядная сортировка для массивов (2) Для каждого числа source[i] мы знаем, сколько чисел меньше него - это значение хранится в count[ source[i] ]. Таким образом, нам известно окончательное место числа в упорядоченном массиве: если есть K чисел меньше данного, то оно должно стоять на позиции K+1. Осуществляем проход по массиву source слева направо, одновременно заполняя выходной массив dest: for ( i=0; i

Поразрядная сортировка для массивов (3) Итак, мы научились за (n + m) сортировать цифры. А от цифр до строк и чисел - 1 шаг. Пусть у нас в каждом ключе k цифр ( m = 10 ). Аналогично случаю со списками отсортируем их в несколько проходов от младшего разряда к старшему. Общее количество операций, таким образом, ( k(n+m) ), при используемой дополнительно памяти (n+m). Эта схема допускает небольшую оптимизацию. Заметим, что сортировка по каждому байту состоит из 2 проходов по всему массиву: на первом шаге и на четвертом. Однако, можно создать сразу все массивы count[] (по одному на каждую позицию) за один проход. Неважно, как расположены числа - счетчики не меняются, поэтому это изменение корректно. Таким образом, первый шаг будет выполняться один раз за всю сортировку, а значит, общее количество проходов изменится с 2 k на k+1.

Поразрядная сортировка беззнаковых целых чисел В качестве интересного примера рассмотрим компьютерное представление целых беззнаковых чисел. На хранение каждого из базовых типов выделяется строго определенное количество байт. Как правило, распределение такое: unsigned char - 1 байт, unsigned short int - 2 байта, unsigned long int - 4 байта. При этом большинство процессоров использует обратный порядок записи: от младшего байта к старшему. Так число типа short int i = 669110 = 0 x 1 A 23 непосредственно в памяти хранится так: Если это число имеет тип long int, то под него выделяется 4 байта: long int i = 669110 = 0 x 00001 A 23. В конце расположены ведущие нули. Таким образом, необходимо провести сортировку от начала числа к концу. Каждый байт может принимать в общем случае 256 значений: m=256.

Поразрядная сортировка беззнаковых целых чисел (2) // Создать счетчики. // data-сортируемый массив, counters-массив для счетчиков, Nчисло элементов в data template void create. Counters(T *data, long *counters, long N) { // i-й массив count расположен, начиная с адреса counters+256*i memset( counters, 0, 256*sizeof(T)*sizeof(long) ); uchar *bp = (uchar*)data; uchar *data. End = (uchar*)(data + N); ushort i; while ( bp != data. End ) { // увеличиваем количество байт со значением *bp // i - текущий массив счетчиков for (i=0; i

Поразрядная сортировка беззнаковых целых чисел (3) // // // Функция radix. Pass принимает в качестве параметров номер байта Offset, число элементов N, исходный массив source, массив dest, куда будут записываться числа, отсортированные по байту Offset массив счетчиков count, соответствующий текущему проходу. template void radix. Pass (short Offset, long N, T *source, T *dest, long *count) { // временные переменные T *sp; long s, c, i, *cp; uchar *bp; // шаг 3 s = 0; // временная переменная, хранящая сумму на данный момент cp = count; for (i = 256; i > 0; --i, ++cp) { c = *cp; *cp = s; s += c; } // шаг 4 bp = (uchar *)source + Offset; sp = source; for (i = N; i > 0; --i, bp += sizeof(T) , ++sp) { cp = count + *bp; dest[*cp] = *sp; ++(*cp); } }

Поразрядная сортировка беззнаковых целых чисел (4) Процедура сортировки заключается в осуществлении sizeof(T) проходов по направлению от младшего байта к старшему. // сортируется массив in из N элементов // T - любой беззнаковый целый тип template void radix. Sort (T* &in, long N) { T *out = new T[N]; long *counters = new long[sizeof(T)*256], *count; create. Counters(in, counters, N); for (ushort i=0; i

Поразрядная сортировка целых чисел со знаком Формат IEEE-754 Поразрядная сортировка целых чисел с плавающей точкой Эффективность поразрядной сортировки Результаты тестирования

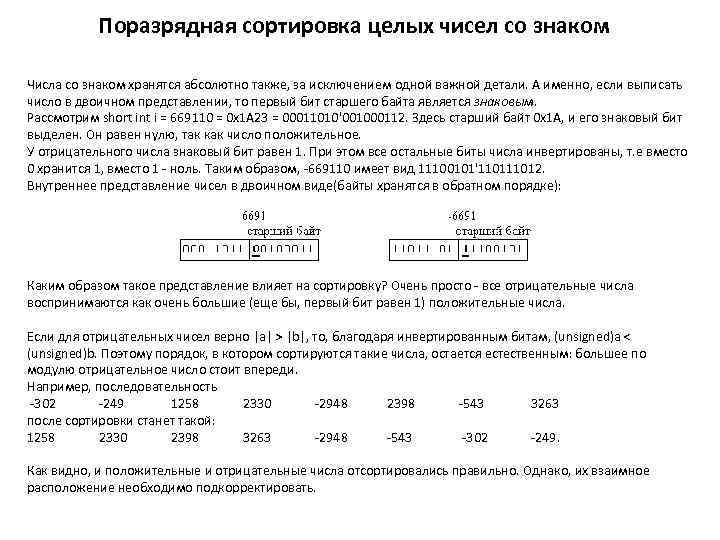Поразрядная сортировка целых чисел со знаком Числа со знаком хранятся абсолютно также, за исключением одной важной детали. А именно, если выписать число в двоичном представлении, то первый бит старшего байта является знаковым. Рассмотрим short int i = 669110 = 0 x 1 A 23 = 00011010'001000112. Здесь старший байт 0 x 1 A, и его знаковый бит выделен. Он равен нулю, так как число положительное. У отрицательного числа знаковый бит равен 1. При этом все остальные биты числа инвертированы, т. е вместо 0 хранится 1, вместо 1 - ноль. Таким образом, -669110 имеет вид 11100101'11012. Внутреннее представление чисел в двоичном виде(байты хранятся в обратном порядке): Каким образом такое представление влияет на сортировку? Очень просто - все отрицательные числа воспринимаются как очень большие (еще бы, первый бит равен 1) положительные числа. Если для отрицательных чисел верно |a| > |b|, то, благодаря инвертированным битам, (unsigned)a < (unsigned)b. Поэтому порядок, в котором сортируются такие числа, остается естественным: большее по модулю отрицательное число стоит впереди. Например, последовательность -302 -249 1258 2330 -2948 2398 -543 3263 после сортировки станет такой: 1258 2330 2398 3263 -2948 -543 -302 -249. Как видно, и положительные и отрицательные числа отсортировались правильно. Однако, их взаимное расположение необходимо подкорректировать.

Поразрядная сортировка целых чисел со знаком (2) Как видно, и положительные и отрицательные числа отсортировались правильно. Однако, их взаимное расположение необходимо подкорректировать. Для этого модифицируем последний проход сортировки, работающий со старшими байтами и производящий окончательную расстановку. Все, что нам необходимо - узнать номер первого отрицательного числа num. Neg, и заполнять массив dest сначала числами после num. Neg(отрицательными), а потом - остальными(положительными). Определить по старшему байту знак числа можно без битовых операций, по результатам сравнения. После шага 1 в count[i] содержится количество байт, равных i. Отрицательных чисел столько же, сколько байт с единичным старшим битом, т. е равных 128. . . 255: long num. Neg=0; // количество отрицательных чисел for(i=128; i<256; i++) num. Neg += count[i]; На шаге 3 увеличиваем начальную позицию положительных чисел на num. Neg, а отрицательные записываем с начала массива. Это приводит к следующей процедуре: // проход поразрядной сортировки по старшим байтам, // для целых чисел со знаком Offset = sizeof(T)-1. template void signed. Radix. Last. Pass (short Offset, long N, T *source, T *dest, long *count) { T *sp; long s, c, i, *cp; uchar *bp; // подсчет количества отрицательных чисел long num. Neg=0; for(i=128; i<256; i++) num. Neg += count[i];

Поразрядная сортировка целых чисел со знаком (3) // первые 128 элементов count относятся к положительным числам. // отсчитываем номер первого числа, начиная от num. Neg s = num. Neg; cp = count; for (i = 0; i < 128; ++i, ++cp) { c = *cp; *cp = s; s += c; } // номера для отрицательных чисел отсчитываем от начала массива s = 0; cp = count+128; for (i = 0; i < 128; ++i, ++cp) { c = *cp; *cp = s; s += c; } bp = (uchar *)source + Offset; sp = source; for (i = N; i > 0; --i, bp += sizeof(T) , ++sp) { cp = count + *bp; dest[*cp] = *sp; ++(*cp); } }

Поразрядная сортировка целых чисел со знаком (3) Соответственным образом изменится и внешняя процедура сортировки. На последнем шаге теперь происходит вызов signed. Radix. Last. Pass. template void signed. Radix. Sort (T* &in, long N) { T *out = new T[N]; ushort i; long *counters = new long[sizeof(T)*256], *count; create. Counters(in, counters, N); for (i=0; i

Формат IEEE-754 Особенно подходящим местом применения radix. Sort является компьютерная графика. Есть много координат, которые необходимо отсортировать, причем с наибольшей скоростью. Поэтому было бы очень удобно распространить возможности процедуры на числа с плавающей точкой. С другой стороны, существует несколько стандартов для представления таких чисел. Наиболее известным следует признать IEEE-754, который используется в IBM PC, Macintosh, Dreamcast и ряде других систем. Зафиксировав формат представления числа, уже можно модифицировать соответствующим образом сортировку. Любое число можно записать в системе с основанием BASE как M*BASEn, где |M|

Формат IEEE-754 (2) Рассмотрим числа одинарной точности(float). Как и в целых числах, значение знакового бита 0 означает, что число положительное, значение 1 - число отрицательное. Так как первая цифра мантиссы всегда равна 1, то хранится только ее дробная часть. То есть, если M=1. 010112, то [Мантисса]= 010112. Если M=1. 10112, то [Мантисса]=10112. Таким образом в 23 битах хранится мантисса до 24 бит длиной. Чтобы получить из поля [Мантисса] правильное значение M необходимо мысленно прибавить к его значению единицу с точкой. Для удобства представления отрицательного порядка в соответствующем поле реально хранится порядок+смещение. Например, если n=0, то [Порядок]=127. Если n=-7, то [Порядок]=120. Таким образом, его значение всегда неотрицательно. Таким образом, общая формула по получению обычной записи числа из формата IEEE -754: N = (-1)[Знак] * 1. [Мантисса] * 2[Порядок]-127 (нормализованная запись, 1) Для 10. 2510 = 1010. 012 = +1. 01001 * 23 соответствующие значения будут [Знак]=0 (+) , [Порядок] = 130(=3+127), [Мантисса] = 010012. При значениях [Порядок]=1. . . 254 эта система позволяет представлять числа приблизительно от +-3, 39*10 -38 до +-3, 39*10+38.

Формат IEEE-754 (3) Особым образом обрабатываются [Порядок]=0 и [Порядок]=255. Если [Порядок]=0, но мантисса отлична от нуля, то перед ее началом необходимо ставить вместо единицы ноль с точкой. Так что формула меняется на N = (-1)[Знак] * 0. [Мантисса] * 2 -126 (денормализованная запись, 2) Это расширяет интервал представления чисел до +-1, 18*10 -38. . +-3, 39*10+38 [Порядок]=0 [Мантисса]=0 обозначают ноль. Возможно существование двух нулей: +0 и -0, которые отличаются битом знака, но при операциях ведут себя одинаково. В этом смысле можно интерпретировать ноль как особое денормализованное число со специальным порядком. Значение [Порядок]=255(все единицы) зарезервировано для специальных целей, более подробно описанных в стандарте. Такое поле в зависимости от мантиссы обозначает одно из трех специальных "нечисел", которые обозначают как Inf, Na. N, Ind, и может появиться в результате ошибок в вычислениях и при переполнении. Числа двойной точности устроены полностью аналогичным образом, к порядку прибавляется не 127, а 1023. Увеличение длин соответствующих полей позволяет хранить числа от 10 -323. 3 до 10308. 3, значение [Порядок]=2047(все единицы) зарезервировано под "нечисла".

Поразрядная сортировка целых чисел с плавающей точкой У рассмотренного представления есть одна интересная особенность. А именно, если значение поля [Порядок] у одного числа больше соответствующего значения у другого, то первое число обязательно больше второго. Это следует непосредственно из формул перевода (1) и (2) и верно для неотрицательных чисел. Если порядки равны, то сравниваются мантиссы. Это полностью соответствует обычной системе для целых чисел, когда сравниваются сначала старшие двоичные цифры, затем младшие. Таким образом, можно интерпретировать числа стандарта IEEE-754 как целые соответствующей длины: a > b равносильно (ulong)a > (ulong)b, если a, b > 0. Неприятности начинаются с отрицательными числами. Первый бит равен единице, так что это число будет, как и в случае беззнаковых целых, очень большим положительным. Больше любого по-настоящему положительного. Если a>0, b<0, то всегда (ulong)a < (ulong)b С другой стороны, никакого инвертирования битов, как в случае целых чисел со знаком, не производится. Поэтому большее по модулю отрицательное число дает большее в беззнаковой целочисленной интерпретации. a > b равносильно (ulong)a < (ulong)b, если a, b < 0.

Поразрядная сортировка целых чисел с плавающей точкой (2) Если запустить Radix. Sort на массиве: -302 -249 1258 2330 -2948 -543 2398 3263 после сортировки получим: 1258 2330 2398 3263 -249 -302 -543 -2948. Сначала идут положительные числа, которые отсортировались абсолютно правильно. Затем идут отрицательные, но в обратном порядке! Все, что необходимо сделать - это передвинуть их на правильное место тем же способом, что и при сортировке целых со знаком, при этом обратив порядок их расположения. Эти изменения можно провести на шаге 3 последнего прохода, работающего со старшими байтами. Отрицательные числа расположены в обратном порядке, поэтому при вычислении их расположения необходимо идти от count[255]=0, соответствующего наименьшему отрицательному числу до count[128]. При этом в массив нужно записывать сумму всех чисел после текущего, включая само текущее. s = count[255] = 0; // отрицательные числа располагаются от нуля cp = count+254; for (i = 254; i >= 128; --i, --cp) { *cp += s; s = *cp; }

Поразрядная сортировка целых чисел с плавающей точкой (3) Теперь можно написать окончательную реализацию. // Функция для последнего прохода при поразрядной сортировке чисел с // плавающей точкой template void float. Radix. Last. Pass (short Offset, long N, T *source, T *dest, long *count) { T *sp; long s, c, i, *cp; uchar *bp; long num. Neg=0; for(i=128; i<256; i++) num. Neg += count[i]; s=num. Neg; cp = count; for (i = 0; i < 128; ++i, ++cp) { c = *cp; *cp = s; s += c; }

Поразрядная сортировка целых чисел с плавающей точкой (4) // изменения, касающиеся обратного расположения // отрицательных чисел. s = count[255] = 0; // cp = count+254; // for (i = 254; i >= 128; --i, --cp) {// *cp += s; // остальное - то же, что и в s = *cp; // signed. Radix. Last. Pass } bp = (uchar *)source + Offset; sp = source; for (i = N; i > 0; --i, bp += sizeof(T) , ++sp) { cp = count + *bp; if (*bp<128) dest[ (*cp)++ ] = *sp; else dest[ --(*cp) ] = *sp; } }

Поразрядная сортировка целых чисел с плавающей точкой (5) // поразрядная сортировка чисел с плавающей точкой template void float. Radix. Sort (T* &in, long N) { T *out = new T[N]; ushort i; long *counters = new long[sizeof(T)*256], *count; create. Counters(in, counters, N); for (i=0; i

Эффективность поразрядной сортировки Рост быстрой сортировки мы уже знаем: O(nlogn). Судя по оценке, поразрядная сортировка растет линейным образом по n, так как k, m - константы. Также она растет линейным образом по k - при увеличении длины типа(количества разрядов) соответственно возрастает число проходов. Однако, в последний пункт реальные условия вносят свои коррективы. Дело в том, что основной цикл сортировки по i-му байту состоит в движении указателя uchar* bp шагами sizeof(T) по массиву для получения очередного разряда. Когда T=char, шаг равен 1, T=short - шаг равен 2, T=long - шаг равен 4. . . Чем больше размер типа, тем менее последовательный доступ к памяти осуществляется, а это весьма существенно для скорости работы. Поэтому реальное время возрастает чуть быстрее, нежели теоретическое. Кроме того, поразрядная сортировка уже по своей сути неинтересна для малых массивов. Каждый проход содержит минимум 256 итераций, поэтому при небольших n общее время выполнения (n+m) определяется константой m=256. Поведение неестественно, так как проходы выполняются полностью, вне зависимости от исходного состояния массива. Поразрядная сортировка является устойчивой.

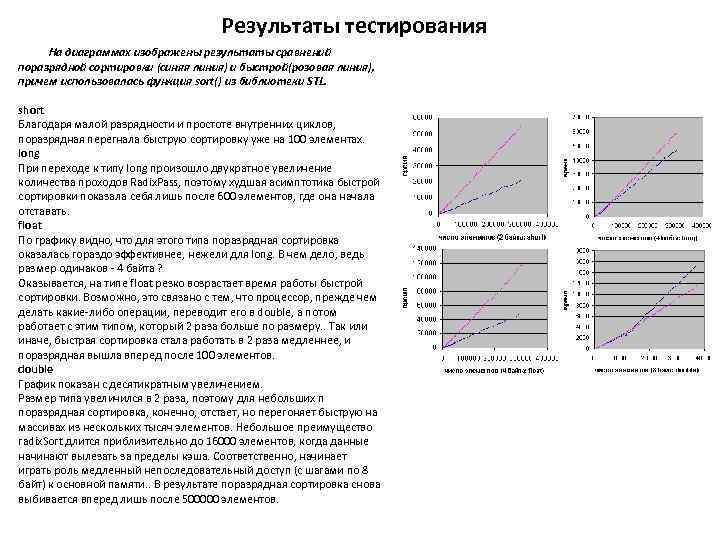Результаты тестирования На диаграммах изображены результаты сравнений поразрядной сортировки (синяя линия) и быстрой(розовая линия), причем использовалась функция sort() из библиотеки STL. short Благодаря малой разрядности и простоте внутренних циклов, поразрядная перегнала быструю сортировку уже на 100 элементах. long При переходе к типу long произошло двукратное увеличение количества проходов Radix. Pass, поэтому худшая асимптотика быстрой сортировки показала себя лишь после 600 элементов, где она начала отставать. float По графику видно, что для этого типа поразрядная сортировка оказалась гораздо эффективнее, нежели для long. В чем дело, ведь размер одинаков - 4 байта ? Оказывается, на типе float резко возрастает время работы быстрой сортировки. Возможно, это связано с тем, что процессор, прежде чем делать какие-либо операции, переводит его в double, а потом работает с этим типом, который 2 раза больше по размеру. . Так или иначе, быстрая сортировка стала работать в 2 раза медленнее, и поразрядная вышла вперед после 100 элементов. double График показан с десятикратным увеличением. Размер типа увеличился в 2 раза, поэтому для небольших n поразрядная сортировка, конечно, отстает, но перегоняет быструю на массивах из нескольких тысяч элементов. Небольшое преимущество radix. Sort длится приблизительно до 16000 элементов, когда данные начинают вылезать за пределы кэша. Соответственно, начинает играть роль медленный непоследовательный доступ (с шагами по 8 байт) к основной памяти. . В результате поразрядная сортировка снова выбивается вперед лишь после 500000 элементов.