Population Switching and Charge Sensing in Quantum Dots

Population Switching and Charge Sensing in Quantum Dots: A case for Quantum Phase Transitions PRL 104, 226805 (2010) Moshe Goldstein (Bar-Ilan Univ. , Israel), Richard Berkovits (Bar-Ilan Univ. , Israel), Yuval Gefen (Weizmann Inst. , Israel) Support: Adams, BINA, GIF, ISF, Minerva, SPP 1285

Outline • Introduction • Is population switching a QPT? • Coulomb gas analysis • A surprising twist: the effect of a charge sensor • Extensions; spin effects

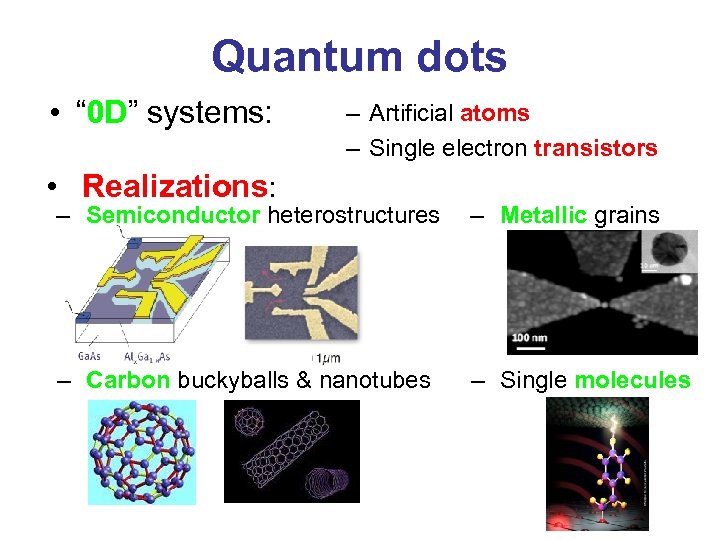Quantum dots • “ 0 D” systems: – Artificial atoms – Single electron transistors • Realizations: – Semiconductor heterostructures – Metallic grains – Carbon buckyballs & nanotubes – Single molecules

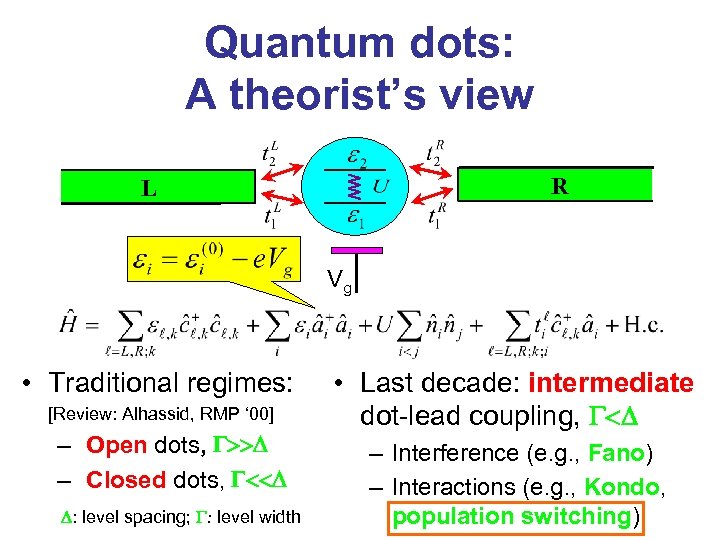Quantum dots: A theorist’s view R L Vg • Traditional regimes: [Review: Alhassid, RMP ‘ 00] – Open dots, G>>D – Closed dots, G<

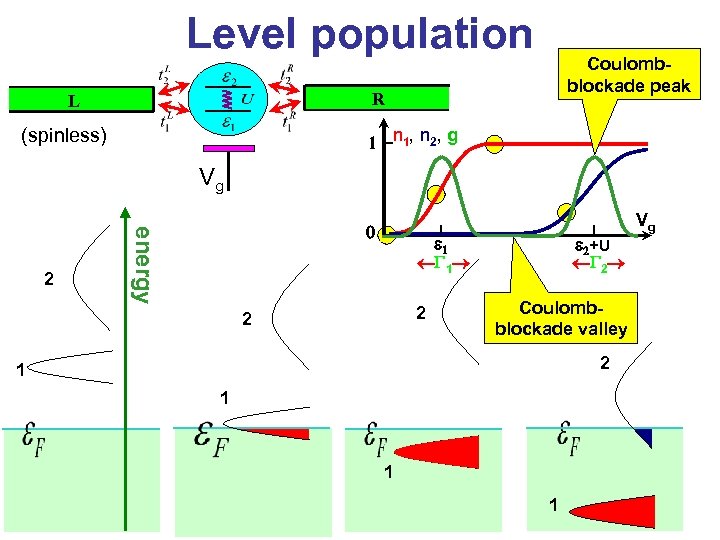Level population Coulombblockade peak R L (spinless) 1 n 1 , n 2 , g Vg energy 2 0 e 1 G 1 2 2 e 2+U G 2 Coulombblockade valley 2 1 1 Vg

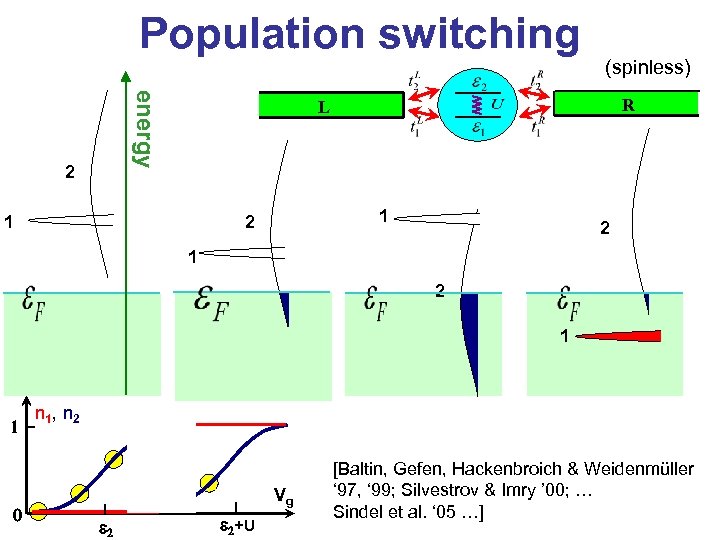Population switching energy 2 (spinless) R L 1 2 1 2 1 1 0 n 1 , n 2 Vg e 2+U [Baltin, Gefen, Hackenbroich & Weidenmüller ‘ 97, ‘ 99; Silvestrov & Imry ’ 00; … Sindel et al. ‘ 05 …]

Related phenomena • Charge sensing by QPC [widely used] L QD R QPC • Phase lapses [Heiblum group: Yacoby et al. ‘ 95; Shuster et al. ‘ 97; Avinun-Kalish et al. ‘ 05] – See also: MG, Berkovits, Gefen & Weidenmüller, PRB ‘ 09

Outline • Introduction • Is population switching a QPT? • Coulomb gas analysis • A surprising twist: the effect of a charge sensor • Extensions; spin effects

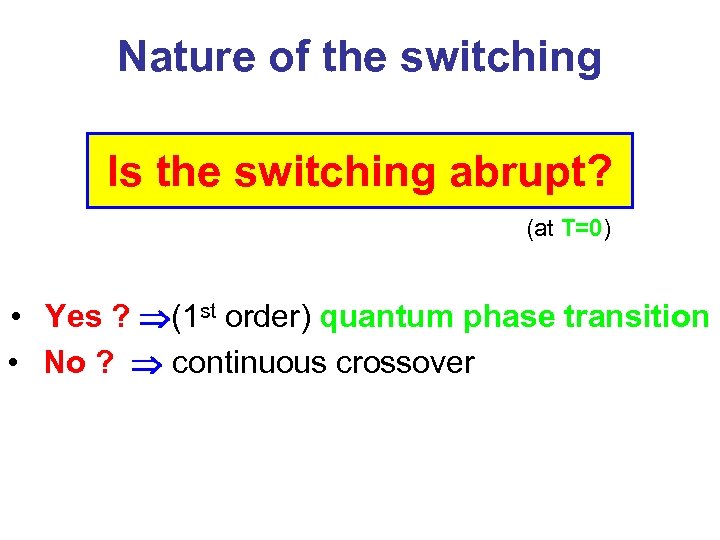Nature of the switching Is the switching abrupt? (at T=0) • Yes ? (1 st order) quantum phase transition • No ? continuous crossover

A limiting case • Decoupled narrow level: [Silvestrov & Imry ‘ 00] – Switching is abrupt – A single-particle problem: not a QPT free energy narrow level empty narrow level filled Vg • Many levels: [Marcus group: Johnson et al. ‘ 04] [Berkovits, von Oppen & Gefefn ‘ 05]

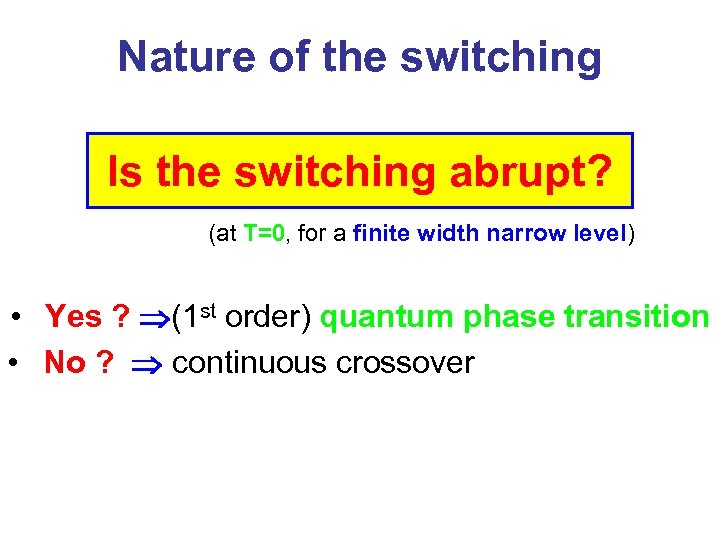Nature of the switching Is the switching abrupt? (at T=0, for a finite width narrow level) • Yes ? (1 st order) quantum phase transition • No ? continuous crossover

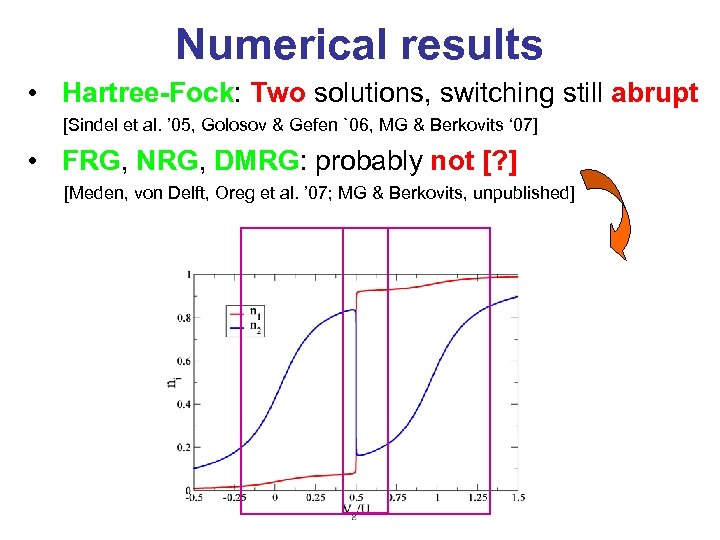Numerical results • Hartree-Fock: Two solutions, switching still abrupt [Sindel et al. ’ 05, Golosov & Gefen `06, MG & Berkovits ‘ 07] • FRG, NRG, DMRG: probably not [? ] [Meden, von Delft, Oreg et al. ’ 07; MG & Berkovits, unpublished]

Outline • Introduction • Is population switching a QPT? • Coulomb gas analysis • A surprising twist: the effect of a charge sensor • Extensions; spin effects

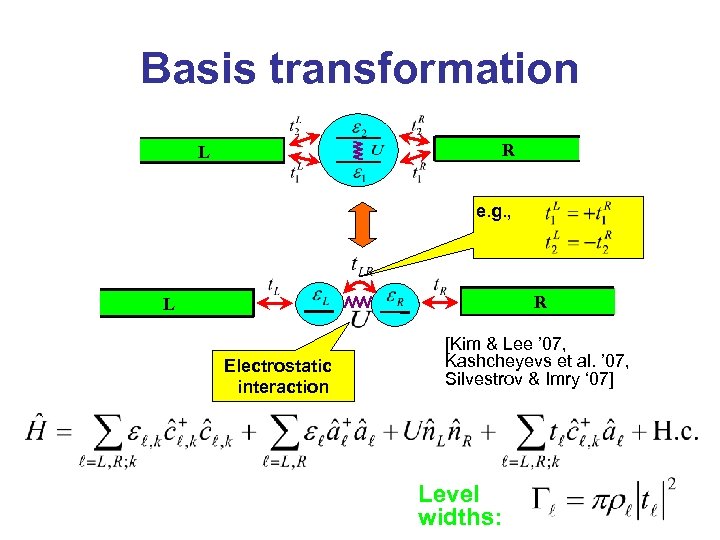Basis transformation R L e. g. , R L Electrostatic interaction [Kim & Lee ’ 07, Kashcheyevs et al. ’ 07, Silvestrov & Imry ‘ 07] Level widths:

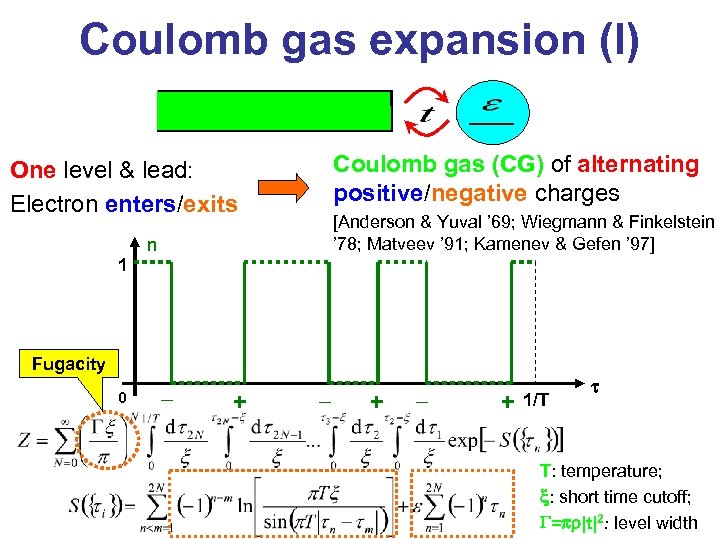Coulomb gas expansion (I) Coulomb gas (CG) of alternating positive/negative charges One level & lead: Electron enters/exits 1 [Anderson & Yuval ’ 69; Wiegmann & Finkelstein ’ 78; Matveev ’ 91; Kamenev & Gefen ’ 97] n Fugacity 0 – + – + 1/T t T: temperature; x: short time cutoff; G=pr|t|2: level width

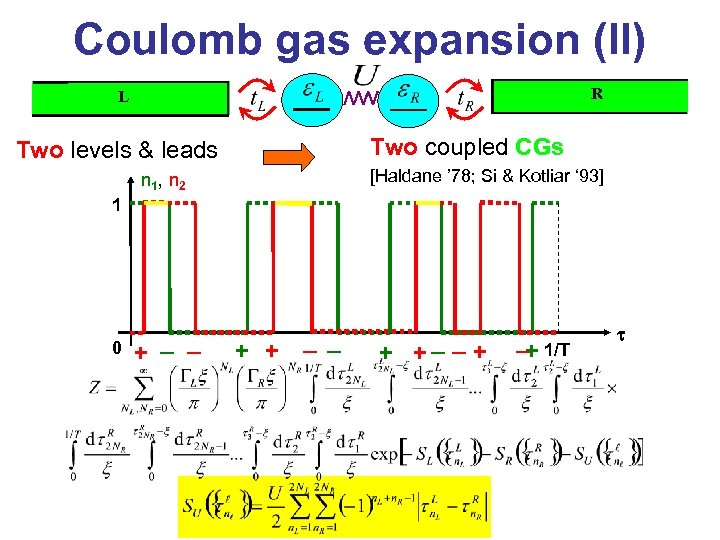Coulomb gas expansion (II) R L Two coupled CGs Two levels & leads [Haldane ’ 78; Si & Kotliar ‘ 93] n 1 , n 2 1 0 + – – + + –– + +– – + – 1/T + t

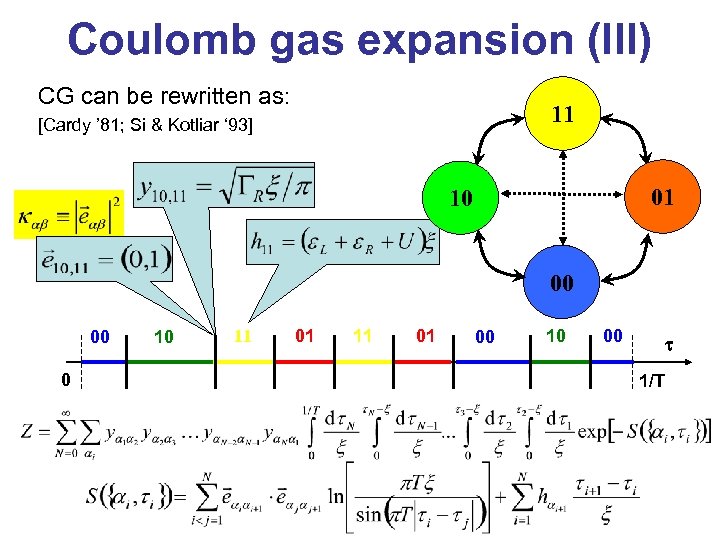Coulomb gas expansion (III) CG can be rewritten as: 11 [Cardy ’ 81; Si & Kotliar ‘ 93] 01 10 00 00 0 10 11 01 00 10 00 t 1/T

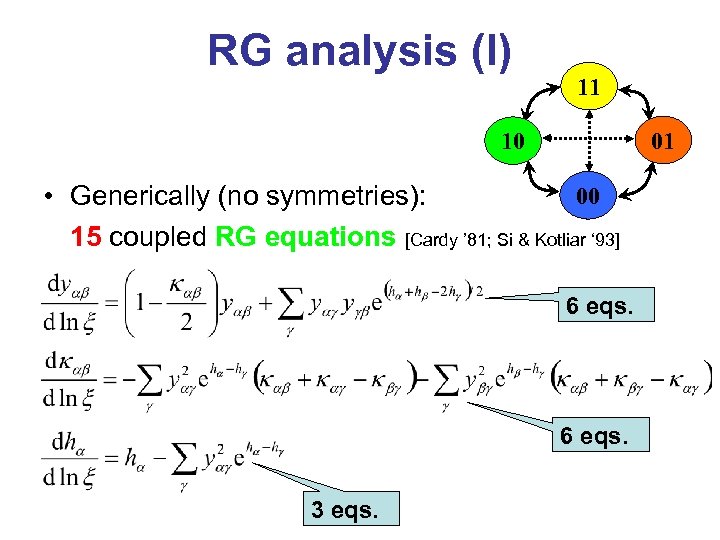RG analysis (I) 11 01 10 00 • Generically (no symmetries): 15 coupled RG equations [Cardy ’ 81; Si & Kotliar ‘ 93] 6 eqs. 3 eqs.

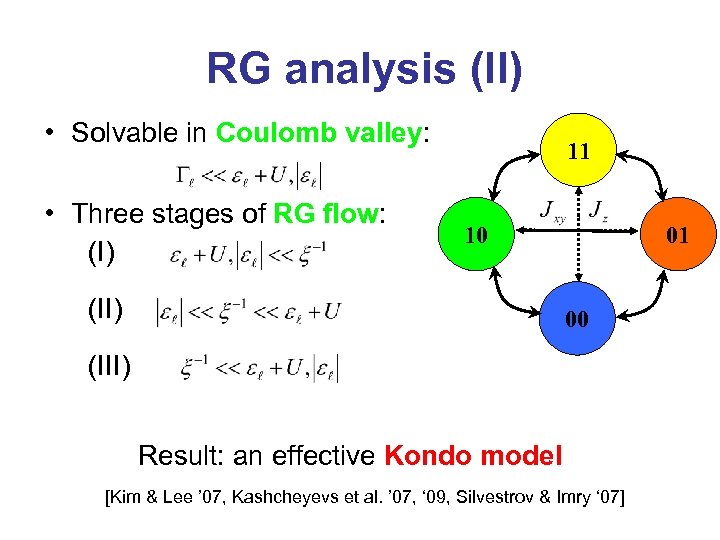RG analysis (II) • Solvable in Coulomb valley: • Three stages of RG flow: (I) 11 10 (II) 01 00 (III) Result: an effective Kondo model [Kim & Lee ’ 07, Kashcheyevs et al. ’ 07, ‘ 09, Silvestrov & Imry ‘ 07]

Digression: The Kondo problem • Realizations – Magnetic impurity – QD with odd electron number (spinful) L • Hamiltonian – J~t 2/U>0: exchange – hz: local magnetic field • Problem: divergences [Kondo ’ 64] – susceptibility: D: bandwidth – Similarly: resistance, specific heat …

Kondo: CG analysis • Anderson & Yuval [’ 69]: – Anisotropic model (Jz≠Jxy) – expand in Jxy: Coulomb gas of spin-flips Sz 1/2 0 – 1/2 1/T – + – + t

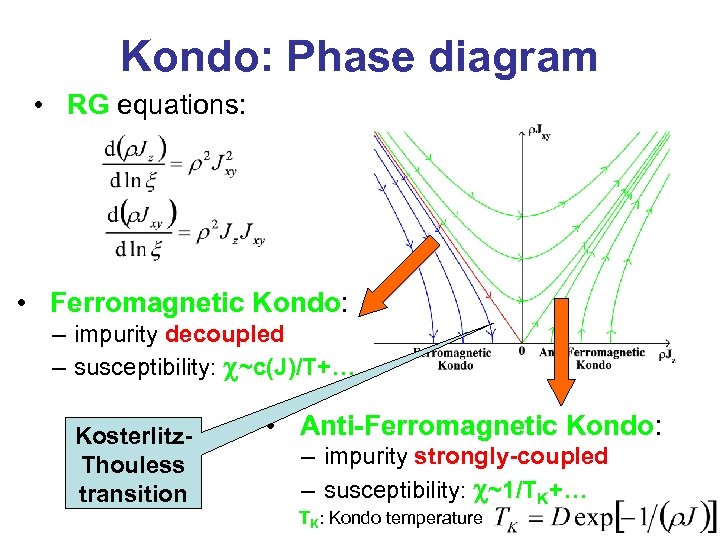Kondo: Phase diagram • RG equations: • Ferromagnetic Kondo: – impurity decoupled – susceptibility: c~c(J)/T+… Kosterlitz. Thouless transition • Anti-Ferromagnetic Kondo: – impurity strongly-coupled – susceptibility: c~1/TK+… TK: Kondo temperature

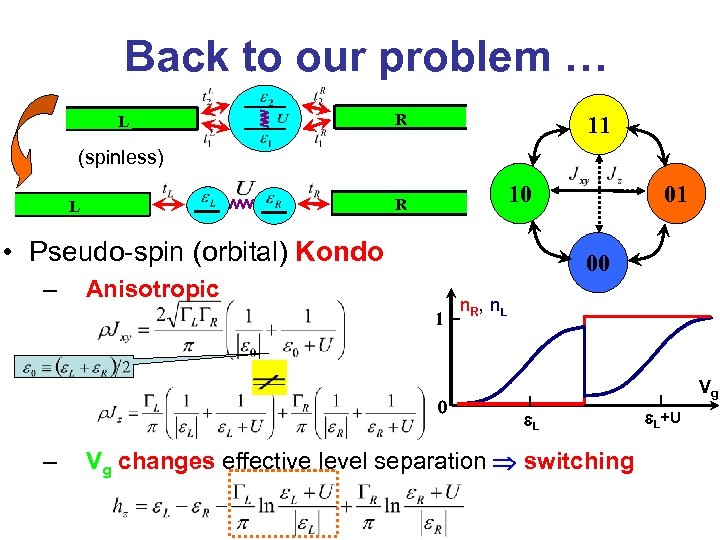Back to our problem … L R 11 (spinless) 10 R L • Pseudo-spin (orbital) Kondo – 00 Anisotropic 1 0 – 01 n. R , n. L Vg e. L Vg changes effective level separation switching e. L+U

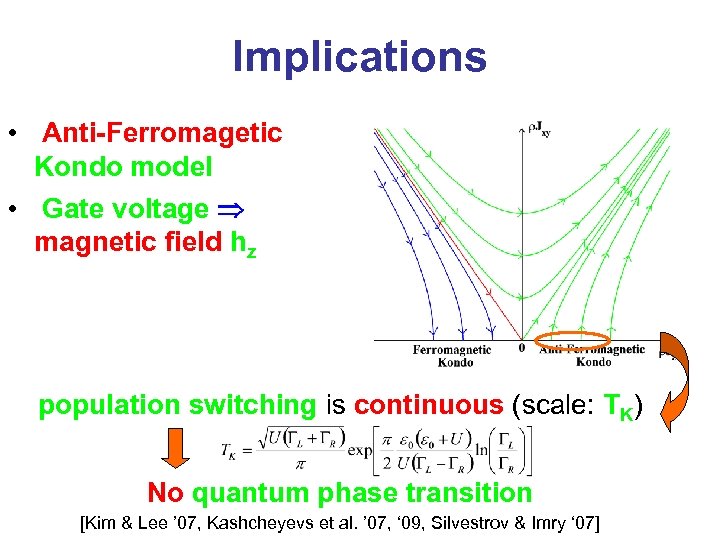Implications • Anti-Ferromagetic Kondo model • Gate voltage magnetic field hz population switching is continuous (scale: TK) No quantum phase transition [Kim & Lee ’ 07, Kashcheyevs et al. ’ 07, ‘ 09, Silvestrov & Imry ‘ 07]

What was gained? FDM Haldane on the Coulomb gas expansion: “Though an expression such as [the Coulomb gas expansion] … could be taken as the starting point of a scaling theory …, the more direct ‘poor man’s’ approach … proves simpler and more complete in practice. ” [J. Phys. C 11, 5015 (1978)]

Outline • Introduction • Is population switching a QPT? • Coulomb gas analysis • A surprising twist: the effect of a charge sensor • Extensions; spin effects

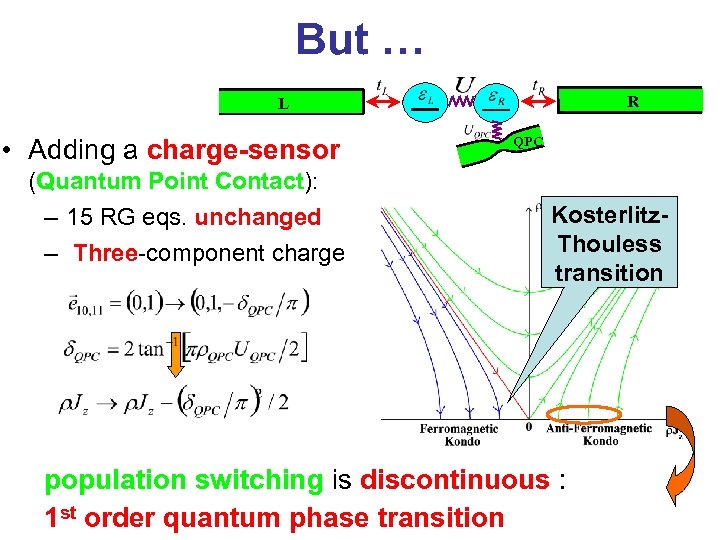But … R L • Adding a charge-sensor (Quantum Point Contact): – 15 RG eqs. unchanged – Three-component charge QPC Kosterlitz. Thouless transition population switching is discontinuous : 1 st order quantum phase transition

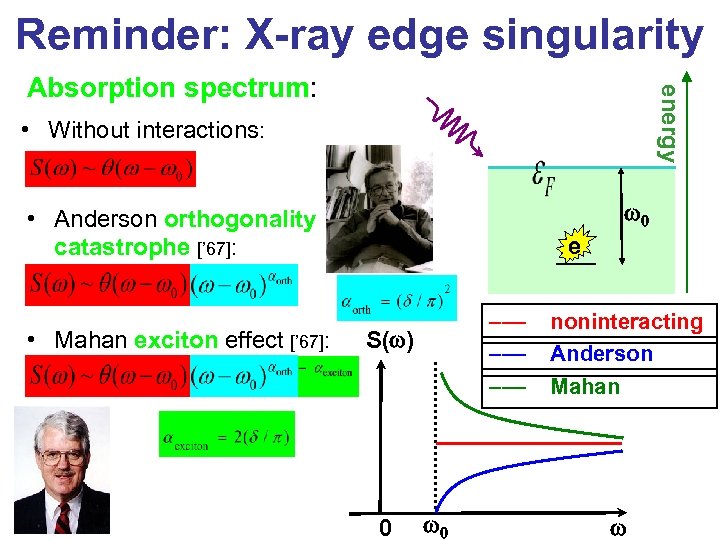Reminder: X-ray edge singularity energy Absorption spectrum: • Without interactions: w 0 • Anderson orthogonality catastrophe [’ 67]: • Mahan exciton effect [’ 67]: e ––– ––– S(w) 0 w 0 noninteracting Anderson Mahan w

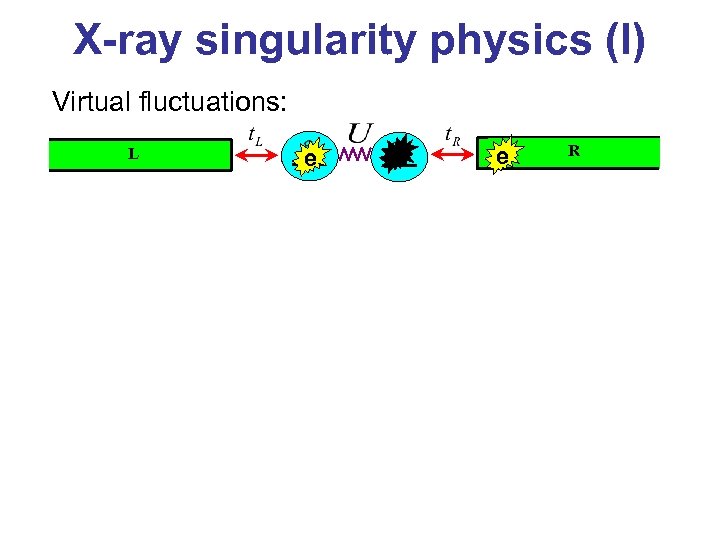X-ray singularity physics (I) Virtual fluctuations: L e e R

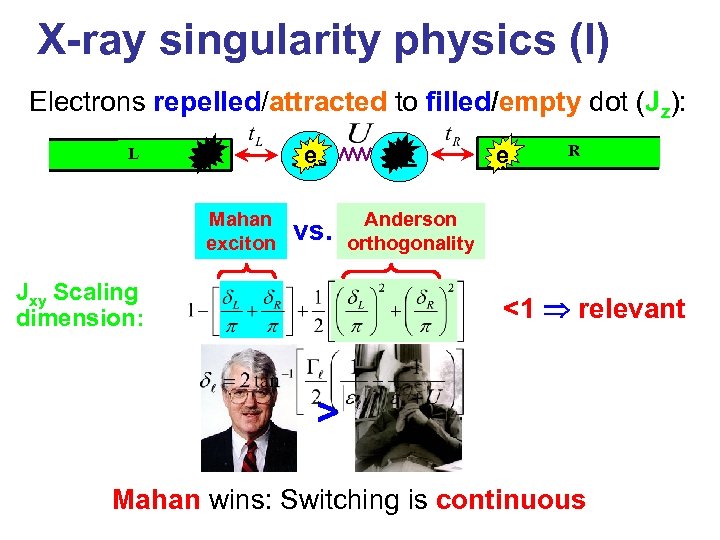X-ray singularity physics (I) Electrons repelled/attracted to filled/empty dot (Jz): e L Mahan exciton vs. Jxy Scaling dimension: e R Anderson orthogonality <1 relevant > Mahan wins: Switching is continuous

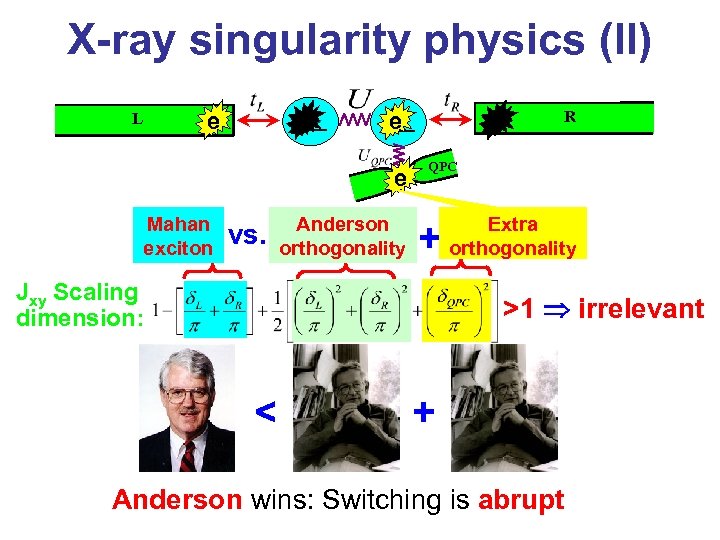X-ray singularity physics (II) e L e Mahan exciton R e vs. Anderson orthogonality QPC + Jxy Scaling dimension: Extra orthogonality >1 irrelevant < + Anderson wins: Switching is abrupt

A different perspective • Detector constantly measures the level population • Population dynamics suppressed: Quantum Zeno effect ! A sensor may induce a phase transition

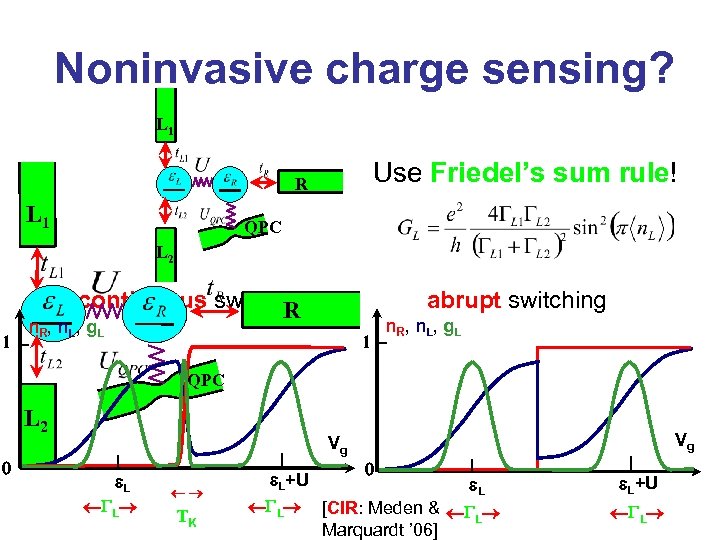Noninvasive charge sensing? L 1 Use Friedel’s sum rule! R L 1 QPC L 2 continuous switching R 1 abrupt switching n R , n L, g L 1 n R , n L, g L QPC L 2 0 Vg Vg e. L GL TK 0 e. L+U e. L GL [CIR: Meden & G L Marquardt ’ 06] e. L+U GL

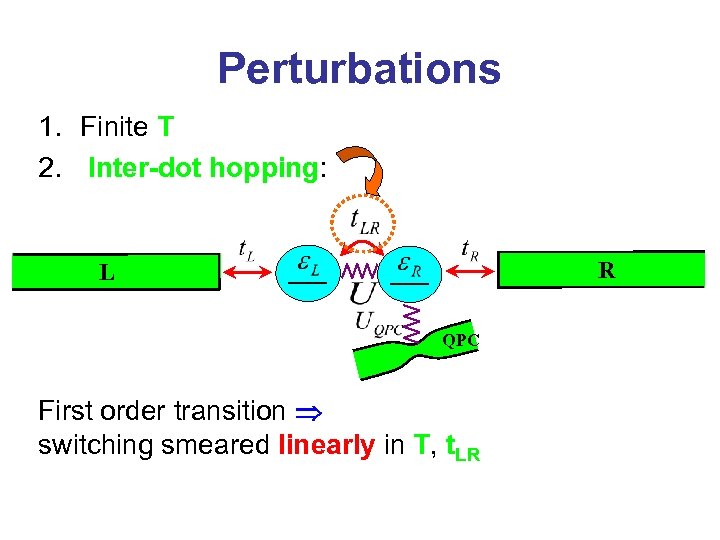Perturbations 1. Finite T 2. Inter-dot hopping: R L QPC First order transition switching smeared linearly in T, t. LR

Outline • Introduction • Is population switching a QPT? • Coulomb gas analysis • A surprising twist: the effect of a charge sensor • Extensions; spin effects

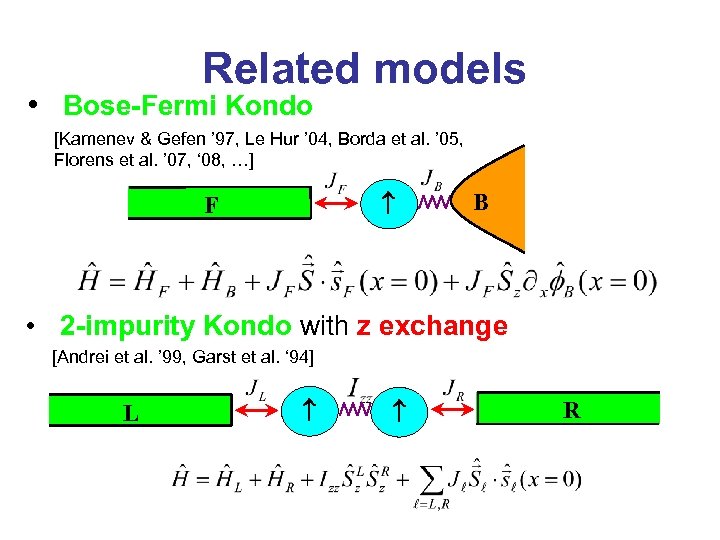Related models • Bose-Fermi Kondo [Kamenev & Gefen ’ 97, Le Hur ’ 04, Borda et al. ’ 05, Florens et al. ’ 07, ‘ 08, …] F B • 2 -impurity Kondo with z exchange [Andrei et al. ’ 99, Garst et al. ‘ 94] L R

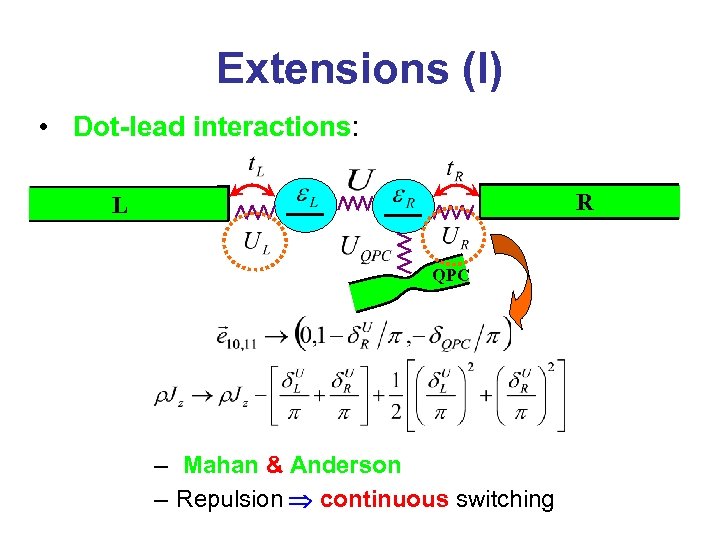Extensions (I) • Dot-lead interactions: R L QPC – Mahan & Anderson – Repulsion continuous switching

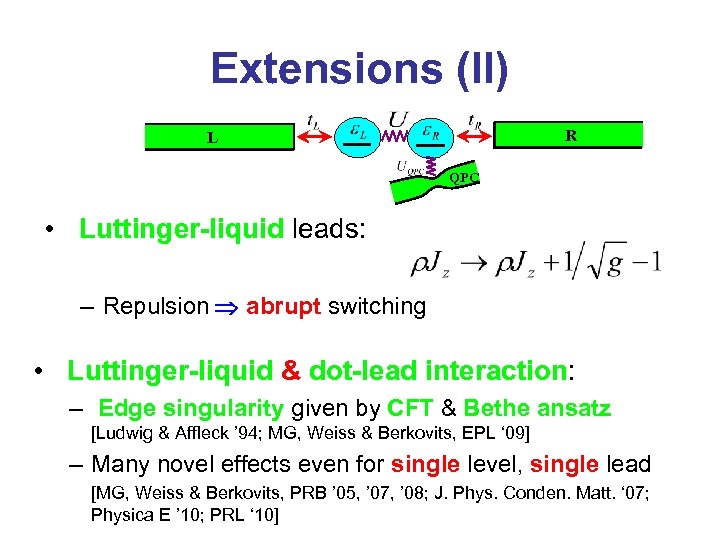Extensions (II) R L QPC • Luttinger-liquid leads: – Repulsion abrupt switching • Luttinger-liquid & dot-lead interaction: – Edge singularity given by CFT & Bethe ansatz [Ludwig & Affleck ’ 94; MG, Weiss & Berkovits, EPL ‘ 09] – Many novel effects even for single level, single lead [MG, Weiss & Berkovits, PRB ’ 05, ’ 07, ’ 08; J. Phys. Conden. Matt. ‘ 07; Physica E ’ 10; PRL ‘ 10]

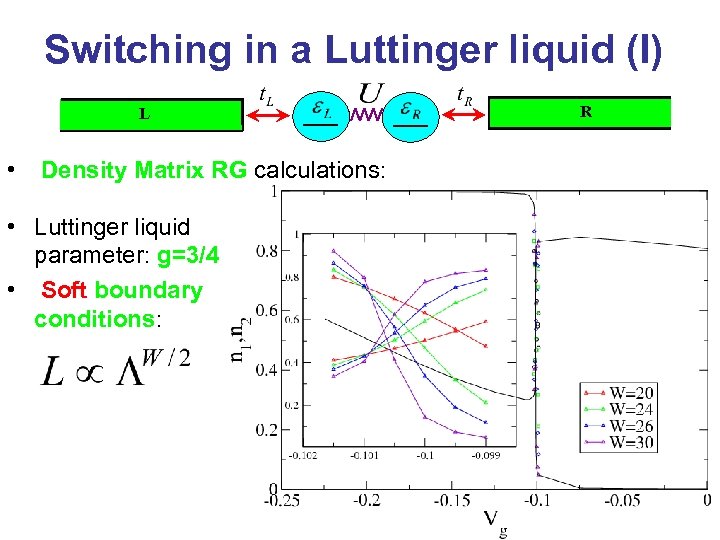Switching in a Luttinger liquid (I) L • Density Matrix RG calculations: • Luttinger liquid parameter: g=3/4 • Soft boundary conditions: R

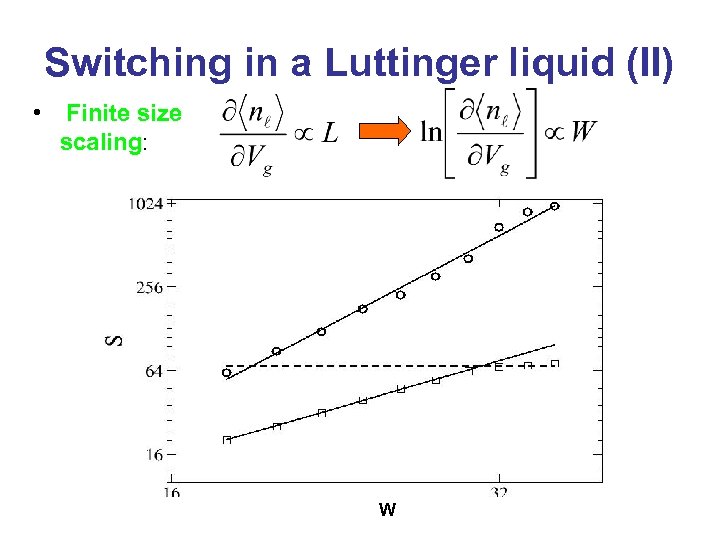Switching in a Luttinger liquid (II) • Finite size scaling: W

Conclusions • Population switching: – Usually: steep crossover, no quantum phase transition – Adding a charge sensor: 1 st order quantum phase transition • Laboratory for various effects: – Anderson orthogonality, Mahan exciton, quantum Zeno effect, entanglement entropy; – Kondo