ПОНЯТИЕ ВЕКТОРА Вектор отрезок для которого указано

ПОНЯТИЕ ВЕКТОРА Вектор – отрезок, для которого указано, какой из концов является началом, какой – концом. A B AB

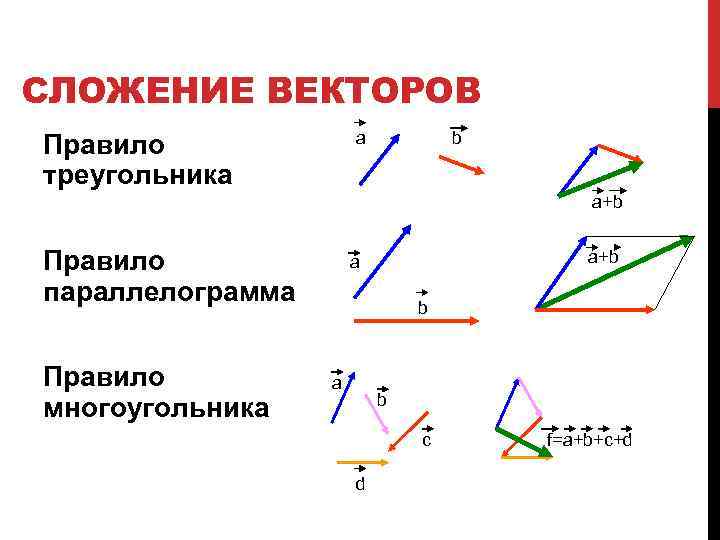СЛОЖЕНИЕ ВЕКТОРОВ a Правило треугольника b a+b Правило параллелограмма Правило многоугольника a+b a b c d f=a+b+c+d

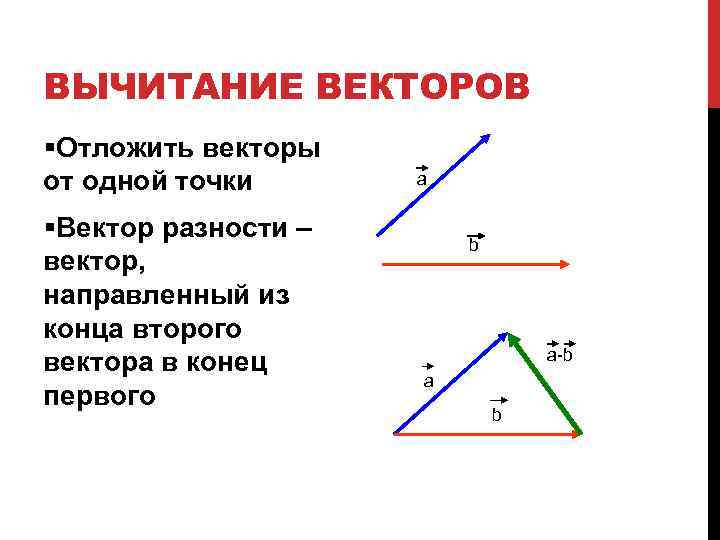ВЫЧИТАНИЕ ВЕКТОРОВ §Отложить векторы от одной точки §Вектор разности – вектор, направленный из конца второго вектора в конец первого а b a-b а b

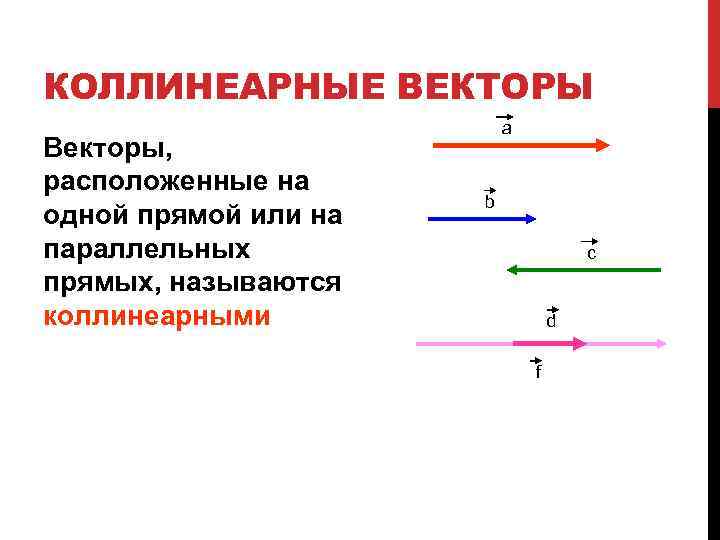КОЛЛИНЕАРНЫЕ ВЕКТОРЫ Векторы, расположенные на одной прямой или на параллельных прямых, называются коллинеарными a b c d f

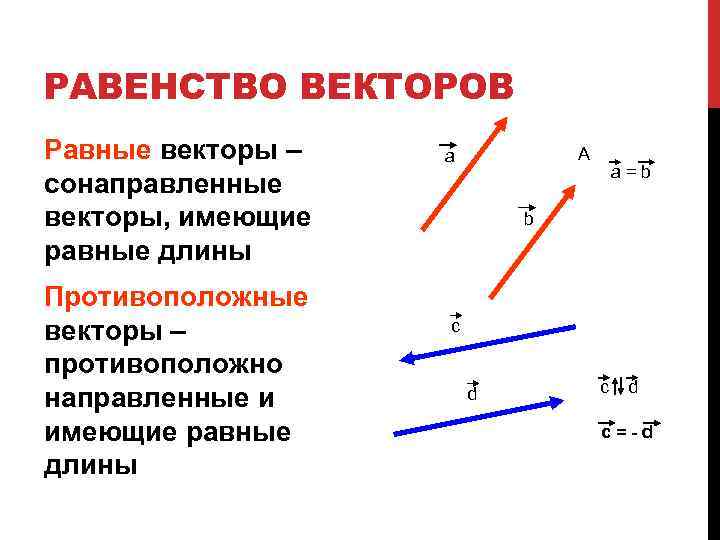РАВЕНСТВО ВЕКТОРОВ Равные векторы – сонаправленные векторы, имеющие равные длины Противоположные векторы – противоположно направленные и имеющие равные длины A a a=b b с d c=-d

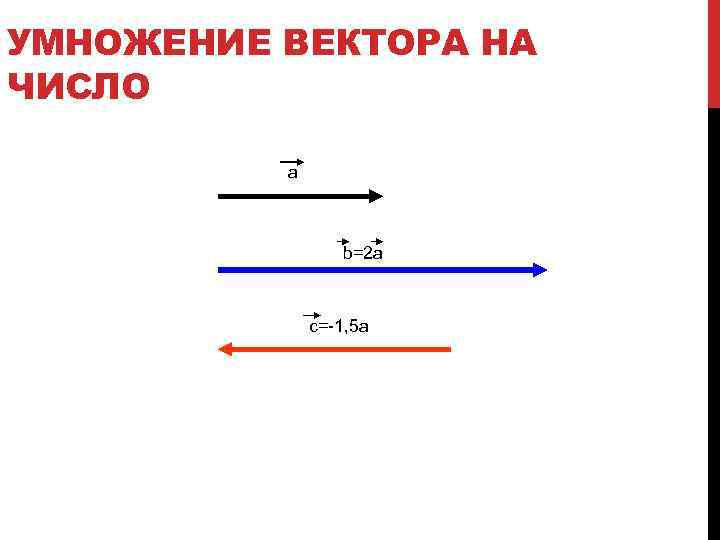УМНОЖЕНИЕ ВЕКТОРА НА ЧИСЛО a b=2 a c=-1, 5 a

ЗАКОНЫ СЛОЖЕНИЯ И УМНОЖЕНИЯ ВЕКТОРОВ Переместительный закон сложения a+b=b+a Сочетательный закон сложения (a + b) + c = a +(b + c) сочетательный закон умножения (x * a) * y =( x * y) * a Первый распределительный закон умножения ( a + b) * x = a * x + b * y Второй распределительный закон умножения (x+y)*a=x*a+y*b

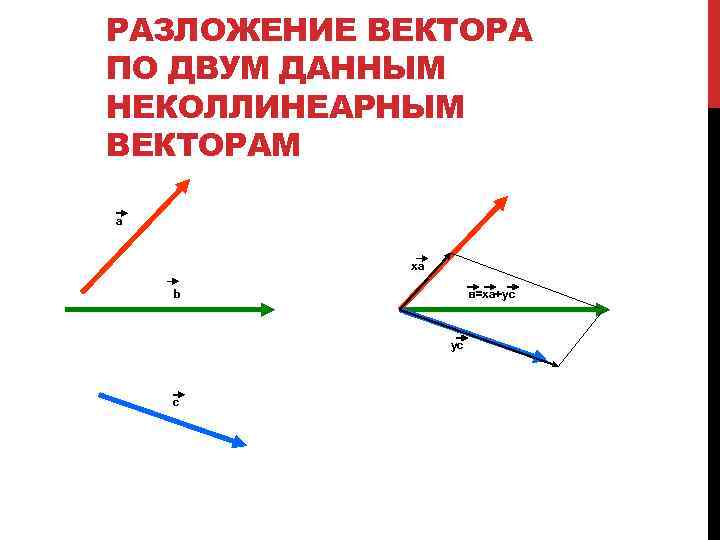РАЗЛОЖЕНИЕ ВЕКТОРА ПО ДВУМ ДАННЫМ НЕКОЛЛИНЕАРНЫМ ВЕКТОРАМ a xa b в=xa+yс yc c

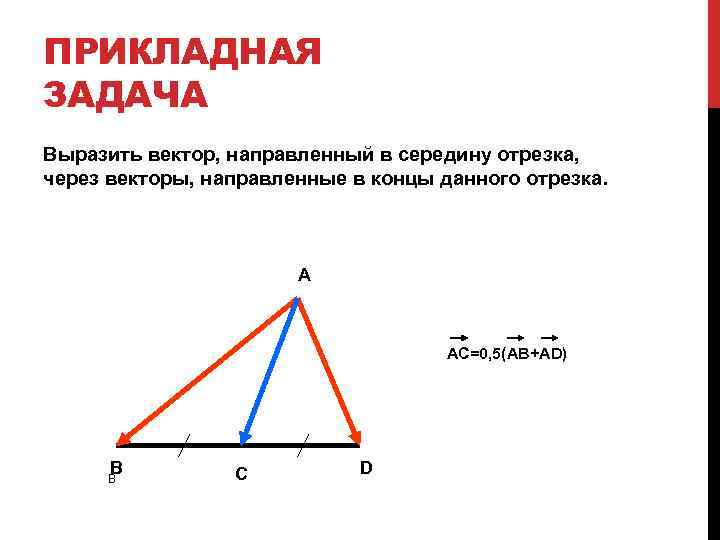ПРИКЛАДНАЯ ЗАДАЧА Выразить вектор, направленный в середину отрезка, через векторы, направленные в концы данного отрезка. A AC=0, 5(AB+AD) B B C D