Понятие синуса угла Выполнил Костромин Вячеслав 8 С

Понятие синуса угла Выполнил: Костромин Вячеслав 8 «С» класс МБОУ Лицей № 126

Цель: 1. Исследовать что такое синус угла. 2. История возникновения синуса угла. 3. Нахождение тригонометрических функций по единичной окружности. 4. Пример решения задачи.

Понятие синуса угла изучают в разделе «Тригонометрия» Этот раздел математики происходит от греческих слов «треугольник» и «мера» и означает измерение треугольников

Рассмотрим прямоугольный треугольник

Теперь увеличим стороны треугольника, а угол Х не изменим Таким образом можно менять длины сторон в прямоугольном треугольнике, но не менять угол х –и тогда отношения соответствующих сторон не изменятся.

А вот это уже очень важно! Отношения сторон в прямоугольном треугольнике не зависят от их длин при одном и том же угле. Поэтому они заслужили свои специальные названия. Sin x = a/c Синус угла х - это отношение противолежащего катета к гипотенузе.

Косинус угла х - это отношение прилежащего катета к гипотенузе Тангенс угла х - это отношение противолежащего катета к прилежащему Котангенс угла х - это отношение прилежащего катета к противолежащему Сos x = в/с tgx = а/в ctgx = в/а Термины синус и косинус относятся к углу. Угол здесь - главный

В древнем мире возникновение синуса связано с измерениями расстояния до недоступного предмета на земле, на небе, до звезд и строительным делом, измерение высоты пирамид, сооружений

Раньше люди считали, что Земля – это центр Вселенной и она неподвижна, а Солнце совершает за сутки один оборот вокруг Земли

Вавилонские жрецы, проводившие астрономические наблюдения, обнаружили, что в день равноденствия Солнце от восхода до заката описывает на небесном своде полуокружность, в которой видимый поперечник (диаметр) Солнца укладывается ровно 180 раз, 1° – след Солнца.

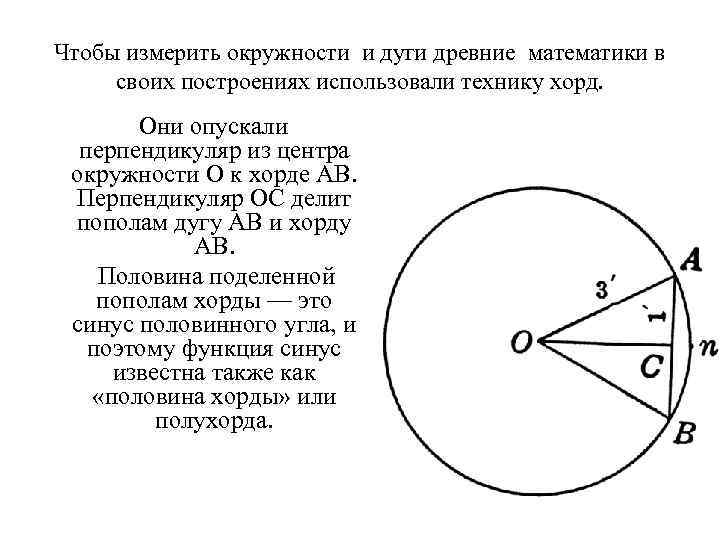Чтобы измерить окружности и дуги древние математики в своих построениях использовали технику хорд. Они опускали перпендикуляр из центра окружности О к хорде АВ. Перпендикуляр ОС делит пополам дугу АВ и хорду АВ. Половина поделенной пополам хорды — это синус половинного угла, и поэтому функция синус известна также как «половина хорды» или полухорда.

В IV-V веках появился уже специальный термин в астрономии у индийского учёного Ариабхаты в его сочинении — «Ариабхатия» (499), которое состоит из 4 частей в стихах. 1. Первая часть называется Дашагитика, в которой рассказывается о системе чисел и таблице синусов.

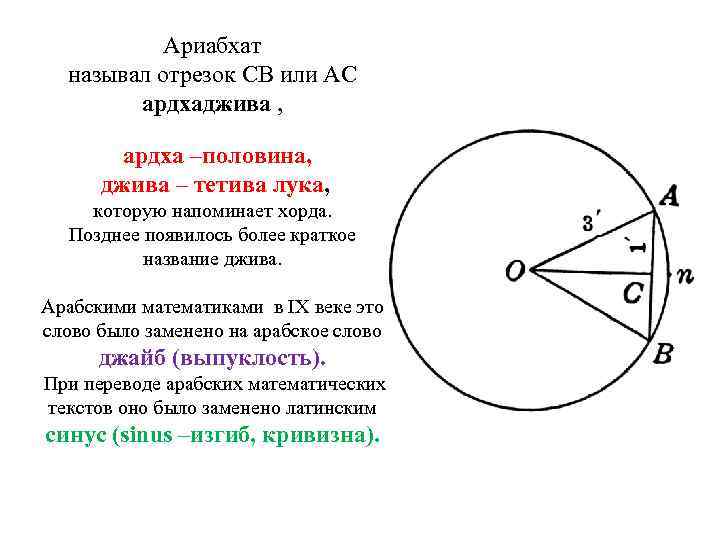Ариабхат называл отрезок CB или АС ардхаджива , ардха –половина, джива – тетива лука, которую напоминает хорда. Позднее появилось более краткое название джива. Арабскими математиками в IX веке это слово было заменено на арабское слово джайб (выпуклость). При переводе арабских математических текстов оно было заменено латинским синус (sinus –изгиб, кривизна).

Древнегреческий математик Гиппарх был первым, кто свёл в таблицы значения синусов и косинусов в зависимости от угла. Возможно Гиппарх взял идею такого деления у Гипсикла, который ранее разделил день на 360 частей, хотя такое деление дня могли предложить и вавилонские астрономы.

Известный среднеазиатский математик, по происхождению турок, Мухаммед ибн Муса ал-Хорезми в IX в. впервые в литературе на арабском языке составил таблицу синусов и ввел понятие «тангенс угла» .

Среднеазиатский математик и астроном Ал-Хабаш составил астрономические таблицы, в которые впервые ввел другие тригонометрические понятия: тангенс, котангенс, секанс и косеканс.

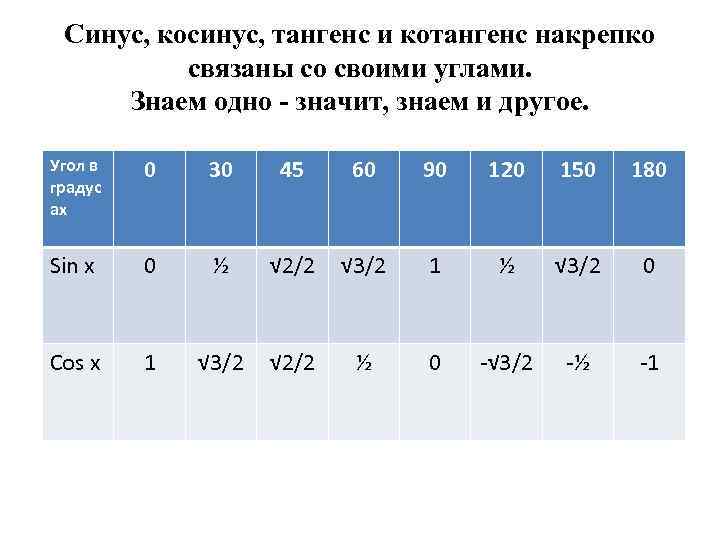Синус, косинус, тангенс и котангенс накрепко связаны со своими углами. Знаем одно - значит, знаем и другое. Угол в градус ах 0 30 45 60 90 120 150 180 Sin x 0 ½ √ 2/2 √ 3/2 1 ½ √ 3/2 0 Cos x 1 √ 3/2 √ 2/2 ½ 0 -√ 3/2 -½ -1

Узнать синус и косинус угла можно, пользуясь единичной окружностью

Пример решения задачи Всё. Больше никаких данных нет. Надо найти длину катета ВС. По клеточкам можно посчитать длину гипотенузы. 8 клеток. Ещё дан угол. Есть угол, значит, знаем все его тригонометрические функции. Нам известны гипотенуза, угол, а найти надо прилежащий к этому углу катет! косинус нужно в дело запускать! Просто пишем, по определению косинуса (отношение прилежащего катета к гипотенузе): Cos C = ВС/8 Угол С у нас 60 градусов, его косинус равен 1/2. Это знать надо, безо всяких таблиц! Стало быть: 1/2 = ВС/8 ВС = 4 Это и есть верный ответ.

Вывод

ТРИГОНОМЕТРИЯ Сферы • • • Астрономия Геодезия Картография Механика Оптика Акустика применения • • Строительство Архитектура Дизайн Навигация Медицина Музыка Спорт