 Понятие производной. Решение задачи Коши. Метод Эйлера - с пересчетом - усовершенствованный Метод Рунге-Кутта Метод Адамса Метод предиктор-корректор
Понятие производной. Решение задачи Коши. Метод Эйлера - с пересчетом - усовершенствованный Метод Рунге-Кутта Метод Адамса Метод предиктор-корректор
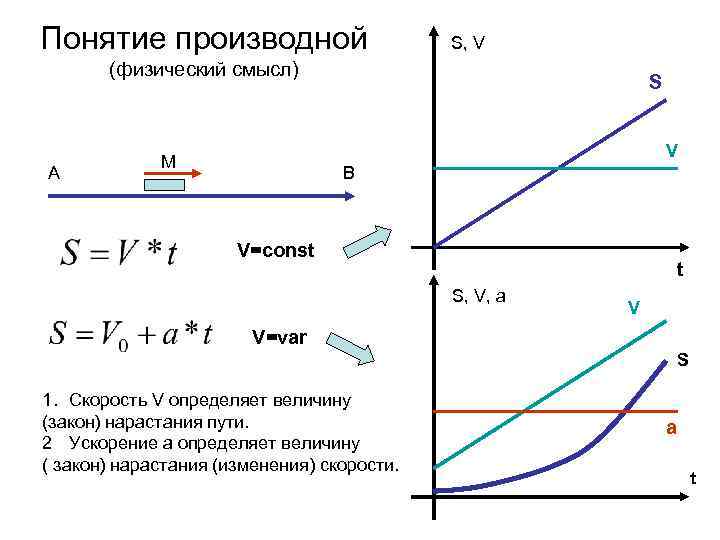 Понятие производной S, V (физический смысл) A S V M B V=const t S, V, а V V=var S 1. Скорость V определяет величину (закон) нарастания пути. 2 Ускорение а определяет величину ( закон) нарастания (изменения) скорости. a t
Понятие производной S, V (физический смысл) A S V M B V=const t S, V, а V V=var S 1. Скорость V определяет величину (закон) нарастания пути. 2 Ускорение а определяет величину ( закон) нарастания (изменения) скорости. a t
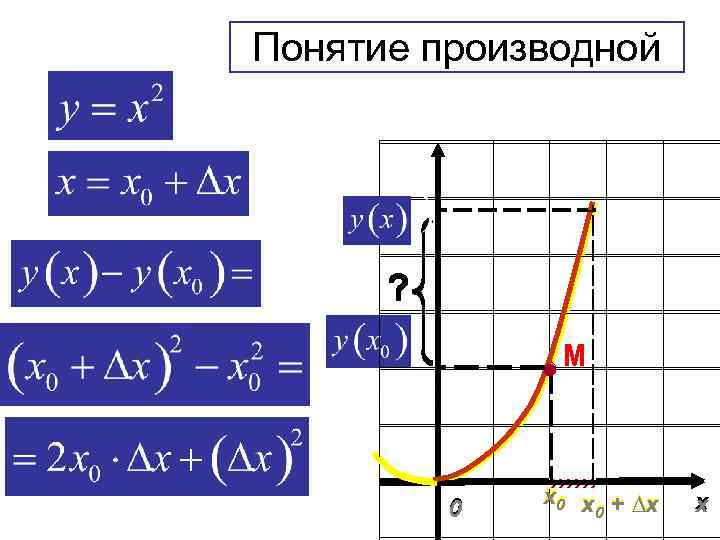 Понятие производной ? M 0 х0 х + ∆х 0 x
Понятие производной ? M 0 х0 х + ∆х 0 x
 Определение производной Производной функции y = f(x) в точке x 0 называется предел отношения приращения функции в точке x 0 к приращению аргумента при условии, что приращение аргумента стремится к нулю. Операция отыскания производной функции называется дифференцированием.
Определение производной Производной функции y = f(x) в точке x 0 называется предел отношения приращения функции в точке x 0 к приращению аргумента при условии, что приращение аргумента стремится к нулю. Операция отыскания производной функции называется дифференцированием.
 Дифференциальные уравнения
Дифференциальные уравнения
 дополнительные условия. Конец раздела
дополнительные условия. Конец раздела
 Задача Коши. Метод Эйлера Заменим производную на приращение h – шаг по х Конец раздела
Задача Коши. Метод Эйлера Заменим производную на приращение h – шаг по х Конец раздела
 Задача Коши. Метод Эйлера В результате получена табулированная функция, удовлетворяющая решению дифференциального уравнения. При необходимости получения функции в аналитическом виде она аппроксимируюется известными методами. Конец раздела
Задача Коши. Метод Эйлера В результате получена табулированная функция, удовлетворяющая решению дифференциального уравнения. При необходимости получения функции в аналитическом виде она аппроксимируюется известными методами. Конец раздела
 Задача Коши. Метод Эйлера с пересчетом Данная схема является неявной, поскольку левую части. входит в правую и
Задача Коши. Метод Эйлера с пересчетом Данная схема является неявной, поскольку левую части. входит в правую и
 Метод Эйлера с пересчетом имеет меньшую погрешность. Усовершенствованный метод Эйлера Остальные значения вычисляются аналогично Конец раздела
Метод Эйлера с пересчетом имеет меньшую погрешность. Усовершенствованный метод Эйлера Остальные значения вычисляются аналогично Конец раздела
 Задача Коши. Метод Рунге-Кутта Конец раздела
Задача Коши. Метод Рунге-Кутта Конец раздела
 Сравнительная оценка методов решения задачи Коши Решим задачу Коши следующими методами: 1. Метод Эйлера. 2. Метод Эйлера с пересчетом. 3. Усовершенствованный метод Эйлера. 4. Метод Рунге-Кутта. 5. Аналитическим методом.
Сравнительная оценка методов решения задачи Коши Решим задачу Коши следующими методами: 1. Метод Эйлера. 2. Метод Эйлера с пересчетом. 3. Усовершенствованный метод Эйлера. 4. Метод Рунге-Кутта. 5. Аналитическим методом.
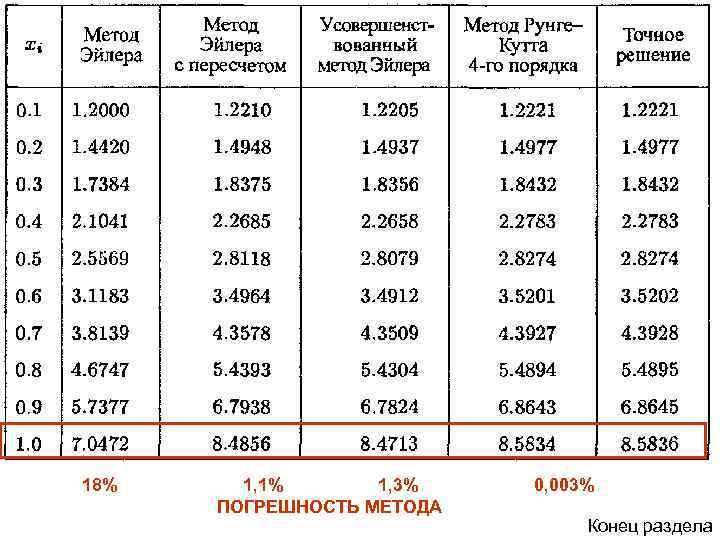 18% 1, 1% 1, 3% ПОГРЕШНОСТЬ МЕТОДА 0, 003% Конец раздела
18% 1, 1% 1, 3% ПОГРЕШНОСТЬ МЕТОДА 0, 003% Конец раздела
 Задача Коши. Метод Адамса более экономичен чем метод Рунге-Кутта при той же точности, но для вычисления значений Y 0, Y 1, Y 2, Y 3 нужно Воспользоваться другими методами, например Эйлера или Рунге-Кутта. Конец раздела
Задача Коши. Метод Адамса более экономичен чем метод Рунге-Кутта при той же точности, но для вычисления значений Y 0, Y 1, Y 2, Y 3 нужно Воспользоваться другими методами, например Эйлера или Рунге-Кутта. Конец раздела
 Метод прогноза и коррекции (метод предиктор-корректор) 1 этап - предикатор 2 этап - корректор Значения Y 0, Y 1, Y 2, Y 3 вычисляются другими методами Предиктор рассчитывается один раз, корректор вычисляется итерационно Конец раздела
Метод прогноза и коррекции (метод предиктор-корректор) 1 этап - предикатор 2 этап - корректор Значения Y 0, Y 1, Y 2, Y 3 вычисляются другими методами Предиктор рассчитывается один раз, корректор вычисляется итерационно Конец раздела