Понятие предиката Операции над предикатами

Понятие предиката. Операции над предикатами.

• Высказывания в алгебре логики рассматриваются как нераздельные целые и только с точки зрения их истинности или ложности. • Но алгебра логики, будучи важной частью логики оказывается недостаточной в анализе многих рассуждений.

• В связи с этим возникает необходимость в расширении логики высказываний. • В построении такой логической системы, средствами которой можно было бы исследовать структуру тех высказываний, которые в рамках логики высказываний рассматриваются как элементарные.

• Такой логической системой является логика предикатов, содержащая всю логику высказываний в качестве своей части.

• Логика предикатов, как и традиционная формальная логика, расчленяет элементарное высказывание на субъект (буквально подлежащее, хотя оно может играть роль дополнения) и предикат (буквально сказуемое, хотя оно может играть и роль определения).

• Субъект – это то, о чем что-то утверждается в высказывании; • Предикат- это то, что утверждается о субъекте. • Например: Число 5 есть нечетное число. Это высказывание утверждает, что 5 обладает свойством быть нечетным числом.

Если в рассмотренном примере заменить конкретное число 5 на любое другое число, то получим новое высказывание. Истинное или ложное. Число 7 есть нечетное число. (И) Число 8 есть нечетное число. (Л)

• Тогда, схема этого предложения имеет вид: • есть нечетное число. • Отсутствующий субъект можно заменить переменной (x, y, z…)

• Следовательно, возникает новое предложение: Число х есть простое число. • Это не высказывание, так как однозначно нельзя сказать истинно оно или ложно.

• Но в этом предложении сохранился предикат. • Это предложение можно назвать высказывательной формой. • При одних значениях (например, x=13, x=17) эта форма дает истинные высказывания, а при других значениях (например, x=8; x=12) эта форма дает ложные высказывания.

• Ясно, что эта высказывательная форма определяет функцию одной переменной x, определенной на множестве N, и принимающую значения из множества {И, Л} ( иначе {1, 0}).

• Определение • Одноместным предикатом P(x) называется произвольная функция переменного x, определённая на множестве X, и принимающая значения из множества {И, Л} (или {0, 1})

• Множество X, на котором определен предикат P(x), называется областью определения предиката P(x). • Множество всех элементов , при которых предикат принимает значения «истина» (1), называется множеством истинности предиката P(x). • Множество истинности будем обозначать T(P).

• Например: • - одноместный предикат, определен на множестве R (действительных чисел) • А множество истинности T(P) ={2, 3} • Предикат Q(x): sinx=0 определен на множестве R, а его множество истинности T(P) ={ }

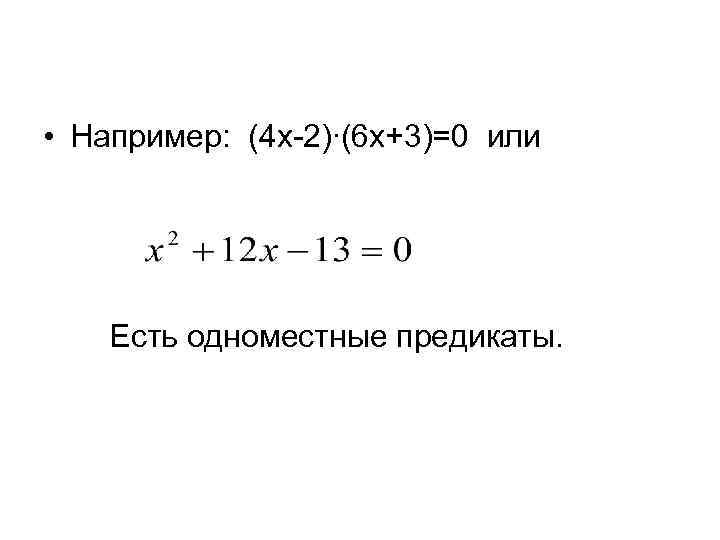• Например: (4 x-2)∙(6 x+3)=0 или Есть одноместные предикаты.

• Определение: Множеством истинности (Т) предиката называют совокупность значений переменных, для которых предикат принимает истинное значение. • А(х): (4 x-2)∙(6 x+3)=0, то • B(x): T(B) = {-13; 1} Т(A)={0, 5; -0, 5};

• Предикат F(x) – «Диагонали параллелограмма G взаимно перпендикулярны» определен на множестве всех параллелограммов. • T(F) - множество ромбов. • Замечание: из приведенных примеров видно, что одноместные предикаты выражают свойства предметов.

• Предикат P(x), определенный на множестве X, называется тождественно истинным, если его множество истинности совпадает с областью определения. T(P) =X. • Предикат P(x), определенный на множестве X, называется тождественно ложным, если его множество истинности является пустым множеством. • T(P) = Ø

• Естественным обобщением понятия одноместного предиката является понятие многоместного предиката, с помощью которого выражаются отношения между предметами. • Примером двуместного предиката является отношение «меньше» . • «x

• Предикат «x

• Примерами двуместных предикатов могут быть отношения: • S(x. y): x=y ; ( быть равным) • H(x, y): прямая х параллельна прямой y. (быть параллельным) • Совершенно аналогично вводится понятие трехместного предиката (функция трех переменных).

Логические операции над предикатами • Предикаты так же, как и высказывания, могут принимать два значения: «истина» (1) и «ложь» (0), поэтому к предикатам можно применить все операции логики высказываний, в результате чего из простых предикатов образуются сложные предикаты.

Конъюнкция предикатов • Пусть на некотором множестве X определены два предиката P(x) и Q(x) • Определение: • Конъюнкцией двух предикатов P(x) и Q(x) называется сложный предикат , который принимает значение «истина» при тех и только тех значениях переменной, при которых каждый из предикатов принимает значение «истина» , и значение «ложь» во всех остальных случаях.

• Теорема: Множество истинности конъюнкции двух предикатов есть пересечение множеств истинности простых предикатов, входящих в конъюнкцию. • Пусть Р(х) и Q(х) одноместные предикаты. • Т(P) -множество истинности предиката Р(х); • Т(Q)- множество истинности предиката Q(x).

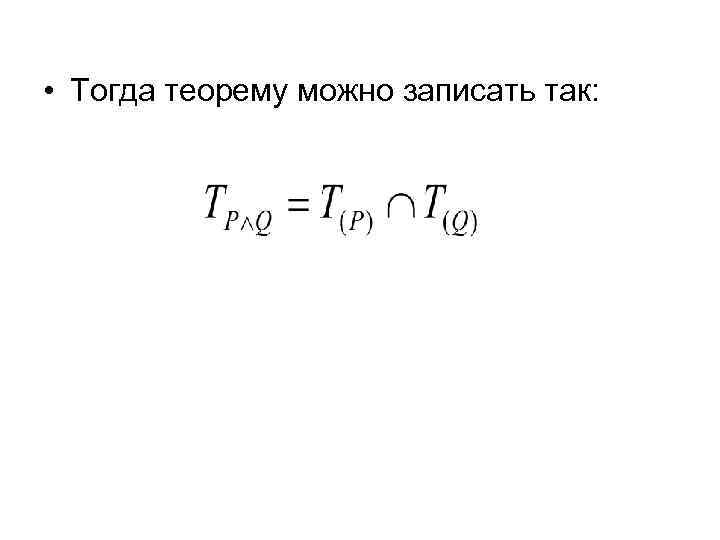• Тогда теорему можно записать так:

Доказательство • 1. Пусть a –произвольный элемент из области определения простых предикатов, Х –область определения предикатов.

• 2. Пусть a принадлежит множеству истинности конъюнкции, тогда Вывод: Из 1 и 2 следует справедливость утверждения. ч. т. д.

• Например: P(x): «х-четное число» • Q(x): «х- кратно 3» • Конъюнкция предикатов есть предикат «х – четное и х – кратно 3» . Этот предикат тождественен предикату «х- кратно 6» .

• Конъюнкцию предикатов можно наблюдать на таком примере. • Решить систему неравенств.

• Если предикат P(x) сложный, то • P(X): его можно разбить на простые предикаты. А(х): х-10<0 Ответ: (7; 10) и В(х): х-7>0

Дизъюнкция предикатов • Определение: Дизъюнкцией предикатов P(x) и Q(x) называется сложный предикат, который принимает значение «ложь» при всех тех и только тех значениях переменной из области определения, при которых каждый из предикатов принимает значение «ложь» , и принимает значение «истина» во всех остальных случаях.

• Теорема: Множеством истинности дизъюнкции предикатов является объединение множеств истинности простых предикатов, составляющих дизъюнкцию.

• Доказательство: • 1. Пусть произвольный элемент a принадлежит множеству истинности предикатов P(x) и Q(x).

• 2. Пусть произвольный элемент b принадлежит области определения предикатов, тогда Вывод: Из 1 и 2 следует справедливость утверждения. ч. т. д.

• Например. Самым распространенным примером дизъюнкции предикатов является уравнение. • (х-6)∙(х+5)=0 • х-6=0 или х+5=0 • Х=6 х=-5

• Если Р(х): (х-6)∙(х+5)=0, сложный предикат, то его можно разбить на простые предикаты. • А(х): х-6=0 и В(х): х+5=0 • Т(А) ={6} Т(В) ={-5}, тогда Ответ: Т(Р)={-5; 6}

Спасибо за внимание!