Скачать презентацию Понятие правильного многогранника Выпуклый многогранник называется правильным если
Презентация Microsoft Office PowerPoint.pptx
- Количество слайдов: 8
Понятие правильного многогранника: Выпуклый многогранник называется правильным, если все его грани – равные правильные многоугольники и в каждой его вершине сходится одно и то же число ребер
Утверждение: Не существует правильного многогранника, гранями которого являются правильные шестиугольники, семиугольники и вообще n-угольники при n≥ 6 Доказательство: Угол правильные шестиугольники при n≥ 6 не меньше 120◦. С другой стороны, при каждой вершине многогранника должно быть не менее трех плоских углов. Поэтому если бы существовал такой многогранник, то сумма плоских углов при каждой вершине была бы не меньше 360◦ (120◦ * 3◦). Но это не возможно так как сумма всех плоских углов при каждой вершине выпуклого многогранника меньше 360◦ Дополнение: По этой же прчине каждая вершина многогранника может быть вершиной либо трех, четырех или пяти равносторонних треугольников, либо трех квадратов, либо трех правильных пятиугольников.
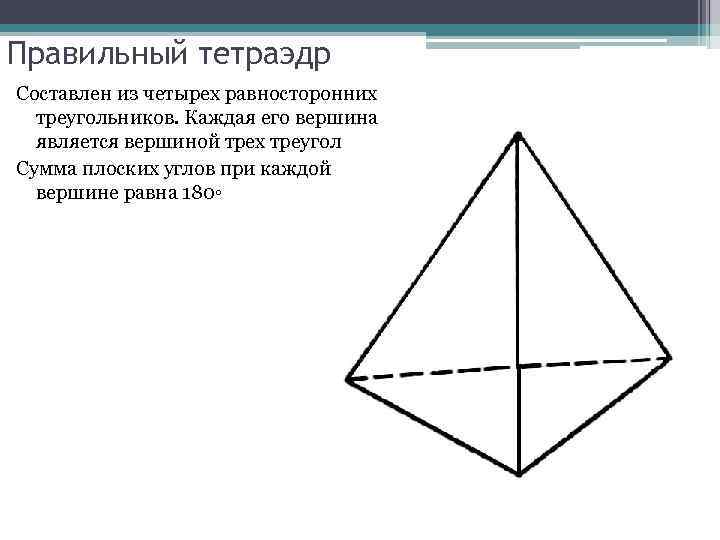Правильный тетраэдр Составлен из четырех равносторонних треугольников. Каждая его вершина является вершиной трех треугольников. Сумма плоских углов при каждой вершине равна 180◦
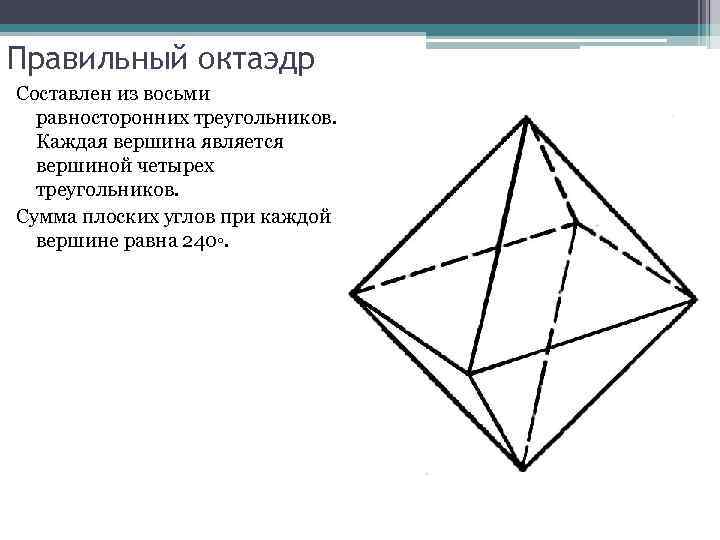Правильный октаэдр Составлен из восьми равносторонних треугольников. Каждая вершина является вершиной четырех треугольников. Сумма плоских углов при каждой вершине равна 240◦.
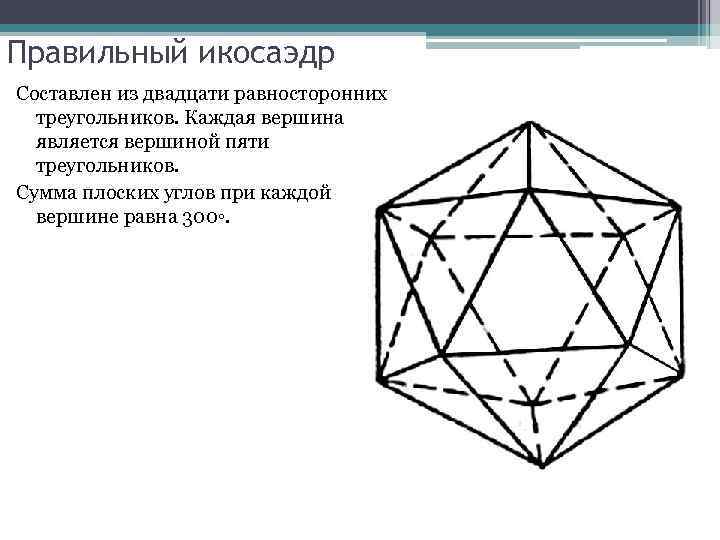Правильный икосаэдр Составлен из двадцати равносторонних треугольников. Каждая вершина является вершиной пяти треугольников. Сумма плоских углов при каждой вершине равна 300◦.
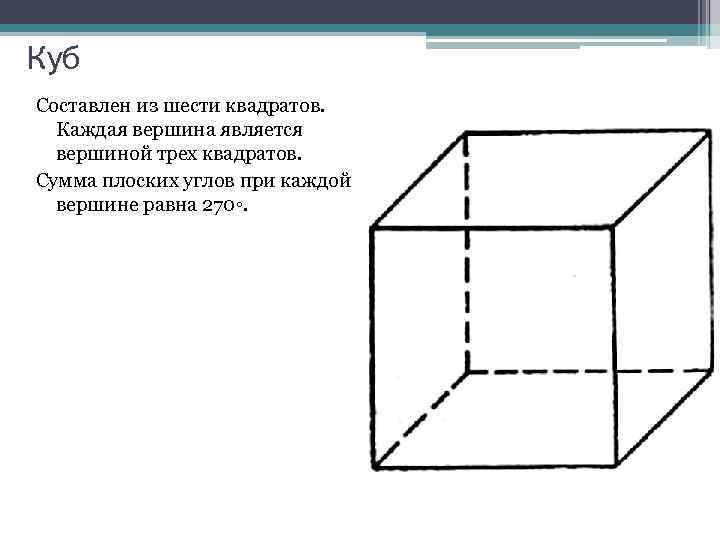Куб Составлен из шести квадратов. Каждая вершина является вершиной трех квадратов. Сумма плоских углов при каждой вершине равна 270◦.
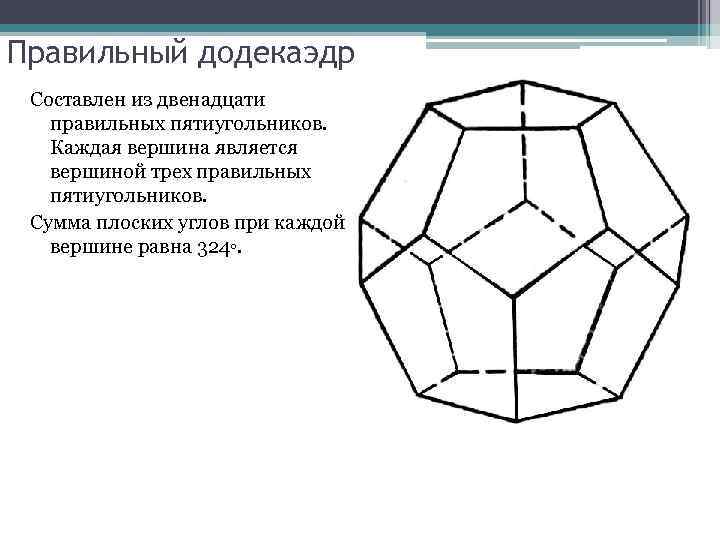Правильный додекаэдр Составлен из двенадцати правильных пятиугольников. Каждая вершина является вершиной трех правильных пятиугольников. Сумма плоских углов при каждой вершине равна 324◦.
